2021-2022学年北师大版九年级数学下册2.4二次函数的应用同步达标测评(Word版,附答案解析)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册2.4二次函数的应用同步达标测评(Word版,附答案解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 293.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-28 00:00:00 | ||
图片预览




文档简介
2021-2022学年北师大版九年级数学下册《2.4二次函数的应用》同步达标测评(附答案)
一.选择题(共10小题,满分30分)
1.从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的函数关系如图所示.下列结论:
①小球在空中经过的路程是40m;②小球运动的时间为6s;
③小球抛出3秒时,速度为0;④当t=1.5s时,小球的高度h=30m.
其中正确的是( )
A.①④ B.①② C.②③④ D.②④
2.如图,一位运动员推铅球,铅球行进高度y(m)与水平距离x(m)之间的关系是y=﹣,则此运动员把铅球推出多远( )
A.12m B.10m C.3m D.4m
3.烟花厂为成都春节特别设计制作了一种新型礼炮,这种礼炮的升空高度h(m)与飞行时间t(s)的关系式是.若这种礼炮在升空到最高点时引爆,则从点火升空到引爆需要的时间为( )
A.3s B.4s C.5s D.6s
4.图1是一个横断面为抛物线形状的拱桥,当水面在L时,拱顶(拱桥洞的最高点)离水面2m,水面宽为4m.如果水面宽度为6m,则水面下降( )
A.3.5m B.3m C.2.5m D.2m
5.已知某种礼炮的升空高度h(m)与飞行时间t(s)的关系式是h=﹣t2+20t+1.若此礼炮在升空到最高处时引爆,则引爆需要的时间为( )
A.3s B.4s C.5s D.6s
6.某景点的“喷水巨龙”口中C处的水流呈抛物线形,该水流喷出的高度y(m)与水平距离x(m)之间的关系如图所示,D为该水流的最高点,DA⊥OB,垂足为A.已知OC=OB=8m,OA=2m,则该水流距水平面的最大高度AD的长度为( )
A.9m B.10m C.11m D.12m
7.小强在一次训练中,掷出的实心球飞行高度y(米)与水平距离x(米)之间的关系大致满足二次函数y=﹣x2+x+,则小强此次成绩为( )
A.8米 B.10米 C.12米 D.14米
8.一人一盔安全守规,一人一带平安常在!某商店销售一批头盔,售价为每顶80元,每月可售出200顶.在“创建文明城市”期间,计划将头盔降价销售,经调查发现:每降价1元,每月可多售出20顶.已知头盔的进价为每顶50元,则该商店每月获得最大利润时,每顶头盔的售价为( )元.
A.60 B.65 C.70 D.75
9.我们定义一种新函数:形如y=|ax2+bx+c|(a≠0,b2﹣4ac>0)的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数y=|x2﹣2x﹣3|的图象(如图所示),并写出下列四个结论:其中正确结论的个数是( )
①图象具有对称性,对称轴是直线x=1;
②当﹣1<x<1或x>3时,函数值随x值的增大而增大;
③当x=﹣1或x=3时,函数的最小值是0;
④当x=1时,函数的最大值是4.
A.4 B.3 C.2 D.1
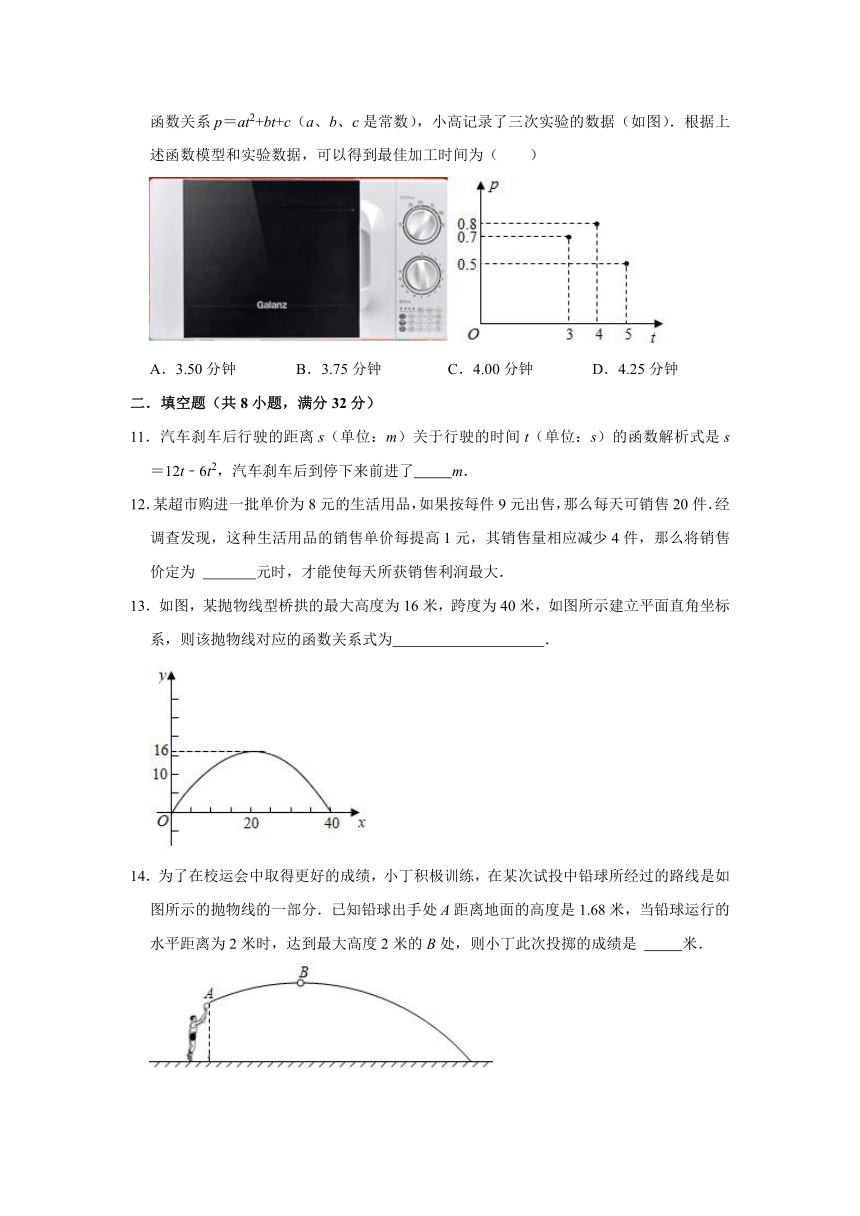
10.小高发现,用微波炉加工爆米花时,时间太短,一些颗粒没有充分爆开,时间太长,就糊了.如果将爆开且不糊的粒数的百分比称为“可食用率”.在特定条件下,可食用率p与加工时间t(单位:分钟)满足的函数关系p=at2+bt+c(a、b、c是常数),小高记录了三次实验的数据(如图).根据上述函数模型和实验数据,可以得到最佳加工时间为( )
A.3.50分钟 B.3.75分钟 C.4.00分钟 D.4.25分钟
二.填空题(共8小题,满分32分)
11.汽车刹车后行驶的距离s(单位:m)关于行驶的时间t(单位:s)的函数解析式是s=12t﹣6t2,汽车刹车后到停下来前进了 m.
12.某超市购进一批单价为8元的生活用品,如果按每件9元出售,那么每天可销售20件.经调查发现,这种生活用品的销售单价每提高1元,其销售量相应减少4件,那么将销售价定为 元时,才能使每天所获销售利润最大.
13.如图,某抛物线型桥拱的最大高度为16米,跨度为40米,如图所示建立平面直角坐标系,则该抛物线对应的函数关系式为 .
14.为了在校运会中取得更好的成绩,小丁积极训练,在某次试投中铅球所经过的路线是如图所示的抛物线的一部分.已知铅球出手处A距离地面的高度是1.68米,当铅球运行的水平距离为2米时,达到最大高度2米的B处,则小丁此次投掷的成绩是 米.
15.从喷水池喷头喷出的水珠,在空中形成一条抛物线,如图所示,在抛物线各个位置上,水珠的竖直高度y(单位:m)与它距离喷头的水平距离x(单位:m)之间满足函数关系式y=﹣2x2+4x+1,则喷出水珠的最大高度是 m.
16.在抛物线形拱桥中,以抛物线的对称轴为y轴,顶点为原点建立如图所示的平面直角坐标系,抛物线解析式为y=ax2,水面宽AB=6m,AB与y轴交于点C,OC=3m,当水面上升1m时,水面宽为 m.
17.退休的李老师借助自家15米的院墙和总长度为30米的围栏,在院墙外设计一个矩形花圃种植花草.为方便进出,他在如图所示的位置安装了一个1米宽的门,如果设和墙相邻的一边长为x米,花圃面积为y平方米,则y与x之间的函数关系式为 .
18.网络销售已经成为一种热门的销售方式,某网络平台为一服装厂直播代销一种服装(这里代销指厂家先免费提供货源,待货物销售后再进行结算,未售出的由厂家负责处理).销售中发现每件售价为250元时,日销售量为40件,当每件衣服每下降10元时,日销售量就会增加8件.已知每售出1件衣服,该平台需支付厂家和其它费用共100元.设每件衣服售价为x(元),该网络平台的日销售量为y(件).则下列结论正确的是 (填写所有正确结论序号).
①y与x的关系式是y=﹣x+240;②y与x的关系式是y=x﹣160;
③设每天的利润为W元,则W与x的关系式是W=﹣+320x﹣24000;
④按照厂家规定,每件售价不得低于210元,若该经销商想要每天获得最大利润,当每件售价定为210元时,每天利润最大,此时最大利润为7920元.
三.解答题(共6小题,满分58分)
19.一名男生推铅球,铅球的行进高度y(单位:m)与水平距离x(单位:m)之间的关系为,铅球行进路线如图.
(1)求出手点离地面的高度.
(2)求铅球推出的水平距离.
(3)通过计算说明铅球的行进高度能否达到4m.
20.某超市销售一款洗手液,这款洗手液成本价为每瓶16元,当销售单价定为每瓶20元时,每天可售出60瓶.市场调查反应:销售单价每上涨1元,则每天少售出5瓶.若设这款洗手液的销售单价上涨x元,每天的销售量利润为y元.
(1)每天的销售量为 瓶,每瓶洗手液的利润是 元;(用含x的代数式表示)
(2)若这款洗手液的日销售利润y达到300元,则销售单价应上涨多少元?
(3)当销售单价上涨多少元时,这款洗手液每天的销售利润y最大,最大利润为多少元?
21.某游乐场的圆形喷水池中心O有一雕塑OA,从A点向四周喷水,喷出的水柱为抛物线,且形状相同.如图,以水平方向为x轴,点O为原点建立直角坐标系,点A在y轴上,x轴上的点C,D为水柱的落水点,水柱所在抛物线(第一象限部分)的函数表达式为y=﹣(x﹣5)2+6.
(1)求雕塑高OA.
(2)求落水点C,D之间的距离.
(3)若需要在OD上的点E处竖立雕塑EF,OE=10m,EF=1.8m,EF⊥OD.问:顶部F是否会碰到水柱?请通过计算说明.
22.如图,有长为24米的篱笆,一面利用墙(墙的最大可用长度为10米)围成中间隔有一道篱笆的长方形花圃.设花圃AB边为x米,面积为y平方米.
(1)求y与x的函数关系式,并写出x的取值范围;
(2)如果要围成面积为45m2的花圃,求AB的长度;
(3)如果要使围成的花圃面积最大,求最大面积是多少m2.
23.如图,钢球从斜面顶端由静止开始沿斜面滚下,速度每秒增加1.5m.
(1)写出滚动的距离s(单位:m)关于滚动的时间t(单位:s)的函数解析式.(提示:本题中,距离=平均速度×时间t,=,其中,v0是开始时的速度,vt是t秒时的速度.)
(2)如果斜面的长是3m,钢球从斜面顶端滚到底端用多长时间?
24.设a、b是任意两个实数,用max{a,b}表示a、b两数中较大者,例如:max{﹣1,﹣1}=﹣1,max{1,2}=2,参照上面的材料,解答下列问题:
(1)max{5,2}= ,max{0,3}= ;
(2)若max{3x+1,﹣x+1}=﹣x+1,求x的取值范围;
(3)①求函数y=x2﹣2x﹣4与y=﹣x+2的图象的交点坐标.
②函数y=x2﹣2x﹣4的图象如图所示,请你在图中作出函数y=﹣x+2的图象,并根据图象直接写出max{﹣x+2,x2﹣2x﹣4}的最小值.
参考答案
一.选择题(共10小题,满分30分)
1.解:①由图象可知,小球在空中达到的最大高度为40m,则小球在空中经过的路程一定大于40m,故①错误;
②由图象可知,小球6s时落地,故小球运动的时间为6s,故②正确;
③小球抛出3秒时达到最高点,即速度为0,故③正确;
④设函数解析式为h=a(t﹣3)2+40,将(0,0)代入得:
0=a(0﹣3)2+40,
解得a=﹣,
∴函数解析式为h=﹣(t﹣3)2+40,
∴当t=1.5s时,h=﹣(1.5﹣3)2+40=30,
∴④正确.
综上,正确的有②③④.
故选:C.
2.解:令y=﹣=0
则:x2﹣8x﹣20=0
∴(x+2)(x﹣10)=0
∴x1=﹣2(舍),x2=10
由题意可知当x=10时,符合题意
故选:B.
3.解:∵礼炮在点火升空到最高点引爆,
∴t=﹣==6(s),
故选:D.
4.解:由题意可得,设抛物线解析式为:y=ax2,且抛物线过(2,﹣2)点,
故﹣2=a×22,
解得:a=﹣0.5,
∴抛物线解析式为:y=﹣0.5x2,
当水面宽度为6m时,即x=3时,
y=﹣0.5×9=﹣4,
∴水面下降﹣2﹣(﹣4)=2(m),
故选:D.
5.解:∵h=﹣t2+20t+1,
∴h=﹣(t﹣4)2+41,
∴顶点坐标为(4,41),
∴到达最高处的时间为4s.
故选:B.
6.解:根据题意,设抛物线解析式为y=a(x﹣2)2+k,
将点C(0,8)、B(8,0)代入,得:
,
解得,
∴抛物线解析式为y=﹣(x﹣2)2+9,
所以当x=2时,y=9,即AD=9m,
故选:A.
7.解:在y=﹣x2+x+中,当y=0时,﹣x2+x+=0,
解得x1=﹣2(舍去),x2=10,
即小强此次成绩为10米,
故选:B.
8.解:每顶头盔降价x元,利润为w元,
由题意可得,w=(80﹣x﹣50)(200+20x)=﹣20(x﹣10)2+8000,
∴当x=10时,w取得最大值,此时80﹣x=70,
即该商店每月获得最大利润时,每顶头盔的售价为70元,
故选:C.
9.解:观察图象可知,图象具有对称性,对称轴是直线x=﹣=1,故①正确;
令|x2﹣2x﹣3|=0可得x2﹣2x﹣3=0,
∴(x+1)(x﹣3)=0,
∴x1=﹣1,x2=3,
∴(﹣1,0)和(3,0)是函数图象与x轴的交点坐标,
又对称轴是直线x=1,
∴当﹣1<x<1或x>3时,函数值y随x值的增大而增大,故②正确;
由图象可知(﹣1,0)和(3,0)是函数图象的最低点,则当x=﹣1或x=3时,函数最小值是0,故③正确;
由图象可知,当x<﹣1时,函数值随x的减小而增大,当x>3时,函数值随x的增大而增大,均存在大于顶点坐标的函数值,
故当x=1时的函数值4并非最大值,故④错误.
综上,只有④错误.
故选:B.
10.解:由题意函数关系p=at2+bt+c(a,b,c是常数)经过点(3,0.7),(4,0.8),(5,0.5),
代入得:,
解得:,
∴p=﹣0.2t2+1.5t﹣2.2=﹣0.2(t﹣3.75)2+0.6125,
∴得到最佳加工时间为3.75分钟.
故选:B.
二.填空题(共8小题,满分32分)
11.解:∵s=12t﹣6t2=﹣6(t﹣1)2+6,
∴当t=1时,s取得最大值6,
即当t=1时,汽车刹车后行驶的距离s取得最大值6m,
∴汽车刹车后到停下来前进了6m,
故答案为:6.
12.解:设销售单价定为x元(x≥9),每天所获利润为y元,
则y=[20﹣4(x﹣9)] (x﹣8)
=﹣4x2+88x﹣448
=﹣4(x﹣11)2+36,
所以将销售定价定为11元时,才能使每天所获销售利润最大,
故答案为11.
13.解:由图象可知抛物线顶点坐标(20,16),经过(0,0),(40,0).
设抛物线的解析式为y=a(x﹣20)2+16,把(0,0)代入得到a=﹣,
∴抛物线的解析式为y=﹣(x﹣20)2+16,
即y=﹣x2+x,
故答案为:y=﹣x2+x.
14.解:建立坐标系,如图所示:
由题意得:A(0,1.68),B(2,2),点B为抛物线的顶点,
设抛物线的解析式为y=a(x﹣2)2+2,
把A(0,1.68)代入得:
4a+2=1.68,
解得a=﹣0.08,
∴y=﹣0.08(x﹣2)2+2,
令y=0,得﹣0.08(x﹣2)2+2=0,
解得x1=7,x2=﹣3(舍),
∴小丁此次投掷的成绩是7米.
故答案为:7.
15.解:∵y=﹣2x2+4x+1=﹣2(x﹣1)2+3,
∴当x=1时,y有最大值为3,
∴喷出水珠的最大高度是3m,
故答案为:3.
16.解:∵AB=6m,OC=3m,
∴点B坐标为(3,﹣3),
将B(3,﹣3)代入y=ax2得:
﹣3=a×32,
∴a=﹣,
∴y=﹣x2.
∴当水面上升1m时,即纵坐标y=﹣2时,有:
﹣2=﹣x2,
∴x2=6,
∴x1=﹣,x2=.
∴水面宽为:﹣(﹣)=2(m).
故答案为:2.
17.解:若和墙相邻的一边长为x米,则平行于墙的一边长为(30+1﹣2x)米,
依题意得:y=x(30+1﹣2x)=﹣2x2+31x.
又∵,
∴8≤x<15.5,
∴y与x之间的函数关系式为y=﹣2x2+31x(8≤x<15.5).
故答案为:y=﹣2x2+31x(8≤x<15.5).
18.解:∵y=40+=﹣x+240,
∴①正确,②错误;
∵w=(x﹣100)(﹣x+240)=﹣+320x﹣24000;
∴③正确;
∵w=(x﹣100)(﹣x+240)=﹣+320x﹣24000=﹣(x﹣200)2+8000,
a=﹣<0,每件售价不得低于210元,
所以当x=210时,每天利润最大是7920元,
∴④正确.
故答案为:①③④.
三.解答题(共6小题,满分58分)
19.解:(1)令x=0代入,
∴y=.
(2),
解得x1=10,x2=﹣2(舍去)
∴铅球推出的水平距离为10米.
(3)把y=4代入,得,
化简得x2﹣8x+28=0,方程无解,
∴铅球的行进高度不能达到4米.
20.解:(1)每天的销售量为(60﹣5x)瓶,每瓶洗手液的利润是(4+x)元;
故答案为:(60﹣5x);(4+x);
(2)根据题意得,(60﹣5x)(4+x)=300,
解得:x1=6,x2=2,
答:销售单价应上涨2元或6元;
(3)根据题意得,y=(60﹣5x)(4+x)=﹣5(x﹣12)(x+4)=﹣5(x﹣4)2+320,
答:当销售单价上涨4元时,这款洗手液每天的销售利润y最大,最大利润为320元.
21.解:(1)当x=0时,y=﹣(0﹣5)2+6=,
∴点A的坐标为(0,),
∴雕塑高m.
(2)当y=0时,﹣(x﹣5)2+6=0,
解得:x1=﹣1(舍去),x2=11,
∴点D的坐标为(11,0),
∴OD=11m.
∵从A点向四周喷水,喷出的水柱为抛物线,且形状相同,
∴OC=OD=11m,
∴CD=OC+OD=22m.
(3)当x=10时,y=﹣(10﹣5)2+6=,
∴点(10,)在抛物线y=﹣(x﹣5)2+6上.
又∵≈1.83>1.8,
∴顶部F不会碰到水柱.
22.解:(1)由题可知,花圃的宽AB为x米,则BC为(24﹣3x)米,
这时面积y=x(24﹣3x)=﹣3x2+24x,
∵0<24﹣3x≤10,
解得:≤x<8,
∴y=﹣3x2+24x(≤x<8);
(2)由条件﹣3x2+24x=45,
化简得x2﹣8x+15=0,
解得x1=5,x2=3,
∴x=3不合题意,舍去,
即AB的长度为5米;
(3)y=﹣3x2+24x=﹣3(x2﹣8x)=﹣3(x﹣4)2+48(≤x<8),
∵a=﹣3<0,开口向下,
∴当x=时,y有最大值48﹣3(﹣4)2=46,
故最大面积为46m2.
23.解:(1)由已知得vt=v0+at=0+1.5t=1.5t,
∴==,
∴s=t= t= t=t2,即s=t2;
(2)把s=3代入s=t2中,得t=2(t=﹣2舍去).
即钢球从斜面顶端滾到底端用2s.
答:钢球从斜面顶端滾到底端用2s.
24.解:(1)∵5>2,
∴max{5,2}=5,
∵3>0,
∴max{0,3}=3,
故答案为:5,3.
(2)∵max{3x+1,﹣x+1}=﹣x+1,
∴﹣x+1≥3x+1,
解得x≤0.
(3)①联立方程,
解得,,
∴函数y=x2﹣2x﹣4与y=﹣x+2的图象的交点坐标为(﹣2,4),(3,﹣1).
②如图,
∵图象交点为(﹣2,4),(3,﹣1),
∴当x≤﹣2时,x2﹣2x﹣4≥﹣x+2,且x2﹣2x﹣4≥4,
当﹣2<x<3时,﹣x+2>x2﹣2x﹣4,且﹣1<﹣x+2<4,
当x≥3时,x2﹣2x﹣4≥﹣x+2,且x2﹣2x﹣4≥﹣1,
综上所述,max{﹣x+2,x2﹣2x﹣4}的最小值为﹣1.
一.选择题(共10小题,满分30分)
1.从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的函数关系如图所示.下列结论:
①小球在空中经过的路程是40m;②小球运动的时间为6s;
③小球抛出3秒时,速度为0;④当t=1.5s时,小球的高度h=30m.
其中正确的是( )
A.①④ B.①② C.②③④ D.②④
2.如图,一位运动员推铅球,铅球行进高度y(m)与水平距离x(m)之间的关系是y=﹣,则此运动员把铅球推出多远( )
A.12m B.10m C.3m D.4m
3.烟花厂为成都春节特别设计制作了一种新型礼炮,这种礼炮的升空高度h(m)与飞行时间t(s)的关系式是.若这种礼炮在升空到最高点时引爆,则从点火升空到引爆需要的时间为( )
A.3s B.4s C.5s D.6s
4.图1是一个横断面为抛物线形状的拱桥,当水面在L时,拱顶(拱桥洞的最高点)离水面2m,水面宽为4m.如果水面宽度为6m,则水面下降( )
A.3.5m B.3m C.2.5m D.2m
5.已知某种礼炮的升空高度h(m)与飞行时间t(s)的关系式是h=﹣t2+20t+1.若此礼炮在升空到最高处时引爆,则引爆需要的时间为( )
A.3s B.4s C.5s D.6s
6.某景点的“喷水巨龙”口中C处的水流呈抛物线形,该水流喷出的高度y(m)与水平距离x(m)之间的关系如图所示,D为该水流的最高点,DA⊥OB,垂足为A.已知OC=OB=8m,OA=2m,则该水流距水平面的最大高度AD的长度为( )
A.9m B.10m C.11m D.12m
7.小强在一次训练中,掷出的实心球飞行高度y(米)与水平距离x(米)之间的关系大致满足二次函数y=﹣x2+x+,则小强此次成绩为( )
A.8米 B.10米 C.12米 D.14米
8.一人一盔安全守规,一人一带平安常在!某商店销售一批头盔,售价为每顶80元,每月可售出200顶.在“创建文明城市”期间,计划将头盔降价销售,经调查发现:每降价1元,每月可多售出20顶.已知头盔的进价为每顶50元,则该商店每月获得最大利润时,每顶头盔的售价为( )元.
A.60 B.65 C.70 D.75
9.我们定义一种新函数:形如y=|ax2+bx+c|(a≠0,b2﹣4ac>0)的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数y=|x2﹣2x﹣3|的图象(如图所示),并写出下列四个结论:其中正确结论的个数是( )
①图象具有对称性,对称轴是直线x=1;
②当﹣1<x<1或x>3时,函数值随x值的增大而增大;
③当x=﹣1或x=3时,函数的最小值是0;
④当x=1时,函数的最大值是4.
A.4 B.3 C.2 D.1
10.小高发现,用微波炉加工爆米花时,时间太短,一些颗粒没有充分爆开,时间太长,就糊了.如果将爆开且不糊的粒数的百分比称为“可食用率”.在特定条件下,可食用率p与加工时间t(单位:分钟)满足的函数关系p=at2+bt+c(a、b、c是常数),小高记录了三次实验的数据(如图).根据上述函数模型和实验数据,可以得到最佳加工时间为( )
A.3.50分钟 B.3.75分钟 C.4.00分钟 D.4.25分钟
二.填空题(共8小题,满分32分)
11.汽车刹车后行驶的距离s(单位:m)关于行驶的时间t(单位:s)的函数解析式是s=12t﹣6t2,汽车刹车后到停下来前进了 m.
12.某超市购进一批单价为8元的生活用品,如果按每件9元出售,那么每天可销售20件.经调查发现,这种生活用品的销售单价每提高1元,其销售量相应减少4件,那么将销售价定为 元时,才能使每天所获销售利润最大.
13.如图,某抛物线型桥拱的最大高度为16米,跨度为40米,如图所示建立平面直角坐标系,则该抛物线对应的函数关系式为 .
14.为了在校运会中取得更好的成绩,小丁积极训练,在某次试投中铅球所经过的路线是如图所示的抛物线的一部分.已知铅球出手处A距离地面的高度是1.68米,当铅球运行的水平距离为2米时,达到最大高度2米的B处,则小丁此次投掷的成绩是 米.
15.从喷水池喷头喷出的水珠,在空中形成一条抛物线,如图所示,在抛物线各个位置上,水珠的竖直高度y(单位:m)与它距离喷头的水平距离x(单位:m)之间满足函数关系式y=﹣2x2+4x+1,则喷出水珠的最大高度是 m.
16.在抛物线形拱桥中,以抛物线的对称轴为y轴,顶点为原点建立如图所示的平面直角坐标系,抛物线解析式为y=ax2,水面宽AB=6m,AB与y轴交于点C,OC=3m,当水面上升1m时,水面宽为 m.
17.退休的李老师借助自家15米的院墙和总长度为30米的围栏,在院墙外设计一个矩形花圃种植花草.为方便进出,他在如图所示的位置安装了一个1米宽的门,如果设和墙相邻的一边长为x米,花圃面积为y平方米,则y与x之间的函数关系式为 .
18.网络销售已经成为一种热门的销售方式,某网络平台为一服装厂直播代销一种服装(这里代销指厂家先免费提供货源,待货物销售后再进行结算,未售出的由厂家负责处理).销售中发现每件售价为250元时,日销售量为40件,当每件衣服每下降10元时,日销售量就会增加8件.已知每售出1件衣服,该平台需支付厂家和其它费用共100元.设每件衣服售价为x(元),该网络平台的日销售量为y(件).则下列结论正确的是 (填写所有正确结论序号).
①y与x的关系式是y=﹣x+240;②y与x的关系式是y=x﹣160;
③设每天的利润为W元,则W与x的关系式是W=﹣+320x﹣24000;
④按照厂家规定,每件售价不得低于210元,若该经销商想要每天获得最大利润,当每件售价定为210元时,每天利润最大,此时最大利润为7920元.
三.解答题(共6小题,满分58分)
19.一名男生推铅球,铅球的行进高度y(单位:m)与水平距离x(单位:m)之间的关系为,铅球行进路线如图.
(1)求出手点离地面的高度.
(2)求铅球推出的水平距离.
(3)通过计算说明铅球的行进高度能否达到4m.
20.某超市销售一款洗手液,这款洗手液成本价为每瓶16元,当销售单价定为每瓶20元时,每天可售出60瓶.市场调查反应:销售单价每上涨1元,则每天少售出5瓶.若设这款洗手液的销售单价上涨x元,每天的销售量利润为y元.
(1)每天的销售量为 瓶,每瓶洗手液的利润是 元;(用含x的代数式表示)
(2)若这款洗手液的日销售利润y达到300元,则销售单价应上涨多少元?
(3)当销售单价上涨多少元时,这款洗手液每天的销售利润y最大,最大利润为多少元?
21.某游乐场的圆形喷水池中心O有一雕塑OA,从A点向四周喷水,喷出的水柱为抛物线,且形状相同.如图,以水平方向为x轴,点O为原点建立直角坐标系,点A在y轴上,x轴上的点C,D为水柱的落水点,水柱所在抛物线(第一象限部分)的函数表达式为y=﹣(x﹣5)2+6.
(1)求雕塑高OA.
(2)求落水点C,D之间的距离.
(3)若需要在OD上的点E处竖立雕塑EF,OE=10m,EF=1.8m,EF⊥OD.问:顶部F是否会碰到水柱?请通过计算说明.
22.如图,有长为24米的篱笆,一面利用墙(墙的最大可用长度为10米)围成中间隔有一道篱笆的长方形花圃.设花圃AB边为x米,面积为y平方米.
(1)求y与x的函数关系式,并写出x的取值范围;
(2)如果要围成面积为45m2的花圃,求AB的长度;
(3)如果要使围成的花圃面积最大,求最大面积是多少m2.
23.如图,钢球从斜面顶端由静止开始沿斜面滚下,速度每秒增加1.5m.
(1)写出滚动的距离s(单位:m)关于滚动的时间t(单位:s)的函数解析式.(提示:本题中,距离=平均速度×时间t,=,其中,v0是开始时的速度,vt是t秒时的速度.)
(2)如果斜面的长是3m,钢球从斜面顶端滚到底端用多长时间?
24.设a、b是任意两个实数,用max{a,b}表示a、b两数中较大者,例如:max{﹣1,﹣1}=﹣1,max{1,2}=2,参照上面的材料,解答下列问题:
(1)max{5,2}= ,max{0,3}= ;
(2)若max{3x+1,﹣x+1}=﹣x+1,求x的取值范围;
(3)①求函数y=x2﹣2x﹣4与y=﹣x+2的图象的交点坐标.
②函数y=x2﹣2x﹣4的图象如图所示,请你在图中作出函数y=﹣x+2的图象,并根据图象直接写出max{﹣x+2,x2﹣2x﹣4}的最小值.
参考答案
一.选择题(共10小题,满分30分)
1.解:①由图象可知,小球在空中达到的最大高度为40m,则小球在空中经过的路程一定大于40m,故①错误;
②由图象可知,小球6s时落地,故小球运动的时间为6s,故②正确;
③小球抛出3秒时达到最高点,即速度为0,故③正确;
④设函数解析式为h=a(t﹣3)2+40,将(0,0)代入得:
0=a(0﹣3)2+40,
解得a=﹣,
∴函数解析式为h=﹣(t﹣3)2+40,
∴当t=1.5s时,h=﹣(1.5﹣3)2+40=30,
∴④正确.
综上,正确的有②③④.
故选:C.
2.解:令y=﹣=0
则:x2﹣8x﹣20=0
∴(x+2)(x﹣10)=0
∴x1=﹣2(舍),x2=10
由题意可知当x=10时,符合题意
故选:B.
3.解:∵礼炮在点火升空到最高点引爆,
∴t=﹣==6(s),
故选:D.
4.解:由题意可得,设抛物线解析式为:y=ax2,且抛物线过(2,﹣2)点,
故﹣2=a×22,
解得:a=﹣0.5,
∴抛物线解析式为:y=﹣0.5x2,
当水面宽度为6m时,即x=3时,
y=﹣0.5×9=﹣4,
∴水面下降﹣2﹣(﹣4)=2(m),
故选:D.
5.解:∵h=﹣t2+20t+1,
∴h=﹣(t﹣4)2+41,
∴顶点坐标为(4,41),
∴到达最高处的时间为4s.
故选:B.
6.解:根据题意,设抛物线解析式为y=a(x﹣2)2+k,
将点C(0,8)、B(8,0)代入,得:
,
解得,
∴抛物线解析式为y=﹣(x﹣2)2+9,
所以当x=2时,y=9,即AD=9m,
故选:A.
7.解:在y=﹣x2+x+中,当y=0时,﹣x2+x+=0,
解得x1=﹣2(舍去),x2=10,
即小强此次成绩为10米,
故选:B.
8.解:每顶头盔降价x元,利润为w元,
由题意可得,w=(80﹣x﹣50)(200+20x)=﹣20(x﹣10)2+8000,
∴当x=10时,w取得最大值,此时80﹣x=70,
即该商店每月获得最大利润时,每顶头盔的售价为70元,
故选:C.
9.解:观察图象可知,图象具有对称性,对称轴是直线x=﹣=1,故①正确;
令|x2﹣2x﹣3|=0可得x2﹣2x﹣3=0,
∴(x+1)(x﹣3)=0,
∴x1=﹣1,x2=3,
∴(﹣1,0)和(3,0)是函数图象与x轴的交点坐标,
又对称轴是直线x=1,
∴当﹣1<x<1或x>3时,函数值y随x值的增大而增大,故②正确;
由图象可知(﹣1,0)和(3,0)是函数图象的最低点,则当x=﹣1或x=3时,函数最小值是0,故③正确;
由图象可知,当x<﹣1时,函数值随x的减小而增大,当x>3时,函数值随x的增大而增大,均存在大于顶点坐标的函数值,
故当x=1时的函数值4并非最大值,故④错误.
综上,只有④错误.
故选:B.
10.解:由题意函数关系p=at2+bt+c(a,b,c是常数)经过点(3,0.7),(4,0.8),(5,0.5),
代入得:,
解得:,
∴p=﹣0.2t2+1.5t﹣2.2=﹣0.2(t﹣3.75)2+0.6125,
∴得到最佳加工时间为3.75分钟.
故选:B.
二.填空题(共8小题,满分32分)
11.解:∵s=12t﹣6t2=﹣6(t﹣1)2+6,
∴当t=1时,s取得最大值6,
即当t=1时,汽车刹车后行驶的距离s取得最大值6m,
∴汽车刹车后到停下来前进了6m,
故答案为:6.
12.解:设销售单价定为x元(x≥9),每天所获利润为y元,
则y=[20﹣4(x﹣9)] (x﹣8)
=﹣4x2+88x﹣448
=﹣4(x﹣11)2+36,
所以将销售定价定为11元时,才能使每天所获销售利润最大,
故答案为11.
13.解:由图象可知抛物线顶点坐标(20,16),经过(0,0),(40,0).
设抛物线的解析式为y=a(x﹣20)2+16,把(0,0)代入得到a=﹣,
∴抛物线的解析式为y=﹣(x﹣20)2+16,
即y=﹣x2+x,
故答案为:y=﹣x2+x.
14.解:建立坐标系,如图所示:
由题意得:A(0,1.68),B(2,2),点B为抛物线的顶点,
设抛物线的解析式为y=a(x﹣2)2+2,
把A(0,1.68)代入得:
4a+2=1.68,
解得a=﹣0.08,
∴y=﹣0.08(x﹣2)2+2,
令y=0,得﹣0.08(x﹣2)2+2=0,
解得x1=7,x2=﹣3(舍),
∴小丁此次投掷的成绩是7米.
故答案为:7.
15.解:∵y=﹣2x2+4x+1=﹣2(x﹣1)2+3,
∴当x=1时,y有最大值为3,
∴喷出水珠的最大高度是3m,
故答案为:3.
16.解:∵AB=6m,OC=3m,
∴点B坐标为(3,﹣3),
将B(3,﹣3)代入y=ax2得:
﹣3=a×32,
∴a=﹣,
∴y=﹣x2.
∴当水面上升1m时,即纵坐标y=﹣2时,有:
﹣2=﹣x2,
∴x2=6,
∴x1=﹣,x2=.
∴水面宽为:﹣(﹣)=2(m).
故答案为:2.
17.解:若和墙相邻的一边长为x米,则平行于墙的一边长为(30+1﹣2x)米,
依题意得:y=x(30+1﹣2x)=﹣2x2+31x.
又∵,
∴8≤x<15.5,
∴y与x之间的函数关系式为y=﹣2x2+31x(8≤x<15.5).
故答案为:y=﹣2x2+31x(8≤x<15.5).
18.解:∵y=40+=﹣x+240,
∴①正确,②错误;
∵w=(x﹣100)(﹣x+240)=﹣+320x﹣24000;
∴③正确;
∵w=(x﹣100)(﹣x+240)=﹣+320x﹣24000=﹣(x﹣200)2+8000,
a=﹣<0,每件售价不得低于210元,
所以当x=210时,每天利润最大是7920元,
∴④正确.
故答案为:①③④.
三.解答题(共6小题,满分58分)
19.解:(1)令x=0代入,
∴y=.
(2),
解得x1=10,x2=﹣2(舍去)
∴铅球推出的水平距离为10米.
(3)把y=4代入,得,
化简得x2﹣8x+28=0,方程无解,
∴铅球的行进高度不能达到4米.
20.解:(1)每天的销售量为(60﹣5x)瓶,每瓶洗手液的利润是(4+x)元;
故答案为:(60﹣5x);(4+x);
(2)根据题意得,(60﹣5x)(4+x)=300,
解得:x1=6,x2=2,
答:销售单价应上涨2元或6元;
(3)根据题意得,y=(60﹣5x)(4+x)=﹣5(x﹣12)(x+4)=﹣5(x﹣4)2+320,
答:当销售单价上涨4元时,这款洗手液每天的销售利润y最大,最大利润为320元.
21.解:(1)当x=0时,y=﹣(0﹣5)2+6=,
∴点A的坐标为(0,),
∴雕塑高m.
(2)当y=0时,﹣(x﹣5)2+6=0,
解得:x1=﹣1(舍去),x2=11,
∴点D的坐标为(11,0),
∴OD=11m.
∵从A点向四周喷水,喷出的水柱为抛物线,且形状相同,
∴OC=OD=11m,
∴CD=OC+OD=22m.
(3)当x=10时,y=﹣(10﹣5)2+6=,
∴点(10,)在抛物线y=﹣(x﹣5)2+6上.
又∵≈1.83>1.8,
∴顶部F不会碰到水柱.
22.解:(1)由题可知,花圃的宽AB为x米,则BC为(24﹣3x)米,
这时面积y=x(24﹣3x)=﹣3x2+24x,
∵0<24﹣3x≤10,
解得:≤x<8,
∴y=﹣3x2+24x(≤x<8);
(2)由条件﹣3x2+24x=45,
化简得x2﹣8x+15=0,
解得x1=5,x2=3,
∴x=3不合题意,舍去,
即AB的长度为5米;
(3)y=﹣3x2+24x=﹣3(x2﹣8x)=﹣3(x﹣4)2+48(≤x<8),
∵a=﹣3<0,开口向下,
∴当x=时,y有最大值48﹣3(﹣4)2=46,
故最大面积为46m2.
23.解:(1)由已知得vt=v0+at=0+1.5t=1.5t,
∴==,
∴s=t= t= t=t2,即s=t2;
(2)把s=3代入s=t2中,得t=2(t=﹣2舍去).
即钢球从斜面顶端滾到底端用2s.
答:钢球从斜面顶端滾到底端用2s.
24.解:(1)∵5>2,
∴max{5,2}=5,
∵3>0,
∴max{0,3}=3,
故答案为:5,3.
(2)∵max{3x+1,﹣x+1}=﹣x+1,
∴﹣x+1≥3x+1,
解得x≤0.
(3)①联立方程,
解得,,
∴函数y=x2﹣2x﹣4与y=﹣x+2的图象的交点坐标为(﹣2,4),(3,﹣1).
②如图,
∵图象交点为(﹣2,4),(3,﹣1),
∴当x≤﹣2时,x2﹣2x﹣4≥﹣x+2,且x2﹣2x﹣4≥4,
当﹣2<x<3时,﹣x+2>x2﹣2x﹣4,且﹣1<﹣x+2<4,
当x≥3时,x2﹣2x﹣4≥﹣x+2,且x2﹣2x﹣4≥﹣1,
综上所述,max{﹣x+2,x2﹣2x﹣4}的最小值为﹣1.
