2021-2022学年人教版九年级数学下册28.2解直角三角形及其应用 题型分类练习(word版含解析)
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册28.2解直角三角形及其应用 题型分类练习(word版含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 584.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-28 00:00:00 | ||
图片预览

文档简介
2021-2022学年人教版九年级数学下册《28.2解直角三角形及其应用》
题型分类练习(附答案)
一.网格问题
1.如图,在正方形网格中,已知△ABC的三个顶点均在格点上,则sin∠CAB=( )
A.2 B. C. D.
2.如图,在5×4的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在这些小正方形的顶点上,则cos∠BAC的值为( )
A. B. C. D.
3.如图,正方形网格中每个小正方形的边长都是1,若点A、B、C都在格点上,则tan∠BAC的值是 .
4.如图,在正方形网格中,已知△ABC的三个顶点均在格点上,则∠ACB的正弦值为( )
A.2 B. C. D.
5.在如图所示的网格中,小正方形的边长均为1,△ABC的顶点都是格点,则sin∠BAC的值为( )
A. B. C.2 D.
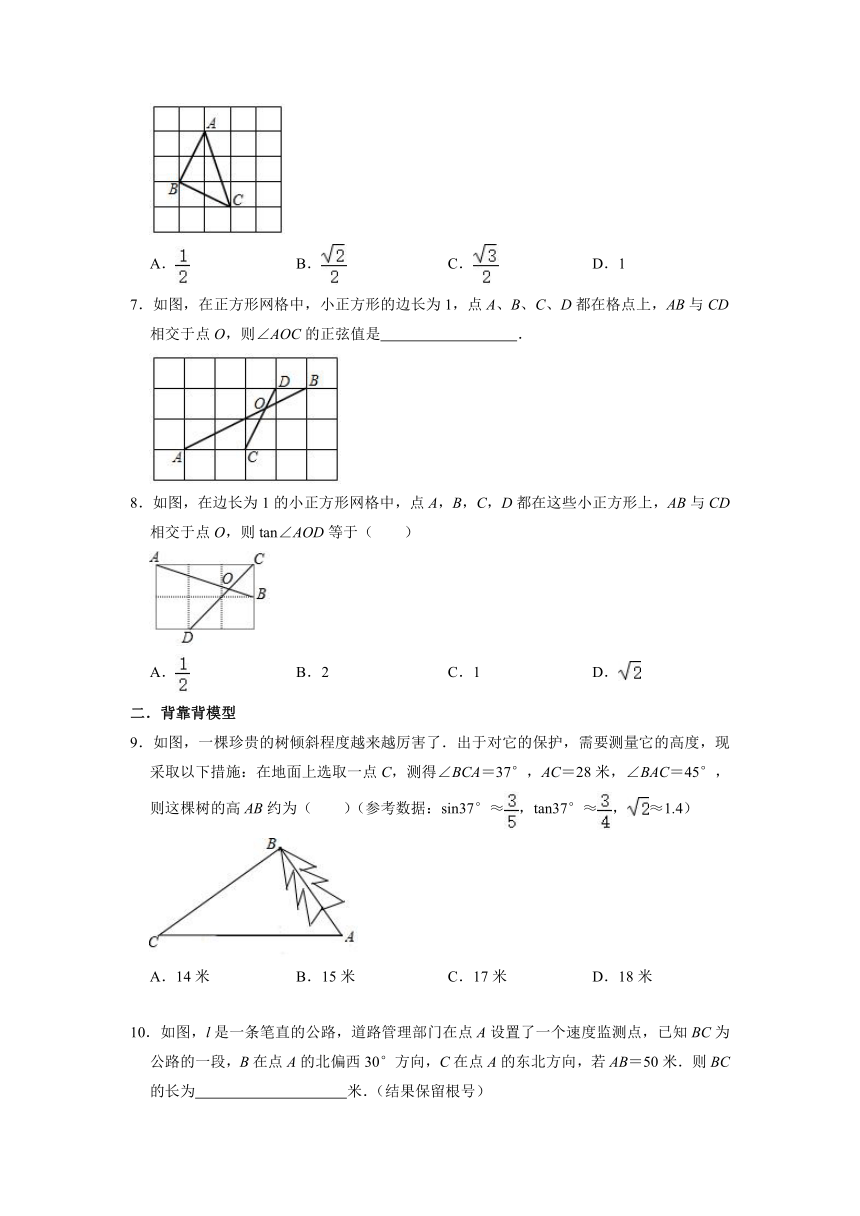
6.如图,已知△ABC的三个顶点均在以正方形组成的表格的格点上,则sinA的值是( )
A. B. C. D.1
7.如图,在正方形网格中,小正方形的边长为1,点A、B、C、D都在格点上,AB与CD相交于点O,则∠AOC的正弦值是 .
8.如图,在边长为1的小正方形网格中,点A,B,C,D都在这些小正方形上,AB与CD相交于点O,则tan∠AOD等于( )
A. B.2 C.1 D.
二.背靠背模型
9.如图,一棵珍贵的树倾斜程度越来越厉害了.出于对它的保护,需要测量它的高度,现采取以下措施:在地面上选取一点C,测得∠BCA=37°,AC=28米,∠BAC=45°,则这棵树的高AB约为( )(参考数据:sin37°≈,tan37°≈,≈1.4)
A.14米 B.15米 C.17米 D.18米
10.如图,l是一条笔直的公路,道路管理部门在点A设置了一个速度监测点,已知BC为公路的一段,B在点A的北偏西30°方向,C在点A的东北方向,若AB=50米.则BC的长为 米.(结果保留根号)
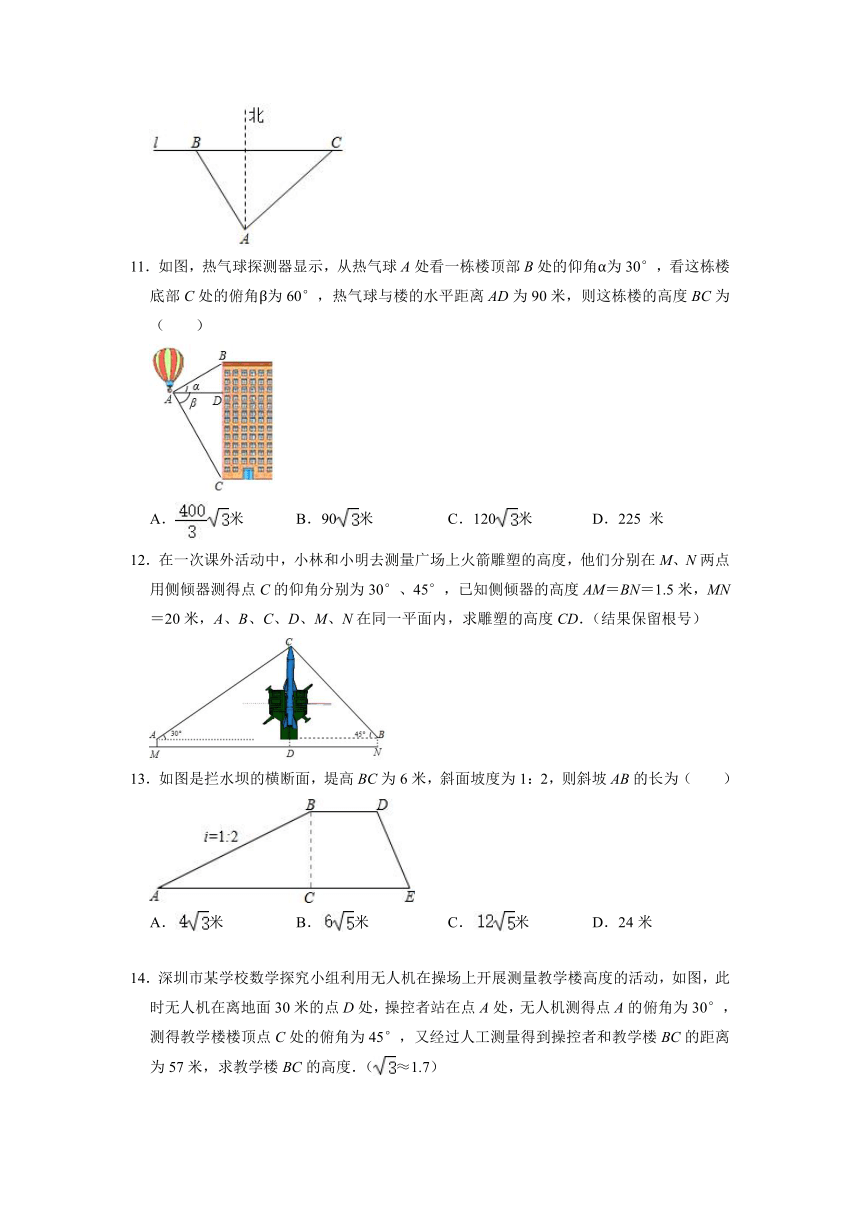
11.如图,热气球探测器显示,从热气球A处看一栋楼顶部B处的仰角α为30°,看这栋楼底部C处的俯角β为60°,热气球与楼的水平距离AD为90米,则这栋楼的高度BC为( )
A.米 B.90米 C.120米 D.225 米
12.在一次课外活动中,小林和小明去测量广场上火箭雕塑的高度,他们分别在M、N两点用侧倾器测得点C的仰角分别为30°、45°,已知侧倾器的高度AM=BN=1.5米,MN=20米,A、B、C、D、M、N在同一平面内,求雕塑的高度CD.(结果保留根号)
13.如图是拦水坝的横断面,堤高BC为6米,斜面坡度为1:2,则斜坡AB的长为( )
A.米 B.米 C.米 D.24米
14.深圳市某学校数学探究小组利用无人机在操场上开展测量教学楼高度的活动,如图,此时无人机在离地面30米的点D处,操控者站在点A处,无人机测得点A的俯角为30°,测得教学楼楼顶点C处的俯角为45°,又经过人工测量得到操控者和教学楼BC的距离为57米,求教学楼BC的高度.(≈1.7)
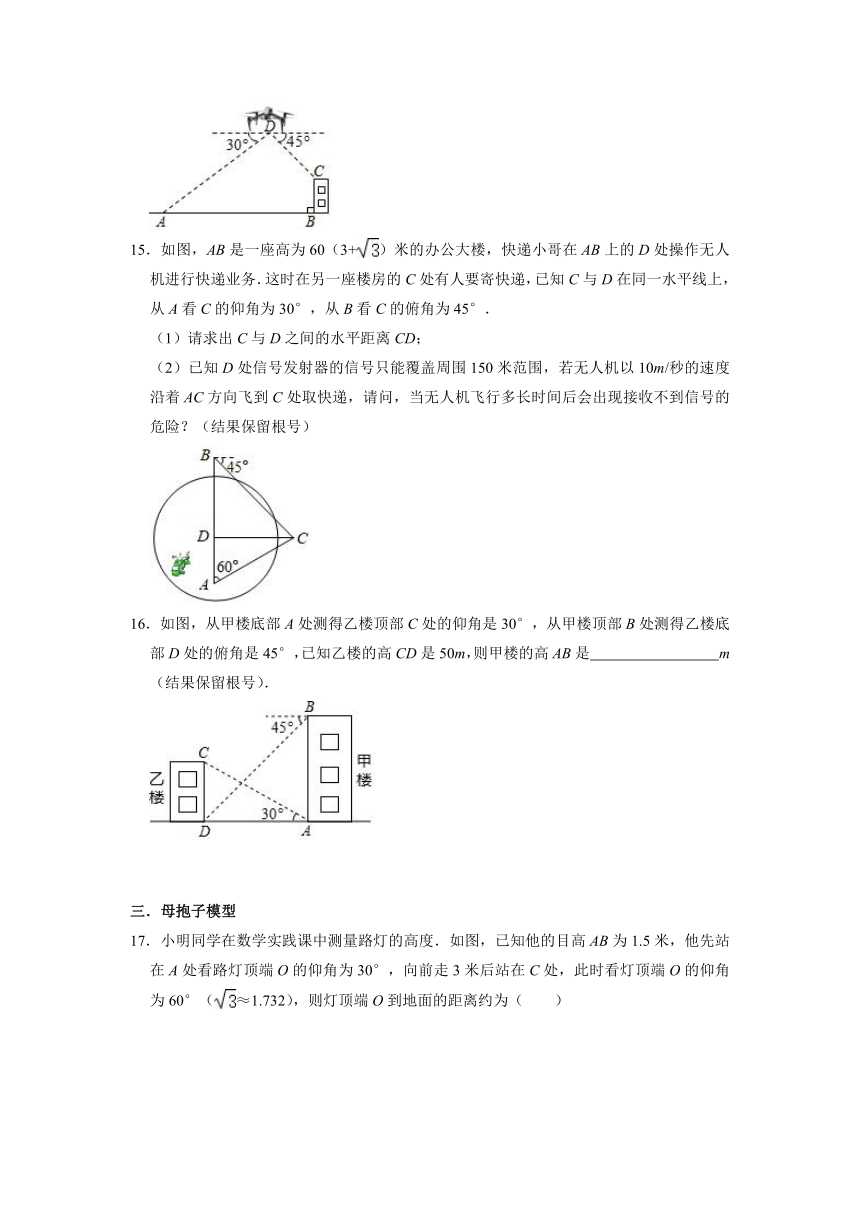
15.如图,AB是一座高为60(3+)米的办公大楼,快递小哥在AB上的D处操作无人机进行快递业务.这时在另一座楼房的C处有人要寄快递,已知C与D在同一水平线上,从A看C的仰角为30°,从B看C的俯角为45°.
(1)请求出C与D之间的水平距离CD;
(2)已知D处信号发射器的信号只能覆盖周围150米范围,若无人机以10m/秒的速度沿着AC方向飞到C处取快递,请问,当无人机飞行多长时间后会出现接收不到信号的危险?(结果保留根号)
16.如图,从甲楼底部A处测得乙楼顶部C处的仰角是30°,从甲楼顶部B处测得乙楼底部D处的俯角是45°,已知乙楼的高CD是50m,则甲楼的高AB是 m(结果保留根号).
三.母抱子模型
17.小明同学在数学实践课中测量路灯的高度.如图,已知他的目高AB为1.5米,他先站在A处看路灯顶端O的仰角为30°,向前走3米后站在C处,此时看灯顶端O的仰角为60°(≈1.732),则灯顶端O到地面的距离约为( )
A.3.2米 B.4.1米 C.4.7米 D.5.4米
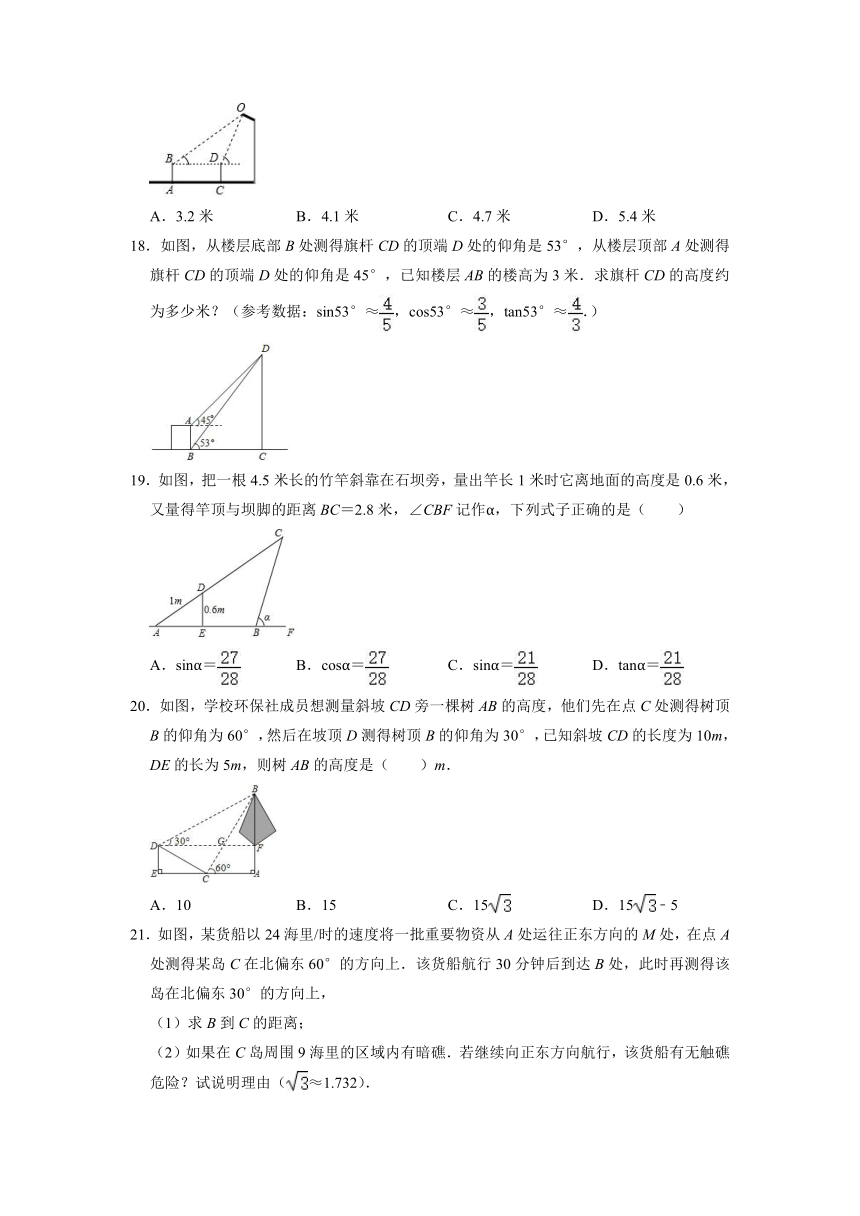
18.如图,从楼层底部B处测得旗杆CD的顶端D处的仰角是53°,从楼层顶部A处测得旗杆CD的顶端D处的仰角是45°,已知楼层AB的楼高为3米.求旗杆CD的高度约为多少米?(参考数据:sin53°≈,cos53°≈,tan53°≈.)
19.如图,把一根4.5米长的竹竿斜靠在石坝旁,量出竿长1米时它离地面的高度是0.6米,又量得竿顶与坝脚的距离BC=2.8米,∠CBF记作α,下列式子正确的是( )
A.sinα= B.cosα= C.sinα= D.tanα=
20.如图,学校环保社成员想测量斜坡CD旁一棵树AB的高度,他们先在点C处测得树顶B的仰角为60°,然后在坡顶D测得树顶B的仰角为30°,已知斜坡CD的长度为10m,DE的长为5m,则树AB的高度是( )m.
A.10 B.15 C.15 D.15﹣5
21.如图,某货船以24海里/时的速度将一批重要物资从A处运往正东方向的M处,在点A处测得某岛C在北偏东60°的方向上.该货船航行30分钟后到达B处,此时再测得该岛在北偏东30°的方向上,
(1)求B到C的距离;
(2)如果在C岛周围9海里的区域内有暗礁.若继续向正东方向航行,该货船有无触礁危险?试说明理由(≈1.732).
22.如图,某数学兴趣小组为测量一棵古树BH和教学楼CG的高,先在A处用高2米的测角仪测得古树顶端H的仰角∠HDE为45°,此时教学楼顶端G恰好在视线DH上,再向前走6米到达B处,又测得教学楼顶端G的仰角∠GEF为60°,点A、B、C三点在同一水平线上.
(1)计算古树BH的高;
(2)计算教学楼CG的高.(结果保留根号)
23.位于河南省登封市境内的元代观星台,是中国现存最早的天文台,也是世界文化遗产之一.
某校数学社团的同学们使用卷尺和自制的测角仪测量观星台的高度.如图所示,他们在地面一条水平步道MP上架设测角仪,先在点M处测得观星台最高点A的仰角为22°,然后沿MP方向前进16m到达点N处,测得点A的仰角为45°.测角仪的高度为1.6m求观星台最高点A距离地面的高度(结果精确到0.1m.参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,≈1.41).
四.坡比问题
24.如图,坡面CD的坡比为,坡顶的平地BC上有一棵小树AB,当太阳光线与水平线夹角成60°时,测得小树的在坡顶平地上的树影BC=3米,斜坡上的树影CD=米,则小树AB的高是 .
25.如图所示,游客到某知名景区大门后,需要先在大门口A处乘坐缆车从空中索道行走约2000米到达B处,再沿坡度为1:4的水泥路从B处步行约1000米到C处才能到达景区的景点.已知该索道与地面的夹角是37°,求景点C比景区大门A高约多少米.
(注:结果精确到0.1米.参考数据:sin37°≈0.6018,cos37°≈0.7986,tan37°≈0.7536,≈2.236,≈3.873,≈4.123)
26.已知如图,斜坡AP的坡度为1:2.4,斜坡AP的水平长度为24米在坡顶A处的同一水平面上有一座古塔BC在斜坡底P处测得该塔的塔顶B的仰角为45°,在坡顶A处测得该塔
的塔顶B的仰角为60°.
求:(1)坡顶A到地面PQ的距离;
(2)古塔BC的高度(结果保留根号).
参考答案
一.网格问题
1.解:如图所示:
则AC==,
∴sin∠CAB===;
故选:B.
2.解:过点C作CD⊥AB于点D,
∵AD=3,CD=4,
∴由勾股定理可知:AC=5,
∴cos∠BAC==,
故选:C.
3.解:连接CD,∵∠CAD=∠ACD=45°,
∴∠ADC=90°,
由勾股定理得:AD=CD==,
∴tan∠BAC==1,
故答案为:1.
4.解:延长CB交网格于D,连接AD,如图所示:
则∠ADC=45°+45°=90°,
∵AD==,AC==,
∴∠ACB的正弦值===;
故选:C.
5.解:作CD⊥AB于D,
由图形可知BC=2,
由勾股定理得,AC==,AB==3,
由三角形的面积公式可得,×2×3=×3×DE,
解得,DE=,
∴sin∠BAC===,
故选:D.
6.解:过点B作BM⊥AC,垂足为M.
S△ABC=S长方形DFCE﹣S△AFC﹣S△ADB﹣S△BCE
=3×2﹣×2×1﹣×1×3﹣×1×2
=.
在Rt△AFC和Rt△ADB中,
AB===,
AC===.
∵S△ABC=AC BM,
∴××BM=,
∴BM=.
在Rt△ABM中,
sinA==.
解法二:由网格构造直角三角形可得,AC2=12+32=10,AB2=12+22=5,BC2=12+22=5,
∵AB2=AC2+BC2,
∴△ABC是等腰直角三角形,
∴∠A=∠C=45°,
∴sinA=sin45°=.
故选:B.
7.解:如图,连接BE,过点E作EF⊥AB于点F.
∵BD∥CE.BD=CE.
∴四边形DBEC是平行四边形.
∴BE∥DC.
∴∠ABE=∠AOC.
∵AB==2,
S△ABE=AB×EF=×2×EF=×2×3.
∴EF=.
在Rt△BEF中,
∵BE==,
∴sin∠ABE=
=
=.
∴sin∠AOC=.
故答案为:.
8.解:如图,连接BE,与CD交于点F,
∵四边形BCEH是正方形,
∴HF=CF=CH,BF=EF=BE,CH=BE,BE⊥CH,
∴BF=CF,
∵AC∥BH,
∴△ACO∽△BHO,
∴HO:CO=BH:AC=1:3,
∵CF=HF,
∴HO:HF=1:2,
∴HO=OF=,
在Rt△OBF中,tan∠BOF==2
∵∠AOD=∠BOF,
∴tan∠AOD=2.
故选:B.
二.背靠背模型
9.解:如图,作BH⊥AC于H.
∵∠BCH=37°,∠BHC=90°,
设BH=xm,
∴CH===,
∵∠A=45°,
∴AH=BH=x,
∴x+x=28,
∴x=12,
∴AB=AH=×12≈17(m)
故选:C.
10.解:如图所示,
由题意知AD⊥BC于点D,且∠BAD=30°,∠DAC=∠ACD=45°,
∵AB=50米,
∴BD=ABsin∠BAD=50×=25(米),AD=ABcos∠BAD=50×=25(米),
在Rt△ACD中,∵∠DAC=∠ACD=45°,
∴AC=CD=25(米),
则BC=BD+CD=25+25(米),
故答案为:(25+25).
11.解:由题意可得,
α=30°,β=60°,AD=90米,∠ADC=∠ADB=90°,
∴在Rt△ADB中,α=30°,AD=90米,
∴tanα=,
∴BD=30(米),
在Rt△ADC中,β=60°,AD=90米,
∴tanβ=,
∴CD=90(米),
∴BC=BD+CD=30+90=120(米),
即这栋楼的高度BC是120米.
故选:C.
12.解:连接AB交AD于E,如图:
则AB=MN=20米,ED=AM=1.5米,
由题意得:∠CAE=30°,∠CBE=45°,
∵CD⊥AB,
∴∠AEC=∠BEC=90°,
∴AE=CE,BE=CE,
∵AB=AE+BE,
∴CE+CE=20米,
解得:CE=10﹣10(米),
∴CD=CE+ED=10﹣10+1.5=10﹣(米);
答:雕塑的高度CD为(10﹣)米.
13.解:∵斜面坡度为1:2,BC=6m,
∴AC=12m,
则AB=(m).
故选:B.
14.解:过点D作DE⊥AB于E,过点C作CF⊥DE于F,
由题意得AB=57米,DE=30米,∠DAB=30°,∠DCF=45°,
在Rt△ADE中,tan∠DAE=,
∴AE==≈51(米),
∵AB=57米,
∴BE=AB﹣AE=6(米),
∵CB⊥BE,FE⊥BE,CF⊥EF,
∴四边形BCFE为矩形,
∴CF=BE=6(米),
在Rt△DFC中,∠CDF=45°,
∴DF=CF=6(米),
∴BC=EF=DE﹣DF=24(米).
答:教学楼BC的高度约为24米.
15.解:(1)由已知得,∠DAC=60°,∠DBC=45°,∠ADC=90°,
设AD=xm,
在Rt△ADC中,∵tan∠DAC=,
∴CD=ADtan∠DAC=x×tan60°=x,
在Rt△BCD中,
∵∠BCD=90°﹣∠DBC=45°=∠DBC,
∴BD=CD=x,
∵AB=AD+BD,
∴x+x=60(3+),
解得x=60,
∴CD=x=180(m),
答:C与D之间的水平距离CD为180m;
(2)过点D作DE⊥AC于点E,
设无人机飞到F处时出现接收不到信号的危险,
连接DF,则DF=150m,
在Rt△ADE中,
∵sin∠DAC=,cos∠DAC=,
∴DE=ADsin∠DAC=60sin60°=90(m),
AE=ADcos∠DAC=60cos60°=30(m),
在Rt△DEF中,根据勾股定理,得
EF===120(m),
∴AF=AE+EF=(30+120)m,
∴t===(3+12)秒.
答:当无人机飞行(3+12)秒后会出现接收不到信号的危险.
16.解:在Rt△ACD中,∵∠CAD=30°,CD=50,
∴AD==50×=50,
在Rt△ABD中,∵∠BDA=45°,
∴AB=AD=50(m),
故答案为:50.
三.母抱子模型
17.解:过点O作OE⊥AC于点F,延长BD交OE于点F.
设DF=x米,
∵tan60°=,
∴OF=x(米),
∴BF=(3+x)米,
∵tan30°=,
∴OF=(3+x) (米),
∴x=(3+x),
∴x=1.5,
∴OF=1.5×≈2.60(米),
∴OE≈2.60+1.5≈4.1(米),
故选:B.
18.解:过A作AE⊥CD于E,如图所示:
则BC=AE,∠AED=90°,
由题意得:∠DAE=45°,∠DBC=53°,AB=3米,
∴△ADE是等腰直角三角形,
∴AE=DE,
设BC=AE=DE=x米,则CD=(x+3)米,
∵tan∠DBC==tan53°≈,
∴≈,
解得:x≈9,
∴CD=9+3=12(米),
答:旗杆CD的高度约为12米.
19.解:作CF⊥AB于点F,
由题意得:=,
∵AD=1米,AC=4.5米,
∴,
解得:CF=2.7米,
∴sinα===,
故选:A.
20.解:在Rt△CDE中,
∵CD=10m,DE=5m,
∴sin∠DCE=,
∴∠DCE=30°.
∵∠ACB=60°,DF∥AE,
∴∠BGF=60°
∴∠ABC=30°,∠DCB=90°.
∵∠BDF=30°,
∴∠DBF=60°,
∴∠DBC=30°,
∴BC===10(m),
∴AB=BC sin60°=10×=15(m).
故选:B.
21.解:(1)由题意得:∠BAC=90°﹣60°=30°,∠MBC=90°﹣30°=60°,
∵∠MBC=∠BAC+∠ACB,
∴∠ACB=∠MBC﹣∠BAC=30°,
∴∠BAC=∠ACB,
∴BC=AB=24×=12(海里);
(2)该货船无触礁危险,理由如下:
过点C作CD⊥AD于点D,如图所示:
∵∠EAC=60°,∠FBC=30°,
∴∠CAB=30°,∠CBD=60°.
∴在Rt△CBD中,CD=BD.
在Rt△CAD中,AD=CD=3BD=AB+BD=12+BD,
∴BD=6.
∴CD=6.
∵6>9,
∴货船继续向正东方向行驶无触礁危险.
22.解:(1)由题意:四边形ABED是矩形,可得DE=AB=6(米),AD=BE=2(米),
在Rt△DEH中,∵∠EDH=45°,
∴HE=DE=6(米).
∴BH=EH+BE=6+2=8(米).
答:古树BH的高为8米;
(2)作HJ⊥CG于J.则△HJG是等腰三角形,四边形BCJH是矩形,
设HJ=GJ=BC=x.
在Rt△EFG中,tan60°=,
∴=,
∴x=3(+1),
∴GF=GJ+JF=x+6=(3+9)米,
∴CG=CF+FG=2+3+9=(11+3)米.
答:教学楼CG的高为(11+3)米.
23.解:过A作AD⊥PM于D,延长BC交AD于E,
则四边形BMNC,四边形BMDE是矩形,
∴BC=MN=16m,DE=CN=BM=1.6m,
∵∠AEC=90°,∠ACE=45°,
∴△ACE是等腰直角三角形,
∴CE=AE,
设AE=CE=x,
∴BE=16+x,
∵∠ABE=22°,
∴tan22°==≈0.40,
解得:x≈10.7(m),
∴AD≈10.7+1.6=12.3(m),
答:观星台最高点A距离地面的高度约为12.3m.
四.坡比问题
24.解:由已知得Rt△AFD,Rt△CED,如图,且得:∠ADF=60°,FE=BC,BF=CE,
在Rt△CED中,设CE=x,由坡面CD的坡比为,得:
DE=x,则根据勾股定理得:
x2+=,
得x=±,﹣不合题意舍去,
所以,CE=米,则,ED=米,
那么,FD=FE+ED=BC+ED=3+=米,
在Rt△AFD中,由三角函数得:
=tan∠ADF,
∴AF=FD tan60°=×=米,
∴AB=AF﹣BF=AF﹣CE=﹣=4米,
故答案为:4米.
25.解:作BD⊥AM于点D,CE⊥AM于点E,BF⊥CE于点F,
则四边形BDEF为矩形,
∴BD=EF,
在Rt△ABD中,sinA=,
则BD=AB sinA≈2000×0.6018=1203.6(米),
∴EF=1203.6(米),
设CF=x,
∵BC坡的坡度为1:4,
∴BF=4x,
由勾股定理得,BC2=CF2+BF2,即10002=x2+(4x)2,
解得,x≈242.5(米),即CF≈242.5(米),
∴CE=CF+EF=1203.6+242.5=1446.1(米),
答:景点C比景区大门A高约1446.1米.
26.解:(1)作AD⊥PQ于D,延长BC交PQ于E,
则四边形ADEC为矩形,
∴AD=CE,
∵斜坡AP的坡度为1:2.4,斜坡AP的水平长度为24米,
∴AD=10,即坡顶A到地面PQ的距离为10米;
(2)设BC=x米,
在Rt△ABC中,tan∠BAC=,即=,
解得,AC=x,
在Rt△BPE中,∠BPE=45°,
∴PE=BE,即24+x=x+10,
解得,x=21+7,
答:古塔BC的高度为(21+7)米.
题型分类练习(附答案)
一.网格问题
1.如图,在正方形网格中,已知△ABC的三个顶点均在格点上,则sin∠CAB=( )
A.2 B. C. D.
2.如图,在5×4的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在这些小正方形的顶点上,则cos∠BAC的值为( )
A. B. C. D.
3.如图,正方形网格中每个小正方形的边长都是1,若点A、B、C都在格点上,则tan∠BAC的值是 .
4.如图,在正方形网格中,已知△ABC的三个顶点均在格点上,则∠ACB的正弦值为( )
A.2 B. C. D.
5.在如图所示的网格中,小正方形的边长均为1,△ABC的顶点都是格点,则sin∠BAC的值为( )
A. B. C.2 D.
6.如图,已知△ABC的三个顶点均在以正方形组成的表格的格点上,则sinA的值是( )
A. B. C. D.1
7.如图,在正方形网格中,小正方形的边长为1,点A、B、C、D都在格点上,AB与CD相交于点O,则∠AOC的正弦值是 .
8.如图,在边长为1的小正方形网格中,点A,B,C,D都在这些小正方形上,AB与CD相交于点O,则tan∠AOD等于( )
A. B.2 C.1 D.
二.背靠背模型
9.如图,一棵珍贵的树倾斜程度越来越厉害了.出于对它的保护,需要测量它的高度,现采取以下措施:在地面上选取一点C,测得∠BCA=37°,AC=28米,∠BAC=45°,则这棵树的高AB约为( )(参考数据:sin37°≈,tan37°≈,≈1.4)
A.14米 B.15米 C.17米 D.18米
10.如图,l是一条笔直的公路,道路管理部门在点A设置了一个速度监测点,已知BC为公路的一段,B在点A的北偏西30°方向,C在点A的东北方向,若AB=50米.则BC的长为 米.(结果保留根号)
11.如图,热气球探测器显示,从热气球A处看一栋楼顶部B处的仰角α为30°,看这栋楼底部C处的俯角β为60°,热气球与楼的水平距离AD为90米,则这栋楼的高度BC为( )
A.米 B.90米 C.120米 D.225 米
12.在一次课外活动中,小林和小明去测量广场上火箭雕塑的高度,他们分别在M、N两点用侧倾器测得点C的仰角分别为30°、45°,已知侧倾器的高度AM=BN=1.5米,MN=20米,A、B、C、D、M、N在同一平面内,求雕塑的高度CD.(结果保留根号)
13.如图是拦水坝的横断面,堤高BC为6米,斜面坡度为1:2,则斜坡AB的长为( )
A.米 B.米 C.米 D.24米
14.深圳市某学校数学探究小组利用无人机在操场上开展测量教学楼高度的活动,如图,此时无人机在离地面30米的点D处,操控者站在点A处,无人机测得点A的俯角为30°,测得教学楼楼顶点C处的俯角为45°,又经过人工测量得到操控者和教学楼BC的距离为57米,求教学楼BC的高度.(≈1.7)
15.如图,AB是一座高为60(3+)米的办公大楼,快递小哥在AB上的D处操作无人机进行快递业务.这时在另一座楼房的C处有人要寄快递,已知C与D在同一水平线上,从A看C的仰角为30°,从B看C的俯角为45°.
(1)请求出C与D之间的水平距离CD;
(2)已知D处信号发射器的信号只能覆盖周围150米范围,若无人机以10m/秒的速度沿着AC方向飞到C处取快递,请问,当无人机飞行多长时间后会出现接收不到信号的危险?(结果保留根号)
16.如图,从甲楼底部A处测得乙楼顶部C处的仰角是30°,从甲楼顶部B处测得乙楼底部D处的俯角是45°,已知乙楼的高CD是50m,则甲楼的高AB是 m(结果保留根号).
三.母抱子模型
17.小明同学在数学实践课中测量路灯的高度.如图,已知他的目高AB为1.5米,他先站在A处看路灯顶端O的仰角为30°,向前走3米后站在C处,此时看灯顶端O的仰角为60°(≈1.732),则灯顶端O到地面的距离约为( )
A.3.2米 B.4.1米 C.4.7米 D.5.4米
18.如图,从楼层底部B处测得旗杆CD的顶端D处的仰角是53°,从楼层顶部A处测得旗杆CD的顶端D处的仰角是45°,已知楼层AB的楼高为3米.求旗杆CD的高度约为多少米?(参考数据:sin53°≈,cos53°≈,tan53°≈.)
19.如图,把一根4.5米长的竹竿斜靠在石坝旁,量出竿长1米时它离地面的高度是0.6米,又量得竿顶与坝脚的距离BC=2.8米,∠CBF记作α,下列式子正确的是( )
A.sinα= B.cosα= C.sinα= D.tanα=
20.如图,学校环保社成员想测量斜坡CD旁一棵树AB的高度,他们先在点C处测得树顶B的仰角为60°,然后在坡顶D测得树顶B的仰角为30°,已知斜坡CD的长度为10m,DE的长为5m,则树AB的高度是( )m.
A.10 B.15 C.15 D.15﹣5
21.如图,某货船以24海里/时的速度将一批重要物资从A处运往正东方向的M处,在点A处测得某岛C在北偏东60°的方向上.该货船航行30分钟后到达B处,此时再测得该岛在北偏东30°的方向上,
(1)求B到C的距离;
(2)如果在C岛周围9海里的区域内有暗礁.若继续向正东方向航行,该货船有无触礁危险?试说明理由(≈1.732).
22.如图,某数学兴趣小组为测量一棵古树BH和教学楼CG的高,先在A处用高2米的测角仪测得古树顶端H的仰角∠HDE为45°,此时教学楼顶端G恰好在视线DH上,再向前走6米到达B处,又测得教学楼顶端G的仰角∠GEF为60°,点A、B、C三点在同一水平线上.
(1)计算古树BH的高;
(2)计算教学楼CG的高.(结果保留根号)
23.位于河南省登封市境内的元代观星台,是中国现存最早的天文台,也是世界文化遗产之一.
某校数学社团的同学们使用卷尺和自制的测角仪测量观星台的高度.如图所示,他们在地面一条水平步道MP上架设测角仪,先在点M处测得观星台最高点A的仰角为22°,然后沿MP方向前进16m到达点N处,测得点A的仰角为45°.测角仪的高度为1.6m求观星台最高点A距离地面的高度(结果精确到0.1m.参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,≈1.41).
四.坡比问题
24.如图,坡面CD的坡比为,坡顶的平地BC上有一棵小树AB,当太阳光线与水平线夹角成60°时,测得小树的在坡顶平地上的树影BC=3米,斜坡上的树影CD=米,则小树AB的高是 .
25.如图所示,游客到某知名景区大门后,需要先在大门口A处乘坐缆车从空中索道行走约2000米到达B处,再沿坡度为1:4的水泥路从B处步行约1000米到C处才能到达景区的景点.已知该索道与地面的夹角是37°,求景点C比景区大门A高约多少米.
(注:结果精确到0.1米.参考数据:sin37°≈0.6018,cos37°≈0.7986,tan37°≈0.7536,≈2.236,≈3.873,≈4.123)
26.已知如图,斜坡AP的坡度为1:2.4,斜坡AP的水平长度为24米在坡顶A处的同一水平面上有一座古塔BC在斜坡底P处测得该塔的塔顶B的仰角为45°,在坡顶A处测得该塔
的塔顶B的仰角为60°.
求:(1)坡顶A到地面PQ的距离;
(2)古塔BC的高度(结果保留根号).
参考答案
一.网格问题
1.解:如图所示:
则AC==,
∴sin∠CAB===;
故选:B.
2.解:过点C作CD⊥AB于点D,
∵AD=3,CD=4,
∴由勾股定理可知:AC=5,
∴cos∠BAC==,
故选:C.
3.解:连接CD,∵∠CAD=∠ACD=45°,
∴∠ADC=90°,
由勾股定理得:AD=CD==,
∴tan∠BAC==1,
故答案为:1.
4.解:延长CB交网格于D,连接AD,如图所示:
则∠ADC=45°+45°=90°,
∵AD==,AC==,
∴∠ACB的正弦值===;
故选:C.
5.解:作CD⊥AB于D,
由图形可知BC=2,
由勾股定理得,AC==,AB==3,
由三角形的面积公式可得,×2×3=×3×DE,
解得,DE=,
∴sin∠BAC===,
故选:D.
6.解:过点B作BM⊥AC,垂足为M.
S△ABC=S长方形DFCE﹣S△AFC﹣S△ADB﹣S△BCE
=3×2﹣×2×1﹣×1×3﹣×1×2
=.
在Rt△AFC和Rt△ADB中,
AB===,
AC===.
∵S△ABC=AC BM,
∴××BM=,
∴BM=.
在Rt△ABM中,
sinA==.
解法二:由网格构造直角三角形可得,AC2=12+32=10,AB2=12+22=5,BC2=12+22=5,
∵AB2=AC2+BC2,
∴△ABC是等腰直角三角形,
∴∠A=∠C=45°,
∴sinA=sin45°=.
故选:B.
7.解:如图,连接BE,过点E作EF⊥AB于点F.
∵BD∥CE.BD=CE.
∴四边形DBEC是平行四边形.
∴BE∥DC.
∴∠ABE=∠AOC.
∵AB==2,
S△ABE=AB×EF=×2×EF=×2×3.
∴EF=.
在Rt△BEF中,
∵BE==,
∴sin∠ABE=
=
=.
∴sin∠AOC=.
故答案为:.
8.解:如图,连接BE,与CD交于点F,
∵四边形BCEH是正方形,
∴HF=CF=CH,BF=EF=BE,CH=BE,BE⊥CH,
∴BF=CF,
∵AC∥BH,
∴△ACO∽△BHO,
∴HO:CO=BH:AC=1:3,
∵CF=HF,
∴HO:HF=1:2,
∴HO=OF=,
在Rt△OBF中,tan∠BOF==2
∵∠AOD=∠BOF,
∴tan∠AOD=2.
故选:B.
二.背靠背模型
9.解:如图,作BH⊥AC于H.
∵∠BCH=37°,∠BHC=90°,
设BH=xm,
∴CH===,
∵∠A=45°,
∴AH=BH=x,
∴x+x=28,
∴x=12,
∴AB=AH=×12≈17(m)
故选:C.
10.解:如图所示,
由题意知AD⊥BC于点D,且∠BAD=30°,∠DAC=∠ACD=45°,
∵AB=50米,
∴BD=ABsin∠BAD=50×=25(米),AD=ABcos∠BAD=50×=25(米),
在Rt△ACD中,∵∠DAC=∠ACD=45°,
∴AC=CD=25(米),
则BC=BD+CD=25+25(米),
故答案为:(25+25).
11.解:由题意可得,
α=30°,β=60°,AD=90米,∠ADC=∠ADB=90°,
∴在Rt△ADB中,α=30°,AD=90米,
∴tanα=,
∴BD=30(米),
在Rt△ADC中,β=60°,AD=90米,
∴tanβ=,
∴CD=90(米),
∴BC=BD+CD=30+90=120(米),
即这栋楼的高度BC是120米.
故选:C.
12.解:连接AB交AD于E,如图:
则AB=MN=20米,ED=AM=1.5米,
由题意得:∠CAE=30°,∠CBE=45°,
∵CD⊥AB,
∴∠AEC=∠BEC=90°,
∴AE=CE,BE=CE,
∵AB=AE+BE,
∴CE+CE=20米,
解得:CE=10﹣10(米),
∴CD=CE+ED=10﹣10+1.5=10﹣(米);
答:雕塑的高度CD为(10﹣)米.
13.解:∵斜面坡度为1:2,BC=6m,
∴AC=12m,
则AB=(m).
故选:B.
14.解:过点D作DE⊥AB于E,过点C作CF⊥DE于F,
由题意得AB=57米,DE=30米,∠DAB=30°,∠DCF=45°,
在Rt△ADE中,tan∠DAE=,
∴AE==≈51(米),
∵AB=57米,
∴BE=AB﹣AE=6(米),
∵CB⊥BE,FE⊥BE,CF⊥EF,
∴四边形BCFE为矩形,
∴CF=BE=6(米),
在Rt△DFC中,∠CDF=45°,
∴DF=CF=6(米),
∴BC=EF=DE﹣DF=24(米).
答:教学楼BC的高度约为24米.
15.解:(1)由已知得,∠DAC=60°,∠DBC=45°,∠ADC=90°,
设AD=xm,
在Rt△ADC中,∵tan∠DAC=,
∴CD=ADtan∠DAC=x×tan60°=x,
在Rt△BCD中,
∵∠BCD=90°﹣∠DBC=45°=∠DBC,
∴BD=CD=x,
∵AB=AD+BD,
∴x+x=60(3+),
解得x=60,
∴CD=x=180(m),
答:C与D之间的水平距离CD为180m;
(2)过点D作DE⊥AC于点E,
设无人机飞到F处时出现接收不到信号的危险,
连接DF,则DF=150m,
在Rt△ADE中,
∵sin∠DAC=,cos∠DAC=,
∴DE=ADsin∠DAC=60sin60°=90(m),
AE=ADcos∠DAC=60cos60°=30(m),
在Rt△DEF中,根据勾股定理,得
EF===120(m),
∴AF=AE+EF=(30+120)m,
∴t===(3+12)秒.
答:当无人机飞行(3+12)秒后会出现接收不到信号的危险.
16.解:在Rt△ACD中,∵∠CAD=30°,CD=50,
∴AD==50×=50,
在Rt△ABD中,∵∠BDA=45°,
∴AB=AD=50(m),
故答案为:50.
三.母抱子模型
17.解:过点O作OE⊥AC于点F,延长BD交OE于点F.
设DF=x米,
∵tan60°=,
∴OF=x(米),
∴BF=(3+x)米,
∵tan30°=,
∴OF=(3+x) (米),
∴x=(3+x),
∴x=1.5,
∴OF=1.5×≈2.60(米),
∴OE≈2.60+1.5≈4.1(米),
故选:B.
18.解:过A作AE⊥CD于E,如图所示:
则BC=AE,∠AED=90°,
由题意得:∠DAE=45°,∠DBC=53°,AB=3米,
∴△ADE是等腰直角三角形,
∴AE=DE,
设BC=AE=DE=x米,则CD=(x+3)米,
∵tan∠DBC==tan53°≈,
∴≈,
解得:x≈9,
∴CD=9+3=12(米),
答:旗杆CD的高度约为12米.
19.解:作CF⊥AB于点F,
由题意得:=,
∵AD=1米,AC=4.5米,
∴,
解得:CF=2.7米,
∴sinα===,
故选:A.
20.解:在Rt△CDE中,
∵CD=10m,DE=5m,
∴sin∠DCE=,
∴∠DCE=30°.
∵∠ACB=60°,DF∥AE,
∴∠BGF=60°
∴∠ABC=30°,∠DCB=90°.
∵∠BDF=30°,
∴∠DBF=60°,
∴∠DBC=30°,
∴BC===10(m),
∴AB=BC sin60°=10×=15(m).
故选:B.
21.解:(1)由题意得:∠BAC=90°﹣60°=30°,∠MBC=90°﹣30°=60°,
∵∠MBC=∠BAC+∠ACB,
∴∠ACB=∠MBC﹣∠BAC=30°,
∴∠BAC=∠ACB,
∴BC=AB=24×=12(海里);
(2)该货船无触礁危险,理由如下:
过点C作CD⊥AD于点D,如图所示:
∵∠EAC=60°,∠FBC=30°,
∴∠CAB=30°,∠CBD=60°.
∴在Rt△CBD中,CD=BD.
在Rt△CAD中,AD=CD=3BD=AB+BD=12+BD,
∴BD=6.
∴CD=6.
∵6>9,
∴货船继续向正东方向行驶无触礁危险.
22.解:(1)由题意:四边形ABED是矩形,可得DE=AB=6(米),AD=BE=2(米),
在Rt△DEH中,∵∠EDH=45°,
∴HE=DE=6(米).
∴BH=EH+BE=6+2=8(米).
答:古树BH的高为8米;
(2)作HJ⊥CG于J.则△HJG是等腰三角形,四边形BCJH是矩形,
设HJ=GJ=BC=x.
在Rt△EFG中,tan60°=,
∴=,
∴x=3(+1),
∴GF=GJ+JF=x+6=(3+9)米,
∴CG=CF+FG=2+3+9=(11+3)米.
答:教学楼CG的高为(11+3)米.
23.解:过A作AD⊥PM于D,延长BC交AD于E,
则四边形BMNC,四边形BMDE是矩形,
∴BC=MN=16m,DE=CN=BM=1.6m,
∵∠AEC=90°,∠ACE=45°,
∴△ACE是等腰直角三角形,
∴CE=AE,
设AE=CE=x,
∴BE=16+x,
∵∠ABE=22°,
∴tan22°==≈0.40,
解得:x≈10.7(m),
∴AD≈10.7+1.6=12.3(m),
答:观星台最高点A距离地面的高度约为12.3m.
四.坡比问题
24.解:由已知得Rt△AFD,Rt△CED,如图,且得:∠ADF=60°,FE=BC,BF=CE,
在Rt△CED中,设CE=x,由坡面CD的坡比为,得:
DE=x,则根据勾股定理得:
x2+=,
得x=±,﹣不合题意舍去,
所以,CE=米,则,ED=米,
那么,FD=FE+ED=BC+ED=3+=米,
在Rt△AFD中,由三角函数得:
=tan∠ADF,
∴AF=FD tan60°=×=米,
∴AB=AF﹣BF=AF﹣CE=﹣=4米,
故答案为:4米.
25.解:作BD⊥AM于点D,CE⊥AM于点E,BF⊥CE于点F,
则四边形BDEF为矩形,
∴BD=EF,
在Rt△ABD中,sinA=,
则BD=AB sinA≈2000×0.6018=1203.6(米),
∴EF=1203.6(米),
设CF=x,
∵BC坡的坡度为1:4,
∴BF=4x,
由勾股定理得,BC2=CF2+BF2,即10002=x2+(4x)2,
解得,x≈242.5(米),即CF≈242.5(米),
∴CE=CF+EF=1203.6+242.5=1446.1(米),
答:景点C比景区大门A高约1446.1米.
26.解:(1)作AD⊥PQ于D,延长BC交PQ于E,
则四边形ADEC为矩形,
∴AD=CE,
∵斜坡AP的坡度为1:2.4,斜坡AP的水平长度为24米,
∴AD=10,即坡顶A到地面PQ的距离为10米;
(2)设BC=x米,
在Rt△ABC中,tan∠BAC=,即=,
解得,AC=x,
在Rt△BPE中,∠BPE=45°,
∴PE=BE,即24+x=x+10,
解得,x=21+7,
答:古塔BC的高度为(21+7)米.
