2021-2022学年苏科版九年级数学下册《7.6用锐角三角函数解决问题》达标测评(word解析版)
文档属性
| 名称 | 2021-2022学年苏科版九年级数学下册《7.6用锐角三角函数解决问题》达标测评(word解析版) |
|
|
| 格式 | doc | ||
| 文件大小 | 441.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-28 00:00:00 | ||
图片预览


文档简介
2021-2022学年苏科版九年级数学下册《7.6用锐角三角函数解决问题》达标测评(附答案)
一.选择题(共6小题,满分30分)
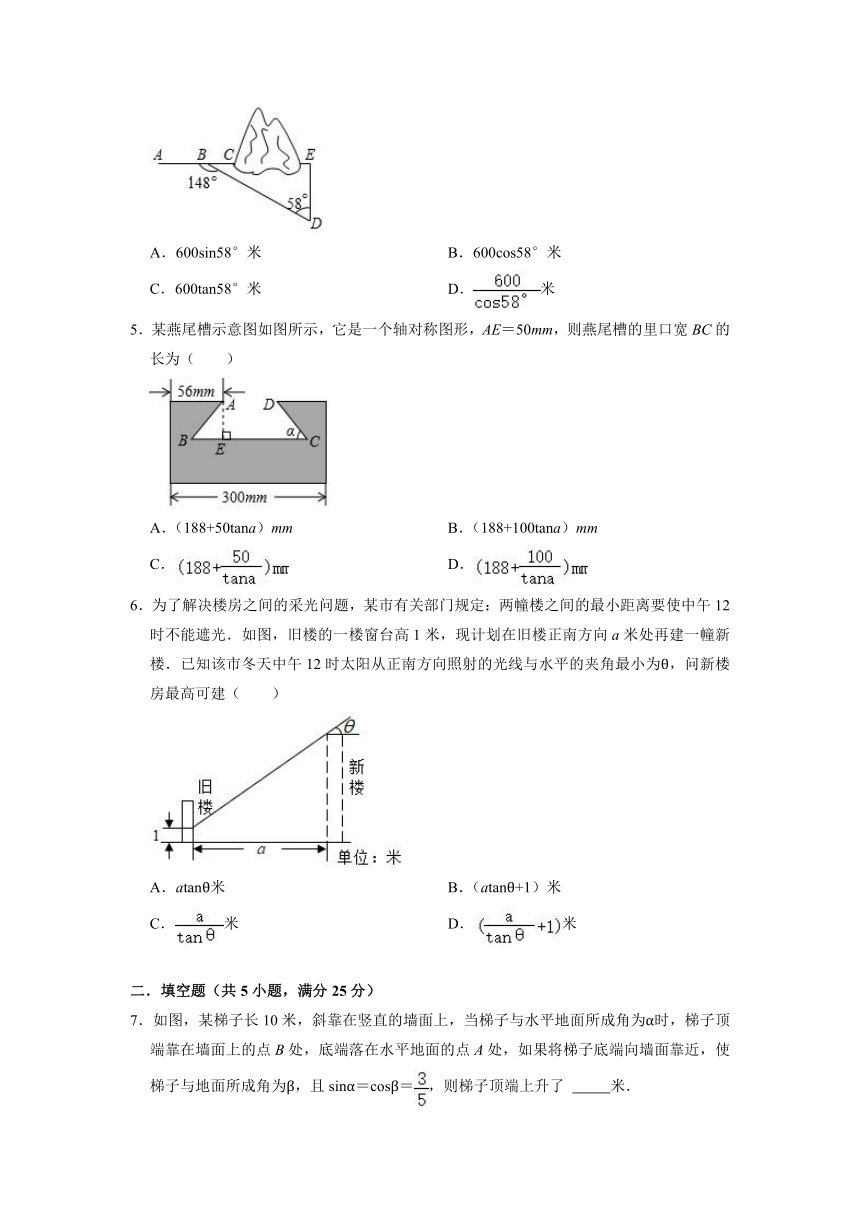
1.如图1,是我们经常看到的一种折叠桌子,它是由下面的支架AD、BC与桌面构成,如图2,已知OA=OB=OC=OD=20cm,∠COD=60°,则点A到地面(CD所在的平面)的距离是( )
A.30cm B.60cm C.40cm D.60cm
2.如图,A,B两地隔河相望,原来从A地到B地需要经过桥DC,沿折线A→D→C→B到达B地,现在AB(与桥DC平行)上建了新桥EF,可沿AB从A地直达B地.已知BC=500m.桥CD=50m,∠A=45°,∠B=30°.则AB的长是( )
A. B. C. D.500m
3.如图要测量小河两岸相对的两点P、A的距离,可以在小河边取PA的垂线PB上的一点C,测得PC=50米,∠PCA=44°,则小河宽PA为( )米.
A.50sin44° B.50cos44° C.50tan44° D.50tan46°
4.如图,沿AC的方向开山修路,为了加快速度,要在小山的另一边同时施工,从AC上取一点B,取∠ABD=148°,已知BD=600米,∠D=58°,DE⊥AE,点A、C、E在同一直线上,那么开挖点E离点D的距离是( )
A.600sin58°米 B.600cos58°米
C.600tan58°米 D.米
5.某燕尾槽示意图如图所示,它是一个轴对称图形,AE=50mm,则燕尾槽的里口宽BC的长为( )
A.(188+50tana)mm B.(188+100tana)mm
C. D.
6.为了解决楼房之间的采光问题,某市有关部门规定:两幢楼之间的最小距离要使中午12时不能遮光.如图,旧楼的一楼窗台高1米,现计划在旧楼正南方向a米处再建一幢新楼.已知该市冬天中午12时太阳从正南方向照射的光线与水平的夹角最小为θ,问新楼房最高可建( )
A.atanθ米 B.(atanθ+1)米
C.米 D.米
二.填空题(共5小题,满分25分)
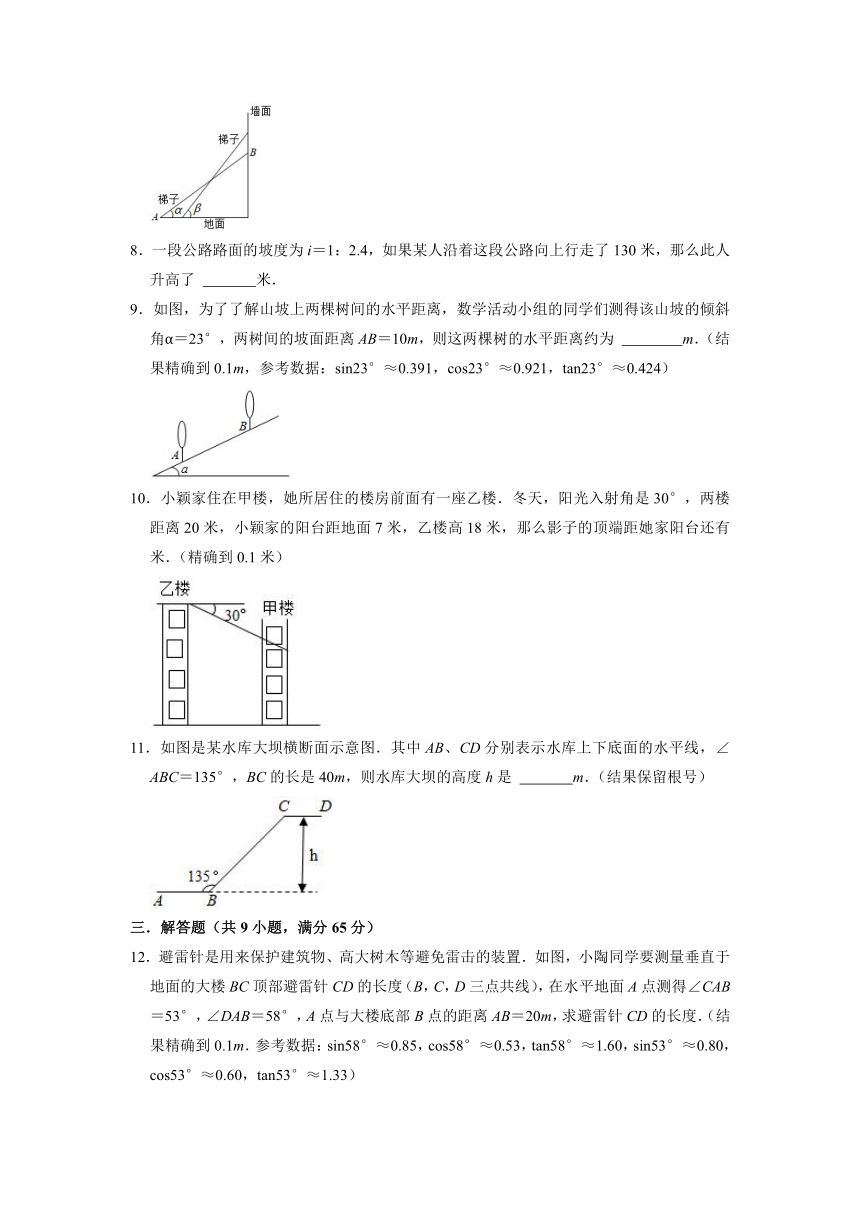
7.如图,某梯子长10米,斜靠在竖直的墙面上,当梯子与水平地面所成角为α时,梯子顶端靠在墙面上的点B处,底端落在水平地面的点A处,如果将梯子底端向墙面靠近,使梯子与地面所成角为β,且sinα=cosβ=,则梯子顶端上升了 米.
8.一段公路路面的坡度为i=1:2.4,如果某人沿着这段公路向上行走了130米,那么此人升高了 米.
9.如图,为了了解山坡上两棵树间的水平距离,数学活动小组的同学们测得该山坡的倾斜角α=23°,两树间的坡面距离AB=10m,则这两棵树的水平距离约为 m.(结果精确到0.1m,参考数据:sin23°≈0.391,cos23°≈0.921,tan23°≈0.424)
10.小颖家住在甲楼,她所居住的楼房前面有一座乙楼.冬天,阳光入射角是30°,两楼距离20米,小颖家的阳台距地面7米,乙楼高18米,那么影子的顶端距她家阳台还有 米.(精确到0.1米)
11.如图是某水库大坝横断面示意图.其中AB、CD分别表示水库上下底面的水平线,∠ABC=135°,BC的长是40m,则水库大坝的高度h是 m.(结果保留根号)
三.解答题(共9小题,满分65分)
12.避雷针是用来保护建筑物、高大树木等避免雷击的装置.如图,小陶同学要测量垂直于地面的大楼BC顶部避雷针CD的长度(B,C,D三点共线),在水平地面A点测得∠CAB=53°,∠DAB=58°,A点与大楼底部B点的距离AB=20m,求避雷针CD的长度.(结果精确到0.1m.参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60,sin53°≈0.80,cos53°≈0.60,tan53°≈1.33)
13.学校运动场的四角各有一盏探照灯,其中一盏探照灯B的位置如图所示,已知坡长AC=12m,坡角α为30°,灯光受灯罩的影响,最远端的光线与地面的夹角β为27°,最近端的光线恰好与地面交于坡面的底端C处,且与地面的夹角为60°,A、B、C、D在同一平面上.(结果精确到0.1m.参考数据:sin27°≈0.45,cos27°≈0.89,tan27°≈0.51,≈1.73.)
(1)求灯杆AB的高度;
(2)求CD的长度.
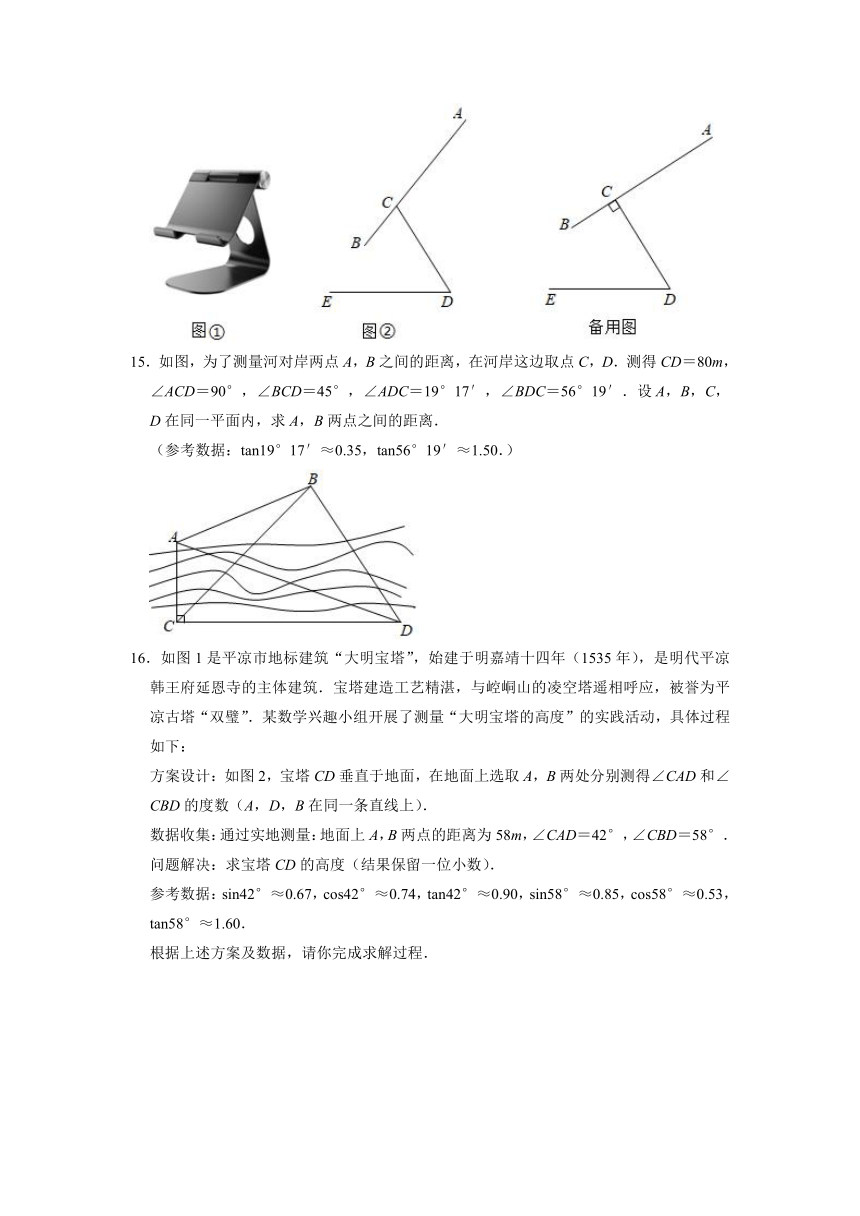
14.图①是一种手机平板支架,由托板、支撑板和底座构成,手机放置在托板上,图②是其侧面结构示意图,托板长AB=115mm,支撑板长CD=70mm,板AB固定在支撑板顶点C处,且CB=35mm,托板AB可绕点C转动,支撑板CD可绕点D转动,∠CDE=60°.
(1)若∠DCB=70°时,求点A到直线DE的距离(计算结果精确到个位);
(2)为了观看舒适,把(1)中∠DCB=70°调整为90°,再将CD绕点D逆时针旋转,使点B落在直线DE上即可,求CD旋转的角度.
(参考数据:sin50°≈0.8,cos50°≈0.6,tan50°≈1.2,sin26.6°≈0.4,cos26.6°≈0.9,tan26.6°≈0.5,≈1.7)
15.如图,为了测量河对岸两点A,B之间的距离,在河岸这边取点C,D.测得CD=80m,∠ACD=90°,∠BCD=45°,∠ADC=19°17′,∠BDC=56°19′.设A,B,C,D在同一平面内,求A,B两点之间的距离.
(参考数据:tan19°17′≈0.35,tan56°19′≈1.50.)
16.如图1是平凉市地标建筑“大明宝塔”,始建于明嘉靖十四年(1535年),是明代平凉韩王府延恩寺的主体建筑.宝塔建造工艺精湛,与崆峒山的凌空塔遥相呼应,被誉为平凉古塔“双璧”.某数学兴趣小组开展了测量“大明宝塔的高度”的实践活动,具体过程如下:
方案设计:如图2,宝塔CD垂直于地面,在地面上选取A,B两处分别测得∠CAD和∠CBD的度数(A,D,B在同一条直线上).
数据收集:通过实地测量:地面上A,B两点的距离为58m,∠CAD=42°,∠CBD=58°.
问题解决:求宝塔CD的高度(结果保留一位小数).
参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90,sin58°≈0.85,cos58°≈0.53,tan58°≈1.60.
根据上述方案及数据,请你完成求解过程.
17.学生到工厂劳动实践,学习制作机械零件.零件的截面如图阴影部分所示,已知四边形AEFD为矩形,点B、C分别在EF、DF上,∠ABC=90°,∠BAD=53°,AB=10cm,BC=6cm.求零件的截面面积.参考数据:sin53°≈0.80,cos53°≈0.60.
18.某一天,小明和小亮想利用所学过的测量知识来测量一棵古树的高度AB.他们带着测量工具来到这棵古树前,由于有围栏保护,他们无法到达古树的底部B,如图所示,于是他们先在古树周围的空地上选择一点D,通过测倾器测的角度为45°,再在BD的延长线上确定一点F,使DF=5米,并在F处通过测倾器测的角度为30°,测倾器的高度CD=EF=1米.已知点F、D、B在同一水平直线上,且EF、CD、AB均垂直于FB,则这棵古树的高度AB为多少米?(结果保留根号)
19.某型号飞机的机翼形状为如图所示的四边形ABDC,已知AB∥CD,∠C=45°,∠ABD=60°,CD长为3.4m.点B到CD的距离BE为5m,请根据以上数据计算AB的长度.
20.如图,地面上小山的两侧有A、B两地,为了测量A、B两地的距离,让一热气球从小山西侧A地出发沿与AB成30°角的方向,以每分钟50m的速度直线飞行,8分钟后到达C处,此时热气球上的人测得CB与AB成70°角,请你用测得的数据求A,B两地的距离AB长.(取1.7,sin20°取0.3,cos20°取0.9,tan20°取0.4,sin70°取0.9,cos70°取0.3,tan70°取2.7.)
参考答案
一.选择题(共6小题,满分30分)
1.解:如图,连接CD,过O作OF⊥CD于点F,延长FO,交AB于点E,
∵OA=OB=OC=OD=20cm,∠COD=60°,
∴∠COF=30°,
∴CF=OC cos∠COF==30(cm),
∴EF=2OF=60(cm),
即点A到地面(CD所在的平面)的距离是60cm.
故选:D.
2.解:过点C、D作DM⊥AB,CN⊥AB,垂足为M、N,
在Rt△BCN中,∠CBN=30°,BC=500m,
∴CN=BC=250(m)=DM,BN=BC=250(m),
在Rt△ADM中,∠DAM=45°,DM=250m,
∴AM=DM=250m,
∴AB=AM+MN+BN=250+50+250=(300+250)m,
故选:C.
3.解:∵PA⊥PB,
∴∠APC=90°,
∵PC=50米,∠PCA=44°,
∴tan44°=,
∴小河宽PA=PCtan∠PCA=50 tan44°(米).
故选:C.
4.解:∵∠DBE=180°﹣∠ABD=180°﹣148°=32°,
∴∠E=180°﹣32°﹣58°=90°,
∴△BDE是直角三角形,
∵BD=600米,cos∠D=,
∴开挖点E离点D的距离DE=600cos58°米.
故选:B.
5.解:如图,作AE⊥BC于点E,DF⊥BC于点F,
∵燕尾槽是一个轴对称图形,
∴∠B=∠C=α,AP=DQ=56mm,
∴EF=AD=300﹣112=188mm,
∴Rt△ABE中,BE==mm,
同理可得CF==mm,
∴BC=BE+EF+CF=(188+)mm.
故选:D.
6.解:如图,过点D作DE⊥AB与点E,
在Rt△ADE中,∠ADE=θ,DE=BC=a米,
则AE=tanθ DE=atanθ,
而EB=DC=1米,
∴AB=AE+EB=(atanθ+1)(米),
答:新楼房最高可建(atanθ+1)米,
故选:B.
二.填空题(共5小题,满分25分)
7.解:如图,由题意可知,∠ACB=90°,AB=ED=10,
由=sinα==cosβ=,
设BC=3m,则AB=5m,
则5m=10,
解得m=2,
∴BC=3×2=6,
设EC=3n,则ED=5n,
∴5n=10,
解得n=2,
∴EC=3×2=6,
∴DC===8,
∴BD=DC﹣BC=8﹣6=2(米),
∴梯子顶端上升了2米,
故答案为:2.
8.解:设此人升高了x米,
∵坡比为1:2.4,
∴他行走的水平宽度为2.4x米,
由勾股定理得,x2+(2.4x)2=1302,
解得,x=50,即他沿着垂直方向升高了50米,
故答案为:50.
9.解:过点A作水平面的平行线AC,过点B作BC⊥AC于C,
由题意得:AB=10m,∠BAC=23°,
则AC=AB cos∠BAC≈10×0.921≈9.2(米),
故答案为:9.2.
10.解:如图,
在Rt△ABC中,∠ABC=90°,∠ACB=30°,BC=20m,
∴AB=BC×tan30°=m≈11.55m,
CD=18﹣11.55=6.45m,
∴影子的顶端距她家的阳台还有7﹣6.45=0.55≈0.6m.
故答案为:0.6m.
11.解:如图,作CH⊥AB于点H.
∵∠ABC=135°,
∴∠CBH=45°,
∴CH=BC sin45°=40×=20(m),
故答案为:20.
三.解答题(共9小题,满分65分)
12.解:在Rt△ABD中,∵tan∠BAD=,
∴1.60=,
∴BD=32(米),
在Rt△CAD中,∵tan∠CAD=,
∴1.33=,
∴CD=26.6(米),
∴CD=BC﹣BD=5.4(米).
答:避雷针DC的长度为5.4米.
13.解:(1)延长BA交CG于点E,
则BE⊥CG,
在Rt△ACE中,∠ACE=30°,AC=12m,
∴AE=AC=×12=6(m),CE=AC cosα=12×=6(m),
在Rt△BCE中,∠BCE=60°,
∴BE=CE tan∠BCE=6×=18(m),
∴AB=BE﹣AE=18﹣6=12(m);
(2)在Rt△BDE中,∠BDE=27°,
∴CD=DE﹣CE=﹣6≈24.9(m).
14.解:(1)过点C作CG∥DE,过点A作AH⊥CG于H,过点C作CF⊥DE于点F,
则点A到直线DE的距离为:AH+CF.
在Rt△CDF中,
∵sin∠CDE=,
∴CF=CD sin60°=70×=35≈59.5(mm).
∵∠DCB=70°,
∴∠ACD=180°﹣∠DCB=110°,
∵CG∥DE,
∴∠GCD=∠CDE=60°.
∴∠ACH=∠ACD﹣∠DCG=50°.
在Rt△ACH中,
∵sin∠ACH=,
∴AH=AC sin∠ACH=(115﹣35)×sin50°≈80×0.8=64(mm).
∴点A到直线DE的距离为AH+CF=59.5+64=123.5≈124(mm).
(2)如下图所示,虚线部分为旋转后的位置,B的对应点为B′,C的对应点为C′,
则B′C′=BC=35 mm,DC′=DC=70 mm.
在Rt△B′C′D中,
∵tan∠B′DC′==0.5,tan26.6°≈0.5,
∴∠B′DC′=26.6°.
∴CD旋转的角度为∠CDC′=∠CDE﹣∠B′DC′=60°﹣26.6°=33.4°.
15.解:过B作BE⊥CD于E,过A作AF⊥BE于F,如图:
∵∠BCD=45°,
∴△BCE是等腰直角三角形,
设CE=x,则BE=x,
∵CD=80m,
∴DE=(80﹣x)m,
Rt△BDE中,∠BDC=56°19',
∴tan56°19'=,即=1.5,
解得x=48(m),
∴BE=CE=48m,
Rt△ACD中,∠ADC=19°17′,CD=80m,
∴tan19°17'=,即=0.35,
解得AC=28m,
∵∠ACD=90°,BE⊥CD于E,AF⊥BE,
∴四边形ACEF是矩形,
∴AF=CE=48m,EF=AC=28m,
∴BF=BE﹣EF=20m,
Rt△ABF中,AB===52(m),
答:A,B两点之间的距离是52m.
16.解:设CD=xm,
在Rt△ACD中,AD=,
在Rt△BCD中,BD=,
∵AD+BD=AB,
∴,
解得,x≈33.4.
答:宝塔的高度约为33.4m.
17.解:如图,
∵四边形AEFD为矩形,∠BAD=53°,
∴AD∥EF,∠E=∠F=90°,
∴∠BAD=∠EBA=53°,
在Rt△ABE中,∠E=90°,AB=10cm,∠EBA=53°,
∴sin∠EBA=≈0.80,cos∠EBA=≈0.60,
∴AE=8cm,BE=6cm,
∵∠ABC=90°,
∴∠FBC=90°﹣∠EBA=37°,
∴∠BCF=90°﹣∠FBC=53°,
在Rt△BCF中,∠F=90°,BC=6cm,
∴sin∠BCF=≈0.80,cos∠BCF=≈0.60,
∴BF=4.8cm,FC=3.6cm,
∴EF=6+4.8=10.8cm,
∴S四边形EFDA=AE EF=8×10.8=86.4(cm2),
S△ABE==×8×6=24(cm2),
S△BCF= BF CF=×4.8×3.6=8.64(cm2),
∴截面的面积=S四边形EFDA﹣S△ABE﹣S△BCF=86.4﹣24﹣8.64=53.76(cm2).
18.解:连接EC并延长交AB于点N,
由题意可得:EN⊥AB,四边形EFDC是矩形,
故FD=EC=5米,EF=DC=BN=1米,
则设AN=x米,故CN=x米,
可得:tan30°=,
解得:x=,
则AB=+1=(米),
答:这棵古树的高度AB为米.
19.解:由题意得BE⊥CE,过A作AH⊥CD于H,
则AH=BE=5m,EH=AB,
∵∠AHC=90°,∠C=45°,
∴CH=AH=5(m),
∴DH=CH﹣CD=5﹣3.4=1.6(m),
在Rt△BDE中,∵∠ABE=90°,∠ABD=60°,
∴∠DBE=30°,
∵BE=5,
∴DE=BE=×5=,
∴AB=HE=DE﹣DH=﹣1.6=.
20.解:过点C作CM⊥AB交AB延长线于点M,
由题意得:AC=50×8=400(m),
在Rt△ACM中,
∵∠A=30°,
∴CM=AC=200(m),AM=AC cos∠A=400×=200(m),
在Rt△BCM中,
∵∠CBM=70°,
∴∠BCM=20°,
∵tan20°=,
∴BM=200tan20°,
∴AB=AM﹣BM=200﹣200tan20°=200(﹣tan20°)=200(1.7﹣0.4)=260(m),
因此A,B两地的距离AB长为260m.
一.选择题(共6小题,满分30分)
1.如图1,是我们经常看到的一种折叠桌子,它是由下面的支架AD、BC与桌面构成,如图2,已知OA=OB=OC=OD=20cm,∠COD=60°,则点A到地面(CD所在的平面)的距离是( )
A.30cm B.60cm C.40cm D.60cm
2.如图,A,B两地隔河相望,原来从A地到B地需要经过桥DC,沿折线A→D→C→B到达B地,现在AB(与桥DC平行)上建了新桥EF,可沿AB从A地直达B地.已知BC=500m.桥CD=50m,∠A=45°,∠B=30°.则AB的长是( )
A. B. C. D.500m
3.如图要测量小河两岸相对的两点P、A的距离,可以在小河边取PA的垂线PB上的一点C,测得PC=50米,∠PCA=44°,则小河宽PA为( )米.
A.50sin44° B.50cos44° C.50tan44° D.50tan46°
4.如图,沿AC的方向开山修路,为了加快速度,要在小山的另一边同时施工,从AC上取一点B,取∠ABD=148°,已知BD=600米,∠D=58°,DE⊥AE,点A、C、E在同一直线上,那么开挖点E离点D的距离是( )
A.600sin58°米 B.600cos58°米
C.600tan58°米 D.米
5.某燕尾槽示意图如图所示,它是一个轴对称图形,AE=50mm,则燕尾槽的里口宽BC的长为( )
A.(188+50tana)mm B.(188+100tana)mm
C. D.
6.为了解决楼房之间的采光问题,某市有关部门规定:两幢楼之间的最小距离要使中午12时不能遮光.如图,旧楼的一楼窗台高1米,现计划在旧楼正南方向a米处再建一幢新楼.已知该市冬天中午12时太阳从正南方向照射的光线与水平的夹角最小为θ,问新楼房最高可建( )
A.atanθ米 B.(atanθ+1)米
C.米 D.米
二.填空题(共5小题,满分25分)
7.如图,某梯子长10米,斜靠在竖直的墙面上,当梯子与水平地面所成角为α时,梯子顶端靠在墙面上的点B处,底端落在水平地面的点A处,如果将梯子底端向墙面靠近,使梯子与地面所成角为β,且sinα=cosβ=,则梯子顶端上升了 米.
8.一段公路路面的坡度为i=1:2.4,如果某人沿着这段公路向上行走了130米,那么此人升高了 米.
9.如图,为了了解山坡上两棵树间的水平距离,数学活动小组的同学们测得该山坡的倾斜角α=23°,两树间的坡面距离AB=10m,则这两棵树的水平距离约为 m.(结果精确到0.1m,参考数据:sin23°≈0.391,cos23°≈0.921,tan23°≈0.424)
10.小颖家住在甲楼,她所居住的楼房前面有一座乙楼.冬天,阳光入射角是30°,两楼距离20米,小颖家的阳台距地面7米,乙楼高18米,那么影子的顶端距她家阳台还有 米.(精确到0.1米)
11.如图是某水库大坝横断面示意图.其中AB、CD分别表示水库上下底面的水平线,∠ABC=135°,BC的长是40m,则水库大坝的高度h是 m.(结果保留根号)
三.解答题(共9小题,满分65分)
12.避雷针是用来保护建筑物、高大树木等避免雷击的装置.如图,小陶同学要测量垂直于地面的大楼BC顶部避雷针CD的长度(B,C,D三点共线),在水平地面A点测得∠CAB=53°,∠DAB=58°,A点与大楼底部B点的距离AB=20m,求避雷针CD的长度.(结果精确到0.1m.参考数据:sin58°≈0.85,cos58°≈0.53,tan58°≈1.60,sin53°≈0.80,cos53°≈0.60,tan53°≈1.33)
13.学校运动场的四角各有一盏探照灯,其中一盏探照灯B的位置如图所示,已知坡长AC=12m,坡角α为30°,灯光受灯罩的影响,最远端的光线与地面的夹角β为27°,最近端的光线恰好与地面交于坡面的底端C处,且与地面的夹角为60°,A、B、C、D在同一平面上.(结果精确到0.1m.参考数据:sin27°≈0.45,cos27°≈0.89,tan27°≈0.51,≈1.73.)
(1)求灯杆AB的高度;
(2)求CD的长度.
14.图①是一种手机平板支架,由托板、支撑板和底座构成,手机放置在托板上,图②是其侧面结构示意图,托板长AB=115mm,支撑板长CD=70mm,板AB固定在支撑板顶点C处,且CB=35mm,托板AB可绕点C转动,支撑板CD可绕点D转动,∠CDE=60°.
(1)若∠DCB=70°时,求点A到直线DE的距离(计算结果精确到个位);
(2)为了观看舒适,把(1)中∠DCB=70°调整为90°,再将CD绕点D逆时针旋转,使点B落在直线DE上即可,求CD旋转的角度.
(参考数据:sin50°≈0.8,cos50°≈0.6,tan50°≈1.2,sin26.6°≈0.4,cos26.6°≈0.9,tan26.6°≈0.5,≈1.7)
15.如图,为了测量河对岸两点A,B之间的距离,在河岸这边取点C,D.测得CD=80m,∠ACD=90°,∠BCD=45°,∠ADC=19°17′,∠BDC=56°19′.设A,B,C,D在同一平面内,求A,B两点之间的距离.
(参考数据:tan19°17′≈0.35,tan56°19′≈1.50.)
16.如图1是平凉市地标建筑“大明宝塔”,始建于明嘉靖十四年(1535年),是明代平凉韩王府延恩寺的主体建筑.宝塔建造工艺精湛,与崆峒山的凌空塔遥相呼应,被誉为平凉古塔“双璧”.某数学兴趣小组开展了测量“大明宝塔的高度”的实践活动,具体过程如下:
方案设计:如图2,宝塔CD垂直于地面,在地面上选取A,B两处分别测得∠CAD和∠CBD的度数(A,D,B在同一条直线上).
数据收集:通过实地测量:地面上A,B两点的距离为58m,∠CAD=42°,∠CBD=58°.
问题解决:求宝塔CD的高度(结果保留一位小数).
参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90,sin58°≈0.85,cos58°≈0.53,tan58°≈1.60.
根据上述方案及数据,请你完成求解过程.
17.学生到工厂劳动实践,学习制作机械零件.零件的截面如图阴影部分所示,已知四边形AEFD为矩形,点B、C分别在EF、DF上,∠ABC=90°,∠BAD=53°,AB=10cm,BC=6cm.求零件的截面面积.参考数据:sin53°≈0.80,cos53°≈0.60.
18.某一天,小明和小亮想利用所学过的测量知识来测量一棵古树的高度AB.他们带着测量工具来到这棵古树前,由于有围栏保护,他们无法到达古树的底部B,如图所示,于是他们先在古树周围的空地上选择一点D,通过测倾器测的角度为45°,再在BD的延长线上确定一点F,使DF=5米,并在F处通过测倾器测的角度为30°,测倾器的高度CD=EF=1米.已知点F、D、B在同一水平直线上,且EF、CD、AB均垂直于FB,则这棵古树的高度AB为多少米?(结果保留根号)
19.某型号飞机的机翼形状为如图所示的四边形ABDC,已知AB∥CD,∠C=45°,∠ABD=60°,CD长为3.4m.点B到CD的距离BE为5m,请根据以上数据计算AB的长度.
20.如图,地面上小山的两侧有A、B两地,为了测量A、B两地的距离,让一热气球从小山西侧A地出发沿与AB成30°角的方向,以每分钟50m的速度直线飞行,8分钟后到达C处,此时热气球上的人测得CB与AB成70°角,请你用测得的数据求A,B两地的距离AB长.(取1.7,sin20°取0.3,cos20°取0.9,tan20°取0.4,sin70°取0.9,cos70°取0.3,tan70°取2.7.)
参考答案
一.选择题(共6小题,满分30分)
1.解:如图,连接CD,过O作OF⊥CD于点F,延长FO,交AB于点E,
∵OA=OB=OC=OD=20cm,∠COD=60°,
∴∠COF=30°,
∴CF=OC cos∠COF==30(cm),
∴EF=2OF=60(cm),
即点A到地面(CD所在的平面)的距离是60cm.
故选:D.
2.解:过点C、D作DM⊥AB,CN⊥AB,垂足为M、N,
在Rt△BCN中,∠CBN=30°,BC=500m,
∴CN=BC=250(m)=DM,BN=BC=250(m),
在Rt△ADM中,∠DAM=45°,DM=250m,
∴AM=DM=250m,
∴AB=AM+MN+BN=250+50+250=(300+250)m,
故选:C.
3.解:∵PA⊥PB,
∴∠APC=90°,
∵PC=50米,∠PCA=44°,
∴tan44°=,
∴小河宽PA=PCtan∠PCA=50 tan44°(米).
故选:C.
4.解:∵∠DBE=180°﹣∠ABD=180°﹣148°=32°,
∴∠E=180°﹣32°﹣58°=90°,
∴△BDE是直角三角形,
∵BD=600米,cos∠D=,
∴开挖点E离点D的距离DE=600cos58°米.
故选:B.
5.解:如图,作AE⊥BC于点E,DF⊥BC于点F,
∵燕尾槽是一个轴对称图形,
∴∠B=∠C=α,AP=DQ=56mm,
∴EF=AD=300﹣112=188mm,
∴Rt△ABE中,BE==mm,
同理可得CF==mm,
∴BC=BE+EF+CF=(188+)mm.
故选:D.
6.解:如图,过点D作DE⊥AB与点E,
在Rt△ADE中,∠ADE=θ,DE=BC=a米,
则AE=tanθ DE=atanθ,
而EB=DC=1米,
∴AB=AE+EB=(atanθ+1)(米),
答:新楼房最高可建(atanθ+1)米,
故选:B.
二.填空题(共5小题,满分25分)
7.解:如图,由题意可知,∠ACB=90°,AB=ED=10,
由=sinα==cosβ=,
设BC=3m,则AB=5m,
则5m=10,
解得m=2,
∴BC=3×2=6,
设EC=3n,则ED=5n,
∴5n=10,
解得n=2,
∴EC=3×2=6,
∴DC===8,
∴BD=DC﹣BC=8﹣6=2(米),
∴梯子顶端上升了2米,
故答案为:2.
8.解:设此人升高了x米,
∵坡比为1:2.4,
∴他行走的水平宽度为2.4x米,
由勾股定理得,x2+(2.4x)2=1302,
解得,x=50,即他沿着垂直方向升高了50米,
故答案为:50.
9.解:过点A作水平面的平行线AC,过点B作BC⊥AC于C,
由题意得:AB=10m,∠BAC=23°,
则AC=AB cos∠BAC≈10×0.921≈9.2(米),
故答案为:9.2.
10.解:如图,
在Rt△ABC中,∠ABC=90°,∠ACB=30°,BC=20m,
∴AB=BC×tan30°=m≈11.55m,
CD=18﹣11.55=6.45m,
∴影子的顶端距她家的阳台还有7﹣6.45=0.55≈0.6m.
故答案为:0.6m.
11.解:如图,作CH⊥AB于点H.
∵∠ABC=135°,
∴∠CBH=45°,
∴CH=BC sin45°=40×=20(m),
故答案为:20.
三.解答题(共9小题,满分65分)
12.解:在Rt△ABD中,∵tan∠BAD=,
∴1.60=,
∴BD=32(米),
在Rt△CAD中,∵tan∠CAD=,
∴1.33=,
∴CD=26.6(米),
∴CD=BC﹣BD=5.4(米).
答:避雷针DC的长度为5.4米.
13.解:(1)延长BA交CG于点E,
则BE⊥CG,
在Rt△ACE中,∠ACE=30°,AC=12m,
∴AE=AC=×12=6(m),CE=AC cosα=12×=6(m),
在Rt△BCE中,∠BCE=60°,
∴BE=CE tan∠BCE=6×=18(m),
∴AB=BE﹣AE=18﹣6=12(m);
(2)在Rt△BDE中,∠BDE=27°,
∴CD=DE﹣CE=﹣6≈24.9(m).
14.解:(1)过点C作CG∥DE,过点A作AH⊥CG于H,过点C作CF⊥DE于点F,
则点A到直线DE的距离为:AH+CF.
在Rt△CDF中,
∵sin∠CDE=,
∴CF=CD sin60°=70×=35≈59.5(mm).
∵∠DCB=70°,
∴∠ACD=180°﹣∠DCB=110°,
∵CG∥DE,
∴∠GCD=∠CDE=60°.
∴∠ACH=∠ACD﹣∠DCG=50°.
在Rt△ACH中,
∵sin∠ACH=,
∴AH=AC sin∠ACH=(115﹣35)×sin50°≈80×0.8=64(mm).
∴点A到直线DE的距离为AH+CF=59.5+64=123.5≈124(mm).
(2)如下图所示,虚线部分为旋转后的位置,B的对应点为B′,C的对应点为C′,
则B′C′=BC=35 mm,DC′=DC=70 mm.
在Rt△B′C′D中,
∵tan∠B′DC′==0.5,tan26.6°≈0.5,
∴∠B′DC′=26.6°.
∴CD旋转的角度为∠CDC′=∠CDE﹣∠B′DC′=60°﹣26.6°=33.4°.
15.解:过B作BE⊥CD于E,过A作AF⊥BE于F,如图:
∵∠BCD=45°,
∴△BCE是等腰直角三角形,
设CE=x,则BE=x,
∵CD=80m,
∴DE=(80﹣x)m,
Rt△BDE中,∠BDC=56°19',
∴tan56°19'=,即=1.5,
解得x=48(m),
∴BE=CE=48m,
Rt△ACD中,∠ADC=19°17′,CD=80m,
∴tan19°17'=,即=0.35,
解得AC=28m,
∵∠ACD=90°,BE⊥CD于E,AF⊥BE,
∴四边形ACEF是矩形,
∴AF=CE=48m,EF=AC=28m,
∴BF=BE﹣EF=20m,
Rt△ABF中,AB===52(m),
答:A,B两点之间的距离是52m.
16.解:设CD=xm,
在Rt△ACD中,AD=,
在Rt△BCD中,BD=,
∵AD+BD=AB,
∴,
解得,x≈33.4.
答:宝塔的高度约为33.4m.
17.解:如图,
∵四边形AEFD为矩形,∠BAD=53°,
∴AD∥EF,∠E=∠F=90°,
∴∠BAD=∠EBA=53°,
在Rt△ABE中,∠E=90°,AB=10cm,∠EBA=53°,
∴sin∠EBA=≈0.80,cos∠EBA=≈0.60,
∴AE=8cm,BE=6cm,
∵∠ABC=90°,
∴∠FBC=90°﹣∠EBA=37°,
∴∠BCF=90°﹣∠FBC=53°,
在Rt△BCF中,∠F=90°,BC=6cm,
∴sin∠BCF=≈0.80,cos∠BCF=≈0.60,
∴BF=4.8cm,FC=3.6cm,
∴EF=6+4.8=10.8cm,
∴S四边形EFDA=AE EF=8×10.8=86.4(cm2),
S△ABE==×8×6=24(cm2),
S△BCF= BF CF=×4.8×3.6=8.64(cm2),
∴截面的面积=S四边形EFDA﹣S△ABE﹣S△BCF=86.4﹣24﹣8.64=53.76(cm2).
18.解:连接EC并延长交AB于点N,
由题意可得:EN⊥AB,四边形EFDC是矩形,
故FD=EC=5米,EF=DC=BN=1米,
则设AN=x米,故CN=x米,
可得:tan30°=,
解得:x=,
则AB=+1=(米),
答:这棵古树的高度AB为米.
19.解:由题意得BE⊥CE,过A作AH⊥CD于H,
则AH=BE=5m,EH=AB,
∵∠AHC=90°,∠C=45°,
∴CH=AH=5(m),
∴DH=CH﹣CD=5﹣3.4=1.6(m),
在Rt△BDE中,∵∠ABE=90°,∠ABD=60°,
∴∠DBE=30°,
∵BE=5,
∴DE=BE=×5=,
∴AB=HE=DE﹣DH=﹣1.6=.
20.解:过点C作CM⊥AB交AB延长线于点M,
由题意得:AC=50×8=400(m),
在Rt△ACM中,
∵∠A=30°,
∴CM=AC=200(m),AM=AC cos∠A=400×=200(m),
在Rt△BCM中,
∵∠CBM=70°,
∴∠BCM=20°,
∵tan20°=,
∴BM=200tan20°,
∴AB=AM﹣BM=200﹣200tan20°=200(﹣tan20°)=200(1.7﹣0.4)=260(m),
因此A,B两地的距离AB长为260m.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
