人教版2021-2022学年八年级数学上册14.2乘法公式知识点分类练习题 (word版、含答案)
文档属性
| 名称 | 人教版2021-2022学年八年级数学上册14.2乘法公式知识点分类练习题 (word版、含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 197.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-28 00:00:00 | ||
图片预览




文档简介
2021-2022学年人教版八年级数学上册《14.2乘法公式》知识点分类练习题(附答案)
一.平方差公式
1.(3+1)×(32+1)×(34+1)×……×(332+1)+的值为 .
2.已知a2﹣4b2=12,且a﹣2b=﹣3,则a+b= .
3.计算:9992﹣1002×998+1= .
4.已知:a﹣b=1,a2﹣b2=﹣1,那么3a2008﹣5b2008= .
5.(3x+2y)2﹣(3x﹣2y)2= .
6.计算
(1);
(2)(xm﹣yn)(xm+yn);
(3);
(4)(x+y+z)2.
7.简便计算:
(1)20232﹣2024×2022;
(2)2982;
(3);
(4)99.82.
8.(3x﹣2y)2﹣(3x+2y)2
9.计算:(2a﹣b+c)(b﹣2a﹣c)
二.平方差公式的几何背景
10.如图:边长为a,b的两个正方形,边保持平行,如果从大正方形中剪去小正方形,剩下的图形可以分割成4个大小相等的梯形.请你计算出两个阴影部分的面积,同时说明可以验证哪一个乘法公式的几何意义.
三.完全平方公式
11.若关于x的多项式x2+ax+9是完全平方式,则a= .
12.关于x的二次多项式x2+6x+m恰好是另一个多项式的平方,则常数项m= .
13.a2x2﹣4x+b2是一个完全平方式,则ab= .
14.若a+b=,a﹣b=,则ab= .
15.已知(a+b)2=9,ab=﹣,则a2+b2的值等于 .
16.若x满足(2021﹣x)2+(x﹣2020)2=2019,则(2021﹣x)(x﹣2020)的值是( )
A.﹣1006 B.﹣1007 C.﹣1008 D.﹣1009
17.化简(x+y+z)2﹣(﹣x+y+z)2+(x﹣y+z)2﹣(x+y﹣z)2的结果是( )
A.4yz B.8xy C.4xy﹣4yz D.8xz
18.已知x满足(x﹣2014)2+(2016﹣x)2=8,则(x﹣2015)2的值是 .
19.若a+2b+3c=12,且a2+b2+c2=ab+bc+ca,则a+b2+c3= .
20.若(a+b)2=16,a2﹣b2=12,则ab= .
21.若xy=1,x﹣y=﹣4,则x2+3xy+y2= .
22.已知(a﹣2b)2=9,(a+2b)2=25,则a2+4b2= .
23.设(5a+3b)2=(5a﹣3b)2+A,则A= .
24.已知:a+2b=5,2b﹣c=7,则代数式a2+2ac+c2的值是 .
25.( ﹣b2)2= ﹣a3b2+ .
26.已知a+b+c=m,a2+b2+c2=n,则ab+bc+ca= .
27.若a=1990,b=1991,c=1992,则a2+b2+c2﹣ab﹣bc﹣ca= .
28.x2+y2=(x+y)2+P=(x﹣y)2+Q,则P= ,Q= .
四.完全平方公式的几何背景
29.如图,两个正方形边长分别为a、b,如果a+b=18,ab=12,则阴影部分的面积为 .
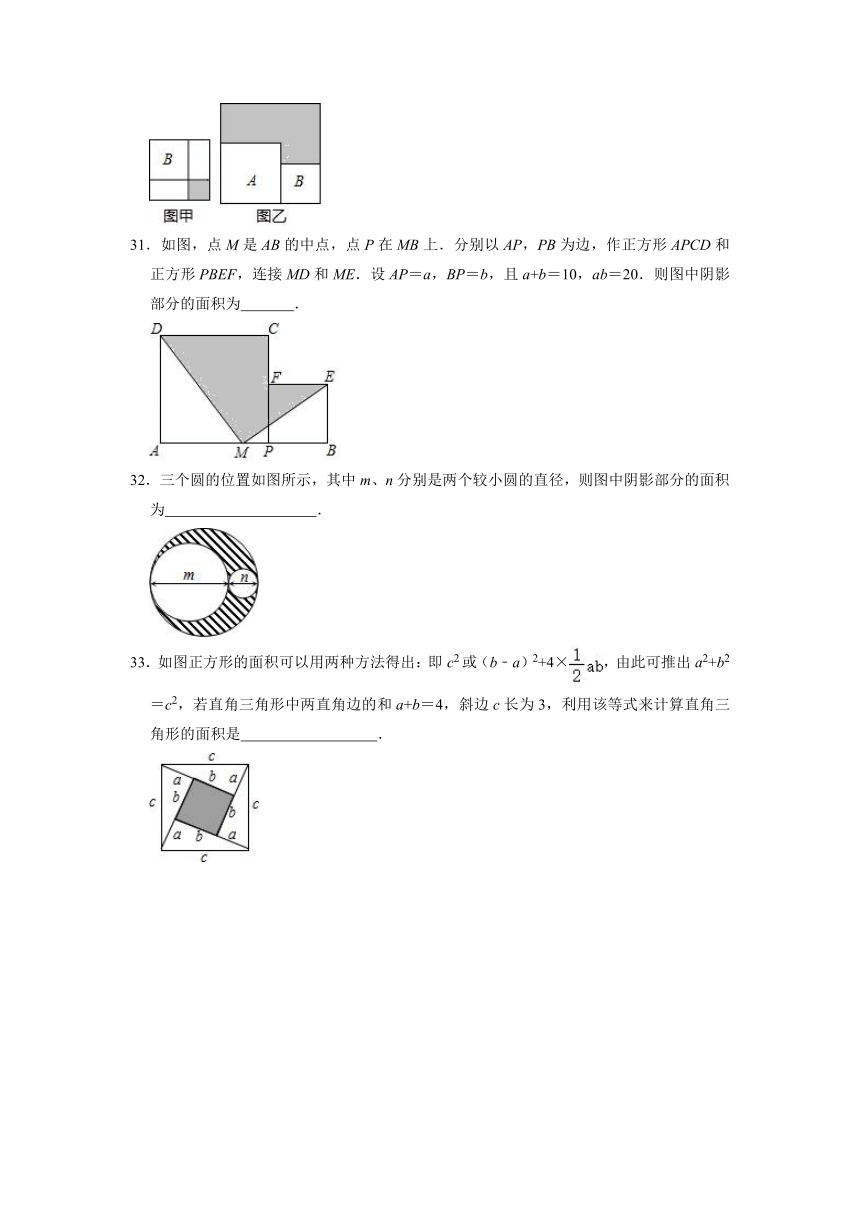
30.有两个正方形A,B,现将B放在A的内部得图甲,将A,B并列放置后构造新的正方形得图乙.若图甲和图乙中阴影部分的面积分别为1和12,则正方形A,B的边长之和为 .
31.如图,点M是AB的中点,点P在MB上.分别以AP,PB为边,作正方形APCD和正方形PBEF,连接MD和ME.设AP=a,BP=b,且a+b=10,ab=20.则图中阴影部分的面积为 .
32.三个圆的位置如图所示,其中m、n分别是两个较小圆的直径,则图中阴影部分的面积为 .
33.如图正方形的面积可以用两种方法得出:即c2或(b﹣a)2+4×,由此可推出a2+b2=c2,若直角三角形中两直角边的和a+b=4,斜边c长为3,利用该等式来计算直角三角形的面积是 .
参考答案
一.平方差公式
1.解:原式=(3﹣1)×(3+1)×(32+1)×(34+1)×……×(332+1)+
=(32﹣1)×(32+1)×(34+1)×……×(332+1)+
=(34﹣1)×(34+1)×……×(332+1)+
=(38﹣1)×……×(332+1)+
=(364﹣1)+
=﹣+
=.
2.解:∵a2﹣4b2=(a+2b)(a﹣2b)=12,a﹣2b=﹣3,
∴﹣3(a+2b)=12,
a+2b=﹣4,
联立a﹣2b=﹣3,
可得2a=﹣7,解得a=﹣3.5,
把a=﹣3.5代入a+2b=﹣4得﹣3.5+2b=﹣4,解得b=﹣0.25,
则a+b=﹣3.5﹣0.25=﹣3.75.
故答案为:﹣3.75.
3.解:原式=(1000﹣1)2﹣(1000﹣2)×(1000+2)+1,
=10002﹣2000+1﹣10002+4+1,
=﹣1994
故答案是:﹣1994..
4.解:∵a﹣b=1,a2﹣b2=﹣1,
∴(a+b)(a﹣b)=﹣1,
∴a+b=﹣1,
∵a﹣b=1,
解得:a=0,b=﹣1,
∴3a2008﹣5b2008=3×0﹣5×1=﹣5,
故答案为:﹣5.
5.解:(3x+2y)2﹣(3x﹣2y)2,
=(3x+2y+3x﹣2y)(3x+2y﹣3x+2y),
=6x 4y,
=24xy;
故填24xy.
6.解:(1)原式=(﹣2x2)2﹣()2=4x4﹣;
(2)原式=(xm)2﹣(yn)2=x2m﹣y2n;
(3)原式=[(a+b)(a﹣b)]2,
=(a2﹣b2)2,
=;
(4)(x+y+z)2,
=(x+y)2+2(x+y)z+z2,
=x2+2xy+y2+2yz+2xz+z2,
=x2+y2+z2+2xy+2yz+2xz.
7.解:(1)原式=20232﹣(2023+1)(2023﹣1)
=20232﹣(20232﹣1)
=1;
(2)原式=2982﹣22+4=(298+2)(298﹣2)+4
=300×296+4
=88800+4
=88804;
(3)原式=(10﹣)(10+)
=102﹣()2
=100﹣
=;
(4)原式=(100﹣0.2)2
=1002﹣2×100×0.4+0.22=10000﹣40+0.04
=9960.04.
8.解:(3x﹣2y)2﹣(3x+2y)2,
=[(3x﹣2y)+(3x+2y)][(3x﹣2y)﹣(3x+2y)],
=(3x﹣2y+3x+2y)(3x﹣2y﹣3x﹣2y),
=6x (﹣4y)=﹣24xy.
9.解:(2a﹣b+c)(b﹣2a﹣c)=﹣[(2a+c)﹣b][(2a+c)+b]=﹣(2a+c)2+b2=﹣4a2﹣4ac﹣c2+b2.
二.平方差公式的几何背景
10.解:∵第一个图形的阴影部分的面积是a2﹣b2,第二个图形的阴影部分的面积是(a+b)(a﹣b),
∴a2﹣b2=(a+b)(a﹣b).
即可以验证平方差公式的几何意义.
三.完全平方公式
11.解:∵关于x的多项式x2+ax+9是完全平方式,
∴a=±6,
故答案为:±6
12.解:∵二次多项式x2+6x+m恰好是另一个多项式的平方,
∴m=9.
故答案为:9
13.解:中间一项为加上或减去ax和b积的2倍,
故±2ab=﹣4,
ab=±2
故填±2.
14.解:方法1:∵a+b=,a﹣b=,
∴(a+b)2=7,(a﹣b)2=3,
∴a2+2ab+b2=7,a2﹣2ab+b2=3,
4ab=4,
ab=1;
方法2:将a+b=,a﹣b=两式相加得:2a=+,即a=,
将a=5代入a﹣b=中,得:﹣b=,即b=,
则ab==1.
故答案为:1.
15.解:当(a+b)2=9,ab=﹣时,
a2+b2=(a+b)2﹣2ab
=9﹣2×(﹣)
=12,
故答案为:12.
16.解:设2021﹣x=a,x﹣2020=b,则(2021﹣x)2+(x﹣2020)2=a2+b2=2019,a+b=(2021﹣x)+(x﹣2020)=1,
所以,(2021﹣x)(x﹣2020)=ab=[(a+b)2﹣(a2+b2)]=×(12﹣2019)=﹣1009;
故选:D.
17.解:(x+y+z)2﹣(﹣x+y+z)2+(x﹣y+z)2﹣(x+y﹣z)2
=(x+y+z﹣x+y+z)(x+y+z+x﹣y﹣z)+(x﹣y+z+x+y﹣z)(x﹣y+z﹣x﹣y+z)
=2(y+z)×2x+2x×2(z﹣y)
=4xy+4xz+4xz﹣4xy
=8xz,
故选:D.
18.解:方程(x﹣2014)2+(2016﹣x)2=8可变形为:
[(x﹣2015)+1]2+[(x﹣2015﹣1)]2=8
设x﹣2015=y
则原方程可转化为:(y+1)2+(y﹣1)2=8
∴y2+2y+1+y2﹣2y+1=8
即2y2=6
∴y2=3
即(x﹣2015)2=3.
故答案为:3.
19.解:∵a2+b2+c2=ab+bc+ca,
∴2(a2+b2+c2)=2(ab+bc+ca),
即2(a2+b2+c2)﹣2(ab+bc+ca)=0,
整理,得(a2﹣2ab+b2)+(a2﹣2ca+c2)+(b2﹣2bc+c2)=0,
即:(a﹣b)2+(a﹣c)2+(b﹣c)2=0,
∴a=b=c,
又∵a+2b+3c=12,
∴a=b=c=2.
∴a+b2+c3=2+4+8=14.
20.解:a2﹣b2=12,
(a+b)2(a﹣b)2=144,
将(a+b)2=16代入得(a﹣b)2=9,
(a+b)2=16与(a﹣b)2=9左右分别相减得4ab=7,
解得ab=.
故答案为:.
21.解:∵xy=1,x﹣y=﹣4,
∴x2+3xy+y2=(x﹣y)2+5xy=(﹣4)2+5×1=16+5=21.
故答案是:21.
22.解:∵(a﹣2b)2=9,(a+2b)2=25,
相加得到a2+4ab+4b2+a2﹣4ab+4b2=34,即2a2+8b2=34,
∴a2+4b2=17.
故答案为:17.
23.解:∵(5a+3b)2=(5a﹣3b)2+A,
∴25a2+9b2+30ab=25a2+9b2﹣30ab+A,
∴A=60ab.
故答案为:60ab.
24.解:∵a+2b=5,2b﹣c=7,
∴a+c=5﹣7=﹣2,
∴a2+2ac+c2,
=(a+c)2,
=(﹣2)2,
=4.
25.解:(a3﹣b2)2=a6﹣a3b2+b4.
26.解:∵a+b+c=m,a2+b2+c2=n,
∴(a+b+c)2=m2,
即a2+b2+c2+2ab+2ac+2bc=m2,
∴ab+ac+ab=[m2﹣(a2+b2+c2)]=(m2﹣n).
27.解:因为a=1990,b=1991,c=1992,所以
a2+b2+c2﹣ab﹣bc﹣ca=(2a2+2b2+2c2﹣2ab﹣2bc﹣2ca),
=[(a2﹣2ab+b2)+(b2﹣2bc+c2)+(c2﹣2ca+a2)],
=[(a﹣b)2+(b﹣c)2+(c﹣a)2],
=[(1990﹣1991)2+(1991﹣1992)2+(1992﹣1990)2],
=[(﹣1)2+(﹣1)2+(+2)2],
=3.
28.解:x2+y2=(x+y)2﹣2xy=(x﹣y)2+2xy,故答案为﹣2xy、2xy.
四.完全平方公式的几何背景
29.解:阴影部分的面积为:
S正方形ABCD+S正方形CEFG﹣S△ABD﹣S△BFG
=
=
=
=
=.
∵a+b=18,ab=12,
∴阴影部分的面积为:=144.
∴阴影部分的面积为 144.
故答案为:144.
30.解:设正方形A,B的边长分别为a,b.
由题意
由②得到ab=6,
∴(a+b)2=(a﹣b)2+4ab=1+24=25,
∵a+b>0,
∴a+b=5,
故答案为5.
31.解:∵AP=a,BP=b,点M是AB的中点,
∴AM=BM=,
∴S阴影=S正方形APCD+S正方形BEFP﹣S△ADM﹣S△BEM
=a2+b2﹣a×﹣b×
=a2+b2﹣(a+b)2
=(a+b)2﹣2ab﹣(a+b)2
=100﹣40﹣25
=35,
故答案为:35.
32.解:由题意,得
π()2﹣π()2﹣π()2
=mnπ,
故答案为:mnπ.
33.解:∵a2+b2=c2,
∴(a+b)2﹣2ab=c2,
又∵a+b=4,斜边c长为3,
∴42﹣2ab=32,
∴ab=,
∴直角三角形的面积为ab=,
故答案为:.
一.平方差公式
1.(3+1)×(32+1)×(34+1)×……×(332+1)+的值为 .
2.已知a2﹣4b2=12,且a﹣2b=﹣3,则a+b= .
3.计算:9992﹣1002×998+1= .
4.已知:a﹣b=1,a2﹣b2=﹣1,那么3a2008﹣5b2008= .
5.(3x+2y)2﹣(3x﹣2y)2= .
6.计算
(1);
(2)(xm﹣yn)(xm+yn);
(3);
(4)(x+y+z)2.
7.简便计算:
(1)20232﹣2024×2022;
(2)2982;
(3);
(4)99.82.
8.(3x﹣2y)2﹣(3x+2y)2
9.计算:(2a﹣b+c)(b﹣2a﹣c)
二.平方差公式的几何背景
10.如图:边长为a,b的两个正方形,边保持平行,如果从大正方形中剪去小正方形,剩下的图形可以分割成4个大小相等的梯形.请你计算出两个阴影部分的面积,同时说明可以验证哪一个乘法公式的几何意义.
三.完全平方公式
11.若关于x的多项式x2+ax+9是完全平方式,则a= .
12.关于x的二次多项式x2+6x+m恰好是另一个多项式的平方,则常数项m= .
13.a2x2﹣4x+b2是一个完全平方式,则ab= .
14.若a+b=,a﹣b=,则ab= .
15.已知(a+b)2=9,ab=﹣,则a2+b2的值等于 .
16.若x满足(2021﹣x)2+(x﹣2020)2=2019,则(2021﹣x)(x﹣2020)的值是( )
A.﹣1006 B.﹣1007 C.﹣1008 D.﹣1009
17.化简(x+y+z)2﹣(﹣x+y+z)2+(x﹣y+z)2﹣(x+y﹣z)2的结果是( )
A.4yz B.8xy C.4xy﹣4yz D.8xz
18.已知x满足(x﹣2014)2+(2016﹣x)2=8,则(x﹣2015)2的值是 .
19.若a+2b+3c=12,且a2+b2+c2=ab+bc+ca,则a+b2+c3= .
20.若(a+b)2=16,a2﹣b2=12,则ab= .
21.若xy=1,x﹣y=﹣4,则x2+3xy+y2= .
22.已知(a﹣2b)2=9,(a+2b)2=25,则a2+4b2= .
23.设(5a+3b)2=(5a﹣3b)2+A,则A= .
24.已知:a+2b=5,2b﹣c=7,则代数式a2+2ac+c2的值是 .
25.( ﹣b2)2= ﹣a3b2+ .
26.已知a+b+c=m,a2+b2+c2=n,则ab+bc+ca= .
27.若a=1990,b=1991,c=1992,则a2+b2+c2﹣ab﹣bc﹣ca= .
28.x2+y2=(x+y)2+P=(x﹣y)2+Q,则P= ,Q= .
四.完全平方公式的几何背景
29.如图,两个正方形边长分别为a、b,如果a+b=18,ab=12,则阴影部分的面积为 .
30.有两个正方形A,B,现将B放在A的内部得图甲,将A,B并列放置后构造新的正方形得图乙.若图甲和图乙中阴影部分的面积分别为1和12,则正方形A,B的边长之和为 .
31.如图,点M是AB的中点,点P在MB上.分别以AP,PB为边,作正方形APCD和正方形PBEF,连接MD和ME.设AP=a,BP=b,且a+b=10,ab=20.则图中阴影部分的面积为 .
32.三个圆的位置如图所示,其中m、n分别是两个较小圆的直径,则图中阴影部分的面积为 .
33.如图正方形的面积可以用两种方法得出:即c2或(b﹣a)2+4×,由此可推出a2+b2=c2,若直角三角形中两直角边的和a+b=4,斜边c长为3,利用该等式来计算直角三角形的面积是 .
参考答案
一.平方差公式
1.解:原式=(3﹣1)×(3+1)×(32+1)×(34+1)×……×(332+1)+
=(32﹣1)×(32+1)×(34+1)×……×(332+1)+
=(34﹣1)×(34+1)×……×(332+1)+
=(38﹣1)×……×(332+1)+
=(364﹣1)+
=﹣+
=.
2.解:∵a2﹣4b2=(a+2b)(a﹣2b)=12,a﹣2b=﹣3,
∴﹣3(a+2b)=12,
a+2b=﹣4,
联立a﹣2b=﹣3,
可得2a=﹣7,解得a=﹣3.5,
把a=﹣3.5代入a+2b=﹣4得﹣3.5+2b=﹣4,解得b=﹣0.25,
则a+b=﹣3.5﹣0.25=﹣3.75.
故答案为:﹣3.75.
3.解:原式=(1000﹣1)2﹣(1000﹣2)×(1000+2)+1,
=10002﹣2000+1﹣10002+4+1,
=﹣1994
故答案是:﹣1994..
4.解:∵a﹣b=1,a2﹣b2=﹣1,
∴(a+b)(a﹣b)=﹣1,
∴a+b=﹣1,
∵a﹣b=1,
解得:a=0,b=﹣1,
∴3a2008﹣5b2008=3×0﹣5×1=﹣5,
故答案为:﹣5.
5.解:(3x+2y)2﹣(3x﹣2y)2,
=(3x+2y+3x﹣2y)(3x+2y﹣3x+2y),
=6x 4y,
=24xy;
故填24xy.
6.解:(1)原式=(﹣2x2)2﹣()2=4x4﹣;
(2)原式=(xm)2﹣(yn)2=x2m﹣y2n;
(3)原式=[(a+b)(a﹣b)]2,
=(a2﹣b2)2,
=;
(4)(x+y+z)2,
=(x+y)2+2(x+y)z+z2,
=x2+2xy+y2+2yz+2xz+z2,
=x2+y2+z2+2xy+2yz+2xz.
7.解:(1)原式=20232﹣(2023+1)(2023﹣1)
=20232﹣(20232﹣1)
=1;
(2)原式=2982﹣22+4=(298+2)(298﹣2)+4
=300×296+4
=88800+4
=88804;
(3)原式=(10﹣)(10+)
=102﹣()2
=100﹣
=;
(4)原式=(100﹣0.2)2
=1002﹣2×100×0.4+0.22=10000﹣40+0.04
=9960.04.
8.解:(3x﹣2y)2﹣(3x+2y)2,
=[(3x﹣2y)+(3x+2y)][(3x﹣2y)﹣(3x+2y)],
=(3x﹣2y+3x+2y)(3x﹣2y﹣3x﹣2y),
=6x (﹣4y)=﹣24xy.
9.解:(2a﹣b+c)(b﹣2a﹣c)=﹣[(2a+c)﹣b][(2a+c)+b]=﹣(2a+c)2+b2=﹣4a2﹣4ac﹣c2+b2.
二.平方差公式的几何背景
10.解:∵第一个图形的阴影部分的面积是a2﹣b2,第二个图形的阴影部分的面积是(a+b)(a﹣b),
∴a2﹣b2=(a+b)(a﹣b).
即可以验证平方差公式的几何意义.
三.完全平方公式
11.解:∵关于x的多项式x2+ax+9是完全平方式,
∴a=±6,
故答案为:±6
12.解:∵二次多项式x2+6x+m恰好是另一个多项式的平方,
∴m=9.
故答案为:9
13.解:中间一项为加上或减去ax和b积的2倍,
故±2ab=﹣4,
ab=±2
故填±2.
14.解:方法1:∵a+b=,a﹣b=,
∴(a+b)2=7,(a﹣b)2=3,
∴a2+2ab+b2=7,a2﹣2ab+b2=3,
4ab=4,
ab=1;
方法2:将a+b=,a﹣b=两式相加得:2a=+,即a=,
将a=5代入a﹣b=中,得:﹣b=,即b=,
则ab==1.
故答案为:1.
15.解:当(a+b)2=9,ab=﹣时,
a2+b2=(a+b)2﹣2ab
=9﹣2×(﹣)
=12,
故答案为:12.
16.解:设2021﹣x=a,x﹣2020=b,则(2021﹣x)2+(x﹣2020)2=a2+b2=2019,a+b=(2021﹣x)+(x﹣2020)=1,
所以,(2021﹣x)(x﹣2020)=ab=[(a+b)2﹣(a2+b2)]=×(12﹣2019)=﹣1009;
故选:D.
17.解:(x+y+z)2﹣(﹣x+y+z)2+(x﹣y+z)2﹣(x+y﹣z)2
=(x+y+z﹣x+y+z)(x+y+z+x﹣y﹣z)+(x﹣y+z+x+y﹣z)(x﹣y+z﹣x﹣y+z)
=2(y+z)×2x+2x×2(z﹣y)
=4xy+4xz+4xz﹣4xy
=8xz,
故选:D.
18.解:方程(x﹣2014)2+(2016﹣x)2=8可变形为:
[(x﹣2015)+1]2+[(x﹣2015﹣1)]2=8
设x﹣2015=y
则原方程可转化为:(y+1)2+(y﹣1)2=8
∴y2+2y+1+y2﹣2y+1=8
即2y2=6
∴y2=3
即(x﹣2015)2=3.
故答案为:3.
19.解:∵a2+b2+c2=ab+bc+ca,
∴2(a2+b2+c2)=2(ab+bc+ca),
即2(a2+b2+c2)﹣2(ab+bc+ca)=0,
整理,得(a2﹣2ab+b2)+(a2﹣2ca+c2)+(b2﹣2bc+c2)=0,
即:(a﹣b)2+(a﹣c)2+(b﹣c)2=0,
∴a=b=c,
又∵a+2b+3c=12,
∴a=b=c=2.
∴a+b2+c3=2+4+8=14.
20.解:a2﹣b2=12,
(a+b)2(a﹣b)2=144,
将(a+b)2=16代入得(a﹣b)2=9,
(a+b)2=16与(a﹣b)2=9左右分别相减得4ab=7,
解得ab=.
故答案为:.
21.解:∵xy=1,x﹣y=﹣4,
∴x2+3xy+y2=(x﹣y)2+5xy=(﹣4)2+5×1=16+5=21.
故答案是:21.
22.解:∵(a﹣2b)2=9,(a+2b)2=25,
相加得到a2+4ab+4b2+a2﹣4ab+4b2=34,即2a2+8b2=34,
∴a2+4b2=17.
故答案为:17.
23.解:∵(5a+3b)2=(5a﹣3b)2+A,
∴25a2+9b2+30ab=25a2+9b2﹣30ab+A,
∴A=60ab.
故答案为:60ab.
24.解:∵a+2b=5,2b﹣c=7,
∴a+c=5﹣7=﹣2,
∴a2+2ac+c2,
=(a+c)2,
=(﹣2)2,
=4.
25.解:(a3﹣b2)2=a6﹣a3b2+b4.
26.解:∵a+b+c=m,a2+b2+c2=n,
∴(a+b+c)2=m2,
即a2+b2+c2+2ab+2ac+2bc=m2,
∴ab+ac+ab=[m2﹣(a2+b2+c2)]=(m2﹣n).
27.解:因为a=1990,b=1991,c=1992,所以
a2+b2+c2﹣ab﹣bc﹣ca=(2a2+2b2+2c2﹣2ab﹣2bc﹣2ca),
=[(a2﹣2ab+b2)+(b2﹣2bc+c2)+(c2﹣2ca+a2)],
=[(a﹣b)2+(b﹣c)2+(c﹣a)2],
=[(1990﹣1991)2+(1991﹣1992)2+(1992﹣1990)2],
=[(﹣1)2+(﹣1)2+(+2)2],
=3.
28.解:x2+y2=(x+y)2﹣2xy=(x﹣y)2+2xy,故答案为﹣2xy、2xy.
四.完全平方公式的几何背景
29.解:阴影部分的面积为:
S正方形ABCD+S正方形CEFG﹣S△ABD﹣S△BFG
=
=
=
=
=.
∵a+b=18,ab=12,
∴阴影部分的面积为:=144.
∴阴影部分的面积为 144.
故答案为:144.
30.解:设正方形A,B的边长分别为a,b.
由题意
由②得到ab=6,
∴(a+b)2=(a﹣b)2+4ab=1+24=25,
∵a+b>0,
∴a+b=5,
故答案为5.
31.解:∵AP=a,BP=b,点M是AB的中点,
∴AM=BM=,
∴S阴影=S正方形APCD+S正方形BEFP﹣S△ADM﹣S△BEM
=a2+b2﹣a×﹣b×
=a2+b2﹣(a+b)2
=(a+b)2﹣2ab﹣(a+b)2
=100﹣40﹣25
=35,
故答案为:35.
32.解:由题意,得
π()2﹣π()2﹣π()2
=mnπ,
故答案为:mnπ.
33.解:∵a2+b2=c2,
∴(a+b)2﹣2ab=c2,
又∵a+b=4,斜边c长为3,
∴42﹣2ab=32,
∴ab=,
∴直角三角形的面积为ab=,
故答案为:.
