2021-2022学年冀教版九年级数学下册29.1点与圆的位置关系同步练习题(Word版,附答案解析)
文档属性
| 名称 | 2021-2022学年冀教版九年级数学下册29.1点与圆的位置关系同步练习题(Word版,附答案解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 146.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-28 00:00:00 | ||
图片预览

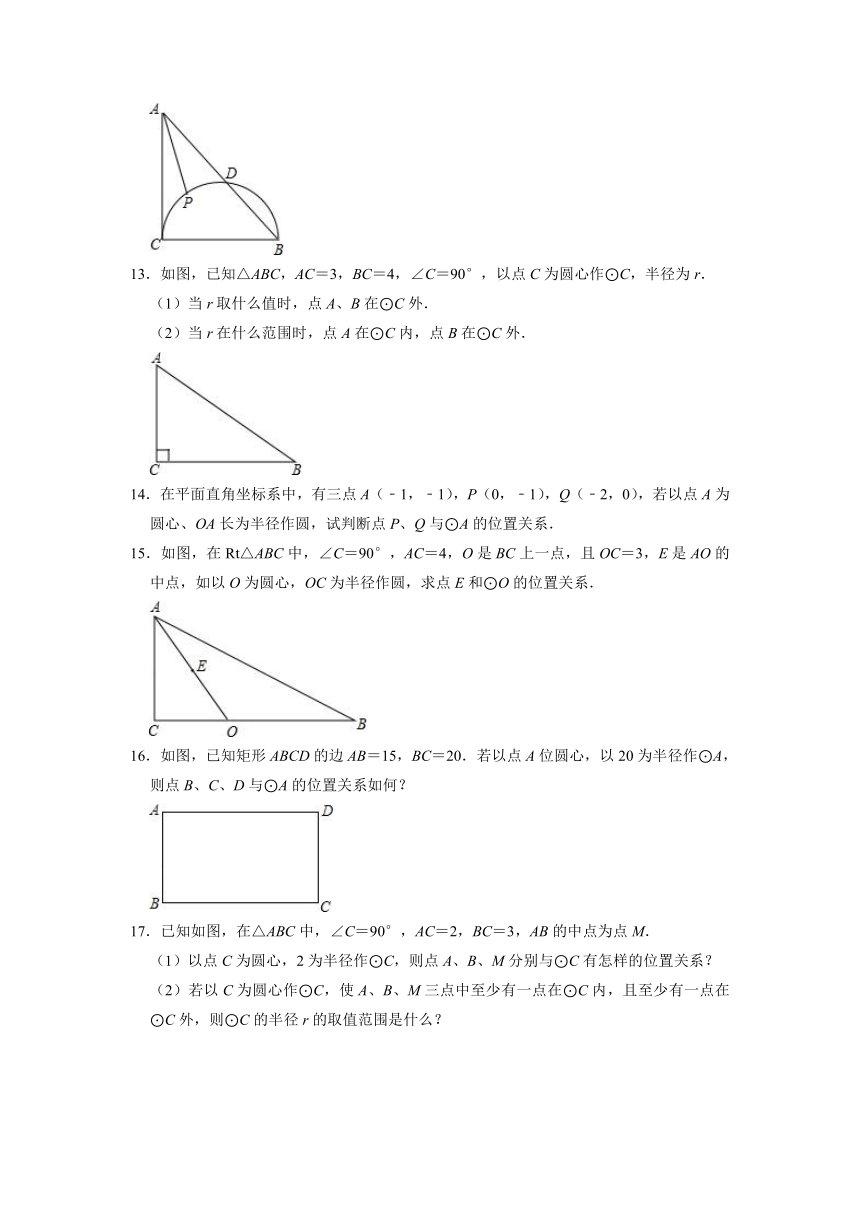
文档简介
2021-2022学年冀教版九年级数学下册《29.1点与圆的位置关系》同步练习题(附答案)
1.若⊙O的半径为5cm,OA=4cm,则点A与⊙O的位置关系是( )
A.点A在⊙O内 B.点A在⊙O上 C.点A在⊙O外 D.内含
2.已知⊙O的半径为4cm,点A到圆心O的距离为3cm,则点A与⊙O的位置关系是( )
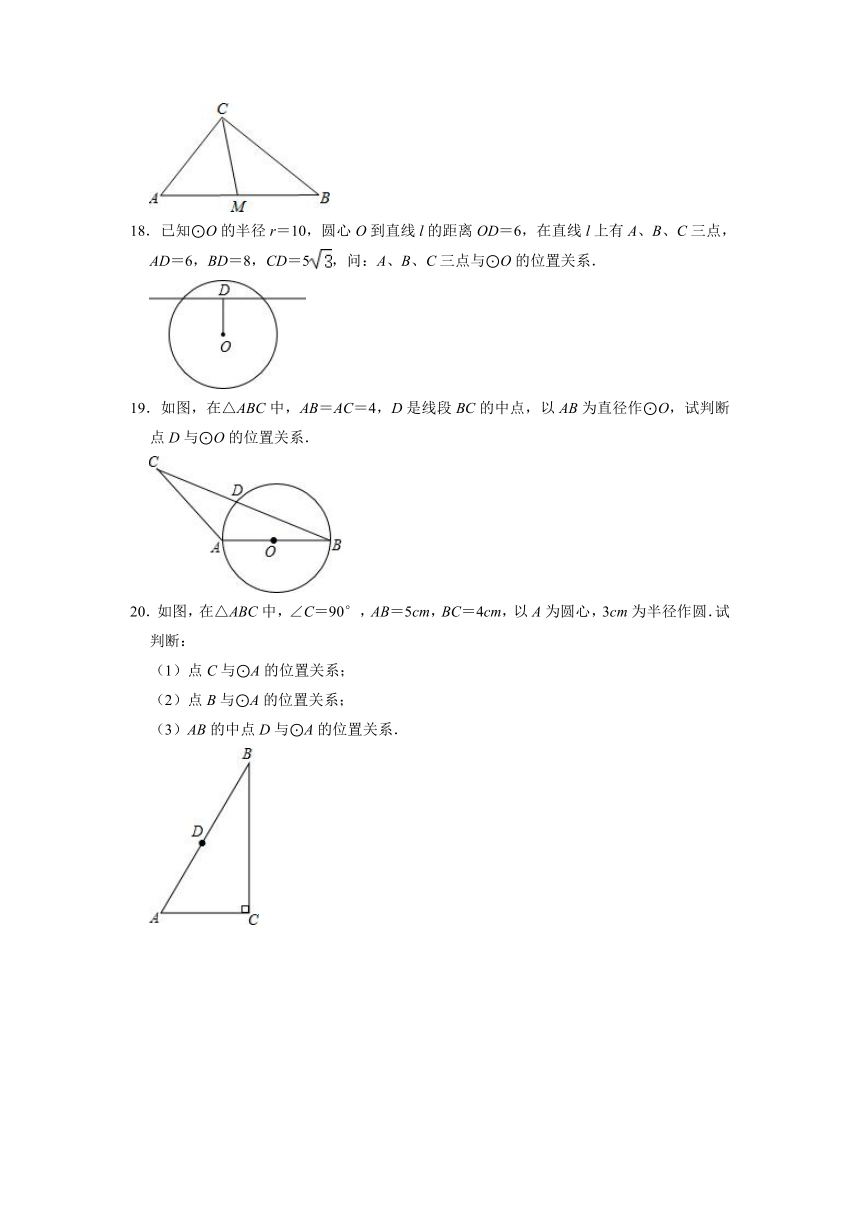
A.点A在⊙O内 B.点A在⊙O上 C.点A在⊙O外 D.不能确定
3.如图,已知矩形中ABCD中,AB=3cm,BC=4cm,若以A为圆心、5cm长为半径画⊙A,则点C与⊙A的位置关系为( )
A.点C在⊙A上 B.点C在⊙A外 C.点C在⊙A内 D.无法判断
4.如图,△ABC为直角三角形,∠C=90°,AC=6,BC=8,以点C为圆心,以CA为半径作⊙C,则△ABC斜边的中点D与⊙C的位置关系是( )
A.点D在⊙C上 B.点D在⊙C内 C.点D在⊙C外 D.不能确定
5.已知⊙O的直径为5,若PO=5,则点P与⊙O的位置关系是( )
A.点P在⊙O内 B.点P在⊙O上 C.点P在⊙O外 D.无法判断
6.⊙O的直径为10厘米,同一平面内,若点P与圆心O的距离为5厘米,则点P与⊙O的位置关系是 .
7.已知⊙O的半径为5cm,点P在⊙O内,则OP 5cm(填“>”、“<”或“=”)
8.已知⊙O的半径为4cm,点A到圆心O的距离为3cm,则点A在⊙O (填“上”“外”或“内”)
9.⊙O的半径为5cm,点A到圆心O的距离OA=3cm,则点A与圆O的位置关系为点A 在圆O .
10.已知一个点到圆上的点的最大距离是5,最小距离是1,则这个圆的直径是 .
11.有一张矩形的纸片,AB=3cm,AD=4cm,若以A为圆心作圆,并且要使点D在⊙A内,而点C在⊙A外,⊙A的半径r的取值范围是 .
12.如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,以BC为直径的半圆交AB于D,P是上的一个动点,连接AP,求AP的最小值.
13.如图,已知△ABC,AC=3,BC=4,∠C=90°,以点C为圆心作⊙C,半径为r.
(1)当r取什么值时,点A、B在⊙C外.
(2)当r在什么范围时,点A在⊙C内,点B在⊙C外.
14.在平面直角坐标系中,有三点A(﹣1,﹣1),P(0,﹣1),Q(﹣2,0),若以点A为圆心、OA长为半径作圆,试判断点P、Q与⊙A的位置关系.
15.如图,在Rt△ABC中,∠C=90°,AC=4,O是BC上一点,且OC=3,E是AO的中点,如以O为圆心,OC为半径作圆,求点E和⊙O的位置关系.
16.如图,已知矩形ABCD的边AB=15,BC=20.若以点A位圆心,以20为半径作⊙A,则点B、C、D与⊙A的位置关系如何?
17.已知如图,在△ABC中,∠C=90°,AC=2,BC=3,AB的中点为点M.
(1)以点C为圆心,2为半径作⊙C,则点A、B、M分别与⊙C有怎样的位置关系?
(2)若以C为圆心作⊙C,使A、B、M三点中至少有一点在⊙C内,且至少有一点在⊙C外,则⊙C的半径r的取值范围是什么?
18.已知⊙O的半径r=10,圆心O到直线l的距离OD=6,在直线l上有A、B、C三点,AD=6,BD=8,CD=5,问:A、B、C三点与⊙O的位置关系.
19.如图,在△ABC中,AB=AC=4,D是线段BC的中点,以AB为直径作⊙O,试判断点D与⊙O的位置关系.
20.如图,在△ABC中,∠C=90°,AB=5cm,BC=4cm,以A为圆心,3cm为半径作圆.试判断:
(1)点C与⊙A的位置关系;
(2)点B与⊙A的位置关系;
(3)AB的中点D与⊙A的位置关系.
参考答案
1.解:∵⊙O的半径为5cm,OA=4cm,
∴点A与⊙O的位置关系是:点A在⊙O内.
故选:A.
2.解:∵圆的半径是4cm,点A到圆心的距离是3cm,小于圆的半径,
∴点A在圆内.
故选:A.
3.解:连接AC,
∵AB=3cm,BC=AD=4cm,
∴AC=5cm,
∴点C在⊙A上,
故选:A.
4.解:∵Rt△ABC中,∠C=Rt∠,AC=6,BC=8,
∴AB==10,
∵D为斜边AB的中点,
CD=AB=5,
d=5,r=6,
∴d<r,
∴点D与⊙C内,
故选:B.
5.解:r==2.5,
∵d=5>2.5,
点P在⊙O外,
故选:C.
6.解:∵d=5=r,
∴点P与⊙O的位置关系是点P的⊙O上,
故答案为点P在⊙O上.
7.解:∵⊙O的半径为5cm,
点P在⊙O内,
∴OP<5cm.
故答案为:<.
8.解:∵OA=3cm<4cm∴点A在⊙O内.
故答案是:内.
9.解:∵⊙O的半径为5cm,点A到圆心O的距离为3cm,
即点A到圆心O的距离小于圆的半径,
∴点A在⊙O内,
故答案为:内.
10.解:分为两种情况:
①当点M在圆内时,如图1,
∵点到圆上的最小距离MB=1,最大距离MA=5,
∴直径AB=1+5=6,
②当点M在圆外时,如图2,
∵点到圆上的最小距离MB=1,最大距离MA=5,
∴直径AB=5﹣1=4,
故答案为:6或4.
11.解:∵矩形的纸片,AB=3cm,AD=4cm,
∴AC=5cm,
∴以A为圆心作圆,并且要使点D在⊙A内,而点C在⊙A外,⊙A的半径r的取值范围为4cm<r<5cm.
故答案为4cm<r<5cm.
12.解:找到BC的中点E,连接AE,交半圆于P2,在半圆上取P1,连接AP1,EP1,
可见,AP1+EP1>AE,
即AP2是AP的最小值,
∵AE==,P2E=1,
∴AP2=﹣1.
13.解:(1)当0<r<3时,点A、B在⊙C外;
(2)当3<r<4时,点A在⊙C内,点B在⊙C外.
14.解:∵A(﹣1,﹣1),P(0,﹣1),Q(﹣2,0),
∴OA==,AP=1,AQ==,
即AP<OA.AQ=OA,
∴点P在⊙A内,点Q在⊙A上.
15.解:在Rt△ACO中,∠C=90°,AC=4,OC=3,
∴OA==5.
又∵E是AO的中点,
∴OE=OA=.
∵OE=<3=OC,
∴点E在⊙O内.
16.解:连接AC.
∵AB=15<20,
∴点B在⊙A内;
∵AD=BC=20,
∴点D在⊙A上;
在△ABC中,∵∠B=90°,AB=15,BC=20,
∴AC=25>20,
∴点C在⊙A外.
17.解:(1)∵在△ABC中,∠C=90°,AC=2,BC=3,AB的中点为点M,
∴AB===,CM=AB=,
∵以点C为圆心,2为半径作⊙C,
∴AC=2,则A在圆上,CM=<2,则M在圆内,BC=2>2,则B在圆外;
(2)以点C为圆心作⊙C,使A、B、M三点中至少有一点在⊙C内时,
r>,
当至少有一点在⊙C外时,
r<3,
故⊙C的半径r的取值范围为:<r<3.
18.解:OA==6,
BO==10,
CO==,
∵⊙O的半径r=10,
∴点A在⊙O内,点B在⊙O上,点C在⊙O外.
19.解:点D在⊙O上.
理由如下:
连接OD,
∵BD=DC,BO=OA,
∴OD是△BAC的中位线,
∴OD=AC,
∵AB=AC=4,
∴OD=AB=2,
∴点D在⊙O上.
20.解:∵∠C=90°,AB=5cm,BC=4cm,
∴AC=3cm,BA=5cm,DA=2.5cm,
(1)∵AC=r=3cm,∴点C在⊙A上;
(2)∵BA=5cm>3cm,∴BA>r,∴点B在⊙A外;
(3)∵DA=2.5cm<3cm,∴DA<r,∴点D在⊙A内.
1.若⊙O的半径为5cm,OA=4cm,则点A与⊙O的位置关系是( )
A.点A在⊙O内 B.点A在⊙O上 C.点A在⊙O外 D.内含
2.已知⊙O的半径为4cm,点A到圆心O的距离为3cm,则点A与⊙O的位置关系是( )
A.点A在⊙O内 B.点A在⊙O上 C.点A在⊙O外 D.不能确定
3.如图,已知矩形中ABCD中,AB=3cm,BC=4cm,若以A为圆心、5cm长为半径画⊙A,则点C与⊙A的位置关系为( )
A.点C在⊙A上 B.点C在⊙A外 C.点C在⊙A内 D.无法判断
4.如图,△ABC为直角三角形,∠C=90°,AC=6,BC=8,以点C为圆心,以CA为半径作⊙C,则△ABC斜边的中点D与⊙C的位置关系是( )
A.点D在⊙C上 B.点D在⊙C内 C.点D在⊙C外 D.不能确定
5.已知⊙O的直径为5,若PO=5,则点P与⊙O的位置关系是( )
A.点P在⊙O内 B.点P在⊙O上 C.点P在⊙O外 D.无法判断
6.⊙O的直径为10厘米,同一平面内,若点P与圆心O的距离为5厘米,则点P与⊙O的位置关系是 .
7.已知⊙O的半径为5cm,点P在⊙O内,则OP 5cm(填“>”、“<”或“=”)
8.已知⊙O的半径为4cm,点A到圆心O的距离为3cm,则点A在⊙O (填“上”“外”或“内”)
9.⊙O的半径为5cm,点A到圆心O的距离OA=3cm,则点A与圆O的位置关系为点A 在圆O .
10.已知一个点到圆上的点的最大距离是5,最小距离是1,则这个圆的直径是 .
11.有一张矩形的纸片,AB=3cm,AD=4cm,若以A为圆心作圆,并且要使点D在⊙A内,而点C在⊙A外,⊙A的半径r的取值范围是 .
12.如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,以BC为直径的半圆交AB于D,P是上的一个动点,连接AP,求AP的最小值.
13.如图,已知△ABC,AC=3,BC=4,∠C=90°,以点C为圆心作⊙C,半径为r.
(1)当r取什么值时,点A、B在⊙C外.
(2)当r在什么范围时,点A在⊙C内,点B在⊙C外.
14.在平面直角坐标系中,有三点A(﹣1,﹣1),P(0,﹣1),Q(﹣2,0),若以点A为圆心、OA长为半径作圆,试判断点P、Q与⊙A的位置关系.
15.如图,在Rt△ABC中,∠C=90°,AC=4,O是BC上一点,且OC=3,E是AO的中点,如以O为圆心,OC为半径作圆,求点E和⊙O的位置关系.
16.如图,已知矩形ABCD的边AB=15,BC=20.若以点A位圆心,以20为半径作⊙A,则点B、C、D与⊙A的位置关系如何?
17.已知如图,在△ABC中,∠C=90°,AC=2,BC=3,AB的中点为点M.
(1)以点C为圆心,2为半径作⊙C,则点A、B、M分别与⊙C有怎样的位置关系?
(2)若以C为圆心作⊙C,使A、B、M三点中至少有一点在⊙C内,且至少有一点在⊙C外,则⊙C的半径r的取值范围是什么?
18.已知⊙O的半径r=10,圆心O到直线l的距离OD=6,在直线l上有A、B、C三点,AD=6,BD=8,CD=5,问:A、B、C三点与⊙O的位置关系.
19.如图,在△ABC中,AB=AC=4,D是线段BC的中点,以AB为直径作⊙O,试判断点D与⊙O的位置关系.
20.如图,在△ABC中,∠C=90°,AB=5cm,BC=4cm,以A为圆心,3cm为半径作圆.试判断:
(1)点C与⊙A的位置关系;
(2)点B与⊙A的位置关系;
(3)AB的中点D与⊙A的位置关系.
参考答案
1.解:∵⊙O的半径为5cm,OA=4cm,
∴点A与⊙O的位置关系是:点A在⊙O内.
故选:A.
2.解:∵圆的半径是4cm,点A到圆心的距离是3cm,小于圆的半径,
∴点A在圆内.
故选:A.
3.解:连接AC,
∵AB=3cm,BC=AD=4cm,
∴AC=5cm,
∴点C在⊙A上,
故选:A.
4.解:∵Rt△ABC中,∠C=Rt∠,AC=6,BC=8,
∴AB==10,
∵D为斜边AB的中点,
CD=AB=5,
d=5,r=6,
∴d<r,
∴点D与⊙C内,
故选:B.
5.解:r==2.5,
∵d=5>2.5,
点P在⊙O外,
故选:C.
6.解:∵d=5=r,
∴点P与⊙O的位置关系是点P的⊙O上,
故答案为点P在⊙O上.
7.解:∵⊙O的半径为5cm,
点P在⊙O内,
∴OP<5cm.
故答案为:<.
8.解:∵OA=3cm<4cm∴点A在⊙O内.
故答案是:内.
9.解:∵⊙O的半径为5cm,点A到圆心O的距离为3cm,
即点A到圆心O的距离小于圆的半径,
∴点A在⊙O内,
故答案为:内.
10.解:分为两种情况:
①当点M在圆内时,如图1,
∵点到圆上的最小距离MB=1,最大距离MA=5,
∴直径AB=1+5=6,
②当点M在圆外时,如图2,
∵点到圆上的最小距离MB=1,最大距离MA=5,
∴直径AB=5﹣1=4,
故答案为:6或4.
11.解:∵矩形的纸片,AB=3cm,AD=4cm,
∴AC=5cm,
∴以A为圆心作圆,并且要使点D在⊙A内,而点C在⊙A外,⊙A的半径r的取值范围为4cm<r<5cm.
故答案为4cm<r<5cm.
12.解:找到BC的中点E,连接AE,交半圆于P2,在半圆上取P1,连接AP1,EP1,
可见,AP1+EP1>AE,
即AP2是AP的最小值,
∵AE==,P2E=1,
∴AP2=﹣1.
13.解:(1)当0<r<3时,点A、B在⊙C外;
(2)当3<r<4时,点A在⊙C内,点B在⊙C外.
14.解:∵A(﹣1,﹣1),P(0,﹣1),Q(﹣2,0),
∴OA==,AP=1,AQ==,
即AP<OA.AQ=OA,
∴点P在⊙A内,点Q在⊙A上.
15.解:在Rt△ACO中,∠C=90°,AC=4,OC=3,
∴OA==5.
又∵E是AO的中点,
∴OE=OA=.
∵OE=<3=OC,
∴点E在⊙O内.
16.解:连接AC.
∵AB=15<20,
∴点B在⊙A内;
∵AD=BC=20,
∴点D在⊙A上;
在△ABC中,∵∠B=90°,AB=15,BC=20,
∴AC=25>20,
∴点C在⊙A外.
17.解:(1)∵在△ABC中,∠C=90°,AC=2,BC=3,AB的中点为点M,
∴AB===,CM=AB=,
∵以点C为圆心,2为半径作⊙C,
∴AC=2,则A在圆上,CM=<2,则M在圆内,BC=2>2,则B在圆外;
(2)以点C为圆心作⊙C,使A、B、M三点中至少有一点在⊙C内时,
r>,
当至少有一点在⊙C外时,
r<3,
故⊙C的半径r的取值范围为:<r<3.
18.解:OA==6,
BO==10,
CO==,
∵⊙O的半径r=10,
∴点A在⊙O内,点B在⊙O上,点C在⊙O外.
19.解:点D在⊙O上.
理由如下:
连接OD,
∵BD=DC,BO=OA,
∴OD是△BAC的中位线,
∴OD=AC,
∵AB=AC=4,
∴OD=AB=2,
∴点D在⊙O上.
20.解:∵∠C=90°,AB=5cm,BC=4cm,
∴AC=3cm,BA=5cm,DA=2.5cm,
(1)∵AC=r=3cm,∴点C在⊙A上;
(2)∵BA=5cm>3cm,∴BA>r,∴点B在⊙A外;
(3)∵DA=2.5cm<3cm,∴DA<r,∴点D在⊙A内.
