北师大版八年级数学上册 1.1 勾股定理的图形验证课件(共15张PPT)
文档属性
| 名称 | 北师大版八年级数学上册 1.1 勾股定理的图形验证课件(共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-27 00:00:00 | ||
图片预览


文档简介
(共15张PPT)
1.1 探索勾股定理(第2课时)
北师大版八年级数学(上)
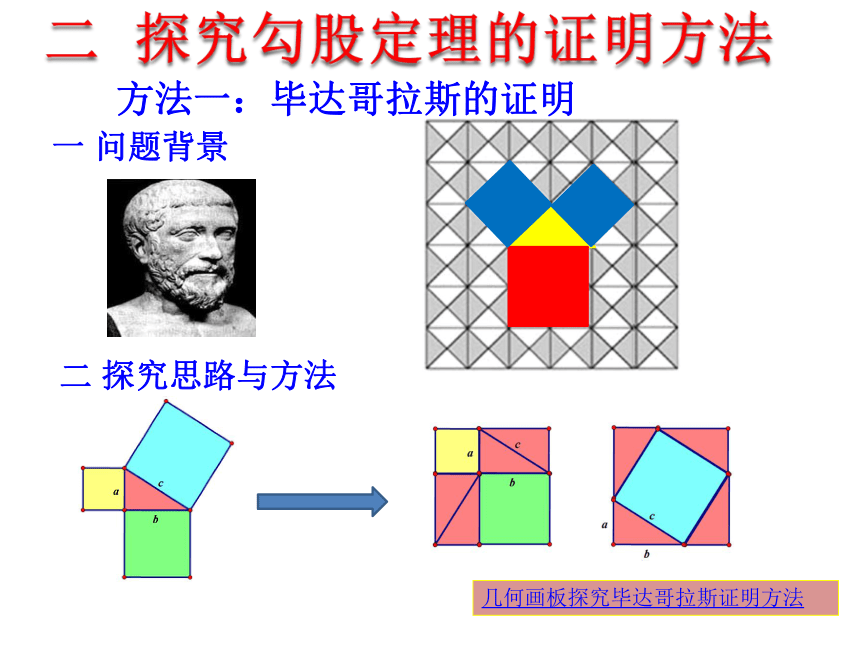
二 探究勾股定理的证明方法
一 问题背景
二 探究思路与方法
几何画板探究毕达哥拉斯证明方法
方法一:毕达哥拉斯的证明
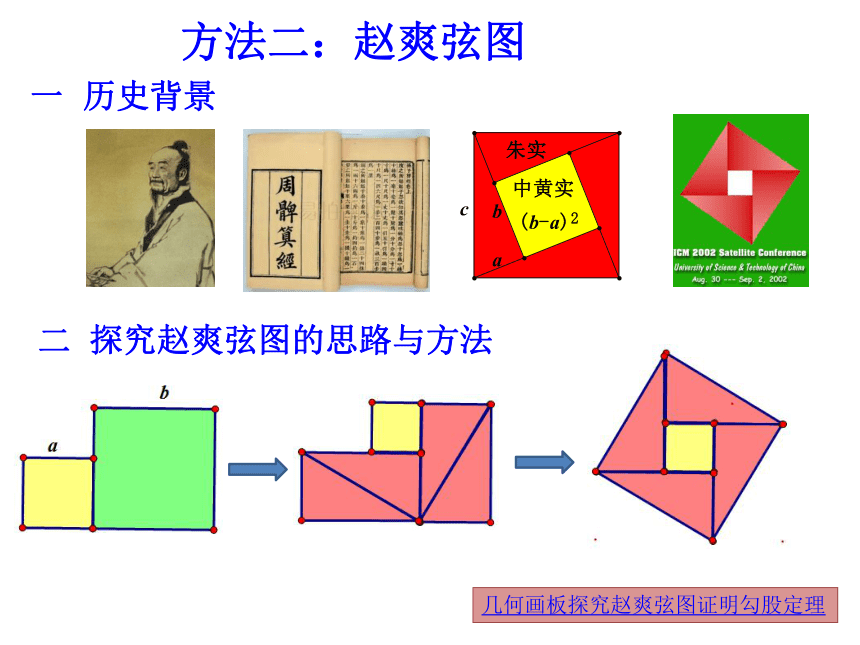
方法二:赵爽弦图
一 历史背景
二 探究赵爽弦图的思路与方法
几何画板探究赵爽弦图证明勾股定理
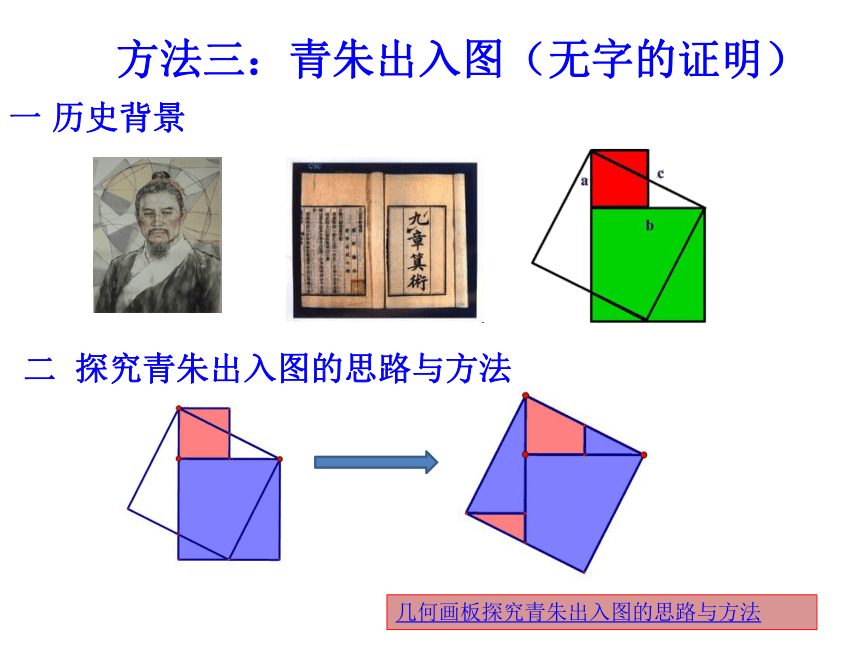
方法三:青朱出入图(无字的证明)
一 历史背景
二 探究青朱出入图的思路与方法
几何画板探究青朱出入图的思路与方法
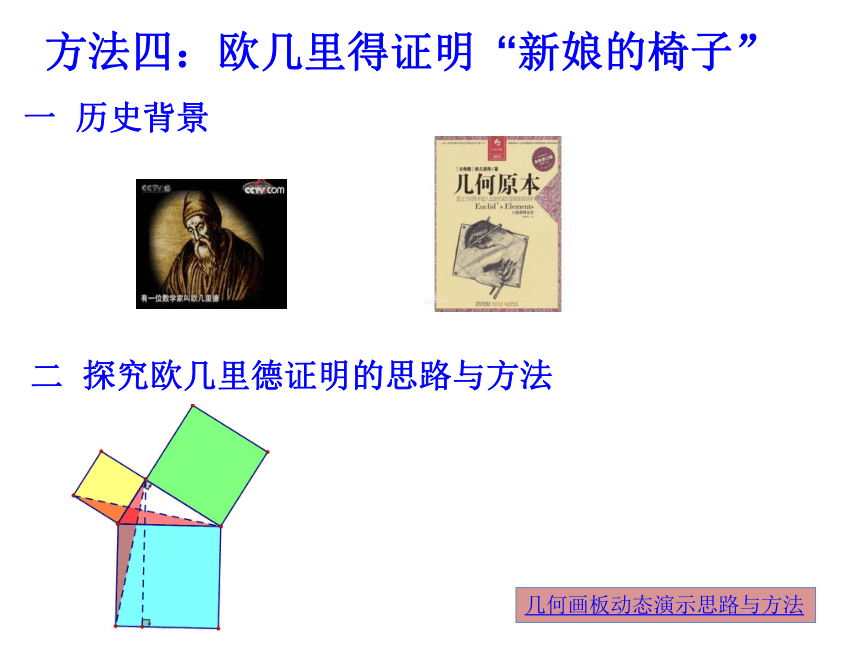
“新娘的椅子”
方法四:欧几里得证明
一 历史背景
二 探究欧几里德证明的思路与方法
几何画板动态演示思路与方法
勾股定理的证明:分三种类型
第一种类型:等面积 两算法
以赵爽的“弦图”为代表,用几何图形的
截、割、拼、补,一图两算来证明代数式之间的恒等关系;
第二种类型:无字证明
以刘徽的“青朱出入图”为代表,“无字证明”。
第三种类型:欧氏几何证明
以欧几里得的证明方法为代表,运用欧氏
几何的基本定理进行证明;
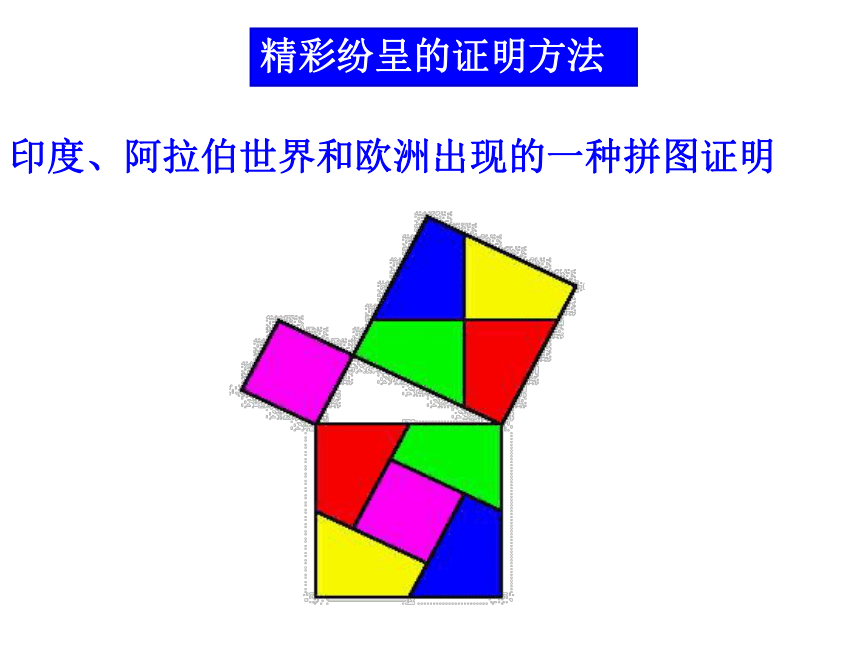
精彩纷呈的证明方法
印度、阿拉伯世界和欧洲出现的一种拼图证明
美国第二十任总统伽菲尔德
总统巧证勾股定理
a
a
b
b
c
c
A
D
C
B
E
达芬奇证法
详细操作步骤:
例:飞机在空中水平飞行,某一时刻刚好飞到一个男孩子头顶上方4 km处,过了20 s,飞机距离这个男孩子头顶5 km,飞机每小时飞行多少千米?
4km
5km
A
B
C
三 勾股定理的应用
解:Rt △ ABC中,由勾股定理得:
AB2 = BC2 + AC2 即 52 = BC2 + 42,
所以 BC=3
飞机20 s飞行了3 km,那么1小时飞行的
距离为: 3 x 3 x 60= 540 km,
即:飞机 每小时飞行540 km。
1.如图1,三个正方形中其中两个面积S2、S3分别为 144、169,则第三个正方形的面积S1为____。
2.如图2,是某沿江地区交通平面图,为了加快经济发展,该地区拟修建一条连接B,C,E三城市的沿江高速,已知沿江高速的建设成本是100万元/ km,该沿江高速的造价预计是多少?
图1
图2
四 课堂练习
解:Rt △ ABC中,由勾股定理得:
BC2 =A B2 + AC2 即BC 2 =30 2 + 402,
所以 BC=50
Rt △ CDE中,由勾股定理得:
CE2 =CD2 + DE2 即CE 2 =50 2 + 1202,
所以 CE=130
所以 BE=BC+CE=180 KM
180 x 100=18000 万元
即:该沿江高速的造价预计是18000 万元
在几何画板演示下,小组讨论:
(1)在前面已经讨论了直角三角形三边满足的关系,那么锐角三角形或钝角三角形的三边是否也满足这一关系呢?
(2)在任意一个三角形中,如果一个角是锐角,那么这个三角形中夹这个锐角两边的平方和与第三边的平方有怎样的大小关系呢 如果这个角是钝角呢 (以下图中的∠ P 为例来探讨)
几何画板动态探究 拓展延伸
五 拓展延伸
六
1.验证勾股定理的三类方法:
第一种类型:等面积 两算法
第二种类型:无字证明
第三种类型:欧氏几何证明
2.勾股定理的初步应用
动态勾股树演示
七 作业
1必做题:
习题1.2: 第1、2 、3题
2选做题:
搜集有关勾股定理的证明方法并选择其中一种方法仔细研究。
1.1 探索勾股定理(第2课时)
北师大版八年级数学(上)
二 探究勾股定理的证明方法
一 问题背景
二 探究思路与方法
几何画板探究毕达哥拉斯证明方法
方法一:毕达哥拉斯的证明
方法二:赵爽弦图
一 历史背景
二 探究赵爽弦图的思路与方法
几何画板探究赵爽弦图证明勾股定理
方法三:青朱出入图(无字的证明)
一 历史背景
二 探究青朱出入图的思路与方法
几何画板探究青朱出入图的思路与方法
“新娘的椅子”
方法四:欧几里得证明
一 历史背景
二 探究欧几里德证明的思路与方法
几何画板动态演示思路与方法
勾股定理的证明:分三种类型
第一种类型:等面积 两算法
以赵爽的“弦图”为代表,用几何图形的
截、割、拼、补,一图两算来证明代数式之间的恒等关系;
第二种类型:无字证明
以刘徽的“青朱出入图”为代表,“无字证明”。
第三种类型:欧氏几何证明
以欧几里得的证明方法为代表,运用欧氏
几何的基本定理进行证明;
精彩纷呈的证明方法
印度、阿拉伯世界和欧洲出现的一种拼图证明
美国第二十任总统伽菲尔德
总统巧证勾股定理
a
a
b
b
c
c
A
D
C
B
E
达芬奇证法
详细操作步骤:
例:飞机在空中水平飞行,某一时刻刚好飞到一个男孩子头顶上方4 km处,过了20 s,飞机距离这个男孩子头顶5 km,飞机每小时飞行多少千米?
4km
5km
A
B
C
三 勾股定理的应用
解:Rt △ ABC中,由勾股定理得:
AB2 = BC2 + AC2 即 52 = BC2 + 42,
所以 BC=3
飞机20 s飞行了3 km,那么1小时飞行的
距离为: 3 x 3 x 60= 540 km,
即:飞机 每小时飞行540 km。
1.如图1,三个正方形中其中两个面积S2、S3分别为 144、169,则第三个正方形的面积S1为____。
2.如图2,是某沿江地区交通平面图,为了加快经济发展,该地区拟修建一条连接B,C,E三城市的沿江高速,已知沿江高速的建设成本是100万元/ km,该沿江高速的造价预计是多少?
图1
图2
四 课堂练习
解:Rt △ ABC中,由勾股定理得:
BC2 =A B2 + AC2 即BC 2 =30 2 + 402,
所以 BC=50
Rt △ CDE中,由勾股定理得:
CE2 =CD2 + DE2 即CE 2 =50 2 + 1202,
所以 CE=130
所以 BE=BC+CE=180 KM
180 x 100=18000 万元
即:该沿江高速的造价预计是18000 万元
在几何画板演示下,小组讨论:
(1)在前面已经讨论了直角三角形三边满足的关系,那么锐角三角形或钝角三角形的三边是否也满足这一关系呢?
(2)在任意一个三角形中,如果一个角是锐角,那么这个三角形中夹这个锐角两边的平方和与第三边的平方有怎样的大小关系呢 如果这个角是钝角呢 (以下图中的∠ P 为例来探讨)
几何画板动态探究 拓展延伸
五 拓展延伸
六
1.验证勾股定理的三类方法:
第一种类型:等面积 两算法
第二种类型:无字证明
第三种类型:欧氏几何证明
2.勾股定理的初步应用
动态勾股树演示
七 作业
1必做题:
习题1.2: 第1、2 、3题
2选做题:
搜集有关勾股定理的证明方法并选择其中一种方法仔细研究。
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
