函数的单调性

(共17张PPT)
能用图象上动点P（x，y）的横、纵坐标的大小变化来说明图象的上升或下降吗？
x
y
o
在y轴的右侧,随着x的增大,f(x)的值随着增大.
在y轴的左侧,随着x的增大,f(x)的值随着减小。
局部上升或下降
那么就说在f(x)在区间D上是
减函数，称D为f(x)的 减 区间.
O
x
y
x1
x2
f(x1)
f(x2)
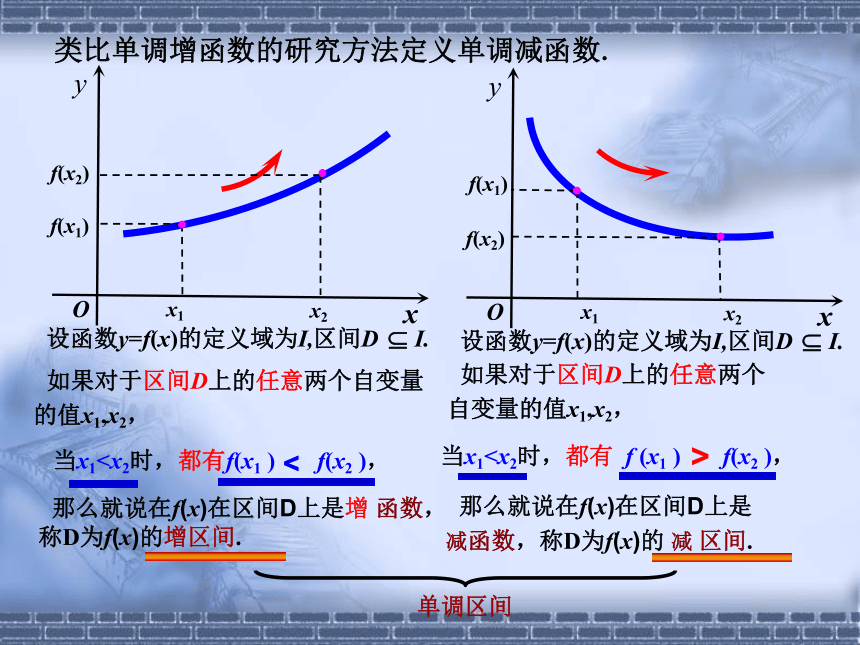
类比单调增函数的研究方法定义单调减函数.
x
O
y
x1
x2
f(x1)
f(x2)
设函数y=f(x)的定义域为I,区间D I.
如果对于区间D上的任意两个自变量
的值x1,x2，
设函数y=f(x)的定义域为I,区间D I.
如果对于区间D上的任意两个
自变量的值x1,x2，
那么就说在f(x)在区间D上是增 函数，称D为f(x)的增区间.
当x1<
当x1<
>
单调区间
（2）函数单调性是针对某个区间而言的，是一个局部性质;
定义:如果函数 y =f(x)在区间D上是增函数或减函数，那么就说函数 y =f(x)在这一区间具有单调性。
图象特征:增函数的图象是上升的，减函数的图象是下降的。
判断1：函数 f (x)= x2 在 是单调增函数吗
x
y
o
（1） x 1, x 2 取值的任意性
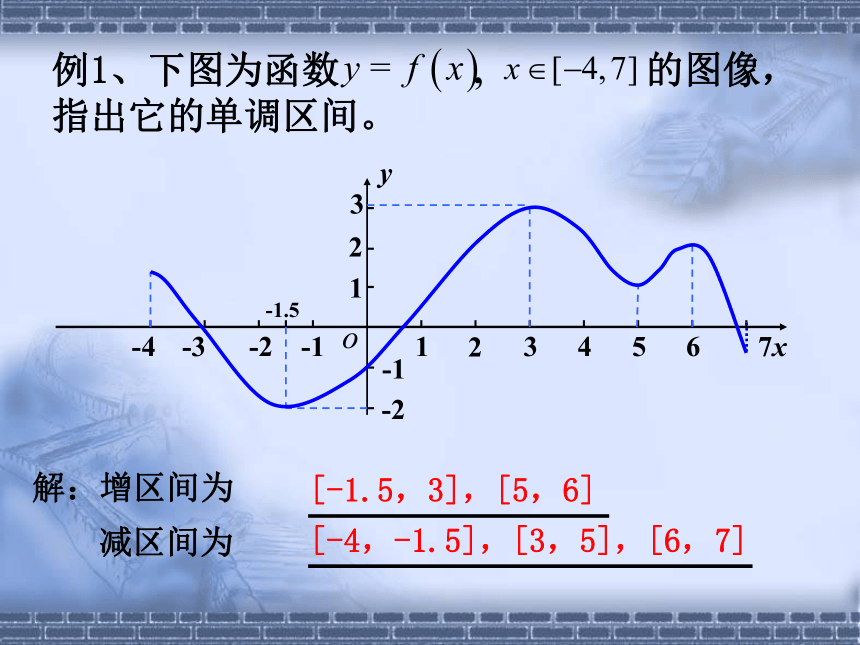
例1、下图为函数 , 的图像，指出它的单调区间。
1
2
3
-2
-3
-2
-1
1
2
3
4
5
6
7
x
o
-4
-1
y
-1.5
[-1.5，3]，[5，6]
[-4，-1.5]，[3，5]，[6，7]
解：增区间为
减区间为
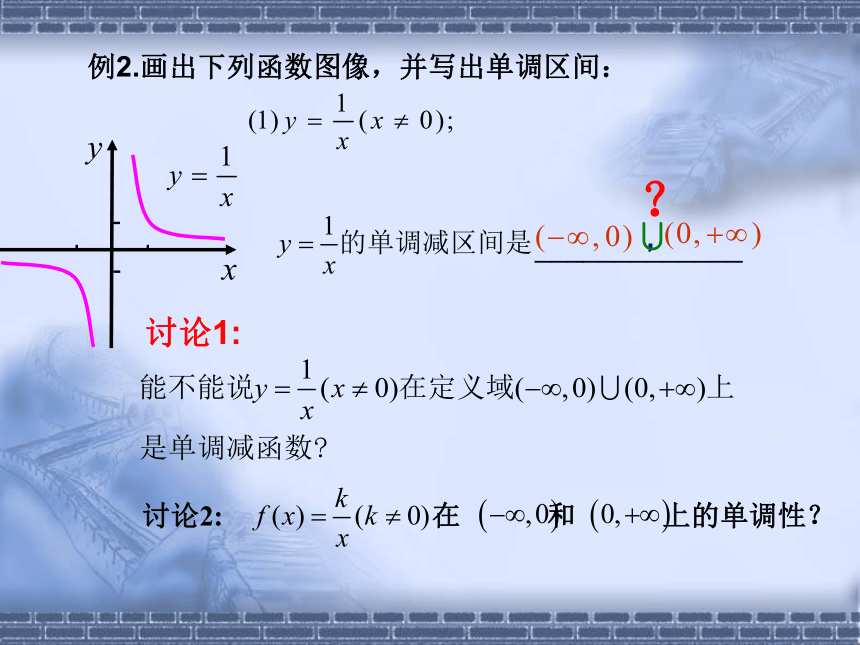
例2.画出下列函数图像，并写出单调区间：
x
y
_____________
,
讨论1:
讨论2: 　　　　　　　在　　　和　　　上的单调性？
？
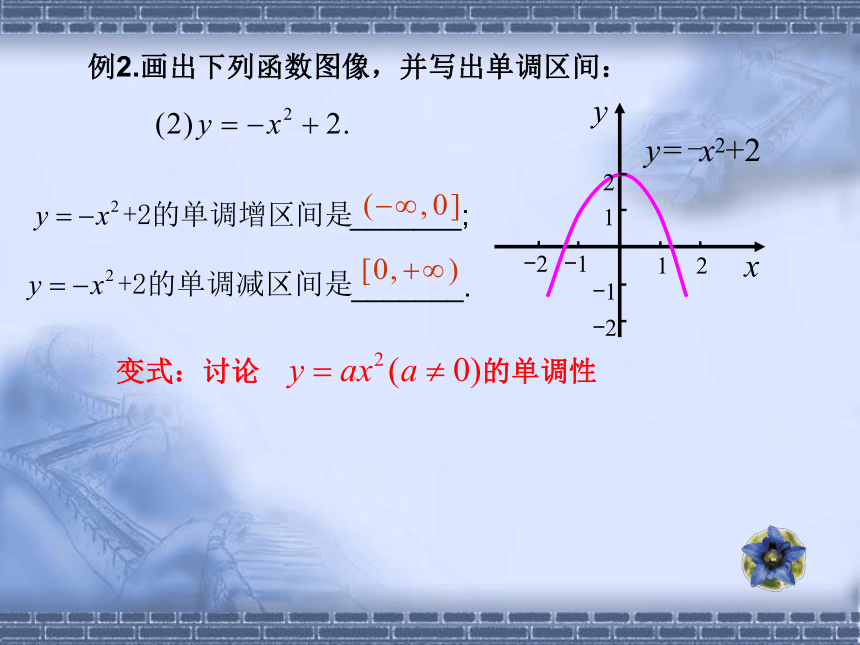
变式：讨论 的单调性
x
y
y=-x2+2
1
-1
1
2
2
-1
-2
-2
_______;
_______.
例2.画出下列函数图像，并写出单调区间：
1. 取值(任取x1，x2∈D，且x12. 作差f(x1)－f(x2)；
3. 变形（通常是因式分解和配方,要注意变形到能判断差的符号为止）；
4. 定号（即判断差f(x1)－f(x2)的正负,要注意说清理由）；
5. 下结论
一般步骤:
用定义法证明函数 　
在区间 上是增函数。
课堂小结
1.增函数与减函数的定义中有哪些关键点？
2.有定义证明函数的单调性的一般步骤是什么？
3. 判断函数的单调性有哪些常用方法？
补充作业:
1、证明函数 f（x）=-x2-2x+3在 上是 减函数。
2、证明函数 f（x）= 在 上是增函数。
数与形,本是相倚依,
焉能分作两边飞;
数无形时少直觉,
形少数时难入微;
数形结合百般好,
隔离分家万事休;
切莫忘,几何代数统一体,
永远联系莫分离.
——华罗庚
证明：在区间 上任取两个值 且
则
，且
所以函数 在区间上 是增函数.
取值
作差
变形
定号
结论
返回
返回
是定义在R上的单调函数，且 的图
象过点A（0，2）和B（3，0）
（1）解方程
（2）解不等式
（3）求适合 的 的取值范围
成果运用
若二次函数 的单调增区间是 ， 则a的取值情况是 （ ）
变式1
若二次函数 在区间 上单调递增，求a的取值范围。
A. B. C. D.
________
成果运用
若二次函数 在区间 上单调递增，求a的取值范围。
解：二次函数 的对称轴为 ,
由图象可知只要 ，即 即可.
o
x
y
1
x
y
1
o