山东省济南市长清区第一高级中学2021-2022学年高一上学期期中考试数学试卷(PDF版含答案)
文档属性
| 名称 | 山东省济南市长清区第一高级中学2021-2022学年高一上学期期中考试数学试卷(PDF版含答案) |

|
|
| 格式 | |||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-26 00:00:00 | ||
图片预览



文档简介
2021-2022 学年度上学期高一年级期中考试
数学试题
注意事项:
1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码
粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用 2B 铅笔把答题卡上对应题目的答案标号涂黑,
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。写在试题卷、草稿
纸和答题卡上的非答题区域均无效。
第Ⅰ卷
一、单项选择题:本题共 8 小题,每小题 5 分,共 40 分.在每小题给出的四个选
项中,只有一项是符合题目要求的.
1.已知集合 A={-1,0,m}, B={1,2},若 AUB={-1,0,1,2},则实数m的值为( )
A.-1或 0 B.0 或1 C.-1或2 D.1或2
2.命题“ x R, | x | x 1 0”的否定是( )
A. x R, | x | x 1 0 B. x R , | x | x 1 0
C. x R, | x | x 1 0 D. x R, | x | x 1 0
3.下列各组函数中,表示同一函数的是( )
A. f (x) x, g(x) x2 B. f (x) x, g(x) ( x )2
2 x 1(x 1)
C. f (x) x, g(x) x D. f (x) | x 1|, g(x)
x 1 x(x 1)
4.已知实数0 a 1,则下列正确的是( )
1 1 1 1
A. a a2 B. a a2 C. a2 a D. a2 a
a a a a
x 4
5.若函数 f (x) 2 的定义域为R ,则实数m的取值范围是( )mx 4mx 3
1
(0, 3] [0, 3] 3 3A. B. C.[0, ) D. (0, )
4 4 4 4
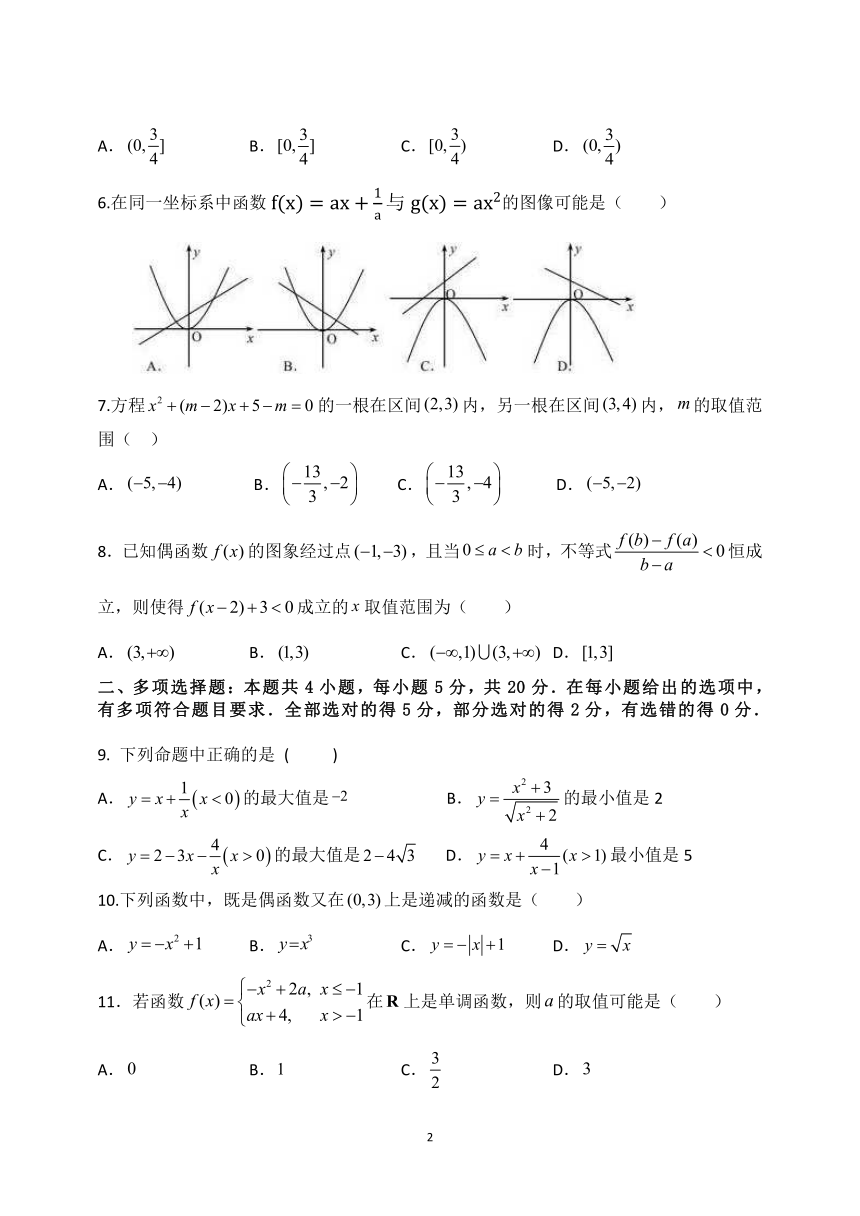
6. 1在同一坐标系中函数 f(x) = ax + 与 g(x) = ax2的图像可能是( )
a
7.方程 x2 (m 2)x 5 m 0的一根在区间 (2,3)内,另一根在区间 (3, 4)内,m的取值范
围( )
A. ( 5, 4)
13 , 2 13 B. 3
C. , 4 D. ( 5, 2)
3
8.已知偶函数 f (x) f (b) f (a)的图象经过点 ( 1, 3),且当0 a b时,不等式 0恒成
b a
立,则使得 f (x 2) 3 0成立的 x取值范围为( )
A. (3, ) B. (1,3) C. ( ,1) (3, ) D.[1,3]
二、多项选择题:本题共 4 小题,每小题 5 分,共 20 分.在每小题给出的选项中,
有多项符合题目要求.全部选对的得 5 分,部分选对的得 2 分,有选错的得 0 分.
9. 下列命题中正确的是 ( )
A y x 1 x
2 3
. x 0 的最大值是 2 B. y 的最小值是 2
x x2 2
C. y 2 3x 4 4 x 0 的最大值是 2 4 3 D. y x (x 1)最小值是 5
x x 1
10.下列函数中,既是偶函数又在 (0,3)上是递减的函数是( )
A y x2. 1 B. y x3 C. y x 1 D. y x
x2 2a, x 1
11.若函数 f (x) 在R 上是单调函数,则a的取值可能是( )
ax 4, x 1
3
A.0 B.1 C. D.3
2
2
12.我们把定义域为[0, +∞)且同时满足以下两个条件的函数 f(x)称为“Ω函数”:
(1)对任意的 x∈ [0, + ∞),总有 f(x)≥0;
(2)若 x ≥ 0, y ≥ 0,则有 f(x + y) ≥ f(x) + f(y)成立,下列判断正确的是( )
A.若 f(x)为“Ω函数”,则 f(0)=0
B.若 f(x)为“Ω函数”,则 f(x)在[0, +∞)上为增函数
g(x) = 0, x ∈ Q,C.函数 1, x Q在[0, +∞)上是“Ω函数”
D.函数 g(x) = x2 + x在[0, + ∞)上是“Ω函数”
第Ⅱ卷
三、填空题:本大题共 4 小题,每小题 5 分.
13.设集合P x y x2 4x 3 ,Q {x x2 4},则 P ∩ Q = .
14.已知 f (x 1)的定义域为[ 2,3),则 f (x 2)的定义域是 .
15. p : x R , x2 x a 0 .若 p 是真命题,则实数 a 的取值范围是 .
f (x), f (x) g(x)
16.已知函数 f (x)
1 x 2 2x 3 g(x) | 3 , x 3 |,若函数 F (x)
4 2 g(x), f (x) g(x)
,
则 F (2) , F (x)的最大值为 .
四、解答题:本大题共 6 个大题,共 70 分,解答应写出文字说明、证明过程或演
算步骤.
17.(10分)已知集合 A {x∣2a 3 x 3a 1},集合 B {x∣ 5 x 4} .
(1)若 A B,求实数 a的取值范围;
(2)是否存在实数 a,使得 A B?若存在,求出 a的值;若不存在,请说明理由.
18.(12 分)已知二次函数 f (x) x2 4x 3,非空集合 A {x | 0 x a}.
(1)当 x A时,二次函数的最小值为 1,求实数a的取值范围;
(2)当 时,求二次函数 f (x) x2 4x 3的最值以及取到最值时 x的取值.
在①a 1,②a 4,③a 5,这三个条件中任选一个补充在(2)问中的横线上,并求
解. (注:如果选择多个条件分别解答,按第一个解答计分.)
3
19.(12分)已知函数 f (2x) 2 x,g(x)是二次函数,且满足 g(0) 1,g(x 1) g(x) 2x .
(1)求 f (x), g(x)的解析式;
f (x) , x < 0,
(2)设 F (x) g(x) x 0.,求不等式 F(x) ≤ 3的解集. , ≥
20.(12分)已知关于 x的不等式 ax2 3x + 2 > 0的解集为{x|x < 1或 x > b}.
(1)求 a,b的值;
a b
(2)当 x > 0,y > 0且 + = 1 时,有 2x + y ≥ k2 + k + 2恒成立,求 k的取值范围.x y
21.(12分)已知函数 f (x) | x | 1
x 2
.
1
(1)证明: f (x)为偶函数;
(2)用定义证明: f (x)是 (1, )上的减函数;
(3)当 x [ 4, 2]时,求 f (x)的值域.
22.(12分)某企业开发了一种大型电子产品,生产这种产品的年固定成本为 2500万元,
每生产 x百件,需另投入成本 c x( 单位:万元),当年产量不足 30百件时,c x 10x 2 100x;
10000
当年产量不小于 30百件时,c x 501x 4500 .x 若每件电子产品的售价为 5 万元,通
过市场分析,该企业生产的电子产品能全部销售完.
(1)求年利润 y(万元)关于年产量 x(百件)的函数关系式;
(2)年产量为多少百件时,该企业在这一电子产品的生产中获利最大?
4
2021-2022 学年度上学期高一年级期中考试
数 学 答 案
一.单选题 DBDA CACC
二.多选题 ACD AC BC ABD
1
三.填空题 13.[1,2) 14.[1,6) 15.[ ,+∞) 16.0,6
4
17.【解析】(1)当 A 时, 2a 3 3a 1,解得 a 4 ..........................2 分
2a 3 5,
当 A 时, 3a 1 4, 解得 1 a 1........................................................5 分
2a 3 3a 1,
综上,实数 a的取值范围是{a∣a 4 或 1 a 1} ..........................................6 分
(2)不存在.理由如下:若存在实数 a,使 A B,则必有
2a 3 5, a 1,
3a 1 4, 解得 a 1, 无解,........................................................ ...........9 分
故不存在实数 a,使得 A B ............................................................................10 分
18.【解析】(1)作出二次函数 f (x) x2 4x 3 (x 2)2 1的图象如图所示,
当0 x a,二次函数的最小值为 1 ,则a的取值范围为 a 2 ..........6 分
(2)选择方案①,
由图像可知,当a 1 时, f (x)max f (0) 3 ,此时 x 0,
f (x)min f (1) 0 ,此时 x 1.................................................................12 分
选择方案②,
当a 4时, f (x)max f (0) f (4) 3,此时 x 0或 x 4,
f (x)min f (2) 1,此时 x 2 ...................................................................12 分
选择方案③,
当a 5时, f (x)max f (5) 8,此时 x 5,
f (x)min f (2) 1,此时 x 2...................................................................12 分
19【解析】(1)设 2x t t, x ,所以 f (t) 2 t
2 2
即 f (x) 2
x
, ------------2 分
2
因为 g(x) 2是二次函数,所以设 g(x) ax bx c,
因为 g(0) 1,所以 c 1, -------------3 分
g(x 1) g(x) a(x 1)2 b(x 1) 1 [ax2 bx 1]
2ax a2 b, -------------4 分
所以 2ax a + b 2x, 2a 2且a b 0,
解得 a 1,b 1,
所以 g(x) x2 x 1; -------------6 分
2 x , x 0,
(2)由(1)可知 F (x) 2 -------------7 分
x
2 x 1, x 0.
x 0,
x 0,
F (x) 3等价于 x ,或 2 , -------------9 分
2 3. 2
x x 1 3
x 0, x 0,
解得 ,或 , -------------11 分
x 2 1 x 2
所以 2 x 0 或0 x 2,
所以 2 x 2 . -------------12 分
20.【解析】(1)因为不等式 ax2 3x + 2 > 0的解集为{x|x < 1或 x > b},
所以 1和 b是方程 ax2 3x + 2 = 0的两个实数根且 a > 0,
1 + b = 3
a a = 1所以 2 ,解得 b = 2,...........................................................................4 分1·b =
a
(2) (1) a = 1 1 2由 知 b = 2,于是有 + = 1,x y
故 2x + y = (2x + y)( 1 + 2 ) = 4 + y+ 4x ≥ 8,
x y x y
x = 2
当且仅当 y = 4时,等号成立,.....................................................................8 分
依题意有(2x + y)min ≥ k2 + k + 2,即 8 ≥ k2 + k + 2,
得k2 + k 6 ≤ 0 3 ≤ k ≤ 2,
所以 k的取值范围为[ 3,2]........................................................................12 分
21.【解析】(1)函数 f (x) 的定义域是{x | x R ,且 x 1},任取 x {x | x R ,且
x 1},............................................................................................................2 分
都有 f ( x)
| x | 1 | x | 1
( x)2
2 f (x), 1 x 1
f (x)是偶函数.................................................................................................4 分
(2 | x | 1 x 1 1)当 x 1时, f (x) 2 ,任取 x1, x2 (1, )2 ,且 x1 x ,x 1 x 1 x 1 2
则 f x1 f x2
1 1
x1 1 x2 1
x
2
x1
,x1 1 x2 1
1 x1 x2 , x1 1 0, x2 1 0 , x2 x1 0 ,
f x1 f x2 0,即 f x1 f x2 ,
f (x)在 (1, )上是减函数.............................................................................9 分
(3)由(1)(2)知函数 f (x) 在[ 4, 2] 上是增函数,
f (x) f ( 4) | 4 | 1 1 | 2 | 1 min 2 f (x)( 4) 1 3 , max
f ( 2) 1
( 2)2 1 ,
1
所求值域为 ,1 .........................................................................................12 分 3
22.【解析】(1)当 0 x 30 时,
y 500x 10x2 100x 2500 10x2 400x 2500 ;
x 30 10000当 时,y 500x 501x 4500 2500 2000
x 10000
x . x
10x2 400x 2500,0 x 30,
y 2000 x 10000 , x 30. ............................................................5 分
x
(2)当 0 x 30时, y 10(x 20)2 1500,
当 x 20 时, ymax 1500 ;.............................................................................8
分
当 x 30 y 2000 10000 时, x 2000 2 x
10000
2000 200 1800 ,
x x
当且仅当 x
10000
x ,即
x 100时取等号,....................................................11 分
1800 1500 ,
年产量为 100百件时,该企业获得利润最大,最大利润为 1800 万元.....12 分
数学试题
注意事项:
1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码
粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用 2B 铅笔把答题卡上对应题目的答案标号涂黑,
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。写在试题卷、草稿
纸和答题卡上的非答题区域均无效。
第Ⅰ卷
一、单项选择题:本题共 8 小题,每小题 5 分,共 40 分.在每小题给出的四个选
项中,只有一项是符合题目要求的.
1.已知集合 A={-1,0,m}, B={1,2},若 AUB={-1,0,1,2},则实数m的值为( )
A.-1或 0 B.0 或1 C.-1或2 D.1或2
2.命题“ x R, | x | x 1 0”的否定是( )
A. x R, | x | x 1 0 B. x R , | x | x 1 0
C. x R, | x | x 1 0 D. x R, | x | x 1 0
3.下列各组函数中,表示同一函数的是( )
A. f (x) x, g(x) x2 B. f (x) x, g(x) ( x )2
2 x 1(x 1)
C. f (x) x, g(x) x D. f (x) | x 1|, g(x)
x 1 x(x 1)
4.已知实数0 a 1,则下列正确的是( )
1 1 1 1
A. a a2 B. a a2 C. a2 a D. a2 a
a a a a
x 4
5.若函数 f (x) 2 的定义域为R ,则实数m的取值范围是( )mx 4mx 3
1
(0, 3] [0, 3] 3 3A. B. C.[0, ) D. (0, )
4 4 4 4
6. 1在同一坐标系中函数 f(x) = ax + 与 g(x) = ax2的图像可能是( )
a
7.方程 x2 (m 2)x 5 m 0的一根在区间 (2,3)内,另一根在区间 (3, 4)内,m的取值范
围( )
A. ( 5, 4)
13 , 2 13 B. 3
C. , 4 D. ( 5, 2)
3
8.已知偶函数 f (x) f (b) f (a)的图象经过点 ( 1, 3),且当0 a b时,不等式 0恒成
b a
立,则使得 f (x 2) 3 0成立的 x取值范围为( )
A. (3, ) B. (1,3) C. ( ,1) (3, ) D.[1,3]
二、多项选择题:本题共 4 小题,每小题 5 分,共 20 分.在每小题给出的选项中,
有多项符合题目要求.全部选对的得 5 分,部分选对的得 2 分,有选错的得 0 分.
9. 下列命题中正确的是 ( )
A y x 1 x
2 3
. x 0 的最大值是 2 B. y 的最小值是 2
x x2 2
C. y 2 3x 4 4 x 0 的最大值是 2 4 3 D. y x (x 1)最小值是 5
x x 1
10.下列函数中,既是偶函数又在 (0,3)上是递减的函数是( )
A y x2. 1 B. y x3 C. y x 1 D. y x
x2 2a, x 1
11.若函数 f (x) 在R 上是单调函数,则a的取值可能是( )
ax 4, x 1
3
A.0 B.1 C. D.3
2
2
12.我们把定义域为[0, +∞)且同时满足以下两个条件的函数 f(x)称为“Ω函数”:
(1)对任意的 x∈ [0, + ∞),总有 f(x)≥0;
(2)若 x ≥ 0, y ≥ 0,则有 f(x + y) ≥ f(x) + f(y)成立,下列判断正确的是( )
A.若 f(x)为“Ω函数”,则 f(0)=0
B.若 f(x)为“Ω函数”,则 f(x)在[0, +∞)上为增函数
g(x) = 0, x ∈ Q,C.函数 1, x Q在[0, +∞)上是“Ω函数”
D.函数 g(x) = x2 + x在[0, + ∞)上是“Ω函数”
第Ⅱ卷
三、填空题:本大题共 4 小题,每小题 5 分.
13.设集合P x y x2 4x 3 ,Q {x x2 4},则 P ∩ Q = .
14.已知 f (x 1)的定义域为[ 2,3),则 f (x 2)的定义域是 .
15. p : x R , x2 x a 0 .若 p 是真命题,则实数 a 的取值范围是 .
f (x), f (x) g(x)
16.已知函数 f (x)
1 x 2 2x 3 g(x) | 3 , x 3 |,若函数 F (x)
4 2 g(x), f (x) g(x)
,
则 F (2) , F (x)的最大值为 .
四、解答题:本大题共 6 个大题,共 70 分,解答应写出文字说明、证明过程或演
算步骤.
17.(10分)已知集合 A {x∣2a 3 x 3a 1},集合 B {x∣ 5 x 4} .
(1)若 A B,求实数 a的取值范围;
(2)是否存在实数 a,使得 A B?若存在,求出 a的值;若不存在,请说明理由.
18.(12 分)已知二次函数 f (x) x2 4x 3,非空集合 A {x | 0 x a}.
(1)当 x A时,二次函数的最小值为 1,求实数a的取值范围;
(2)当 时,求二次函数 f (x) x2 4x 3的最值以及取到最值时 x的取值.
在①a 1,②a 4,③a 5,这三个条件中任选一个补充在(2)问中的横线上,并求
解. (注:如果选择多个条件分别解答,按第一个解答计分.)
3
19.(12分)已知函数 f (2x) 2 x,g(x)是二次函数,且满足 g(0) 1,g(x 1) g(x) 2x .
(1)求 f (x), g(x)的解析式;
f (x) , x < 0,
(2)设 F (x) g(x) x 0.,求不等式 F(x) ≤ 3的解集. , ≥
20.(12分)已知关于 x的不等式 ax2 3x + 2 > 0的解集为{x|x < 1或 x > b}.
(1)求 a,b的值;
a b
(2)当 x > 0,y > 0且 + = 1 时,有 2x + y ≥ k2 + k + 2恒成立,求 k的取值范围.x y
21.(12分)已知函数 f (x) | x | 1
x 2
.
1
(1)证明: f (x)为偶函数;
(2)用定义证明: f (x)是 (1, )上的减函数;
(3)当 x [ 4, 2]时,求 f (x)的值域.
22.(12分)某企业开发了一种大型电子产品,生产这种产品的年固定成本为 2500万元,
每生产 x百件,需另投入成本 c x( 单位:万元),当年产量不足 30百件时,c x 10x 2 100x;
10000
当年产量不小于 30百件时,c x 501x 4500 .x 若每件电子产品的售价为 5 万元,通
过市场分析,该企业生产的电子产品能全部销售完.
(1)求年利润 y(万元)关于年产量 x(百件)的函数关系式;
(2)年产量为多少百件时,该企业在这一电子产品的生产中获利最大?
4
2021-2022 学年度上学期高一年级期中考试
数 学 答 案
一.单选题 DBDA CACC
二.多选题 ACD AC BC ABD
1
三.填空题 13.[1,2) 14.[1,6) 15.[ ,+∞) 16.0,6
4
17.【解析】(1)当 A 时, 2a 3 3a 1,解得 a 4 ..........................2 分
2a 3 5,
当 A 时, 3a 1 4, 解得 1 a 1........................................................5 分
2a 3 3a 1,
综上,实数 a的取值范围是{a∣a 4 或 1 a 1} ..........................................6 分
(2)不存在.理由如下:若存在实数 a,使 A B,则必有
2a 3 5, a 1,
3a 1 4, 解得 a 1, 无解,........................................................ ...........9 分
故不存在实数 a,使得 A B ............................................................................10 分
18.【解析】(1)作出二次函数 f (x) x2 4x 3 (x 2)2 1的图象如图所示,
当0 x a,二次函数的最小值为 1 ,则a的取值范围为 a 2 ..........6 分
(2)选择方案①,
由图像可知,当a 1 时, f (x)max f (0) 3 ,此时 x 0,
f (x)min f (1) 0 ,此时 x 1.................................................................12 分
选择方案②,
当a 4时, f (x)max f (0) f (4) 3,此时 x 0或 x 4,
f (x)min f (2) 1,此时 x 2 ...................................................................12 分
选择方案③,
当a 5时, f (x)max f (5) 8,此时 x 5,
f (x)min f (2) 1,此时 x 2...................................................................12 分
19【解析】(1)设 2x t t, x ,所以 f (t) 2 t
2 2
即 f (x) 2
x
, ------------2 分
2
因为 g(x) 2是二次函数,所以设 g(x) ax bx c,
因为 g(0) 1,所以 c 1, -------------3 分
g(x 1) g(x) a(x 1)2 b(x 1) 1 [ax2 bx 1]
2ax a2 b, -------------4 分
所以 2ax a + b 2x, 2a 2且a b 0,
解得 a 1,b 1,
所以 g(x) x2 x 1; -------------6 分
2 x , x 0,
(2)由(1)可知 F (x) 2 -------------7 分
x
2 x 1, x 0.
x 0,
x 0,
F (x) 3等价于 x ,或 2 , -------------9 分
2 3. 2
x x 1 3
x 0, x 0,
解得 ,或 , -------------11 分
x 2 1 x 2
所以 2 x 0 或0 x 2,
所以 2 x 2 . -------------12 分
20.【解析】(1)因为不等式 ax2 3x + 2 > 0的解集为{x|x < 1或 x > b},
所以 1和 b是方程 ax2 3x + 2 = 0的两个实数根且 a > 0,
1 + b = 3
a a = 1所以 2 ,解得 b = 2,...........................................................................4 分1·b =
a
(2) (1) a = 1 1 2由 知 b = 2,于是有 + = 1,x y
故 2x + y = (2x + y)( 1 + 2 ) = 4 + y+ 4x ≥ 8,
x y x y
x = 2
当且仅当 y = 4时,等号成立,.....................................................................8 分
依题意有(2x + y)min ≥ k2 + k + 2,即 8 ≥ k2 + k + 2,
得k2 + k 6 ≤ 0 3 ≤ k ≤ 2,
所以 k的取值范围为[ 3,2]........................................................................12 分
21.【解析】(1)函数 f (x) 的定义域是{x | x R ,且 x 1},任取 x {x | x R ,且
x 1},............................................................................................................2 分
都有 f ( x)
| x | 1 | x | 1
( x)2
2 f (x), 1 x 1
f (x)是偶函数.................................................................................................4 分
(2 | x | 1 x 1 1)当 x 1时, f (x) 2 ,任取 x1, x2 (1, )2 ,且 x1 x ,x 1 x 1 x 1 2
则 f x1 f x2
1 1
x1 1 x2 1
x
2
x1
,x1 1 x2 1
1 x1 x2 , x1 1 0, x2 1 0 , x2 x1 0 ,
f x1 f x2 0,即 f x1 f x2 ,
f (x)在 (1, )上是减函数.............................................................................9 分
(3)由(1)(2)知函数 f (x) 在[ 4, 2] 上是增函数,
f (x) f ( 4) | 4 | 1 1 | 2 | 1 min 2 f (x)( 4) 1 3 , max
f ( 2) 1
( 2)2 1 ,
1
所求值域为 ,1 .........................................................................................12 分 3
22.【解析】(1)当 0 x 30 时,
y 500x 10x2 100x 2500 10x2 400x 2500 ;
x 30 10000当 时,y 500x 501x 4500 2500 2000
x 10000
x . x
10x2 400x 2500,0 x 30,
y 2000 x 10000 , x 30. ............................................................5 分
x
(2)当 0 x 30时, y 10(x 20)2 1500,
当 x 20 时, ymax 1500 ;.............................................................................8
分
当 x 30 y 2000 10000 时, x 2000 2 x
10000
2000 200 1800 ,
x x
当且仅当 x
10000
x ,即
x 100时取等号,....................................................11 分
1800 1500 ,
年产量为 100百件时,该企业获得利润最大,最大利润为 1800 万元.....12 分
同课章节目录
