2021-2022学年华东师大版八年级数学上册14.1.1 直角三角形三边的关系 同步测试题 (word版含答案)
文档属性
| 名称 | 2021-2022学年华东师大版八年级数学上册14.1.1 直角三角形三边的关系 同步测试题 (word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 196.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-28 13:41:50 | ||
图片预览


文档简介
14.1.1 直角三角形三边的关系同步测试题 2021-2022学年华东师大版八年级数学上册
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共13小题,共39分)
下列说法中正确的是( )
A. 已知,,分别是直角三角形的三边长,则必有
B. 直角三角形中,两条边的平方和等于第三边的平方
C. 在中,若,边,,的长分别是,,,则
D. 在中,若,,,分别是,,的对边,则
在RtABC中,BC=1,AC=2,B=,则AB的长是( )
A. B. C. D.
若一个直角三角形的两直角边的长分别为12和5,则第三边的长为( )
A. 或 B. 或 C. D.
如图,在正方形网格中,线段AB=,CD=,那么线段EF的长度为( )
A. B. C. D.
如图,在RtABC中,ACB=,BC=6,AC=8,则RtABC的斜边AB上的高CD的长是( )
A. B. C. D.
历史上对勾股定理的一种证法采用了如图所示的图形,其中两个全等的直角三角形的边AE,EB在一条直线上,证明中用到的面积相等关系是( )
A.
B.
C.
D.
“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b.若ab=8,大正方形的面积为25,则小正方形的边长为( )
A. B. C. D.
如图,每个小正方形的边长为1,ABC的三边a,b,c的大小关系是( )
A. B.
C. D.
一座建筑物发生了火灾,消防车到达现场后,发现最多只能靠近建筑物底端5米,消防车的云梯最大升长为13米,则云梯可以达该建筑物的最大高度是( )
A. 米 B. 米 C. 米 D. 米
如图,校园内有两棵树,相距8米,一棵树高13米,另一棵树高7米,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞( )
A. 米 B. 米 C. 米 D. 米
如图,在水塔O的东北方向32 m处有一抽水站A,在水塔的东南方向24 m处有一建筑工地B,在AB间建一条直水管,则水管的长为( )
A. B.
C. D.
如图是台阶的示意图.已知每个台阶的宽度都是30 cm,每个台阶的高度都是15 cm,则A点与B点之间的距离为( )
A. B.
C. D.
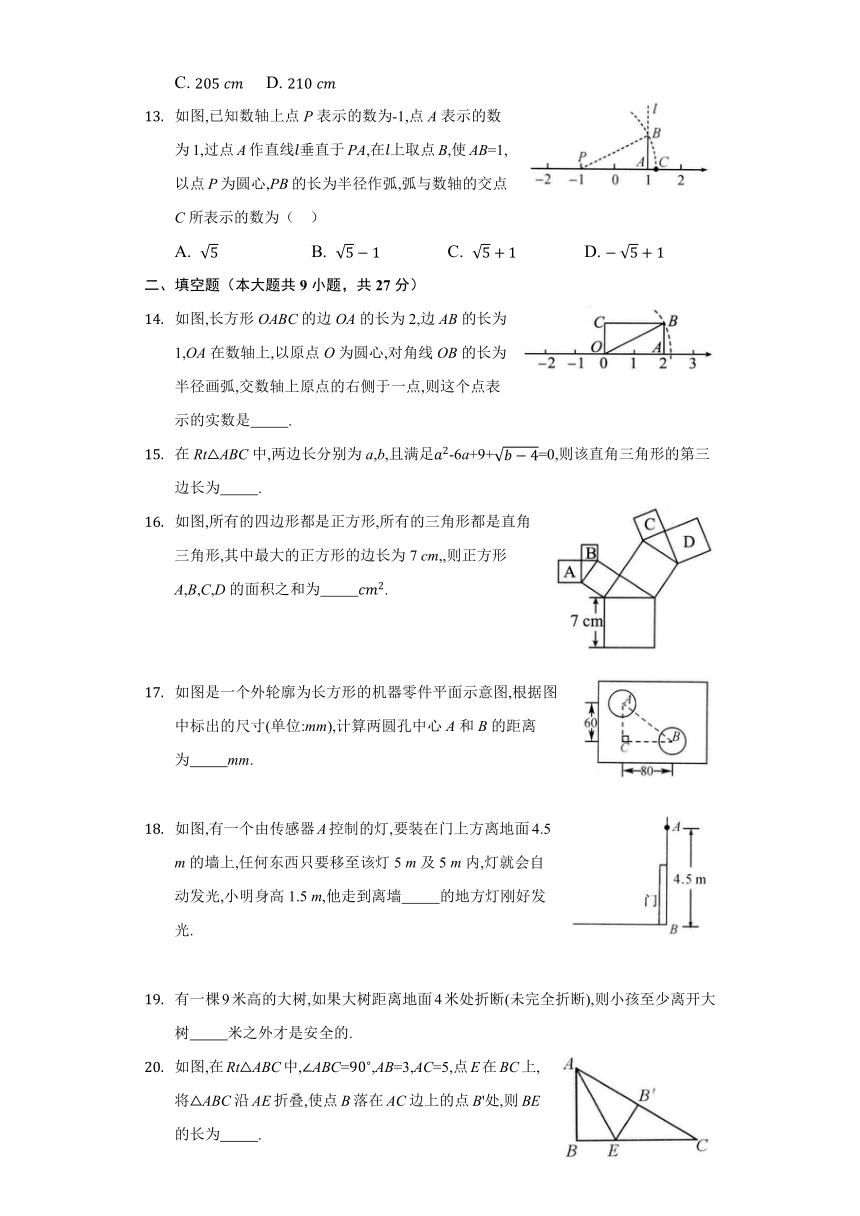
如图,已知数轴上点P表示的数为-1,点A表示的数为1,过点A作直线垂直于PA,在上取点B,使AB=1,以点P为圆心,PB的长为半径作弧,弧与数轴的交点C所表示的数为( )
A. B. C. D.
二、填空题(本大题共9小题,共27分)
如图,长方形OABC的边OA的长为2,边AB的长为1,OA在数轴上,以原点O为圆心,对角线OB的长为半径画弧,交数轴上原点的右侧于一点,则这个点表示的实数是 .
在RtABC中,两边长分别为a,b,且满足-6a+9+=0,则该直角三角形的第三边长为 .
如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7 cm,,则正方形A,B,C,D的面积之和为 .
如图是一个外轮廓为长方形的机器零件平面示意图,根据图中标出的尺寸(单位:mm),计算两圆孔中心A和B的距离为 mm.
如图,有一个由传感器A控制的灯,要装在门上方离地面4.5 m的墙上,任何东西只要移至该灯5 m及5 m内,灯就会自动发光,小明身高1.5 m,他走到离墙 的地方灯刚好发光.
有一棵9米高的大树,如果大树距离地面4米处折断(未完全折断),则小孩至少离开大树 米之外才是安全的.
如图,在RtABC中,ABC=,AB=3,AC=5,点E在BC上,将ABC沿AE折叠,使点B落在AC边上的点B'处,则BE的长为 .
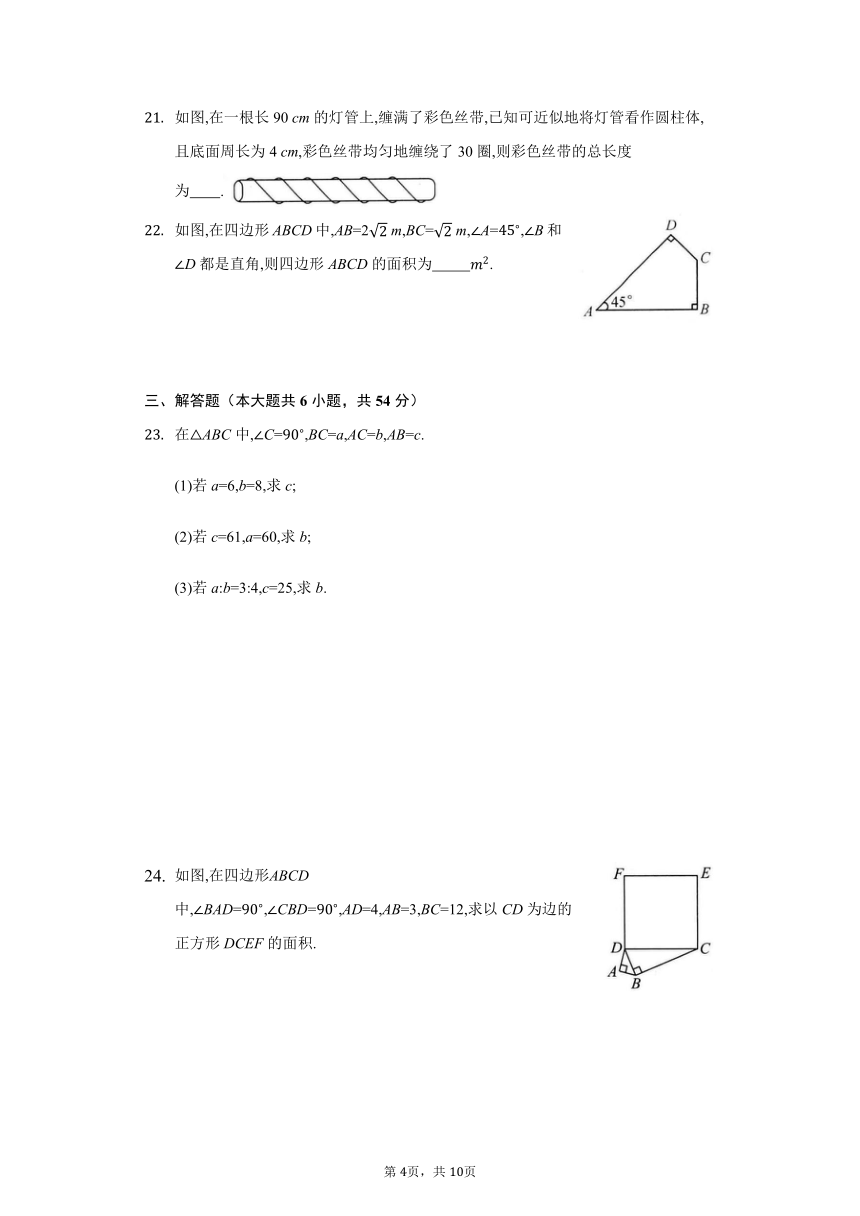
如图,在一根长90 cm的灯管上,缠满了彩色丝带,已知可近似地将灯管看作圆柱体,且底面周长为4 cm,彩色丝带均匀地缠绕了30圈,则彩色丝带的总长度为 .
如图,在四边形ABCD中,AB=2 m,BC= m,A=,B和D都是直角,则四边形ABCD的面积为 .
三、解答题(本大题共6小题,共54分)
在ABC中,C=,BC=a,AC=b,AB=c.
(1)若a=6,b=8,求c;
(2)若c=61,a=60,求b;
(3)若a:b=3:4,c=25,求b.
如图,在四边形ABCD中,BAD=,CBD=,AD=4,AB=3,BC=12,求以CD为边的正方形DCEF的面积.
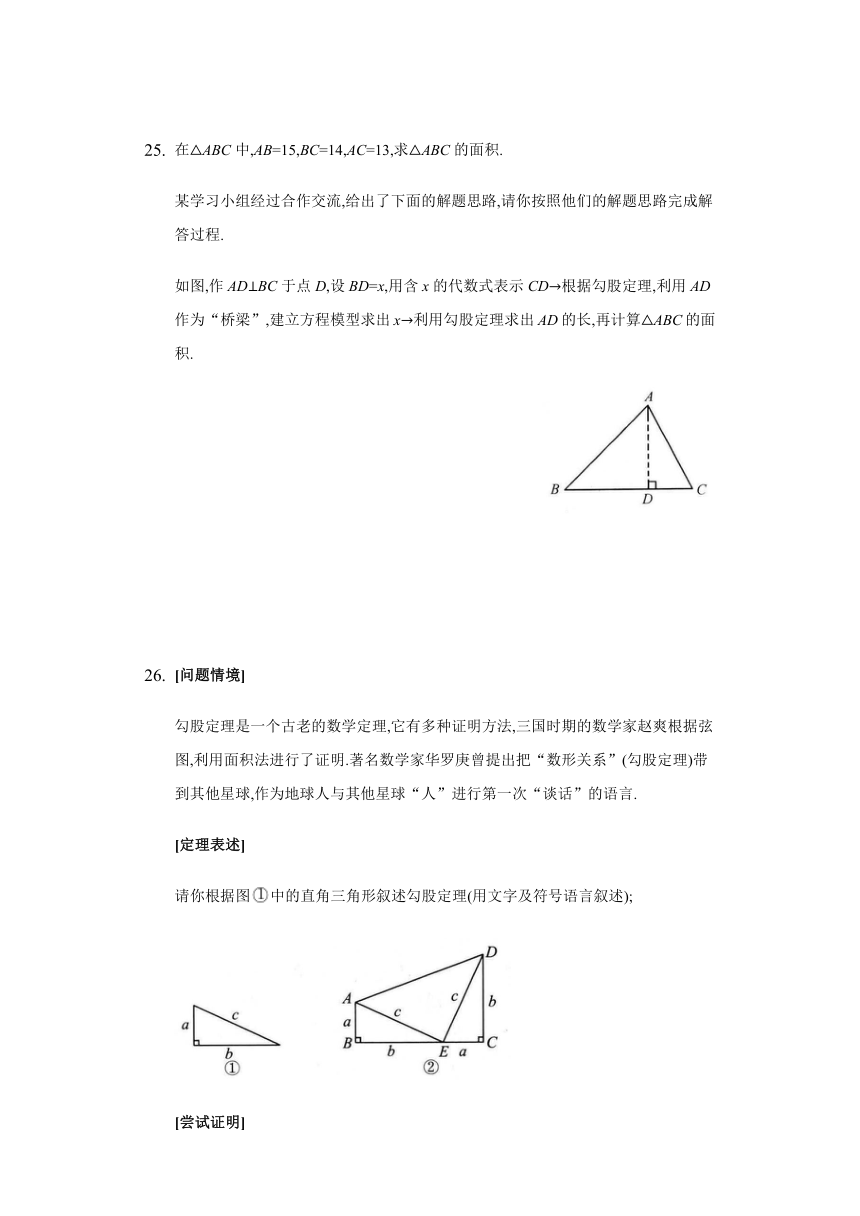
在ABC中,AB=15,BC=14,AC=13,求ABC的面积.
某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程.
如图,作ADBC于点D,设BD=x,用含x的代数式表示CD根据勾股定理,利用AD作为“桥梁”,建立方程模型求出x利用勾股定理求出AD的长,再计算ABC的面积.
[问题情境]
勾股定理是一个古老的数学定理,它有多种证明方法,三国时期的数学家赵爽根据弦图,利用面积法进行了证明.著名数学家华罗庚曾提出把“数形关系”(勾股定理)带到其他星球,作为地球人与其他星球“人”进行第一次“谈话”的语言.
[定理表述]
请你根据图中的直角三角形叙述勾股定理(用文字及符号语言叙述);
[尝试证明]
以图中的直角三角形为基础,可以拼成如图所示的图形,请你利用图,验证勾股定理;
[知识拓展]
利用图中的图形,我们可以证明<,其证明步骤如下:
BC=a+b,AD= ,
且在四边形ABCD中,有BC AD(填大小关系),即 ,
<.
“中华人民共和国道路交通管理条例”规定:小汽车在城市道路上行驶速度不得超过70 km/h.如图,一辆小汽车在一条城市街道上沿直线行驶,某一时刻刚好行驶到路对面车速检测仪A处的正前方30 m的C处,过了2 s后,测得小汽车与车速检测仪间距离为50 m,这辆小汽车超速了吗 (参考数据转换:1 m/s=3.6 km/h)
如图,一架云梯AB长为25米,顶端A靠在墙AC上,此时云梯底端B与墙角C距离为7米,云梯滑动后停在DE的位置上,测得AE长为4米,求云梯底端B在水平方向滑动了多少米
参考答案
1.【答案】D
2.【答案】D
3.【答案】C
4.【答案】D
5.【答案】B
6.【答案】D
7.【答案】D
8.【答案】C
9.【答案】A
10.【答案】C
11.【答案】B
12.【答案】A
13.【答案】B
14.【答案】
15.【答案】5或
16.【答案】49
17.【答案】100
18.【答案】4 m
19.【答案】3
20.【答案】
21.【答案】150 cm
22.【答案】
23.【答案】解:(1)10 (2)11 (3)20
24.【答案】解:
BAD=,
+=,
即+=,
BD=5.
CBD=,
+=,
即+=,
CD=13,
==169.
25.【答案】解:在ABC中,AB=15,BC=14,AC=13,设BD=x,则有CD=14-x,
由勾股定理,得=-=-,=-=-.
-=-.
解得x=9.
AD=12.
=BCAD=1412=84.
26.【答案】解:
[定理表述]
直角三角形两直角边的平方和等于斜边的平方.
即如果直角三角形的两直角边长分别为a,b,斜边长为c,那么+=.
[尝试证明]
RtABERtECD,
AEB=EDC.
又EDC+DEC=,
AEB+DEC=,
AED=.
=++,
(a+b)(a+b)=ab+ab+,
整理,得+=.
[知识拓展]
,<, a+b<.
27.【答案】解:在RtABC中,AC=30 m,AB=50 m,
根据勾股定理,得BC===40(m).
小汽车的速度v==20(m/s)=203.6(km/h)=72(km/h).
72 km/h>70 km/h,
这辆小汽车超速了.
28.【答案】解:在Rt△ABC中,AB=25米,BC=7米,
故AC===24米,
在Rt△ECD中,AB=DE=25米,
CE=AC-AE=24-4=20米,
故CD===15米,
BD=CD-BC=15-7=8(米).
答:云梯底端B在水平方向滑动了8米.
第2页,共3页
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共13小题,共39分)
下列说法中正确的是( )
A. 已知,,分别是直角三角形的三边长,则必有
B. 直角三角形中,两条边的平方和等于第三边的平方
C. 在中,若,边,,的长分别是,,,则
D. 在中,若,,,分别是,,的对边,则
在RtABC中,BC=1,AC=2,B=,则AB的长是( )
A. B. C. D.
若一个直角三角形的两直角边的长分别为12和5,则第三边的长为( )
A. 或 B. 或 C. D.
如图,在正方形网格中,线段AB=,CD=,那么线段EF的长度为( )
A. B. C. D.
如图,在RtABC中,ACB=,BC=6,AC=8,则RtABC的斜边AB上的高CD的长是( )
A. B. C. D.
历史上对勾股定理的一种证法采用了如图所示的图形,其中两个全等的直角三角形的边AE,EB在一条直线上,证明中用到的面积相等关系是( )
A.
B.
C.
D.
“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b.若ab=8,大正方形的面积为25,则小正方形的边长为( )
A. B. C. D.
如图,每个小正方形的边长为1,ABC的三边a,b,c的大小关系是( )
A. B.
C. D.
一座建筑物发生了火灾,消防车到达现场后,发现最多只能靠近建筑物底端5米,消防车的云梯最大升长为13米,则云梯可以达该建筑物的最大高度是( )
A. 米 B. 米 C. 米 D. 米
如图,校园内有两棵树,相距8米,一棵树高13米,另一棵树高7米,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞( )
A. 米 B. 米 C. 米 D. 米
如图,在水塔O的东北方向32 m处有一抽水站A,在水塔的东南方向24 m处有一建筑工地B,在AB间建一条直水管,则水管的长为( )
A. B.
C. D.
如图是台阶的示意图.已知每个台阶的宽度都是30 cm,每个台阶的高度都是15 cm,则A点与B点之间的距离为( )
A. B.
C. D.
如图,已知数轴上点P表示的数为-1,点A表示的数为1,过点A作直线垂直于PA,在上取点B,使AB=1,以点P为圆心,PB的长为半径作弧,弧与数轴的交点C所表示的数为( )
A. B. C. D.
二、填空题(本大题共9小题,共27分)
如图,长方形OABC的边OA的长为2,边AB的长为1,OA在数轴上,以原点O为圆心,对角线OB的长为半径画弧,交数轴上原点的右侧于一点,则这个点表示的实数是 .
在RtABC中,两边长分别为a,b,且满足-6a+9+=0,则该直角三角形的第三边长为 .
如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7 cm,,则正方形A,B,C,D的面积之和为 .
如图是一个外轮廓为长方形的机器零件平面示意图,根据图中标出的尺寸(单位:mm),计算两圆孔中心A和B的距离为 mm.
如图,有一个由传感器A控制的灯,要装在门上方离地面4.5 m的墙上,任何东西只要移至该灯5 m及5 m内,灯就会自动发光,小明身高1.5 m,他走到离墙 的地方灯刚好发光.
有一棵9米高的大树,如果大树距离地面4米处折断(未完全折断),则小孩至少离开大树 米之外才是安全的.
如图,在RtABC中,ABC=,AB=3,AC=5,点E在BC上,将ABC沿AE折叠,使点B落在AC边上的点B'处,则BE的长为 .
如图,在一根长90 cm的灯管上,缠满了彩色丝带,已知可近似地将灯管看作圆柱体,且底面周长为4 cm,彩色丝带均匀地缠绕了30圈,则彩色丝带的总长度为 .
如图,在四边形ABCD中,AB=2 m,BC= m,A=,B和D都是直角,则四边形ABCD的面积为 .
三、解答题(本大题共6小题,共54分)
在ABC中,C=,BC=a,AC=b,AB=c.
(1)若a=6,b=8,求c;
(2)若c=61,a=60,求b;
(3)若a:b=3:4,c=25,求b.
如图,在四边形ABCD中,BAD=,CBD=,AD=4,AB=3,BC=12,求以CD为边的正方形DCEF的面积.
在ABC中,AB=15,BC=14,AC=13,求ABC的面积.
某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程.
如图,作ADBC于点D,设BD=x,用含x的代数式表示CD根据勾股定理,利用AD作为“桥梁”,建立方程模型求出x利用勾股定理求出AD的长,再计算ABC的面积.
[问题情境]
勾股定理是一个古老的数学定理,它有多种证明方法,三国时期的数学家赵爽根据弦图,利用面积法进行了证明.著名数学家华罗庚曾提出把“数形关系”(勾股定理)带到其他星球,作为地球人与其他星球“人”进行第一次“谈话”的语言.
[定理表述]
请你根据图中的直角三角形叙述勾股定理(用文字及符号语言叙述);
[尝试证明]
以图中的直角三角形为基础,可以拼成如图所示的图形,请你利用图,验证勾股定理;
[知识拓展]
利用图中的图形,我们可以证明<,其证明步骤如下:
BC=a+b,AD= ,
且在四边形ABCD中,有BC AD(填大小关系),即 ,
<.
“中华人民共和国道路交通管理条例”规定:小汽车在城市道路上行驶速度不得超过70 km/h.如图,一辆小汽车在一条城市街道上沿直线行驶,某一时刻刚好行驶到路对面车速检测仪A处的正前方30 m的C处,过了2 s后,测得小汽车与车速检测仪间距离为50 m,这辆小汽车超速了吗 (参考数据转换:1 m/s=3.6 km/h)
如图,一架云梯AB长为25米,顶端A靠在墙AC上,此时云梯底端B与墙角C距离为7米,云梯滑动后停在DE的位置上,测得AE长为4米,求云梯底端B在水平方向滑动了多少米
参考答案
1.【答案】D
2.【答案】D
3.【答案】C
4.【答案】D
5.【答案】B
6.【答案】D
7.【答案】D
8.【答案】C
9.【答案】A
10.【答案】C
11.【答案】B
12.【答案】A
13.【答案】B
14.【答案】
15.【答案】5或
16.【答案】49
17.【答案】100
18.【答案】4 m
19.【答案】3
20.【答案】
21.【答案】150 cm
22.【答案】
23.【答案】解:(1)10 (2)11 (3)20
24.【答案】解:
BAD=,
+=,
即+=,
BD=5.
CBD=,
+=,
即+=,
CD=13,
==169.
25.【答案】解:在ABC中,AB=15,BC=14,AC=13,设BD=x,则有CD=14-x,
由勾股定理,得=-=-,=-=-.
-=-.
解得x=9.
AD=12.
=BCAD=1412=84.
26.【答案】解:
[定理表述]
直角三角形两直角边的平方和等于斜边的平方.
即如果直角三角形的两直角边长分别为a,b,斜边长为c,那么+=.
[尝试证明]
RtABERtECD,
AEB=EDC.
又EDC+DEC=,
AEB+DEC=,
AED=.
=++,
(a+b)(a+b)=ab+ab+,
整理,得+=.
[知识拓展]
,<, a+b<.
27.【答案】解:在RtABC中,AC=30 m,AB=50 m,
根据勾股定理,得BC===40(m).
小汽车的速度v==20(m/s)=203.6(km/h)=72(km/h).
72 km/h>70 km/h,
这辆小汽车超速了.
28.【答案】解:在Rt△ABC中,AB=25米,BC=7米,
故AC===24米,
在Rt△ECD中,AB=DE=25米,
CE=AC-AE=24-4=20米,
故CD===15米,
BD=CD-BC=15-7=8(米).
答:云梯底端B在水平方向滑动了8米.
第2页,共3页
