2021-2022学年华东师大版八年级数学上册14.2 勾股定理的应用同步测试题 (word版含答案)
文档属性
| 名称 | 2021-2022学年华东师大版八年级数学上册14.2 勾股定理的应用同步测试题 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 262.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-28 13:46:27 | ||
图片预览




文档简介
14.2 勾股定理的应用同步测试题 2021-2022学年华东师大版八年级数学上册
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共7小题,共21分)
如图,一圆柱体的底面周长为24 cm,高AB为9 cm,BC是直径,一只蚂蚁从点A出发沿着圆柱体的表面爬行到点C的最短路程是( )
A. B. C. D.
如图是一个三级台阶,它的每一级的长、宽、高分别为20 dm,3 dm,2 dm,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点的最短路程是( )
A. B. C. D.
一辆装满货物,宽为2.4米的卡车,欲通过如图所示的隧道,则卡车的外形高必须低于( )
A. 米 B. 米 C. 米 D. 米
如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米.如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,则小巷的宽度为( )
A. 米 B. 米 C. 米 D. 米
《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸,问门广几何 题目大意是:如图1、2(图2为图1的平面示意图),推开双门,双门间隙CD的距离为2寸,点C和点D距离门槛AB都为1尺(1尺=10寸),则AB的长是( )
A. 寸 B. 寸 C. 寸 D. 寸
在RtABC中,直角边AC=6, BC=8,将ABC按如图方式折叠,使点B与点A重合,折痕为DE,则CD的长为( )
A. B. C. D.
如图,圆柱的底面周长为6cm,AC是底面圆的直径,高BC=6cm,点P是竖直线段BC上一点,且PC=BC.一只蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离是( )
A. B.
C. D.
二、填空题(本大题共5小题,共15分)
如图,一圆柱形容器(厚度忽略不计),已知底面半径为6 m,高为16 cm,现将一根长度为28 cm的玻璃棒一端插入容器中,则玻璃棒露在容器外的长度的最小值是 cm.
我国古代数学著作《九章算术》中有这样一个问题:“今有池方一丈,葭(jiā)生其中央,出水一尺.引葭赴岸,适与岸齐.问水深几何 ”(注:丈、尺是长度单位,1丈=10尺)这段话翻译成现代汉语,即为:如图,有一个水池,水面是一个边长为1丈的正方形,在水池正中央有一根芦苇,它高出水面1尺.若把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,则水池里水的深度是 尺.
如图,在笔直的铁路上A、B两点相距25km,C、D为两村庄,DA=10km,CB=15km,DA⊥AB于A,CB⊥AB于B,现要在AB上建一个中转站E,使得C、D两村到E站的距离相等.则E应建在距A ______ km
如图,已知在ABC中,ABC=,AB=BC,三角形的顶点分别在相互平行的三条直线,,上,且相邻两平行线之间的距离均为1,则AC的长是 .
如图,在一款名为超级玛丽的游戏中,马里奥到达一个高为10米的高台A,利用旗杆顶部的绳索,划过90°到达与高台A水平距离为17米,高为3米的矮台B,马里奥在荡绳索过程中离地面的最低点的高度MN为 .
三、解答题(本大题共8小题,共64分)
学校要征收一块土地,形状如图所示,B=D=,AB=20 m,BC=15 m,CD=7 m,土地价格为1000元/,请你计算学校征收这块地需要多少钱
如图,一艘船由A港沿北偏东方向航行10 km至B港,然后再沿北偏西方向航行10 km至C港.
(1)求A,C两港之间的距离(结果保留到0.1 km,参考数据:1.414,1.732);
(2)确定C港在A港的什么方向.
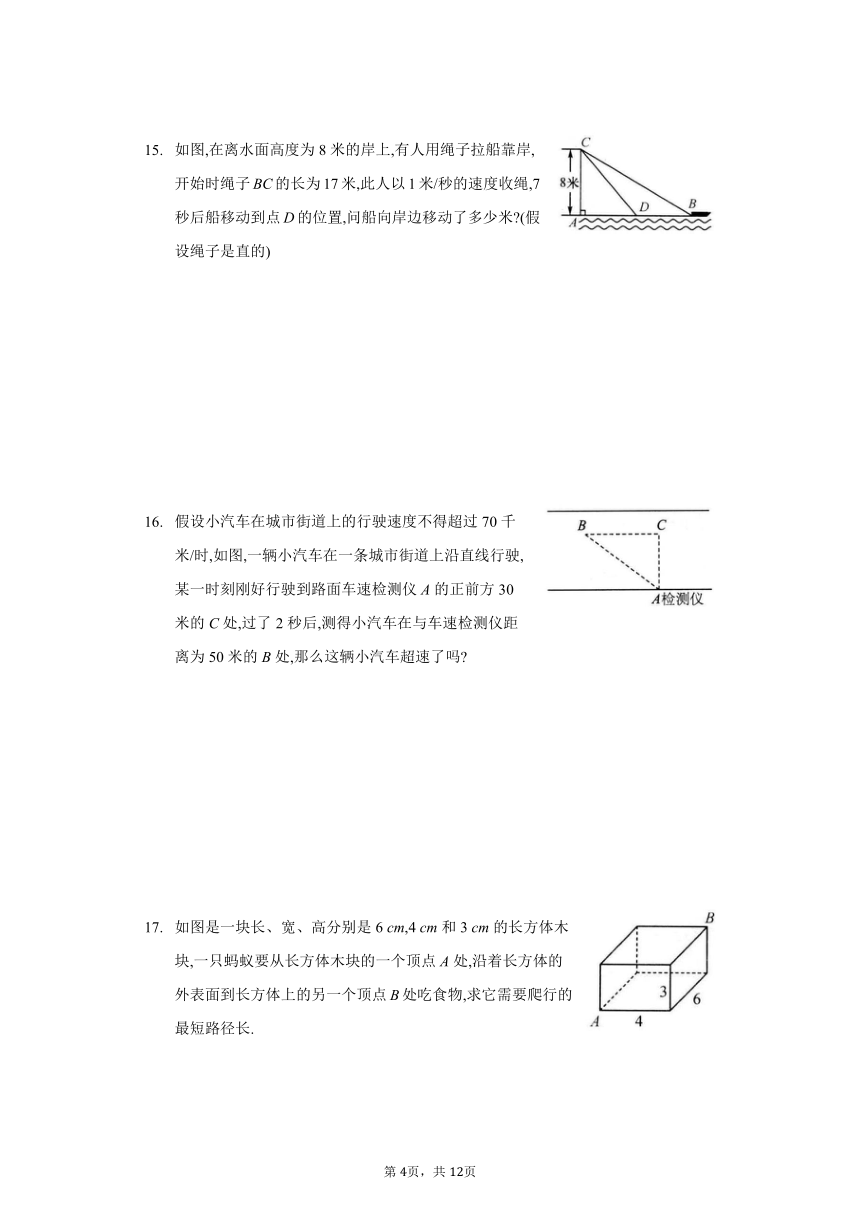
如图,在离水面高度为8米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为17米,此人以1米/秒的速度收绳,7秒后船移动到点D的位置,问船向岸边移动了多少米 (假设绳子是直的)
假设小汽车在城市街道上的行驶速度不得超过70千米/时,如图,一辆小汽车在一条城市街道上沿直线行驶,某一时刻刚好行驶到路面车速检测仪A的正前方30米的C处,过了2秒后,测得小汽车在与车速检测仪距离为50米的B处,那么这辆小汽车超速了吗
如图是一块长、宽、高分别是6 cm,4 cm和3 cm的长方体木块,一只蚂蚁要从长方体木块的一个顶点A处,沿着长方体的外表面到长方体上的另一个顶点B处吃食物,求它需要爬行的最短路径长.
如图,铁路MN和公路PQ在点O处交汇,公路PQ上距离点O240 m的A处与铁路MN的距离是120 m.如果火车行驶时,周围200 m以内会受到噪音的影响,那么火车在铁路MN上沿ON方向以72 km/h的速度行驶时,A处受噪音影响的时间是多少秒
如图,某沿海城市A接到台风警报,在该市正南方向120 km处有一台风中心正在B处形成,并沿着北偏东的方向以15 km/h的速度向点C移动.若在距台风中心150 km的区域内都将受到台风的影响,请问:
(1)画图计算说明:台风会影响到A市;
(2)画图计算说明:台风中心从B处出发后,经过几小时会影响到A市,对A市持续影响的时间是多少小时 经过几小时对A市的影响最大 [提示:=28800]
如下图,已知ABC中,B=,AB=16 cm,BC=12 cm,P,Q是ABC边上的两个动点,其中点P从点A开始沿AB方向运动,且速度为1 cm/s,点Q从点B开始沿BCA方向运动,且速度为2 cm/s,两点同时出发,设运动的时间为ts.
(1)出发2 s后,求PQ的长;
(2)当点Q在边BC上运动时,出发几秒后,PQB是等腰三角形
(3)当点Q在边CA上运动时,求能使BCQ是等腰三角形的运动时间.
参考答案
1.【答案】C
2.【答案】D
3.【答案】A
4.【答案】C
5.【答案】C
6.【答案】C
7.【答案】B
8.【答案】8
9.【答案】12
10.【答案】15
11.【答案】
12.【答案】2米
13.【答案】解:如图,连接AC.
在中,,,,
由勾股定理得:.则.
在中,,,
由勾股定理得:,则.
所以四边形的面积为:.
(元).
答:学校征收这块地需要234000元.
14.【答案】解:(1)A,C两港之间的距离约为14.1 km.
(2)C港在A港北偏东的方向上.
15.【答案】解:在Rt△ABC中,∵∠CAB=90°,BC=17米,AC=8米,
∴AB2=BC2-AC2=152,即AB=15米
∵此人以1米每秒的速度收绳,7秒后船移动到点D的位置,
∴CD=17-1×7=10(米),
∴AD2=CD2-AC2=62,即AD=6(米),
∴BD=AB-AD=15-6=9(米),
答:船向岸边移动了9米.
16.【答案】解:
在Rt△ABC中,AC=30m,AB=50m,
根据勾股定理可得:,
∴m,
∴小汽车的速度为v==20(m/s)=20×3.6(km/h)=72(km/h),
∵72(km/h)>70(km/h),
∴这辆小汽车超速了.
17.【答案】解:第一种情况:把我们所看到的长方体的正面和顶面展开,
则这个长方形的长和宽分别是9cm和4cm,
则所走的最短线段长是(cm);第二种情况:把长方体的左面与上面展开,
则这个长方形的长和宽分别是7cm和6cm,
所以走的最短线段是(cm);
第三种情况:把长方体的正面和右面展开,
则这个长方形的长和宽分别是10cm和3cm,
所以走的最短线段是(cm);
三种情况比较而言,第二种情况最短.
故蚂蚁需要爬行的最短路径的长为 cm.
18.【答案】解:如图:过点A作AC⊥ON,AB=AD=200米,
∵公路PQ上A处点距离O点240米,距离MN 120米,∴ AC=120米,
当火车到B点时对A处产生噪音影响,此时AB=200米,∵ AB=200米,AC=120米,
∴由勾股定理得:BC=160米,CD=160米,即BD=320米,
∵72千米/时=20米/秒,
∴受噪音影响的时间应是:320÷20=16秒,
答:A处受噪音影响的时间为16秒.
19.【答案】解:
(1)如图,过点A作ADBC于点D.
由题意得B=,
BAD=,则AD=BD.
+==,
AD=BD=120 km<150 km,
台风会影响到A市.
(2)如图,在BC上取两点E,F,使AE=AF=150 km.
在RtADE中,
DE===90(km),
BE=120-90=30(km).
=2(h),=12(h),=8(h),
台风中心从B处出发后,经过2 h会影响到A市,对A市持续影响的时间是12 h,经过8 h对A市的影响最大.
20.【答案】解:
(1)BQ=22=4(cm),
BP=AB-AP=16-21=14(cm),B=,
PQ===(cm).
(2)当点Q在边BC上运动时,若PQB是等腰三角形,则BQ=BP.
由题意,得BQ=2t cm,BP=(16-t)cm,
2t=16-t,
解得t=,
即当点Q在边BC上运动时,出发s后,PQB是等腰三角形.
(3)若CQ=BQ,如图(a)所示,
则C=CBQ.
ABC=,
CBQ+ABQ=,A+C=,
A=ABQ,
BQ=AQ,
CQ=AQ.
在RtABC中,由勾股定理,得AC==20(cm),
CQ=AQ=10(cm),
则BC+CQ=22(cm),
t=222=11.
若CQ=BC,如图(b)所示,
则BC+CQ=24(cm),
t=242=12.
若BC=BQ,如图(c)所示.
过点B作BEAC于点E,
则BE===(cm),
CE===(cm).
BC=BQ,BECQ,
CQ=2CE=14.4(cm),
则BC+CQ=26.4(cm),
t=26.42=13.2.
综上所述,当运动时间为11 s或12 s或13.2 s时,BCQ是等腰三角形.
第2页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共7小题,共21分)
如图,一圆柱体的底面周长为24 cm,高AB为9 cm,BC是直径,一只蚂蚁从点A出发沿着圆柱体的表面爬行到点C的最短路程是( )
A. B. C. D.
如图是一个三级台阶,它的每一级的长、宽、高分别为20 dm,3 dm,2 dm,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点的最短路程是( )
A. B. C. D.
一辆装满货物,宽为2.4米的卡车,欲通过如图所示的隧道,则卡车的外形高必须低于( )
A. 米 B. 米 C. 米 D. 米
如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米.如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,则小巷的宽度为( )
A. 米 B. 米 C. 米 D. 米
《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸,问门广几何 题目大意是:如图1、2(图2为图1的平面示意图),推开双门,双门间隙CD的距离为2寸,点C和点D距离门槛AB都为1尺(1尺=10寸),则AB的长是( )
A. 寸 B. 寸 C. 寸 D. 寸
在RtABC中,直角边AC=6, BC=8,将ABC按如图方式折叠,使点B与点A重合,折痕为DE,则CD的长为( )
A. B. C. D.
如图,圆柱的底面周长为6cm,AC是底面圆的直径,高BC=6cm,点P是竖直线段BC上一点,且PC=BC.一只蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离是( )
A. B.
C. D.
二、填空题(本大题共5小题,共15分)
如图,一圆柱形容器(厚度忽略不计),已知底面半径为6 m,高为16 cm,现将一根长度为28 cm的玻璃棒一端插入容器中,则玻璃棒露在容器外的长度的最小值是 cm.
我国古代数学著作《九章算术》中有这样一个问题:“今有池方一丈,葭(jiā)生其中央,出水一尺.引葭赴岸,适与岸齐.问水深几何 ”(注:丈、尺是长度单位,1丈=10尺)这段话翻译成现代汉语,即为:如图,有一个水池,水面是一个边长为1丈的正方形,在水池正中央有一根芦苇,它高出水面1尺.若把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面,则水池里水的深度是 尺.
如图,在笔直的铁路上A、B两点相距25km,C、D为两村庄,DA=10km,CB=15km,DA⊥AB于A,CB⊥AB于B,现要在AB上建一个中转站E,使得C、D两村到E站的距离相等.则E应建在距A ______ km
如图,已知在ABC中,ABC=,AB=BC,三角形的顶点分别在相互平行的三条直线,,上,且相邻两平行线之间的距离均为1,则AC的长是 .
如图,在一款名为超级玛丽的游戏中,马里奥到达一个高为10米的高台A,利用旗杆顶部的绳索,划过90°到达与高台A水平距离为17米,高为3米的矮台B,马里奥在荡绳索过程中离地面的最低点的高度MN为 .
三、解答题(本大题共8小题,共64分)
学校要征收一块土地,形状如图所示,B=D=,AB=20 m,BC=15 m,CD=7 m,土地价格为1000元/,请你计算学校征收这块地需要多少钱
如图,一艘船由A港沿北偏东方向航行10 km至B港,然后再沿北偏西方向航行10 km至C港.
(1)求A,C两港之间的距离(结果保留到0.1 km,参考数据:1.414,1.732);
(2)确定C港在A港的什么方向.
如图,在离水面高度为8米的岸上,有人用绳子拉船靠岸,开始时绳子BC的长为17米,此人以1米/秒的速度收绳,7秒后船移动到点D的位置,问船向岸边移动了多少米 (假设绳子是直的)
假设小汽车在城市街道上的行驶速度不得超过70千米/时,如图,一辆小汽车在一条城市街道上沿直线行驶,某一时刻刚好行驶到路面车速检测仪A的正前方30米的C处,过了2秒后,测得小汽车在与车速检测仪距离为50米的B处,那么这辆小汽车超速了吗
如图是一块长、宽、高分别是6 cm,4 cm和3 cm的长方体木块,一只蚂蚁要从长方体木块的一个顶点A处,沿着长方体的外表面到长方体上的另一个顶点B处吃食物,求它需要爬行的最短路径长.
如图,铁路MN和公路PQ在点O处交汇,公路PQ上距离点O240 m的A处与铁路MN的距离是120 m.如果火车行驶时,周围200 m以内会受到噪音的影响,那么火车在铁路MN上沿ON方向以72 km/h的速度行驶时,A处受噪音影响的时间是多少秒
如图,某沿海城市A接到台风警报,在该市正南方向120 km处有一台风中心正在B处形成,并沿着北偏东的方向以15 km/h的速度向点C移动.若在距台风中心150 km的区域内都将受到台风的影响,请问:
(1)画图计算说明:台风会影响到A市;
(2)画图计算说明:台风中心从B处出发后,经过几小时会影响到A市,对A市持续影响的时间是多少小时 经过几小时对A市的影响最大 [提示:=28800]
如下图,已知ABC中,B=,AB=16 cm,BC=12 cm,P,Q是ABC边上的两个动点,其中点P从点A开始沿AB方向运动,且速度为1 cm/s,点Q从点B开始沿BCA方向运动,且速度为2 cm/s,两点同时出发,设运动的时间为ts.
(1)出发2 s后,求PQ的长;
(2)当点Q在边BC上运动时,出发几秒后,PQB是等腰三角形
(3)当点Q在边CA上运动时,求能使BCQ是等腰三角形的运动时间.
参考答案
1.【答案】C
2.【答案】D
3.【答案】A
4.【答案】C
5.【答案】C
6.【答案】C
7.【答案】B
8.【答案】8
9.【答案】12
10.【答案】15
11.【答案】
12.【答案】2米
13.【答案】解:如图,连接AC.
在中,,,,
由勾股定理得:.则.
在中,,,
由勾股定理得:,则.
所以四边形的面积为:.
(元).
答:学校征收这块地需要234000元.
14.【答案】解:(1)A,C两港之间的距离约为14.1 km.
(2)C港在A港北偏东的方向上.
15.【答案】解:在Rt△ABC中,∵∠CAB=90°,BC=17米,AC=8米,
∴AB2=BC2-AC2=152,即AB=15米
∵此人以1米每秒的速度收绳,7秒后船移动到点D的位置,
∴CD=17-1×7=10(米),
∴AD2=CD2-AC2=62,即AD=6(米),
∴BD=AB-AD=15-6=9(米),
答:船向岸边移动了9米.
16.【答案】解:
在Rt△ABC中,AC=30m,AB=50m,
根据勾股定理可得:,
∴m,
∴小汽车的速度为v==20(m/s)=20×3.6(km/h)=72(km/h),
∵72(km/h)>70(km/h),
∴这辆小汽车超速了.
17.【答案】解:第一种情况:把我们所看到的长方体的正面和顶面展开,
则这个长方形的长和宽分别是9cm和4cm,
则所走的最短线段长是(cm);第二种情况:把长方体的左面与上面展开,
则这个长方形的长和宽分别是7cm和6cm,
所以走的最短线段是(cm);
第三种情况:把长方体的正面和右面展开,
则这个长方形的长和宽分别是10cm和3cm,
所以走的最短线段是(cm);
三种情况比较而言,第二种情况最短.
故蚂蚁需要爬行的最短路径的长为 cm.
18.【答案】解:如图:过点A作AC⊥ON,AB=AD=200米,
∵公路PQ上A处点距离O点240米,距离MN 120米,∴ AC=120米,
当火车到B点时对A处产生噪音影响,此时AB=200米,∵ AB=200米,AC=120米,
∴由勾股定理得:BC=160米,CD=160米,即BD=320米,
∵72千米/时=20米/秒,
∴受噪音影响的时间应是:320÷20=16秒,
答:A处受噪音影响的时间为16秒.
19.【答案】解:
(1)如图,过点A作ADBC于点D.
由题意得B=,
BAD=,则AD=BD.
+==,
AD=BD=120 km<150 km,
台风会影响到A市.
(2)如图,在BC上取两点E,F,使AE=AF=150 km.
在RtADE中,
DE===90(km),
BE=120-90=30(km).
=2(h),=12(h),=8(h),
台风中心从B处出发后,经过2 h会影响到A市,对A市持续影响的时间是12 h,经过8 h对A市的影响最大.
20.【答案】解:
(1)BQ=22=4(cm),
BP=AB-AP=16-21=14(cm),B=,
PQ===(cm).
(2)当点Q在边BC上运动时,若PQB是等腰三角形,则BQ=BP.
由题意,得BQ=2t cm,BP=(16-t)cm,
2t=16-t,
解得t=,
即当点Q在边BC上运动时,出发s后,PQB是等腰三角形.
(3)若CQ=BQ,如图(a)所示,
则C=CBQ.
ABC=,
CBQ+ABQ=,A+C=,
A=ABQ,
BQ=AQ,
CQ=AQ.
在RtABC中,由勾股定理,得AC==20(cm),
CQ=AQ=10(cm),
则BC+CQ=22(cm),
t=222=11.
若CQ=BC,如图(b)所示,
则BC+CQ=24(cm),
t=242=12.
若BC=BQ,如图(c)所示.
过点B作BEAC于点E,
则BE===(cm),
CE===(cm).
BC=BQ,BECQ,
CQ=2CE=14.4(cm),
则BC+CQ=26.4(cm),
t=26.42=13.2.
综上所述,当运动时间为11 s或12 s或13.2 s时,BCQ是等腰三角形.
第2页,共2页
