2021-2022学年人教版(2012)九年级数学上册24.4 弧长和扇形面积 课后培优练习 (word解析版)
文档属性
| 名称 | 2021-2022学年人教版(2012)九年级数学上册24.4 弧长和扇形面积 课后培优练习 (word解析版) |

|
|
| 格式 | docx | ||
| 文件大小 | 456.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-28 00:00:00 | ||
图片预览



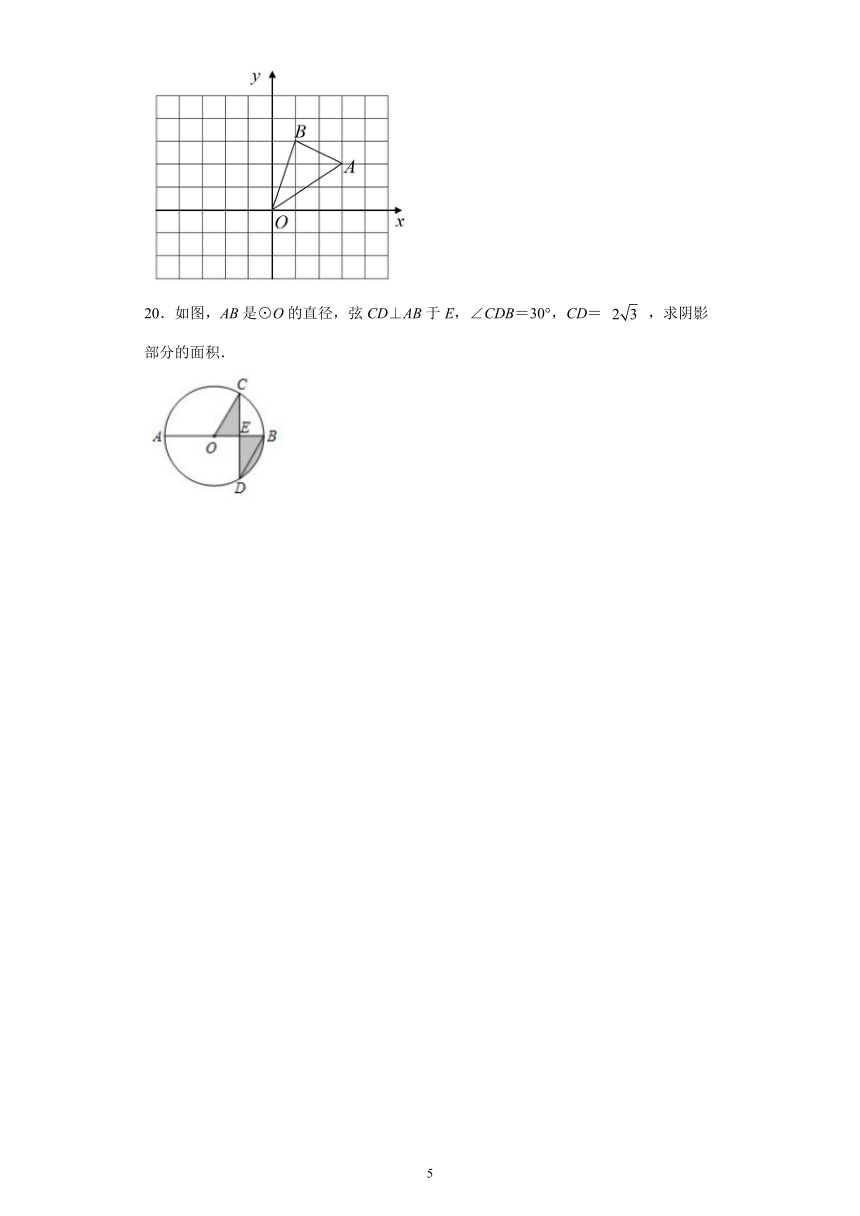
文档简介
24.4 弧长和扇形面积
一、单选题
1.已知圆锥的底面半径为5cm,母线长为10cm,则这个圆锥的全面积是( )
A.60πcm2 B.75πcm2 C.100πcm2 D.125πcm2
2.已知圆的直径,点在圆上,若,,则长为( )
A. B. C. D.
3.如图,以G(0,1)为圆心,半径为2的⊙G与x轴交于A、B两点,与y轴交于C、D两点,点E为⊙G上一动点,CF⊥AE于F,当点E从点B出发顺时针运动到点D时,点F所经过的路径长为( )
A.π B.π C.π D.π
4.已知圆锥的底面圆半径为3cm,母线长为5cm,则这个圆锥的侧面积是( )
A.15π cm2 B.15 cm2 C.30π cm2 D.30 cm2
5.已知圆心角为120°的扇形的面积为12π,则扇形的半径为( )
A.4 B.6 C. D.
6.如图,等腰△AOB中,顶角∠AOB=40°,用尺规按①到④的步骤操作:
①以O为圆心,OA为半径画圆;
②在⊙O上任取一点P(不与点A,B重合),连接AP;
③作AB的垂直平分线与⊙O交于M,N;
④作AP的垂直平分线与⊙O交于E,F.
结论Ⅰ:顺次连接M,E,N,F四点必能得到矩形;
结论Ⅱ:⊙O上只有唯一的点P,使得S扇形FOM=S扇形AOB.
对于结论Ⅰ和Ⅱ,下列判断正确的是( )
A.Ⅰ和Ⅱ都对 B.Ⅰ和Ⅱ都不对 C.Ⅰ不对Ⅱ对 D.Ⅰ对Ⅱ不对
7.已知圆的半径为3,扇形的圆心角为120°.则扇形的弧长为( )
A. B. C. D.
8.如图,点A、B、C、D都在边长为1的网格格点上,以A为圆心,AE为半径画弧,弧EF经过格点D,则扇形AEF的面积是( )
A. B. C.π D.
9.如图,在△ABC中,∠ACB=90°,AC=BC,AB=4cm,CD是中线,点E、F同时从点D出发,以相同的速度分别沿DC、DB方向移动,当点E到达点C时,运动停止,直线AE分别与CF、BC相交于G、H,则在点E、F移动过程中,点G移动路线的长度为( )
A.2 B.π C.2π D.π
10.已知一个扇形的半径长是,圆心角为,则这个扇形的面积为( )
A. B.
C. D.
11.如图, ABCD中,∠C=110°,AB=2,以AB为直径的⊙O交BC于点E,则的长为( )
A. B. C. D.
二、填空题
12.如图Rt△ABC,∠C=90°,分别以各边为直径作半圆,图中阴影部分在数学史上称为“希波克拉底月牙”:当AC=4,BC=6时,则阴影部分的面积为 ___.
13.已知扇形的半径为2 ,圆心角为60°,则它的面积为________.
14.如图,在扇形中,,,若以点为圆心,为半径画弧,与交于点,则图中阴影部分的面积和是_________.
15.如图,在⊙O中,直径AB=4,C是⊙O上一点,∠CAB=30°,则的长为________.
16.某扇形的圆心角是45°,面积为,该扇形的弧长是______.
三、解答题
17.(1)如图,用尺规在原图上作出⊙O的内接等边△ABC;(不写作法,保留作图痕迹)
(2)在(1)所作的图形中,若⊙O半径为6,求的长及扇形AOB的面积.
18.如图,⊙O半径为10cm,AB是⊙O的一条弦且∠AOB=60°,求图中阴影部分的面积.
19.如图,在边长为1的正方形组成的网格中建立直角坐标系,的顶点均在格点上,点O为原点,点A,B的坐标分别是、.
(1)将向下平移3个单位后得到,则点的坐标为________;
(2)将绕点O逆时针旋转90°后得到,请在图中作出,并求出这时点的坐标为________;
(3)在(2)中的旋转过程中,求出线段扫过的图形的弧长.
20.如图,AB是⊙O的直径,弦CD⊥AB于E,∠CDB=30°,CD= ,求阴影部分的面积.
试卷第1页,共3页
参考答案
1.B
解:圆锥的侧面积,圆锥的底面积
∴这个圆锥的全面积=.
故选B.
2.B
解:,,
,
,
,
,
的长为:.
故选:B.
3.A
连接AC,取其中点H,则点F的运动轨迹是以H为圆心,以HA为半径的圆的上,
∵以G(0,1)为圆心,半径为2的⊙G与x轴交于A、B两点,与y轴交于C、D两点,
∴OG=1,GA=GC=2,OC=3,
∵∠AOG=90°,
∴OG=1,GA=GC=2,
∴OA==,AC==2,
∴HA=,
∴∠HCO=30°,
∴∠AHO=60°,
∴点F所经过的路径长为=π,
故选A.
4.A
解:圆锥的侧面积cm2,
故选:A.
5.B
解:∵圆心角为120°的扇形的面积为12π,
∴,
解得r=6或r=-6(舍去),
故选B.
6.D
解:如图,连接,,..
垂直平分,垂直平分,由“垂径定理的逆定理”可知,和都是的直径,
,,
四边形是平行四边形,
,
四边形是矩形,故(Ⅰ)正确,
观察图形可知当,
,
观察图形可知,这样的点不唯一(如下图所示),故(Ⅱ)错误,
故选:D.
7.B
解:扇形的弧长为 .
故选:B
8.A
依题意,点A、B、C、D都在边长为1的网格格点上,
,,
扇形AEF的面积.
故选A.
9.D
【详解】
解:如图,
∵CA=CB,∠ACB=90°,AD=DB,
∴CD⊥AB,
∴∠ADE=∠CDF=90°,CD=AD=DB,
在△ADE和△CDF中,
,
∴△ADE≌△CDF(SAS),
∴∠DAE=∠DCF,
∵∠AED=∠CEG,
∴∠ADE=∠CGE=90°,
∴A、C、G、D四点共圆,
∴点G的运动轨迹为弧CD,
∵AB=4,ABAC,
∴AC=2,
∴OA=OC,
∵DA=DC,OA=OC,
∴DO⊥AC,
∴∠DOC=90°,
∴点G的运动轨迹的长为π.
故选:D.
10.B
解:由扇形的面积公式可得,这个扇形的面积为
故选B
11.C
解:连接OE,如图:
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠B+∠C=180°,
∵∠C=110°,
∴∠B=70°,
∵OB=OE,
∴∠B=∠OEB,
∴∠OEB=70°,
∴∠AOE=∠B+∠OEB=70°+70°=140°,
∵AB=2,AB为⊙O的直径,
∴OA=OB=OE=1,
∴的长为:,
故选:C.
12.12
解:在中,,AC=4,BC=6
∴
则阴影部分的面积
故答案为12
13.##
解:扇形的面积是:,
故答案为:.
14.
解:连接,
由已知可得,
又已知,
∴,
∴为等边三角形,
∴,
∴,
∵,
∴,
∴阴影面积为,
故答案为:.
15.
如图,连接OC,
∵∠CAB=30°,
∴∠BOC=2∠CAB=60°,
∵AB=4,
∴OB=2,
∴的长是:.
故答案是:.
16.
解:设该扇形的半径为R,
解得,,
则该扇形的弧长是:,
故答案为:.
17.(1)见解析;(2),.
(1)如图所示,△ABC即为所求.
(2)如图所示:∵△ABC为等边三角形,
∴∠ACB=60°,
∴∠AOB=120°,
∵AO=BO=6,
∴,.
18.
如图,作于点C.
由圆的基本性质可知,
∵,
∴为等边三角形,
∴,.
在中,,
∴,
∴,
∴.
∵,
∴.
19.(1)见解析,(1,0),(2)见解析,(﹣2,3)(3)
解:(1)如图,△A1O1B1为所作,点B1的坐标为(1,0);
故答案为:(1,0);
(2)如图,△A2OB2为所作,点A2的坐标为(﹣2,3);
故答案为:(﹣2,3);
(3)如图,OA==,
而∠AOA2=90°,所以线段OA扫过的弧长为==.
20.
解:连接OD.
∵CD⊥AB,
∴CE=DE=CD=(垂径定理),弧BC=弧BD
故S△OCE=S△ODE,∠COB=∠DOB,
∴S阴=S扇形OBD ,
又∵∠CDB=30°,
∴∠COB=∠DOB=60°(圆周角定理),
∴∠OCB=30°
∴OC=,
解得:,
故S扇形OBD= =,
即阴影部分的面积为.
答案第1页,共2页
一、单选题
1.已知圆锥的底面半径为5cm,母线长为10cm,则这个圆锥的全面积是( )
A.60πcm2 B.75πcm2 C.100πcm2 D.125πcm2
2.已知圆的直径,点在圆上,若,,则长为( )
A. B. C. D.
3.如图,以G(0,1)为圆心,半径为2的⊙G与x轴交于A、B两点,与y轴交于C、D两点,点E为⊙G上一动点,CF⊥AE于F,当点E从点B出发顺时针运动到点D时,点F所经过的路径长为( )
A.π B.π C.π D.π
4.已知圆锥的底面圆半径为3cm,母线长为5cm,则这个圆锥的侧面积是( )
A.15π cm2 B.15 cm2 C.30π cm2 D.30 cm2
5.已知圆心角为120°的扇形的面积为12π,则扇形的半径为( )
A.4 B.6 C. D.
6.如图,等腰△AOB中,顶角∠AOB=40°,用尺规按①到④的步骤操作:
①以O为圆心,OA为半径画圆;
②在⊙O上任取一点P(不与点A,B重合),连接AP;
③作AB的垂直平分线与⊙O交于M,N;
④作AP的垂直平分线与⊙O交于E,F.
结论Ⅰ:顺次连接M,E,N,F四点必能得到矩形;
结论Ⅱ:⊙O上只有唯一的点P,使得S扇形FOM=S扇形AOB.
对于结论Ⅰ和Ⅱ,下列判断正确的是( )
A.Ⅰ和Ⅱ都对 B.Ⅰ和Ⅱ都不对 C.Ⅰ不对Ⅱ对 D.Ⅰ对Ⅱ不对
7.已知圆的半径为3,扇形的圆心角为120°.则扇形的弧长为( )
A. B. C. D.
8.如图,点A、B、C、D都在边长为1的网格格点上,以A为圆心,AE为半径画弧,弧EF经过格点D,则扇形AEF的面积是( )
A. B. C.π D.
9.如图,在△ABC中,∠ACB=90°,AC=BC,AB=4cm,CD是中线,点E、F同时从点D出发,以相同的速度分别沿DC、DB方向移动,当点E到达点C时,运动停止,直线AE分别与CF、BC相交于G、H,则在点E、F移动过程中,点G移动路线的长度为( )
A.2 B.π C.2π D.π
10.已知一个扇形的半径长是,圆心角为,则这个扇形的面积为( )
A. B.
C. D.
11.如图, ABCD中,∠C=110°,AB=2,以AB为直径的⊙O交BC于点E,则的长为( )
A. B. C. D.
二、填空题
12.如图Rt△ABC,∠C=90°,分别以各边为直径作半圆,图中阴影部分在数学史上称为“希波克拉底月牙”:当AC=4,BC=6时,则阴影部分的面积为 ___.
13.已知扇形的半径为2 ,圆心角为60°,则它的面积为________.
14.如图,在扇形中,,,若以点为圆心,为半径画弧,与交于点,则图中阴影部分的面积和是_________.
15.如图,在⊙O中,直径AB=4,C是⊙O上一点,∠CAB=30°,则的长为________.
16.某扇形的圆心角是45°,面积为,该扇形的弧长是______.
三、解答题
17.(1)如图,用尺规在原图上作出⊙O的内接等边△ABC;(不写作法,保留作图痕迹)
(2)在(1)所作的图形中,若⊙O半径为6,求的长及扇形AOB的面积.
18.如图,⊙O半径为10cm,AB是⊙O的一条弦且∠AOB=60°,求图中阴影部分的面积.
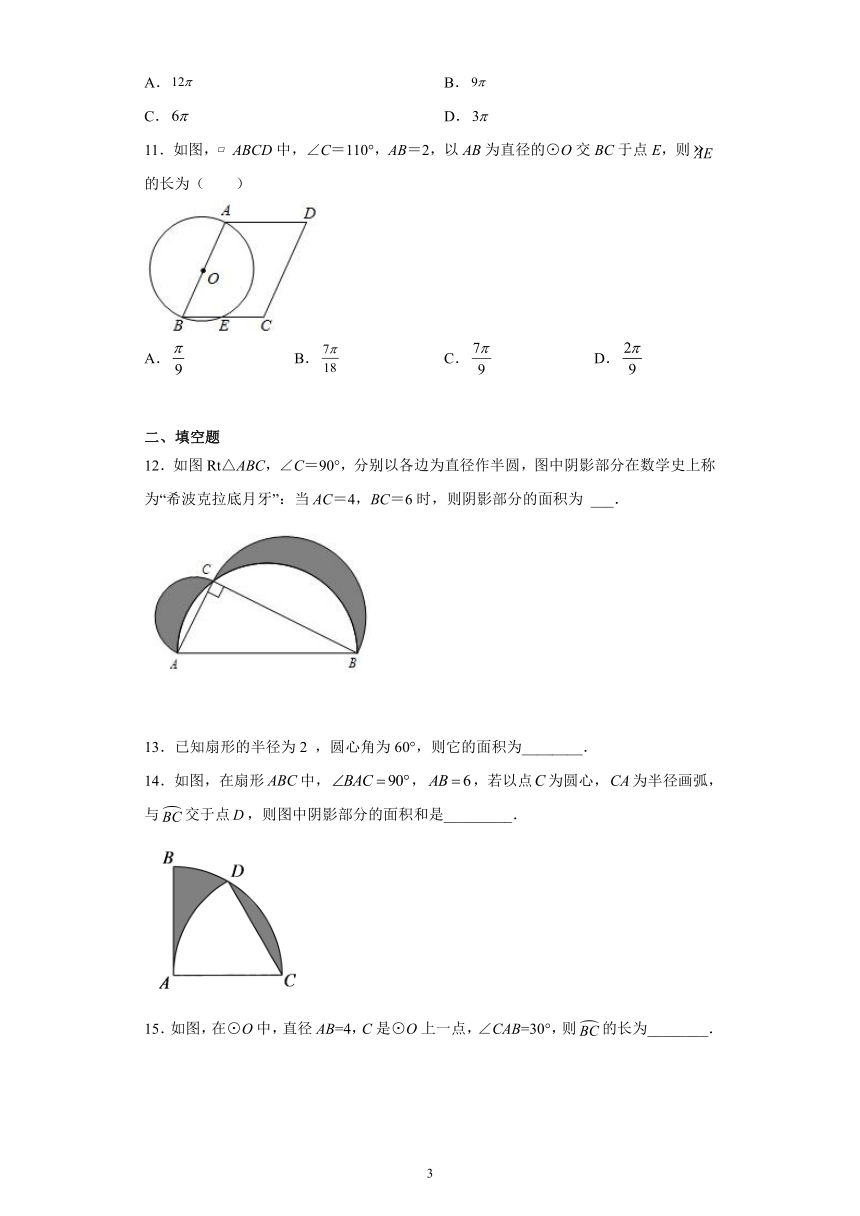
19.如图,在边长为1的正方形组成的网格中建立直角坐标系,的顶点均在格点上,点O为原点,点A,B的坐标分别是、.
(1)将向下平移3个单位后得到,则点的坐标为________;
(2)将绕点O逆时针旋转90°后得到,请在图中作出,并求出这时点的坐标为________;
(3)在(2)中的旋转过程中,求出线段扫过的图形的弧长.
20.如图,AB是⊙O的直径,弦CD⊥AB于E,∠CDB=30°,CD= ,求阴影部分的面积.
试卷第1页,共3页
参考答案
1.B
解:圆锥的侧面积,圆锥的底面积
∴这个圆锥的全面积=.
故选B.
2.B
解:,,
,
,
,
,
的长为:.
故选:B.
3.A
连接AC,取其中点H,则点F的运动轨迹是以H为圆心,以HA为半径的圆的上,
∵以G(0,1)为圆心,半径为2的⊙G与x轴交于A、B两点,与y轴交于C、D两点,
∴OG=1,GA=GC=2,OC=3,
∵∠AOG=90°,
∴OG=1,GA=GC=2,
∴OA==,AC==2,
∴HA=,
∴∠HCO=30°,
∴∠AHO=60°,
∴点F所经过的路径长为=π,
故选A.
4.A
解:圆锥的侧面积cm2,
故选:A.
5.B
解:∵圆心角为120°的扇形的面积为12π,
∴,
解得r=6或r=-6(舍去),
故选B.
6.D
解:如图,连接,,..
垂直平分,垂直平分,由“垂径定理的逆定理”可知,和都是的直径,
,,
四边形是平行四边形,
,
四边形是矩形,故(Ⅰ)正确,
观察图形可知当,
,
观察图形可知,这样的点不唯一(如下图所示),故(Ⅱ)错误,
故选:D.
7.B
解:扇形的弧长为 .
故选:B
8.A
依题意,点A、B、C、D都在边长为1的网格格点上,
,,
扇形AEF的面积.
故选A.
9.D
【详解】
解:如图,
∵CA=CB,∠ACB=90°,AD=DB,
∴CD⊥AB,
∴∠ADE=∠CDF=90°,CD=AD=DB,
在△ADE和△CDF中,
,
∴△ADE≌△CDF(SAS),
∴∠DAE=∠DCF,
∵∠AED=∠CEG,
∴∠ADE=∠CGE=90°,
∴A、C、G、D四点共圆,
∴点G的运动轨迹为弧CD,
∵AB=4,ABAC,
∴AC=2,
∴OA=OC,
∵DA=DC,OA=OC,
∴DO⊥AC,
∴∠DOC=90°,
∴点G的运动轨迹的长为π.
故选:D.
10.B
解:由扇形的面积公式可得,这个扇形的面积为
故选B
11.C
解:连接OE,如图:
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠B+∠C=180°,
∵∠C=110°,
∴∠B=70°,
∵OB=OE,
∴∠B=∠OEB,
∴∠OEB=70°,
∴∠AOE=∠B+∠OEB=70°+70°=140°,
∵AB=2,AB为⊙O的直径,
∴OA=OB=OE=1,
∴的长为:,
故选:C.
12.12
解:在中,,AC=4,BC=6
∴
则阴影部分的面积
故答案为12
13.##
解:扇形的面积是:,
故答案为:.
14.
解:连接,
由已知可得,
又已知,
∴,
∴为等边三角形,
∴,
∴,
∵,
∴,
∴阴影面积为,
故答案为:.
15.
如图,连接OC,
∵∠CAB=30°,
∴∠BOC=2∠CAB=60°,
∵AB=4,
∴OB=2,
∴的长是:.
故答案是:.
16.
解:设该扇形的半径为R,
解得,,
则该扇形的弧长是:,
故答案为:.
17.(1)见解析;(2),.
(1)如图所示,△ABC即为所求.
(2)如图所示:∵△ABC为等边三角形,
∴∠ACB=60°,
∴∠AOB=120°,
∵AO=BO=6,
∴,.
18.
如图,作于点C.
由圆的基本性质可知,
∵,
∴为等边三角形,
∴,.
在中,,
∴,
∴,
∴.
∵,
∴.
19.(1)见解析,(1,0),(2)见解析,(﹣2,3)(3)
解:(1)如图,△A1O1B1为所作,点B1的坐标为(1,0);
故答案为:(1,0);
(2)如图,△A2OB2为所作,点A2的坐标为(﹣2,3);
故答案为:(﹣2,3);
(3)如图,OA==,
而∠AOA2=90°,所以线段OA扫过的弧长为==.
20.
解:连接OD.
∵CD⊥AB,
∴CE=DE=CD=(垂径定理),弧BC=弧BD
故S△OCE=S△ODE,∠COB=∠DOB,
∴S阴=S扇形OBD ,
又∵∠CDB=30°,
∴∠COB=∠DOB=60°(圆周角定理),
∴∠OCB=30°
∴OC=,
解得:,
故S扇形OBD= =,
即阴影部分的面积为.
答案第1页,共2页
同课章节目录
