2021-2022学年华东师大版八年级数学上册第14章 勾股定理 同步测试题 (word版含答案)
文档属性
| 名称 | 2021-2022学年华东师大版八年级数学上册第14章 勾股定理 同步测试题 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 186.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-28 13:51:32 | ||
图片预览


文档简介
第14章勾股定理同步测试题 2021-2022学年华东师大版八年级数学上册
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共10小题,共30分)
已知ABC的三边长分别为5,13,12,则ABC的面积为( )
A. B. C. D. 不能确定
由下列条件能判定ABC为直角三角形的是( )
A. B.
C. ,, D.
用反证法证明:a,b至少有一个为0,应该假设( )
A. ,都不为 B. ,只有一个为
C. ,至多一个为 D. ,都为
如图,点D在ABC的边AC上,将ABC沿BD翻折后,点A恰好与点C重合.若BC=5,CD=3,则BD的长为( )
A. B. C. D.
如图,两个较大正方形的面积分别为225,289,则字母A所代表的正方形的面积为( )
A. B. C. D.
如图,在44的方格纸中,有一个格点三角形ABC,关于它的描述正确的是( )
A. 三边长都是有理数 B. 是等腰三角形
C. 是直角三角形 D. 有一条边长为
将一根长度为16 cm自然伸直的弹性皮筋AB两端固定在水平的桌面上,然后把中点C竖直向上拉升6 cm至D点(如图),则该弹性皮筋被拉长了( )
A. B. C. D.
如图,在ABC中,B=,两直角边AB=7,BC=24,在三角形内有一点P到各边的距离相等,则这个距离是( )
A. B. C. D.
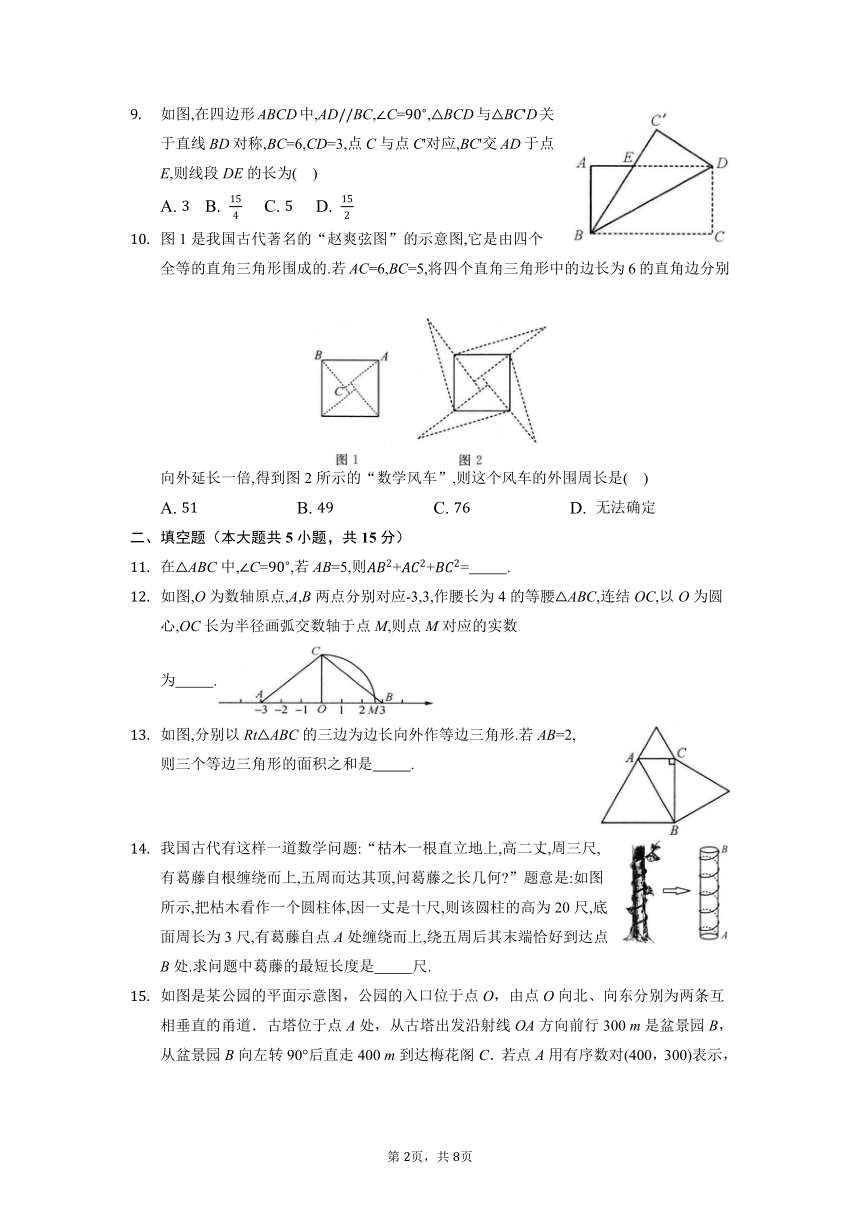
如图,在四边形ABCD中,ADBC,C=,BCD与BC'D关于直线BD对称,BC=6,CD=3,点C与点C'对应,BC'交AD于点E,则线段DE的长为( )
A. B. C. D.
图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=6,BC=5,将四个直角三角形中的边长为6的直角边分别向外延长一倍,得到图2所示的“数学风车”,则这个风车的外围周长是( )
A. B. C. D. 无法确定
二、填空题(本大题共5小题,共15分)
在ABC中,C=,若AB=5,则++= .
如图,O为数轴原点,A,B两点分别对应-3,3,作腰长为4的等腰ABC,连结OC,以O为圆心,OC长为半径画弧交数轴于点M,则点M对应的实数为 .
如图,分别以RtABC的三边为边长向外作等边三角形.若AB=2,则三个等边三角形的面积之和是 .
我国古代有这样一道数学问题:“枯木一根直立地上,高二丈,周三尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何 ”题意是:如图所示,把枯木看作一个圆柱体,因一丈是十尺,则该圆柱的高为20尺,底面周长为3尺,有葛藤自点A处缠绕而上,绕五周后其末端恰好到达点B处.求问题中葛藤的最短长度是 尺.
如图是某公园的平面示意图,公园的入口位于点O,由点O向北、向东分别为两条互相垂直的甬道.古塔位于点A处,从古塔出发沿射线OA方向前行300 m是盆景园B,从盆景园B向左转90°后直走400 m到达梅花阁C.若点A用有序数对(400,300)表示,则点C可表示为________.
三、解答题(本大题共8小题,共75分)
如图,在ABC中,AC=5,BC=12,AB=13,D是BC的中点,求AD的长和ABD的面积.
已知:A,B,C是ABC的内角.用反证法证明:A,B,C中至少有一个角大于或等于.
如图,AC=BC=BD=1,AD=,求ABD的面积.
已知a,b,c满足++|c-|=0.
(1)求a,b,c的值;
(2)试问以a,b,c为边能否构成直角三角形 请说明理由.
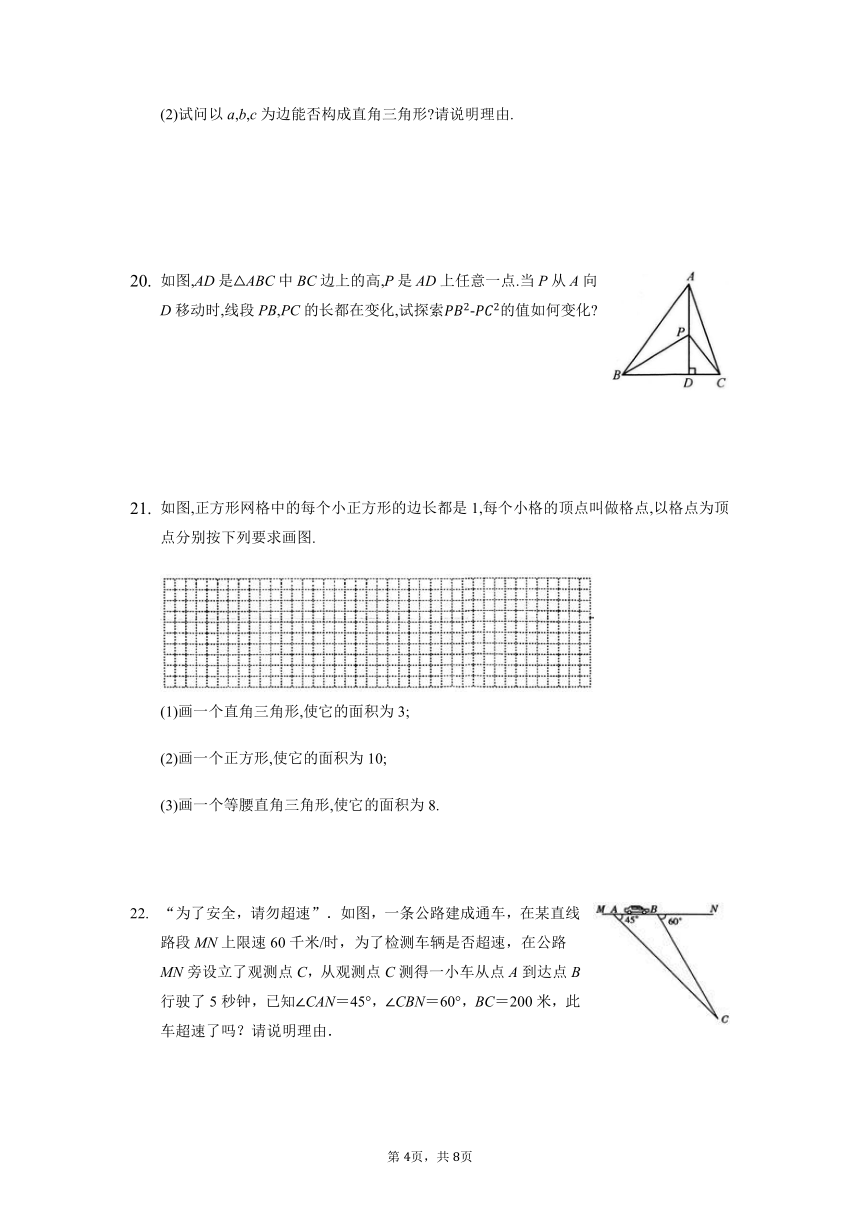
如图,AD是ABC中BC边上的高,P是AD上任意一点.当P从A向D移动时,线段PB,PC的长都在变化,试探索-的值如何变化
如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画图.
(1)画一个直角三角形,使它的面积为3;
(2)画一个正方形,使它的面积为10;
(3)画一个等腰直角三角形,使它的面积为8.
“为了安全,请勿超速”.如图,一条公路建成通车,在某直线路段MN上限速60千米/时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.
如图,在ABC中,ACB=,AB=10 cm,BC=6 cm.若点P从点A出发,以每秒1 cm的速度沿折线A-C-B-A运动,设运动时间为t s(t>0).
(1)若点P在AC上,且满足PA=PB时,求出此时t的值;
(2)若点P恰好在BAC的平分线上(但不与A点重合),求t的值.
参考答案
1.【答案】A
2.【答案】A
3.【答案】A
4.【答案】D
5.【答案】D
6.【答案】D
7.【答案】B
8.【答案】B
9.【答案】B
10.【答案】C
11.【答案】50
12.【答案】
13.【答案】2
14.【答案】25
15.【答案】(400,800)
16.【答案】解:AD=,=15.
17.【答案】证明:假设A,B,C都小于,
即A<,B<,C<,
则A+B+C<.
这与“三角形的内角和等于”矛盾,
所以假设不成立.
因此,A,B,C中至少有一个角大于或等于.
18.【答案】解:=ABBD=.
19.【答案】解:(1)++|c-|=0,
a-=0,b-3=0,c-=0.
a=,b=3,c=.
(2)能构成直角三角形.
理由:
∵b2=9=a2+c2,
∴以a,b,c为边的三角形是直角三角形.
20.【答案】解:-的值不变.
理由:ADBC,ADB=ADC=.
根据勾股定理,得=+,=+.
-=+-(+)=-.
-的值不变,
-的值不变.
21.【答案】解:(1)如图.
(2)如图.
(3)如图.
22.【答案】解:此车没有超速.
理由:过C作CH⊥MN于H,
∵∠CBN=60°,BC=200米,
∴∠HCB=30°,
∴BH===100(米),
,
即(米),
∵∠CAN=45°,
∴AH=CH=100米,
∴AB=100-100≈73(m),
∵60千米/小时=m/s,
∴=14.6(m/s)<≈16.7(m/s),
∴此车没有超速.
23.【答案】解:
(1)在ABC中,ACB=,AB=10 cm,BC=6 cm,由勾股当t=时,PA=PB.
(2)当t=时,点P恰好在BAC的平分线上.
第2页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共10小题,共30分)
已知ABC的三边长分别为5,13,12,则ABC的面积为( )
A. B. C. D. 不能确定
由下列条件能判定ABC为直角三角形的是( )
A. B.
C. ,, D.
用反证法证明:a,b至少有一个为0,应该假设( )
A. ,都不为 B. ,只有一个为
C. ,至多一个为 D. ,都为
如图,点D在ABC的边AC上,将ABC沿BD翻折后,点A恰好与点C重合.若BC=5,CD=3,则BD的长为( )
A. B. C. D.
如图,两个较大正方形的面积分别为225,289,则字母A所代表的正方形的面积为( )
A. B. C. D.
如图,在44的方格纸中,有一个格点三角形ABC,关于它的描述正确的是( )
A. 三边长都是有理数 B. 是等腰三角形
C. 是直角三角形 D. 有一条边长为
将一根长度为16 cm自然伸直的弹性皮筋AB两端固定在水平的桌面上,然后把中点C竖直向上拉升6 cm至D点(如图),则该弹性皮筋被拉长了( )
A. B. C. D.
如图,在ABC中,B=,两直角边AB=7,BC=24,在三角形内有一点P到各边的距离相等,则这个距离是( )
A. B. C. D.
如图,在四边形ABCD中,ADBC,C=,BCD与BC'D关于直线BD对称,BC=6,CD=3,点C与点C'对应,BC'交AD于点E,则线段DE的长为( )
A. B. C. D.
图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=6,BC=5,将四个直角三角形中的边长为6的直角边分别向外延长一倍,得到图2所示的“数学风车”,则这个风车的外围周长是( )
A. B. C. D. 无法确定
二、填空题(本大题共5小题,共15分)
在ABC中,C=,若AB=5,则++= .
如图,O为数轴原点,A,B两点分别对应-3,3,作腰长为4的等腰ABC,连结OC,以O为圆心,OC长为半径画弧交数轴于点M,则点M对应的实数为 .
如图,分别以RtABC的三边为边长向外作等边三角形.若AB=2,则三个等边三角形的面积之和是 .
我国古代有这样一道数学问题:“枯木一根直立地上,高二丈,周三尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何 ”题意是:如图所示,把枯木看作一个圆柱体,因一丈是十尺,则该圆柱的高为20尺,底面周长为3尺,有葛藤自点A处缠绕而上,绕五周后其末端恰好到达点B处.求问题中葛藤的最短长度是 尺.
如图是某公园的平面示意图,公园的入口位于点O,由点O向北、向东分别为两条互相垂直的甬道.古塔位于点A处,从古塔出发沿射线OA方向前行300 m是盆景园B,从盆景园B向左转90°后直走400 m到达梅花阁C.若点A用有序数对(400,300)表示,则点C可表示为________.
三、解答题(本大题共8小题,共75分)
如图,在ABC中,AC=5,BC=12,AB=13,D是BC的中点,求AD的长和ABD的面积.
已知:A,B,C是ABC的内角.用反证法证明:A,B,C中至少有一个角大于或等于.
如图,AC=BC=BD=1,AD=,求ABD的面积.
已知a,b,c满足++|c-|=0.
(1)求a,b,c的值;
(2)试问以a,b,c为边能否构成直角三角形 请说明理由.
如图,AD是ABC中BC边上的高,P是AD上任意一点.当P从A向D移动时,线段PB,PC的长都在变化,试探索-的值如何变化
如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画图.
(1)画一个直角三角形,使它的面积为3;
(2)画一个正方形,使它的面积为10;
(3)画一个等腰直角三角形,使它的面积为8.
“为了安全,请勿超速”.如图,一条公路建成通车,在某直线路段MN上限速60千米/时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.
如图,在ABC中,ACB=,AB=10 cm,BC=6 cm.若点P从点A出发,以每秒1 cm的速度沿折线A-C-B-A运动,设运动时间为t s(t>0).
(1)若点P在AC上,且满足PA=PB时,求出此时t的值;
(2)若点P恰好在BAC的平分线上(但不与A点重合),求t的值.
参考答案
1.【答案】A
2.【答案】A
3.【答案】A
4.【答案】D
5.【答案】D
6.【答案】D
7.【答案】B
8.【答案】B
9.【答案】B
10.【答案】C
11.【答案】50
12.【答案】
13.【答案】2
14.【答案】25
15.【答案】(400,800)
16.【答案】解:AD=,=15.
17.【答案】证明:假设A,B,C都小于,
即A<,B<,C<,
则A+B+C<.
这与“三角形的内角和等于”矛盾,
所以假设不成立.
因此,A,B,C中至少有一个角大于或等于.
18.【答案】解:=ABBD=.
19.【答案】解:(1)++|c-|=0,
a-=0,b-3=0,c-=0.
a=,b=3,c=.
(2)能构成直角三角形.
理由:
∵b2=9=a2+c2,
∴以a,b,c为边的三角形是直角三角形.
20.【答案】解:-的值不变.
理由:ADBC,ADB=ADC=.
根据勾股定理,得=+,=+.
-=+-(+)=-.
-的值不变,
-的值不变.
21.【答案】解:(1)如图.
(2)如图.
(3)如图.
22.【答案】解:此车没有超速.
理由:过C作CH⊥MN于H,
∵∠CBN=60°,BC=200米,
∴∠HCB=30°,
∴BH===100(米),
,
即(米),
∵∠CAN=45°,
∴AH=CH=100米,
∴AB=100-100≈73(m),
∵60千米/小时=m/s,
∴=14.6(m/s)<≈16.7(m/s),
∴此车没有超速.
23.【答案】解:
(1)在ABC中,ACB=,AB=10 cm,BC=6 cm,由勾股当t=时,PA=PB.
(2)当t=时,点P恰好在BAC的平分线上.
第2页,共2页
