黑龙江省哈尔滨市五常市部分学校2021-2022学年九年级上学期期中联考数学试题(图片版含答案)
文档属性
| 名称 | 黑龙江省哈尔滨市五常市部分学校2021-2022学年九年级上学期期中联考数学试题(图片版含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-27 00:00:00 | ||
图片预览




文档简介
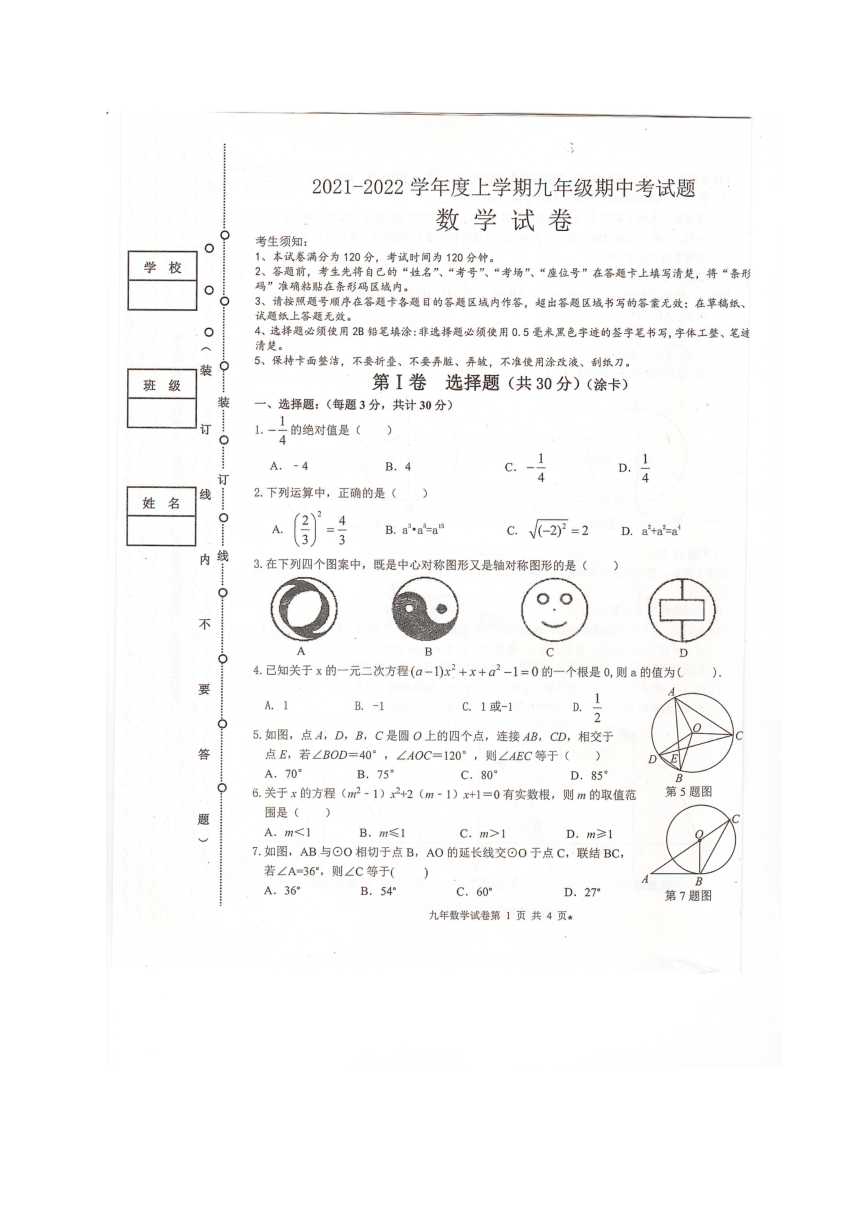
2021-2022学年度上学期九年级期中考试题
数学试卷参考答案
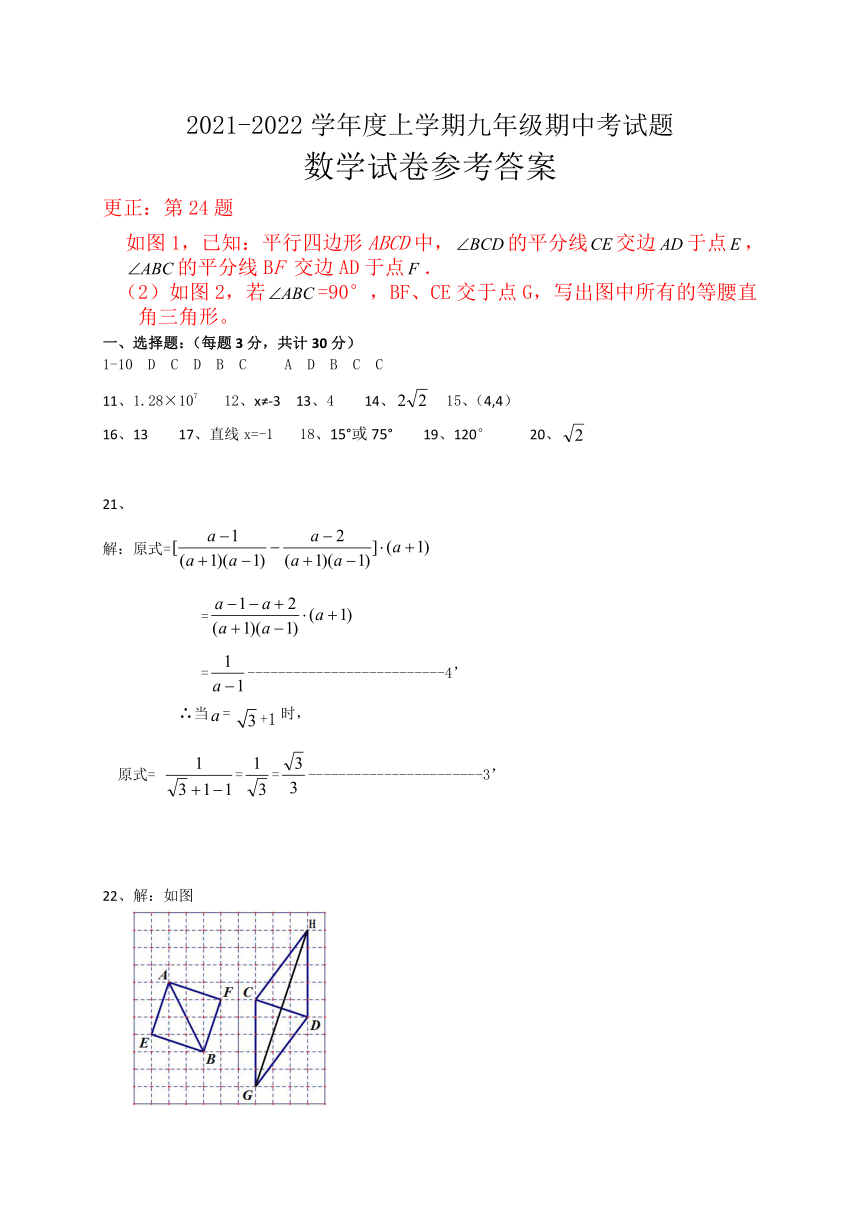
更正:第24题
如图1,已知:平行四边形ABCD中,的平分线交边于点,的平分线BF 交边AD于点.
(2)如图2,若=90°,BF、CE交于点G,写出图中所有的等腰直角三角形。
一、选择题:(每题3分,共计30分)
1-10 D C D B C A D B C C
11、1.28×107 12、x≠-3 13、4 14、 15、(4,4)
16、13 17、直线x=-1 18、15°或75° 19、120° 20、
21、
解:原式=
=
=--------------------------4’
∴当= +1时,
原式= ==-----------------------3’
22、解:如图
GH= --------7’
23、
解:(1)(名) 答:一共调查了100名学生. -------------------2’
(2)100-30-20-10=40(名)
补图略
答:出扇形统计图中阅读部分的扇形圆心角的度数是108°.. ------------------4’
(3) (名)
答:估计参加阅读和其它活动的学生一共有600名.--------------------2’
24、(1)证明:∵ 四边形是平行四边形,
,
,
又∵ BG平分,平分
,
,.
,(
,即. ---------------------4’
(2)△ABF,△CDE,△BCG,△EFG----------------------------4’
25、(1)解:设A款羽绒服每件网上的售价元,B款羽绒服每件网上的售价b元,得
….3分 解….2分
答:A款400元,B款300元. --------------------------5’
(2)设该商户让利的羽绒服有件,则已售出的有(20-)件,得
600 (20-x) + 600×60% x -400×10 -300×10≥3800 ……3分
解得….2分
答: 该商户让利销售的羽绒服最多是5件.----------------------------------5’
26、(1)证明:连接BD
∵AB为圆O的直径,
∴∠ADB=90°,即BD⊥AC,
∴AD=DC=BD=AC。-------------------------2’
(2)证明:连接BD,
在Rt△ABC中,∠ABC=90°,AB=BC,
∴∠A=∠C=45°,
由(1)可知
∴AD=DC=BD=AC,∠CBD=∠C=45°,
∴∠A=∠FBD,
∵DF⊥DG,
∴∠FDG=90°,
∴∠FDB+∠BDG=90°,
∵∠EDA+∠BDG=90°,
∴∠EDA=∠FDB,
在△AED和△BFD中,
,
∴△AED≌△BFD(ASA),
∴AE=BF;-------------------------4’
(3)解:连接EF
∵△AED≌△BFD,
∴DE=DF,
∵∠EDF=90°,
∴△EDF是等腰直角三角形,
∵AE=BF,AE=1,
∴BF=1,
∵CF=2
∴AB=BC=3
∴BE=2
在Rt△EBF中,∠EBF=90°,
根据勾股定理得:EF2=EB2+BF2,
∴EF==,
∵△DEF为等腰直角三角形,∠EDF=90°,
∴由勾股定理得EF=ED,
∵EF=,
∴DE=×=,-------------------------4’
27、
(1)∵抛物线y=ax2+bx+c经过A(-3,0)、B(1,0)、C(0,3)三点
∴
解得
∴解析式为y=-x2-2x+3----------------------------2’
(2)∵-x2-2x+3=-(x+1)2+4,
∴抛物线顶点坐标D为(-1,4).
∵A(-3,0),D(-1,4),
∴设AD为解析式为y=kx+b,有,
解得,
∴AD解析式:y=2x+6,
∵P在AD上,
∴P(x,2x+6),
∴S△APE=PEyP=(-x)(2x+6)=-x2-3x,
∴S=-x2-3x----------------------------3’
(3)∵S=-x2-3x=
∴当x=-时,S取最大值.
∴P(-,3)
∵△PEF沿EF翻折得△P′EF,且P(-,3),
∴∠PFE=∠P′FE,PF=P′F=3,PE=P′E=,
∵PF∥y轴,
∴∠PFE=∠FEN,
∵∠PFE=∠P′FE,
∴∠FEN=∠P′FE,
∴EN=FN
设EN=m,则FN=m,P′N=3-m,
在Rt△P′EN中,
∵
∴m=
如图1,设P′F与y轴交于点N,过P′作P′M⊥y轴于点M,
∵S△P′EN= P′N·P′E=EN·P′M
∴P′M=.
在Rt△EMP′中,
∵EM=,
∴OM=EO-EM=,
∴P′(,).----------------------------5’
数学试卷参考答案
更正:第24题
如图1,已知:平行四边形ABCD中,的平分线交边于点,的平分线BF 交边AD于点.
(2)如图2,若=90°,BF、CE交于点G,写出图中所有的等腰直角三角形。
一、选择题:(每题3分,共计30分)
1-10 D C D B C A D B C C
11、1.28×107 12、x≠-3 13、4 14、 15、(4,4)
16、13 17、直线x=-1 18、15°或75° 19、120° 20、
21、
解:原式=
=
=--------------------------4’
∴当= +1时,
原式= ==-----------------------3’
22、解:如图
GH= --------7’
23、
解:(1)(名) 答:一共调查了100名学生. -------------------2’
(2)100-30-20-10=40(名)
补图略
答:出扇形统计图中阅读部分的扇形圆心角的度数是108°.. ------------------4’
(3) (名)
答:估计参加阅读和其它活动的学生一共有600名.--------------------2’
24、(1)证明:∵ 四边形是平行四边形,
,
,
又∵ BG平分,平分
,
,.
,(
,即. ---------------------4’
(2)△ABF,△CDE,△BCG,△EFG----------------------------4’
25、(1)解:设A款羽绒服每件网上的售价元,B款羽绒服每件网上的售价b元,得
….3分 解….2分
答:A款400元,B款300元. --------------------------5’
(2)设该商户让利的羽绒服有件,则已售出的有(20-)件,得
600 (20-x) + 600×60% x -400×10 -300×10≥3800 ……3分
解得….2分
答: 该商户让利销售的羽绒服最多是5件.----------------------------------5’
26、(1)证明:连接BD
∵AB为圆O的直径,
∴∠ADB=90°,即BD⊥AC,
∴AD=DC=BD=AC。-------------------------2’
(2)证明:连接BD,
在Rt△ABC中,∠ABC=90°,AB=BC,
∴∠A=∠C=45°,
由(1)可知
∴AD=DC=BD=AC,∠CBD=∠C=45°,
∴∠A=∠FBD,
∵DF⊥DG,
∴∠FDG=90°,
∴∠FDB+∠BDG=90°,
∵∠EDA+∠BDG=90°,
∴∠EDA=∠FDB,
在△AED和△BFD中,
,
∴△AED≌△BFD(ASA),
∴AE=BF;-------------------------4’
(3)解:连接EF
∵△AED≌△BFD,
∴DE=DF,
∵∠EDF=90°,
∴△EDF是等腰直角三角形,
∵AE=BF,AE=1,
∴BF=1,
∵CF=2
∴AB=BC=3
∴BE=2
在Rt△EBF中,∠EBF=90°,
根据勾股定理得:EF2=EB2+BF2,
∴EF==,
∵△DEF为等腰直角三角形,∠EDF=90°,
∴由勾股定理得EF=ED,
∵EF=,
∴DE=×=,-------------------------4’
27、
(1)∵抛物线y=ax2+bx+c经过A(-3,0)、B(1,0)、C(0,3)三点
∴
解得
∴解析式为y=-x2-2x+3----------------------------2’
(2)∵-x2-2x+3=-(x+1)2+4,
∴抛物线顶点坐标D为(-1,4).
∵A(-3,0),D(-1,4),
∴设AD为解析式为y=kx+b,有,
解得,
∴AD解析式:y=2x+6,
∵P在AD上,
∴P(x,2x+6),
∴S△APE=PEyP=(-x)(2x+6)=-x2-3x,
∴S=-x2-3x----------------------------3’
(3)∵S=-x2-3x=
∴当x=-时,S取最大值.
∴P(-,3)
∵△PEF沿EF翻折得△P′EF,且P(-,3),
∴∠PFE=∠P′FE,PF=P′F=3,PE=P′E=,
∵PF∥y轴,
∴∠PFE=∠FEN,
∵∠PFE=∠P′FE,
∴∠FEN=∠P′FE,
∴EN=FN
设EN=m,则FN=m,P′N=3-m,
在Rt△P′EN中,
∵
∴m=
如图1,设P′F与y轴交于点N,过P′作P′M⊥y轴于点M,
∵S△P′EN= P′N·P′E=EN·P′M
∴P′M=.
在Rt△EMP′中,
∵EM=,
∴OM=EO-EM=,
∴P′(,).----------------------------5’
同课章节目录
