2.2 振动的描述课件(56张PPT)
文档属性
| 名称 | 2.2 振动的描述课件(56张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 915.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-11-26 00:00:00 | ||
图片预览











文档简介
(共56张PPT)
第2节 振动的描述
一、振动特征的描述
1.振幅:
(1)定义:振动物体离开平衡位置的_________,用符号__表示。
(2)物理意义:表示振动的_____,是_____(选填“标量”或“矢量”)。
最大距离
强弱
标量
A
2.周期和频率:
(1)全振动:振动物体从某一初始状态开始经过一定时间之后第一次又回到_____
状态的过程。
(2)周期:振动物体完成___________所经历的时间。
(3)频率:在一段时间内,物体完成全振动的次数与这段时间_____。
(4)固有周期(或固有频率):物体在_________下的振动周期(或频率),它只由振
动系统___________决定。
(5)物理意义:周期和频率都是表示振动物体振动_____的物理量,周期越小,频率
越大,振动得_____。周期和频率的关系是T=
原来
一次全振动
之比
自然状态
本身的性质
越快
快慢
二、简谐运动的位移图像
【思考】
简谐运动的位移图像可以直接读出哪些物理量
提示:由图像可以直接读取振幅A和周期T,可以求出频率f。
1.图像特点:简谐运动的图像是一条_____________曲线,如图所示。
正弦(或余弦)
2.图像的意义:表示做简谐运动的物体在任意时刻相对于平衡位置的_____。即
表示做简谐运动的物体偏离平衡位置的_____随时间的变化关系。
3.图像信息:从图像上可知_____和_____,还可知道任一时刻_____的大小和方向。
位移
位移
振幅
周期
位移
三、简谐运动的位移公式
1.表达式:
x=Asinωt= 或x=Asin(ωt+φ0)。
2.公式中各符号的含义:
3.圆频率ω与周期(或频率)的关系:
ω= =_____。
2πf
关键能力·素养形成
一 描述简谐运动的物理量的分析
1.全振动:
(1)振动特征:一个完整的振动过程。
(2)物理量特征:位移(x)、加速度(a)、速度(v)等各物理量第一次同时与初始状态相同。
(3)时间特征:历时一个周期。
(4)路程特征:振幅的4倍。
(5)相位特征:增加2π。
2.振动中几个常见量与振幅的关系:
(1)路程与振幅的关系:
①一个周期内的路程为振幅的4倍;
②半个周期内的路程为振幅的2倍。
(2)周期(或频率)与振幅的关系:
在简谐运动中,一个确定的振动系统的周期(或频率)是固定的,与振幅无关。
(3)振动系统的能量和振幅的关系:
对于一个确定的振动系统来说,系统的能量仅由振幅决定,振幅越大,振动系统的能量就越大。
【思考·讨论】
两个相同的水平方向放置的弹簧振子,一个拉伸至距平衡位置l0处释放,另一个拉伸至距平衡位置2l0处释放。它们的初相位、圆频率、振幅是否相同 (物理观念)
提示:它们都是从最大位移处释放,初相位相同;它们的固有频率与振幅大小无关,圆频率相同;它们离开平衡位置的最大位移不同,所以振幅不同。
【典例示范】
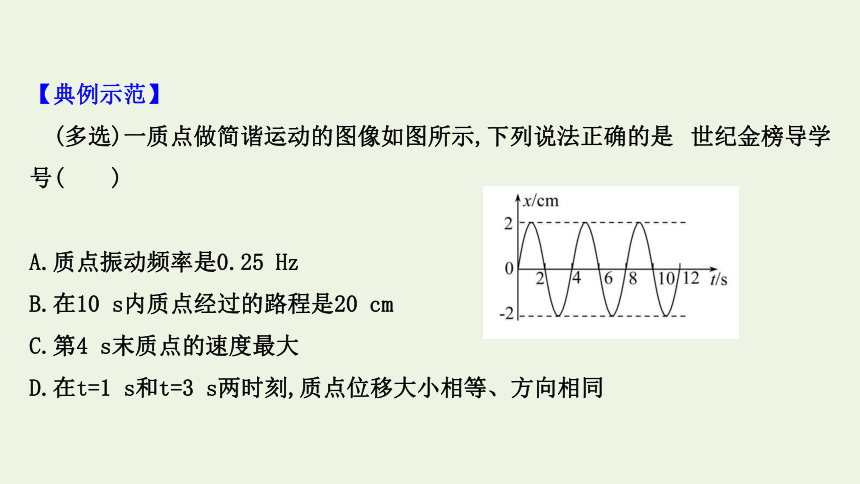
(多选)一质点做简谐运动的图像如图所示,下列说法正确的是 世纪金榜导学号( )
A.质点振动频率是0.25 Hz
B.在10 s内质点经过的路程是20 cm
C.第4 s末质点的速度最大
D.在t=1 s和t=3 s两时刻,质点位移大小相等、方向相同
【解题探究】
(1)如何求简谐运动的频率
提示:f= 。
(2)振动物体完成一次全振动通过的路程与振幅有什么关系
提示:振动物体完成一次全振动通过的路程为振幅的4倍。
【解析】选A、B、C。振动图像表示质点在不同时刻相对平衡位置的位移,由图像
可知,质点运动的周期T=4 s,其频率f= =0.25 Hz,故A正确;10 s内质点运动
了 T,其运动路程为s= ×4A= ×4×2 cm=20 cm,故B正确;第4 s末质点在
平衡位置,其速度最大,故C正确;t=1 s和t=3 s两时刻,由图像可知,位移大小相
等、方向相反,故D错误。
【规律方法】求解简谐运动路程的方法技巧
(1)振动物体在一个周期内的路程一定为4倍振幅,则在n个周期内的路程为n·4A。
(2)振动物体在半个周期内的路程一定为2倍振幅。
(3)振动物体在 内的路程可能等于一个振幅,可能小于一个振幅,也可能大于一个
振幅。只有当 的初始时刻振动物体在平衡位置或最大位移处时, 内的路程才
等于一个振幅。
【素养训练】
1.如图所示,弹簧振子在M、N之间做周期为T,振幅为A的简谐运动。O为平衡位
置,P是ON间的一点。若振子向右通过P点时开始计时,则经过 T,则振子通过的
路程 ( )
A.一定大于A B.一定小于A
C.一定等于A D.可能小于A
【解析】选B。振子向右通过P点时开始计时,速度逐渐减小,则经过 的平均速
度小于一个周期内的平均速度,则经过 振子通过的路程一定小于A,故选B。
2.(多选)如图所示是一做简谐运动的物体的振动图像,下列说法正确的是 ( )
A.振动周期是4×10-2 s
B.0~2×10-2 s内物体的位移是0 cm
C.物体的振动频率为4 Hz
D.物体的振幅是20 cm
【解析】选A、B。根据图像可知完成一个完整振动的时间即振动周期为4×
10-2 s,故A正确;0时刻和第2×10-2 s末物体都在平衡位置,所以0~2×10-2 s内
物体的位移是0 cm,故B正确;物体的频率:f= =25 Hz,故C错误;根据图像可知
振幅为10 cm,故D错误;所以选A、B。
3.如图所示,将弹簧振子从平衡位置拉下一段距离Δx,释放后振子在A、B间振动,且AB=20 cm,振子由A到B的时间为0.1 s,则下列说法中正确的是 ( )
A.振子在A、B两点时,弹簧弹力大小相等
B.振子由A到O的时间比振子由O到B的时间短
C.振子完成一次全振动通过的路程为20 cm
D.若使振子在AB=10 cm间振动,则振子由A到B
的时间仍为0.1 s
【解析】选D。在A、B两点,弹力大小并不相等,但回复力相等,故A错误;据对称性,振子从A到O和从O到B时间相同,B错误;一次全振动的路程为4A=40 cm,C错误;由于周期不变,仍为0.2 s,A到B仍用时0.1 s,D正确。
【补偿训练】
有一个在光滑水平面内的弹簧振子,第一次用力把弹簧压缩x后释放让它振动,第二次把弹簧压缩2x后释放让它振动,则先后两次振动的周期之比和振幅之比分别为 ( )
A.1∶1,1∶1 B.1∶1,1∶2
C.1∶4,1∶4 D.1∶2,1∶2
【解析】选B。周期与振幅无关,两次振动周期相等。振幅等于最大位移的大小,两次的振幅之比为1∶2,选项B正确。
二 简谐运动图像的应用
1.图像的意义:图像反映了做简谐运动的质点位移随时间的变化规律,并不表示质点运动的轨迹。如弹簧振子运动的轨迹为直线,但其x-t图像是一条正弦(或余弦)曲线。
2.由图像可以得出的量:
简谐运动的图像如图所示,由此可以得出:
(1)由图像可以直接读取振幅A。
(2)由图像可以直接读取周期T,进而求出频率f。
(3)由图像可知质点在不同时刻的位移。
(4)x-t图像上某一点的斜率表示该时刻的速度,斜率的绝对值为速度的大小,斜率的正负为速度的方向。所以,图中t1时刻质点的速度比t2时刻质点的速度小,t1时刻速度方向为负,t2时刻速度方向也为负。
(5)从图像可以看出质点在不同时刻之间的相位差。
(6)由图像可以比较不同时刻质点加速度的大小和方向。例如,在上图中t1时刻振动的位移x1为正,则加速度a1为负,t2时刻x2为负,则加速度a2为正,又因为|x1|>|x2|,所以|a1|>|a2|。
3.周期性:做简谐运动的物体,每隔一段时间总重复前面的运动,也就是说其运动
具有周期性。不同的简谐运动,其周期一般是不同的。根据简谐运动的周期性可
作出判断:
(1)若t2-t1=nT,则t1、t2两时刻振动物体在同一位置,运动情况相同。
(2)若t2-t1=nT+ T,则t1、t2两时刻振动物体所处的位置关于平衡位置对称,描
述运动的物理量(x、F、a)大小相等,方向相反。
(3)若t2-t1=nT+ T或t2-t1=nT+ T,则当t1时刻物体到达最大位移处时,t2时刻物
体到达平衡位置;当t1时刻物体在平衡位置时,t2时刻物体到达最大位移处;若t1
时刻物体在其他位置,t2时刻物体到达何处就要视具体情况而定。
【思考·讨论】
如图,在小塑料瓶底部穿一小孔,并装满墨水悬挂在支架上,使其在支架所在竖直平面内摆动,操作者沿v方向水平匀速拉动白纸,分析在白纸上留下的图像。
(1)白纸上留下的图像是不是振动物体运动的轨迹 (物理观念)
(2)由图像可以得到描述振动的哪个物理量 (物理观念)
提示:(1)振动物体在竖直平面内来回摆动,所以图像不是振动物体运动的轨迹,但反映了振动物体相对于平衡位置的位移随时间变化的规律。
(2)由图像可测得振动物体偏离平衡位置的最大距离即振幅,可以计算物体完成一次振动的时间即周期。
【典例示范】
如图甲所示,弹簧振子以O点为平衡位置,在A、B两点之间做简谐运动,取向右为正方向,振子的位移x随时间t的变化如图乙所示,下列说法正确的是 世纪金榜导学号( )
A.从t=0到t=1.6 s过程中,振子通过的路程为48 cm
B.t=0.2 s时,振子在O点右侧6 cm处
C.t=0.4 s和t=1.2 s时,振子的加速度相同
D.t=0.4 s到t=0.8 s的时间内,振子的速度逐渐减小
【解析】选A。从t=0到t=1.6 s,恰好是一个周期,所以振子通过的路程为4个振幅,即4×12 cm=48 cm,故A正确;在0~0.4 s内,振子做减速运动,不是匀速运动,所以t=0.2 s时,振子不在O点右侧6 cm处,故B错误;在t=0.4 s和t=1.2 s时,振子分别位于B点和A点,根据牛顿第二定律可知,振子的加速度大小相同,方向相反,故C错误;t=0.4 s到t=0.8 s的时间内,振子的位移减小,正向平衡位置运动,振子的速度逐渐增大,故D错误。
【规律方法】简谐运动图像的应用技巧
(1)判断质点任意时刻的位移大小和方向:质点任意时刻的位移大小看质点离开平衡位置距离的大小即可,也可比较图像中纵坐标值的大小。方向由坐标值的正负判断或质点相对平衡位置的方向判断。
(2)判断质点任意时刻的加速度(回复力)大小和方向:由于加速度(回复力)的大小与位移大小成正比,方向与位移方向相反,所以只要从图像中得出质点在任意时刻的位移大小和方向即可。
(3)判断质点任意时刻的速度大小和方向:x-t图像上该时刻图线的斜率表示此时的速度。斜率的绝对值为速度的大小,斜率的正负为速度的方向。
【素养训练】
1.如图所示为某弹簧振子在0到5 s内的振动图像,由图可知,下列说法中正确的是 ( )
A.振动周期为5 s,振幅为8 cm
B.第2 s末振子的速度为零,加速度为负向的最大值
C.第3 s内振子的加速度逐渐增大
D.从第3 s末到第4 s末振子做减速运动
【解析】选D。根据图像可知,振动周期为4 s,振幅为8 cm,A错误;第2秒末,振子到达波谷处,速度为零,加速度最大,回复力指向正向,所以加速度为正向最大,B错误;第3秒内,即2到3这一秒,振子在向平衡位置移动,回复力减小,加速度减小,C错误;从第 3 s 末到第 4 s 末振子从平衡位置向波峰移动,速度越来越小,D正确。所以选D。
2.一质点做简谐运动时,其振动图像如图所示。由图可知,在t1和t2时刻,质点运动的 ( )
A.位移相同 B.回复力相同
C.速度相同 D.加速度相同
【解析】选C。从题图中可以看出,在t1和t2时刻,质点的位移大小相等、方向相反。由公式F=-kx可知,在t1和t2时刻质点所受的回复力大小相等、方向相反,加速度大小相等、方向相反,A、B、D错误;在t1和t2时刻,质点速度方向相同,由于位移大小相等,所以速度大小相等,C正确。
3.如图甲所示,金属小球用轻弹簧连接在固定的光滑斜面顶端。小球在斜面上做简谐运动,到达最高点时,弹簧处于原长。取沿斜面向上为正方向,小球的振动图像如图乙所示。则 ( )
A.弹簧的最大伸长量为4 cm
B.t=0.2 s时,弹簧的弹性势能最大
C.t=0.2 s到t=0.6 s内,小球的重力势能逐渐减小
D.t=0到t=0.2 s内,振子的速度增大
【解析】选C。小球的振幅等于振子位移的最大值,由图读出,振幅为A=2 cm,由于当振子到达最高点时,弹簧处于原长,所以弹簧的最大伸长量为2A=4 cm,故选项A错误;由图可知t=0.2 s时,弹簧处于原长,弹簧的弹性势能最小,为零,故选项B错误;t=0.2 s到t=0.6 s内,小球沿斜面向下运动,小球的重力势能逐渐减小,故选项C正确;t=0时小球经过平衡位置沿斜面向上运动,0.2 s时到达最高点,在这个过程中速度减小,故选项D错误。所以选C。
三 简谐运动表达式的含义
1.简谐运动的表达式:x=Asin(ωt+φ0)。
2.ω与φ0的物理意义:
(1)ω:圆频率,表示简谐运动质点振动的快慢。与周期T及频率f的关系:ω=
=2πf。
(2)φ0:表示t=0时,简谐运动质点所处的状态,称为初相位或初相。ωt+φ0代表
做简谐运动的质点在t时刻处在一个运动周期中的状态,称为简谐运动的相位。
3.从运动方程中得到的物理量:根据运动方程x=Asin(ωt+φ0),结合ω= =
2πf,可确定简谐运动的振幅为A、周期为 、频率为 、初相位为φ0。
【特别提醒】
(1)写振动方程首先要确定三个量,振幅A、圆频率ω= 和初相位φ0。
(2)由于振动具有周期性,振动问题往往具有多解性,解决有关振动问题时,要注
意多解问题,避免漏解。
【思考·讨论】
我们借用匀速圆周运动来推导简谐运动的公式:如图小球P在绕O点以角速度ω做圆周运动,小球在x轴上的投影的运动等效为振动,以小球P在顶点的时刻作为计时零点,A为小球到圆心的竖直距离。
(1)小球在x轴上投影的最大距离可等效为描述振
动的哪个物理量,大小是多少 (物理观念)
(2)经过时间t小球投影的位移大小是多少 (科学思维)
提示:(1)振动的振幅,大小为A。
(2)经过时间t小球转过的角度为ωt,所以投影的位移为x=Asinωt。
【典例示范】
某质点做简谐运动,其位移随时间变化的关系式为x=5sin t(cm) ,则下列
关于质点运动的说法中正确的是 ( )
世纪金榜导学号
A.1 s时和3 s时速度相同①
B.3 s时和5 s时位移相同
C.在 t=4 s时质点的加速度最大②
D.在 t=4 s时质点的速度最大③
【审题关键】
序号 信息提取
① 速度是矢量,包含大小和方向
② 位移最大时,加速度最大
③ 在平衡位置时,速度最大
【解析】选D。由公式x=5sin t可知,1 s时和3 s时的位移相同,根据对称性可
知,两时刻质点的振动速度大小相等,方向相反,故A错误;由公式x=5sin t可知,
x3=5sin π,x5=5sin π,故两时刻质点的位移不同,故B错误;在t=4 s时质点的
位移x=5sin t=0,说明物体通过平衡位置,速度最大,加速度为0,故C错误,D正确。
【规律方法】利用表达式x=Asin(ωt+φ0)解题的方法技巧
(1)首先明确表达式中各物理量的意义:
①A表示简谐运动的振幅。
②ω表示做简谐运动的圆频率。
③ωt+φ0表示简谐运动的相位,φ0表示初相位。
(2)根据公式ω= =2πf可确定三个描述振动快慢的物理量。
(3)根据表达式可求解某时刻的位移。
(4)对于同一质点的振动,不同形式的位移表达式初相位不同。
【素养训练】
1.(多选)有两个简谐运动,其表达式分别是x1=4sin(100πt+ )cm,x2=5sin(100πt
+ )cm,下列说法正确的是 ( )
A.它们的振幅相同
B.它们的周期相同
C.它们的相位差恒定
D.它们的振动步调一致
【解析】选B、C。它们的振幅分别是4 cm、5 cm,故不同,选项A不符合题意;ω都是
100π rad/s,所以周期(T= )都是 s,选项B符合题意;由Δφ=(100πt+ )-
(100πt+ )= 得相位差恒定,选项C符合题意;Δφ≠0,即振动步调不一致,选项D
不符合题意。
2.物体A做简谐运动的振动位移为xA=3cos(100t+ ) m,物体B做简谐运动的振
动位移为xB=5cos(100t+ ) m。比较A、B的运动可知( )
A.振幅是矢量,A的振幅是6 m,B的振幅是10 m
B.周期是标量,A、B的周期相等,均为100 s
C.A振动的频率fA等于B振动的频率fB
D.A振动的频率fA大于B振动的频率fB
【解析】选C。振幅是标量,A、B的振动范围分别是6 m、10 m,但振幅分别是
3 m、5 m,选项A错误;周期是标量,A、B的周期T= s=6.28×10-2 s,选项
B错误;因为TA=TB,故fA=fB,选项C正确,选项D错误。
3.如图所示,一弹簧振子在M、N间沿光滑水平杆做简谐运动,坐标原点O为平衡位
置,MN=4 cm。从小球在图中N点时开始计时,到第一次经过O点的时间为0.1 s,则
小球振动的周期为________ s,振动方程的表达式为x=________ cm。
【解析】如题图,从正向最大位移处开始计时,振动方程的表达式为:x=A cosωt;
其中振幅 A=2 cm;据题可得:T=4×0.1 s=0.4 s,则ω= =5π rad/s则振动方程
的表达式为:x=2cos5πt cm。
答案:0.4 2cos5πt
【补偿训练】
两个简谐运动的表达式分别为x1=4sin4πt(cm)和x2=2sin2πt(cm),它们的振幅之比、各自的频率之比是( )
A.2∶1,2∶1 B.1∶2,1∶2
C.2∶1,1∶2 D.1∶2,2∶1
【解析】选A。由题意知A1=4 cm,A2=2 cm,ω1=4π rad/s,ω2=2π rad/s,则A1∶A2=2∶1,f1∶f2=ω1∶ω2=2∶1。故A正确,B、C、D错误。
【拓展例题】考查内容:简谐运动的周期性和对称性
【典例】一弹簧振子做简谐运动,周期为T,则正确的说法是 ( )
A.若t时刻和(t+Δt)时刻振子运动位移大小相等、方向相同,则Δt一定等于T的
整数倍
B.若t时刻和(t+Δt)时刻振子运动速度大小相等、方向相同,则Δt一定等于 的
整数倍
C.若Δt=T,则在t时刻和(t+Δt)时刻振子运动的加速度一定相等
D.若Δt= ,则在t时刻和(t+Δt)时刻弹簧的长度一定相等
【解析】选C。做简谐运动时,振子由平衡位置到最大位移,再由最大位移回到平衡位置,两次经过同一点时,它们的位移大小相等、方向相同,其时间间隔并不等于周期的整数倍,所以A选项错误。当振子沿同一方向经过关于平衡位置对称的两位置时,其速度的大小、方向均一样,所以B选项错误。根据简谐运动的对称性知,C选项正确。当振子先后出现在两个端点时,恰相隔半个周期,而弹簧的长度不等,所以D选项错误。
【课堂回眸】
课堂检测·素养达标
1.(多选)一质点做简谐运动的图像如图所示,下列说法正确的是 ( )
A.t=1 s时质点的速度最小
B.t=2 s时质点所受的回复力最大
C.质点振动的振幅为4 cm
D.质点振动的频率为4 Hz
【解析】选A、C。在t=1 s时质点位于负的最大位移处,速度为0,加速度最大,A
正确;t=2 s时位移为0,故质点所受的回复力为0,B错误;由图可知质点振动的振
幅为4 cm,周期为T=4 s,则频率为f= =0.25 Hz,C正确,D错误。
2.如图1所示,弹簧振子在竖直方向做简谐运动。以其平衡位置为坐标原点,竖直向上为正方向建立坐标轴,振子的位移x随时间t的变化如图2所示,下列说法正确的是 ( )
A.振子的振幅为4 cm
B.振子的振动周期为1 s
C.t=1 s时,振子的速度为正的最大值
D.t=1 s时,振子的加速度为正的最大值
【解析】选C。由振动图像可知,该弹簧振子的振幅为2 cm,周期为2 s,t=1 s时,振子在平衡位置,速度为正的最大值,加速度为零,故C正确。
3.某质点做简谐运动,其位移随时间变化的关系式为x=5sin t cm,则以下关于
该质点的说法不正确的是 ( )
A.该质点振动的振幅是5 cm
B.该质点振动的频率为8 Hz
C.第1 s末与第3 s末的位移相同
D.3 s末至5 s末的速度方向都相同
【解析】选B。把简谐运动的公式x=Asinωt与该质点的位移表达式x=5sin t cm
相对比可知,该质点振动的振幅是5 cm,A正确;由位移表达式可知该质点振动的圆
频率ω= ,所以频率为f= Hz,B错误;由位移表达式x=5sin t cm可知,第
1 s末位移为 cm,第3 s末的位移也为 cm,C正确;周期为8 s,故3 s末至
5 s末( T)的速度方向一直为负方向,D正确。故选B。
4.一质点做简谐运动,其位移和时间关系如图所示。 世纪金榜导学号
(1)求t=0.25×10-2 s时的位移。
(2)在t=1.5×10-2 s到2×10-2 s的振动过程中,质点的位移、回复力、速度、动能、势能如何变化
(3)在t=0到8.5×10-2 s时间内,质点的路程、位移各多大
【解析】(1)由题图可知,A=2 cm,T=2×10-2 s,
振动方程为x=Asin(ωt- )=-Acos ωt
=-2cos t cm=-2cos(102πt) cm
当t=0.25×10-2 s时,x=-2cos cm=- cm。
(2)由题图可知在1.5×10-2~2×10-2 s内,质点的位移变大,回复力变大,速度变
小,动能变小,势能变大。
(3)从t=0至8.5×10-2 s的时间内,
质点的路程为s=17A=34 cm,位移为2 cm。
答案:(1)- cm (2)变大 变大 变小 变小 变大
(3)34 cm 2 cm
第2节 振动的描述
一、振动特征的描述
1.振幅:
(1)定义:振动物体离开平衡位置的_________,用符号__表示。
(2)物理意义:表示振动的_____,是_____(选填“标量”或“矢量”)。
最大距离
强弱
标量
A
2.周期和频率:
(1)全振动:振动物体从某一初始状态开始经过一定时间之后第一次又回到_____
状态的过程。
(2)周期:振动物体完成___________所经历的时间。
(3)频率:在一段时间内,物体完成全振动的次数与这段时间_____。
(4)固有周期(或固有频率):物体在_________下的振动周期(或频率),它只由振
动系统___________决定。
(5)物理意义:周期和频率都是表示振动物体振动_____的物理量,周期越小,频率
越大,振动得_____。周期和频率的关系是T=
原来
一次全振动
之比
自然状态
本身的性质
越快
快慢
二、简谐运动的位移图像
【思考】
简谐运动的位移图像可以直接读出哪些物理量
提示:由图像可以直接读取振幅A和周期T,可以求出频率f。
1.图像特点:简谐运动的图像是一条_____________曲线,如图所示。
正弦(或余弦)
2.图像的意义:表示做简谐运动的物体在任意时刻相对于平衡位置的_____。即
表示做简谐运动的物体偏离平衡位置的_____随时间的变化关系。
3.图像信息:从图像上可知_____和_____,还可知道任一时刻_____的大小和方向。
位移
位移
振幅
周期
位移
三、简谐运动的位移公式
1.表达式:
x=Asinωt= 或x=Asin(ωt+φ0)。
2.公式中各符号的含义:
3.圆频率ω与周期(或频率)的关系:
ω= =_____。
2πf
关键能力·素养形成
一 描述简谐运动的物理量的分析
1.全振动:
(1)振动特征:一个完整的振动过程。
(2)物理量特征:位移(x)、加速度(a)、速度(v)等各物理量第一次同时与初始状态相同。
(3)时间特征:历时一个周期。
(4)路程特征:振幅的4倍。
(5)相位特征:增加2π。
2.振动中几个常见量与振幅的关系:
(1)路程与振幅的关系:
①一个周期内的路程为振幅的4倍;
②半个周期内的路程为振幅的2倍。
(2)周期(或频率)与振幅的关系:
在简谐运动中,一个确定的振动系统的周期(或频率)是固定的,与振幅无关。
(3)振动系统的能量和振幅的关系:
对于一个确定的振动系统来说,系统的能量仅由振幅决定,振幅越大,振动系统的能量就越大。
【思考·讨论】
两个相同的水平方向放置的弹簧振子,一个拉伸至距平衡位置l0处释放,另一个拉伸至距平衡位置2l0处释放。它们的初相位、圆频率、振幅是否相同 (物理观念)
提示:它们都是从最大位移处释放,初相位相同;它们的固有频率与振幅大小无关,圆频率相同;它们离开平衡位置的最大位移不同,所以振幅不同。
【典例示范】
(多选)一质点做简谐运动的图像如图所示,下列说法正确的是 世纪金榜导学号( )
A.质点振动频率是0.25 Hz
B.在10 s内质点经过的路程是20 cm
C.第4 s末质点的速度最大
D.在t=1 s和t=3 s两时刻,质点位移大小相等、方向相同
【解题探究】
(1)如何求简谐运动的频率
提示:f= 。
(2)振动物体完成一次全振动通过的路程与振幅有什么关系
提示:振动物体完成一次全振动通过的路程为振幅的4倍。
【解析】选A、B、C。振动图像表示质点在不同时刻相对平衡位置的位移,由图像
可知,质点运动的周期T=4 s,其频率f= =0.25 Hz,故A正确;10 s内质点运动
了 T,其运动路程为s= ×4A= ×4×2 cm=20 cm,故B正确;第4 s末质点在
平衡位置,其速度最大,故C正确;t=1 s和t=3 s两时刻,由图像可知,位移大小相
等、方向相反,故D错误。
【规律方法】求解简谐运动路程的方法技巧
(1)振动物体在一个周期内的路程一定为4倍振幅,则在n个周期内的路程为n·4A。
(2)振动物体在半个周期内的路程一定为2倍振幅。
(3)振动物体在 内的路程可能等于一个振幅,可能小于一个振幅,也可能大于一个
振幅。只有当 的初始时刻振动物体在平衡位置或最大位移处时, 内的路程才
等于一个振幅。
【素养训练】
1.如图所示,弹簧振子在M、N之间做周期为T,振幅为A的简谐运动。O为平衡位
置,P是ON间的一点。若振子向右通过P点时开始计时,则经过 T,则振子通过的
路程 ( )
A.一定大于A B.一定小于A
C.一定等于A D.可能小于A
【解析】选B。振子向右通过P点时开始计时,速度逐渐减小,则经过 的平均速
度小于一个周期内的平均速度,则经过 振子通过的路程一定小于A,故选B。
2.(多选)如图所示是一做简谐运动的物体的振动图像,下列说法正确的是 ( )
A.振动周期是4×10-2 s
B.0~2×10-2 s内物体的位移是0 cm
C.物体的振动频率为4 Hz
D.物体的振幅是20 cm
【解析】选A、B。根据图像可知完成一个完整振动的时间即振动周期为4×
10-2 s,故A正确;0时刻和第2×10-2 s末物体都在平衡位置,所以0~2×10-2 s内
物体的位移是0 cm,故B正确;物体的频率:f= =25 Hz,故C错误;根据图像可知
振幅为10 cm,故D错误;所以选A、B。
3.如图所示,将弹簧振子从平衡位置拉下一段距离Δx,释放后振子在A、B间振动,且AB=20 cm,振子由A到B的时间为0.1 s,则下列说法中正确的是 ( )
A.振子在A、B两点时,弹簧弹力大小相等
B.振子由A到O的时间比振子由O到B的时间短
C.振子完成一次全振动通过的路程为20 cm
D.若使振子在AB=10 cm间振动,则振子由A到B
的时间仍为0.1 s
【解析】选D。在A、B两点,弹力大小并不相等,但回复力相等,故A错误;据对称性,振子从A到O和从O到B时间相同,B错误;一次全振动的路程为4A=40 cm,C错误;由于周期不变,仍为0.2 s,A到B仍用时0.1 s,D正确。
【补偿训练】
有一个在光滑水平面内的弹簧振子,第一次用力把弹簧压缩x后释放让它振动,第二次把弹簧压缩2x后释放让它振动,则先后两次振动的周期之比和振幅之比分别为 ( )
A.1∶1,1∶1 B.1∶1,1∶2
C.1∶4,1∶4 D.1∶2,1∶2
【解析】选B。周期与振幅无关,两次振动周期相等。振幅等于最大位移的大小,两次的振幅之比为1∶2,选项B正确。
二 简谐运动图像的应用
1.图像的意义:图像反映了做简谐运动的质点位移随时间的变化规律,并不表示质点运动的轨迹。如弹簧振子运动的轨迹为直线,但其x-t图像是一条正弦(或余弦)曲线。
2.由图像可以得出的量:
简谐运动的图像如图所示,由此可以得出:
(1)由图像可以直接读取振幅A。
(2)由图像可以直接读取周期T,进而求出频率f。
(3)由图像可知质点在不同时刻的位移。
(4)x-t图像上某一点的斜率表示该时刻的速度,斜率的绝对值为速度的大小,斜率的正负为速度的方向。所以,图中t1时刻质点的速度比t2时刻质点的速度小,t1时刻速度方向为负,t2时刻速度方向也为负。
(5)从图像可以看出质点在不同时刻之间的相位差。
(6)由图像可以比较不同时刻质点加速度的大小和方向。例如,在上图中t1时刻振动的位移x1为正,则加速度a1为负,t2时刻x2为负,则加速度a2为正,又因为|x1|>|x2|,所以|a1|>|a2|。
3.周期性:做简谐运动的物体,每隔一段时间总重复前面的运动,也就是说其运动
具有周期性。不同的简谐运动,其周期一般是不同的。根据简谐运动的周期性可
作出判断:
(1)若t2-t1=nT,则t1、t2两时刻振动物体在同一位置,运动情况相同。
(2)若t2-t1=nT+ T,则t1、t2两时刻振动物体所处的位置关于平衡位置对称,描
述运动的物理量(x、F、a)大小相等,方向相反。
(3)若t2-t1=nT+ T或t2-t1=nT+ T,则当t1时刻物体到达最大位移处时,t2时刻物
体到达平衡位置;当t1时刻物体在平衡位置时,t2时刻物体到达最大位移处;若t1
时刻物体在其他位置,t2时刻物体到达何处就要视具体情况而定。
【思考·讨论】
如图,在小塑料瓶底部穿一小孔,并装满墨水悬挂在支架上,使其在支架所在竖直平面内摆动,操作者沿v方向水平匀速拉动白纸,分析在白纸上留下的图像。
(1)白纸上留下的图像是不是振动物体运动的轨迹 (物理观念)
(2)由图像可以得到描述振动的哪个物理量 (物理观念)
提示:(1)振动物体在竖直平面内来回摆动,所以图像不是振动物体运动的轨迹,但反映了振动物体相对于平衡位置的位移随时间变化的规律。
(2)由图像可测得振动物体偏离平衡位置的最大距离即振幅,可以计算物体完成一次振动的时间即周期。
【典例示范】
如图甲所示,弹簧振子以O点为平衡位置,在A、B两点之间做简谐运动,取向右为正方向,振子的位移x随时间t的变化如图乙所示,下列说法正确的是 世纪金榜导学号( )
A.从t=0到t=1.6 s过程中,振子通过的路程为48 cm
B.t=0.2 s时,振子在O点右侧6 cm处
C.t=0.4 s和t=1.2 s时,振子的加速度相同
D.t=0.4 s到t=0.8 s的时间内,振子的速度逐渐减小
【解析】选A。从t=0到t=1.6 s,恰好是一个周期,所以振子通过的路程为4个振幅,即4×12 cm=48 cm,故A正确;在0~0.4 s内,振子做减速运动,不是匀速运动,所以t=0.2 s时,振子不在O点右侧6 cm处,故B错误;在t=0.4 s和t=1.2 s时,振子分别位于B点和A点,根据牛顿第二定律可知,振子的加速度大小相同,方向相反,故C错误;t=0.4 s到t=0.8 s的时间内,振子的位移减小,正向平衡位置运动,振子的速度逐渐增大,故D错误。
【规律方法】简谐运动图像的应用技巧
(1)判断质点任意时刻的位移大小和方向:质点任意时刻的位移大小看质点离开平衡位置距离的大小即可,也可比较图像中纵坐标值的大小。方向由坐标值的正负判断或质点相对平衡位置的方向判断。
(2)判断质点任意时刻的加速度(回复力)大小和方向:由于加速度(回复力)的大小与位移大小成正比,方向与位移方向相反,所以只要从图像中得出质点在任意时刻的位移大小和方向即可。
(3)判断质点任意时刻的速度大小和方向:x-t图像上该时刻图线的斜率表示此时的速度。斜率的绝对值为速度的大小,斜率的正负为速度的方向。
【素养训练】
1.如图所示为某弹簧振子在0到5 s内的振动图像,由图可知,下列说法中正确的是 ( )
A.振动周期为5 s,振幅为8 cm
B.第2 s末振子的速度为零,加速度为负向的最大值
C.第3 s内振子的加速度逐渐增大
D.从第3 s末到第4 s末振子做减速运动
【解析】选D。根据图像可知,振动周期为4 s,振幅为8 cm,A错误;第2秒末,振子到达波谷处,速度为零,加速度最大,回复力指向正向,所以加速度为正向最大,B错误;第3秒内,即2到3这一秒,振子在向平衡位置移动,回复力减小,加速度减小,C错误;从第 3 s 末到第 4 s 末振子从平衡位置向波峰移动,速度越来越小,D正确。所以选D。
2.一质点做简谐运动时,其振动图像如图所示。由图可知,在t1和t2时刻,质点运动的 ( )
A.位移相同 B.回复力相同
C.速度相同 D.加速度相同
【解析】选C。从题图中可以看出,在t1和t2时刻,质点的位移大小相等、方向相反。由公式F=-kx可知,在t1和t2时刻质点所受的回复力大小相等、方向相反,加速度大小相等、方向相反,A、B、D错误;在t1和t2时刻,质点速度方向相同,由于位移大小相等,所以速度大小相等,C正确。
3.如图甲所示,金属小球用轻弹簧连接在固定的光滑斜面顶端。小球在斜面上做简谐运动,到达最高点时,弹簧处于原长。取沿斜面向上为正方向,小球的振动图像如图乙所示。则 ( )
A.弹簧的最大伸长量为4 cm
B.t=0.2 s时,弹簧的弹性势能最大
C.t=0.2 s到t=0.6 s内,小球的重力势能逐渐减小
D.t=0到t=0.2 s内,振子的速度增大
【解析】选C。小球的振幅等于振子位移的最大值,由图读出,振幅为A=2 cm,由于当振子到达最高点时,弹簧处于原长,所以弹簧的最大伸长量为2A=4 cm,故选项A错误;由图可知t=0.2 s时,弹簧处于原长,弹簧的弹性势能最小,为零,故选项B错误;t=0.2 s到t=0.6 s内,小球沿斜面向下运动,小球的重力势能逐渐减小,故选项C正确;t=0时小球经过平衡位置沿斜面向上运动,0.2 s时到达最高点,在这个过程中速度减小,故选项D错误。所以选C。
三 简谐运动表达式的含义
1.简谐运动的表达式:x=Asin(ωt+φ0)。
2.ω与φ0的物理意义:
(1)ω:圆频率,表示简谐运动质点振动的快慢。与周期T及频率f的关系:ω=
=2πf。
(2)φ0:表示t=0时,简谐运动质点所处的状态,称为初相位或初相。ωt+φ0代表
做简谐运动的质点在t时刻处在一个运动周期中的状态,称为简谐运动的相位。
3.从运动方程中得到的物理量:根据运动方程x=Asin(ωt+φ0),结合ω= =
2πf,可确定简谐运动的振幅为A、周期为 、频率为 、初相位为φ0。
【特别提醒】
(1)写振动方程首先要确定三个量,振幅A、圆频率ω= 和初相位φ0。
(2)由于振动具有周期性,振动问题往往具有多解性,解决有关振动问题时,要注
意多解问题,避免漏解。
【思考·讨论】
我们借用匀速圆周运动来推导简谐运动的公式:如图小球P在绕O点以角速度ω做圆周运动,小球在x轴上的投影的运动等效为振动,以小球P在顶点的时刻作为计时零点,A为小球到圆心的竖直距离。
(1)小球在x轴上投影的最大距离可等效为描述振
动的哪个物理量,大小是多少 (物理观念)
(2)经过时间t小球投影的位移大小是多少 (科学思维)
提示:(1)振动的振幅,大小为A。
(2)经过时间t小球转过的角度为ωt,所以投影的位移为x=Asinωt。
【典例示范】
某质点做简谐运动,其位移随时间变化的关系式为x=5sin t(cm) ,则下列
关于质点运动的说法中正确的是 ( )
世纪金榜导学号
A.1 s时和3 s时速度相同①
B.3 s时和5 s时位移相同
C.在 t=4 s时质点的加速度最大②
D.在 t=4 s时质点的速度最大③
【审题关键】
序号 信息提取
① 速度是矢量,包含大小和方向
② 位移最大时,加速度最大
③ 在平衡位置时,速度最大
【解析】选D。由公式x=5sin t可知,1 s时和3 s时的位移相同,根据对称性可
知,两时刻质点的振动速度大小相等,方向相反,故A错误;由公式x=5sin t可知,
x3=5sin π,x5=5sin π,故两时刻质点的位移不同,故B错误;在t=4 s时质点的
位移x=5sin t=0,说明物体通过平衡位置,速度最大,加速度为0,故C错误,D正确。
【规律方法】利用表达式x=Asin(ωt+φ0)解题的方法技巧
(1)首先明确表达式中各物理量的意义:
①A表示简谐运动的振幅。
②ω表示做简谐运动的圆频率。
③ωt+φ0表示简谐运动的相位,φ0表示初相位。
(2)根据公式ω= =2πf可确定三个描述振动快慢的物理量。
(3)根据表达式可求解某时刻的位移。
(4)对于同一质点的振动,不同形式的位移表达式初相位不同。
【素养训练】
1.(多选)有两个简谐运动,其表达式分别是x1=4sin(100πt+ )cm,x2=5sin(100πt
+ )cm,下列说法正确的是 ( )
A.它们的振幅相同
B.它们的周期相同
C.它们的相位差恒定
D.它们的振动步调一致
【解析】选B、C。它们的振幅分别是4 cm、5 cm,故不同,选项A不符合题意;ω都是
100π rad/s,所以周期(T= )都是 s,选项B符合题意;由Δφ=(100πt+ )-
(100πt+ )= 得相位差恒定,选项C符合题意;Δφ≠0,即振动步调不一致,选项D
不符合题意。
2.物体A做简谐运动的振动位移为xA=3cos(100t+ ) m,物体B做简谐运动的振
动位移为xB=5cos(100t+ ) m。比较A、B的运动可知( )
A.振幅是矢量,A的振幅是6 m,B的振幅是10 m
B.周期是标量,A、B的周期相等,均为100 s
C.A振动的频率fA等于B振动的频率fB
D.A振动的频率fA大于B振动的频率fB
【解析】选C。振幅是标量,A、B的振动范围分别是6 m、10 m,但振幅分别是
3 m、5 m,选项A错误;周期是标量,A、B的周期T= s=6.28×10-2 s,选项
B错误;因为TA=TB,故fA=fB,选项C正确,选项D错误。
3.如图所示,一弹簧振子在M、N间沿光滑水平杆做简谐运动,坐标原点O为平衡位
置,MN=4 cm。从小球在图中N点时开始计时,到第一次经过O点的时间为0.1 s,则
小球振动的周期为________ s,振动方程的表达式为x=________ cm。
【解析】如题图,从正向最大位移处开始计时,振动方程的表达式为:x=A cosωt;
其中振幅 A=2 cm;据题可得:T=4×0.1 s=0.4 s,则ω= =5π rad/s则振动方程
的表达式为:x=2cos5πt cm。
答案:0.4 2cos5πt
【补偿训练】
两个简谐运动的表达式分别为x1=4sin4πt(cm)和x2=2sin2πt(cm),它们的振幅之比、各自的频率之比是( )
A.2∶1,2∶1 B.1∶2,1∶2
C.2∶1,1∶2 D.1∶2,2∶1
【解析】选A。由题意知A1=4 cm,A2=2 cm,ω1=4π rad/s,ω2=2π rad/s,则A1∶A2=2∶1,f1∶f2=ω1∶ω2=2∶1。故A正确,B、C、D错误。
【拓展例题】考查内容:简谐运动的周期性和对称性
【典例】一弹簧振子做简谐运动,周期为T,则正确的说法是 ( )
A.若t时刻和(t+Δt)时刻振子运动位移大小相等、方向相同,则Δt一定等于T的
整数倍
B.若t时刻和(t+Δt)时刻振子运动速度大小相等、方向相同,则Δt一定等于 的
整数倍
C.若Δt=T,则在t时刻和(t+Δt)时刻振子运动的加速度一定相等
D.若Δt= ,则在t时刻和(t+Δt)时刻弹簧的长度一定相等
【解析】选C。做简谐运动时,振子由平衡位置到最大位移,再由最大位移回到平衡位置,两次经过同一点时,它们的位移大小相等、方向相同,其时间间隔并不等于周期的整数倍,所以A选项错误。当振子沿同一方向经过关于平衡位置对称的两位置时,其速度的大小、方向均一样,所以B选项错误。根据简谐运动的对称性知,C选项正确。当振子先后出现在两个端点时,恰相隔半个周期,而弹簧的长度不等,所以D选项错误。
【课堂回眸】
课堂检测·素养达标
1.(多选)一质点做简谐运动的图像如图所示,下列说法正确的是 ( )
A.t=1 s时质点的速度最小
B.t=2 s时质点所受的回复力最大
C.质点振动的振幅为4 cm
D.质点振动的频率为4 Hz
【解析】选A、C。在t=1 s时质点位于负的最大位移处,速度为0,加速度最大,A
正确;t=2 s时位移为0,故质点所受的回复力为0,B错误;由图可知质点振动的振
幅为4 cm,周期为T=4 s,则频率为f= =0.25 Hz,C正确,D错误。
2.如图1所示,弹簧振子在竖直方向做简谐运动。以其平衡位置为坐标原点,竖直向上为正方向建立坐标轴,振子的位移x随时间t的变化如图2所示,下列说法正确的是 ( )
A.振子的振幅为4 cm
B.振子的振动周期为1 s
C.t=1 s时,振子的速度为正的最大值
D.t=1 s时,振子的加速度为正的最大值
【解析】选C。由振动图像可知,该弹簧振子的振幅为2 cm,周期为2 s,t=1 s时,振子在平衡位置,速度为正的最大值,加速度为零,故C正确。
3.某质点做简谐运动,其位移随时间变化的关系式为x=5sin t cm,则以下关于
该质点的说法不正确的是 ( )
A.该质点振动的振幅是5 cm
B.该质点振动的频率为8 Hz
C.第1 s末与第3 s末的位移相同
D.3 s末至5 s末的速度方向都相同
【解析】选B。把简谐运动的公式x=Asinωt与该质点的位移表达式x=5sin t cm
相对比可知,该质点振动的振幅是5 cm,A正确;由位移表达式可知该质点振动的圆
频率ω= ,所以频率为f= Hz,B错误;由位移表达式x=5sin t cm可知,第
1 s末位移为 cm,第3 s末的位移也为 cm,C正确;周期为8 s,故3 s末至
5 s末( T)的速度方向一直为负方向,D正确。故选B。
4.一质点做简谐运动,其位移和时间关系如图所示。 世纪金榜导学号
(1)求t=0.25×10-2 s时的位移。
(2)在t=1.5×10-2 s到2×10-2 s的振动过程中,质点的位移、回复力、速度、动能、势能如何变化
(3)在t=0到8.5×10-2 s时间内,质点的路程、位移各多大
【解析】(1)由题图可知,A=2 cm,T=2×10-2 s,
振动方程为x=Asin(ωt- )=-Acos ωt
=-2cos t cm=-2cos(102πt) cm
当t=0.25×10-2 s时,x=-2cos cm=- cm。
(2)由题图可知在1.5×10-2~2×10-2 s内,质点的位移变大,回复力变大,速度变
小,动能变小,势能变大。
(3)从t=0至8.5×10-2 s的时间内,
质点的路程为s=17A=34 cm,位移为2 cm。
答案:(1)- cm (2)变大 变大 变小 变小 变大
(3)34 cm 2 cm
同课章节目录
- 第1章 动量及其守恒定律
- 第1节 动量和动量定理
- 第2节 动量守恒定律及其应用
- 第3节 科学验证:动量守恒定律
- 第4节 弹性碰撞与非弹性碰撞
- 第2章 机械振动
- 第1节 简谐运动
- 第2节 振动的描述
- 第3节 单摆
- 第4节 科学测量:用单摆测量重力加速度
- 第5节 生活中的振动
- 第3章 机械波
- 第1节 波的形成和描述
- 第2节 波的反射和折射
- 第3节 波的干涉和衍射
- 第4节 多普勒效应及其应用
- 第4章 光的折射和全反射
- 第1节 光的折射
- 第2节 科学测量:玻璃的折射率
- 第3节 光的全反射
- 第4节 光导纤维及其应用
- 第5章 光的干涉、衍射和偏振
- 第1节 光的干涉
- 第2节 科学测量:用双缝干涉测光的波长
- 第3节 光的衍射
- 第4节 光的偏振
- 第5节 激光与全息照相
