2.5 生活中的振动课件(34张PPT)
文档属性
| 名称 | 2.5 生活中的振动课件(34张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 730.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-11-26 00:00:00 | ||
图片预览









文档简介
(共34张PPT)
第5节 生活中的振动
一、阻尼振动
1.定义:在实际振动过程中,由于存在_____,振动系统的_______不断减小,_____
不断减小的振动叫作阻尼振动。
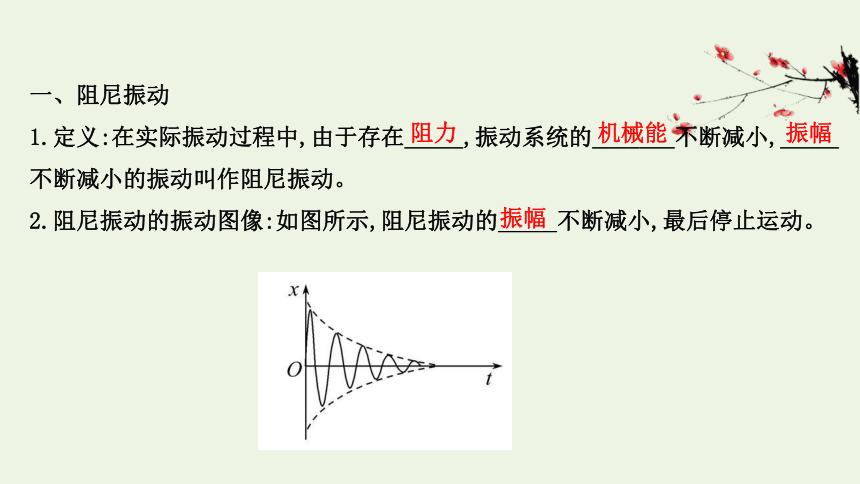
2.阻尼振动的振动图像:如图所示,阻尼振动的_____不断减小,最后停止运动。
阻力
机械能
振幅
振幅
3.阻尼振动的应用:如果想让物体尽快停止振动,就需要增大阻力。例如:
(1)汽车在凹凸不平的路面行驶时,会发生剧烈振动,通过_______增大阻力,可使
振动很快停止。
(2)仪表的指针在指示测量结果时常左右摆动,很难准确读数,设计时可让指针的
转动部分受到适当的阻力,使之迅速停下来,便于读数。
4.阻尼振动的防止:有时我们希望物体在某一段时间内的运动接近简谐运动,则
应减小阻力。例如,我们隔一段时间就要对摆钟进行清洗,并在轴承上加润滑油,
以减小阻力。
减震器
二、受迫振动与共振
1.驱动力:给振动物体施加的一个_______的外力。
2.受迫振动:在_______外力作用下产生的振动。
3.受迫振动的周期或频率:物体做受迫振动时,振动稳定后的周期(或频率)总等于
_______的周期或频率,与物体的固有周期(或固有频率)无关。
4.共振:
(1)条件:驱动力的周期(或频率)等于物体的_____________________。
(2)特征:共振时,物体振动的振幅最___(选填“大”或“小”)。
周期性
周期性
驱动力
固有周期(或固有频率)
大
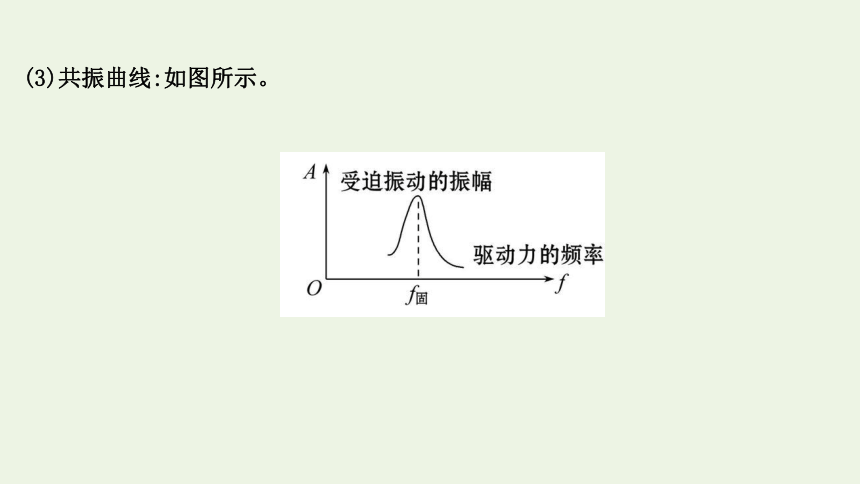
(3)共振曲线:如图所示。
三、共振的应用与防止
【思考】
修建桥梁时,需要将管柱打入河床中,工人常使打桩机打击管柱的频率接近管柱的固有频率,为什么
提示:让管柱接近共振状态而激烈振动,从而使管柱周围泥沙快速松动,提高打桩的效率。
1.共振的应用:
(1)共振破碎机:
①作用:用于旧水泥路面的破碎。
②原理:通过调节振动锤头的振动 _____,使其等于或接近水泥路面的固有频率,
使锤头下的水泥路面因局部共振而被击碎。
③特点:破碎效率高、破碎深度___。
频率
大
(2)音叉共鸣箱:
①共鸣的定义:把某一频率的音叉插在一端开口的共鸣箱上,当敲击音叉使它振
动时,箱内的空气柱就能产生共振,发出较响的声音,这种现象称为_____。
②共鸣的实质:共鸣是一种_______现象。
共鸣
声共振
2.共振的防止:
(1)轮船航行时,人们常通过改变轮船的航向和速率,使海浪冲击力的频率与轮船
的_________相差很大,以此防止共振现象。
(2)集体列队经过桥梁时要便步走,以防对桥梁形成周期性驱动力使桥梁发生共
振。
(3)许多机电设备,如车床、磨床、电锯等,工作时都会伴随不同程度的振动,要
防止它们产生共振现象。
(4)人体各个部位的_________不同,接近振动源时,应该设法防止共振对身体造
成的不良影响。
固有频率
固有频率
关键能力·素养形成
一 阻尼振动与简谐运动的比较
阻尼振动与简谐运动的比较:
振动类型
比较项目 阻尼振动 简谐运动
产生原因 受到阻力作用 不受阻力作用
振 幅 如果没有能量补充,物体的振幅会越来越小 振幅不变
振动能量 有损失 保持不变
振动频率 不变 不变
振动图像
实 例 汽车上的减震器的振动 弹簧振子在光滑面上的运动
【思考·讨论】
“余音绕梁,三日不绝”形容歌声或音乐的优美,耐人寻味。但在日常生活中,当弹奏结束后,乐声会越来越弱并最终消失,这是为什么呢 (物理观念)
提示:乐声受到空气的阻尼作用,振幅越来越小,因此乐声也就越来越弱了。
【典例示范】
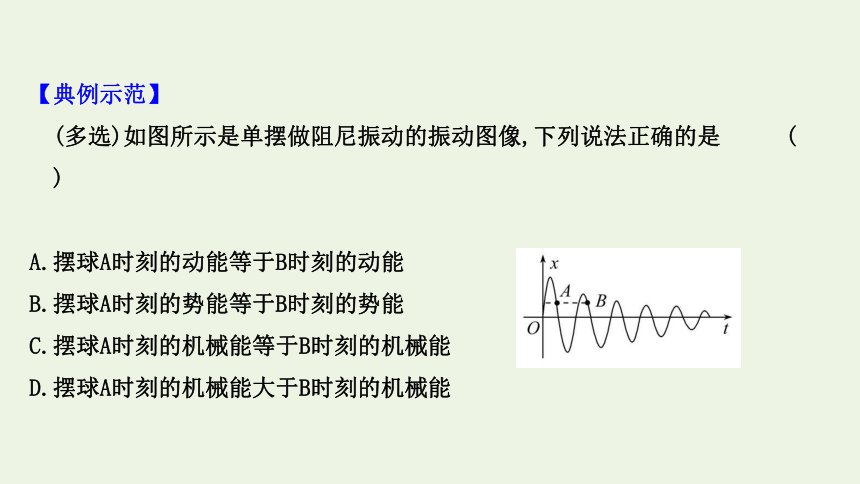
(多选)如图所示是单摆做阻尼振动的振动图像,下列说法正确的是 ( )
A.摆球A时刻的动能等于B时刻的动能
B.摆球A时刻的势能等于B时刻的势能
C.摆球A时刻的机械能等于B时刻的机械能
D.摆球A时刻的机械能大于B时刻的机械能
【解析】选B、D。因为单摆做阻尼振动,要不断克服阻力做功,振幅逐渐减小,机械能逐渐转化为其他形式的能,机械能不断减小,由于A、B两时刻单摆的位移相同,位置一样,所以势能相等,因为机械能减小,所以动能减小,B、D正确。
【素养训练】
1.单摆在空气中做阻尼振动,下列说法中正确的是 ( )
A.位移逐渐减小
B.速度逐渐减小
C.动能逐渐减小
D.振动的能量逐渐转化为其他形式的能
【解析】选D。单摆在空气中做阻尼振动时,由于克服阻力做功,所以振动能量会逐渐减少,并转化为其他形式的能,选项D对;但是其位移、速度以及动能都会交替变化,所以选项A、B、C错。
2.弹簧振子在空气中做阻尼振动,下列说法中正确的是 ( )
A.振子位移逐渐减小
B.振动周期逐渐减小
C.振子动能逐渐减小
D.振动系统的能量逐渐减小
【解析】选D。振子在空气中做阻尼振动时,振幅减小,周期不变,总能量减小,A、B、C错误,D正确。
【补偿训练】
弹簧振子可以做简谐运动,考虑阻力存在,振子振动过程中能量不断损失,这种振
动称为阻尼振动。现通过实验手段得到某振子阻尼振动的图像和经理论推导得到
阻尼振动的周期公式T= (ω0为该振子无阻尼时的角速度,β为阻尼系数、
对某次阻尼振动β为常数),审题后指出阻尼振动的特点___________、
_________________________(写出两点)。
【解析】从图中可以看出阻尼振动的振幅在减小,
但是振动周期不变。
答案:振幅逐渐减小 周期不变
二 自由振动、受迫振动和共振的比较
自由振动、受迫振动、共振的比较:
振动类型
比较项目 自由振动 受迫振动 共 振
振动原因 受回复力作用 受周期性驱动力作用 受周期性驱动力作用
振动周期
或频率 由系统本身性质决定,即固有周期或固有频率 由驱动力的周期或频率决定,即T=T驱或f=f驱 T驱=T固
或f驱=f固
振动能量 振动系统的机械能不变 由产生驱动力的物体提供 振动物体获得的能量最大
常见例子 弹簧振子
或单摆 扬声器纸盆的振动 共振筛、声音的共鸣
【特别提醒】(1)振幅的大小表征一个振动系统总机械能的大小,当振动过程有介质阻力做功时,机械能转化为内能,机械能减少,振幅减小。
(2)物体做受迫振动时,驱动力的频率与物体的固有频率相差越小,受迫振动振幅越大,驱动力的频率等于物体的固有频率时振幅最大。
【思考·讨论】
用扁担挑水时,有时桶里的水会荡得厉害,并从桶中溅出来,这是为什么 (物理观念)
提示:人挑水时,通过扁担对水桶施加周期性的驱动力,当驱动力的频率等于桶里水的固有频率时,水发生共振,水的动荡就越来越厉害,就会从桶中溅出来。
【典例示范】
为了交通安全,常在公路上设置如图所示的减速带,减速带使路面稍微拱起以达到车辆减速的目的。一排等间距设置的减速带,可有效降低车速,称为洗衣板效应。如果某路面上的减速带的间距为1.5 m,一辆固有频率为2 Hz的汽车匀速驶过这排减速带,下列说法正确的是 ( )
A.当汽车以5 m/s的速度行驶时,其振动频率为2 Hz
B.当汽车以3 m/s的速度行驶时最不颠簸
C.当汽车以3 m/s的速度行驶时颠簸得最厉害
D.汽车速度越大,颠簸得就越厉害
【解析】选C。当汽车以5 m/s的速度行驶时,驱动力的周期为T= s=0.3 s,
所以频率f= Hz ,故A错;当汽车以3 m/s的速度行驶时,汽车的频率为f′
= Hz=2 Hz,此时和固有频率相同,所以振动最厉害,故C正确,B错误;当固有
频率等于驱动力的频率时,发生共振,振动的振幅最大,则越颠簸,和速度无关,故
D错;故选C。
【素养训练】
1.下列说法错误的是 ( )
A.某物体做自由振动时,其振动频率与振幅无关
B.某物体做受迫振动时,其振动频率与固有频率无关
C.某物体发生共振时的频率等于其固有频率
D.某物体发生共振时的振动就是无阻尼振动
【解析】选D。某物体做自由振动时,其振动频率与振幅无关,选项A正确;某物体做受迫振动时,其振动频率等于驱动力的频率,与固有频率无关,选项B正确;某物体发生共振时的频率等于其固有频率,选项C正确;某物体发生共振时的振动可能是阻尼振动,也可能是无阻尼振动,选项D错误;此题选择错误的选项,故选D。
2.如图所示,在一根张紧的绳子上挂几个摆,其中A、B的摆长相等。先让A摆振动起来,B、C、D三个摆随后也跟着振动起来,则稳定时 ( )
A.三个摆振动的振幅大小相等
B.三个摆的振幅大小不同,B摆的振幅最大
C.B摆的振动周期最大,D摆的振动周期最小
D.D摆的振动周期最大,C摆的振动周期最小
【解析】选B。由A摆摆动从而带动其他三个单摆做受迫振动,受迫振动中,当固有频率等于驱动力频率时,出现共振现象,振幅达到最大,由于B摆的固有频率与A摆的相同,故B摆发生共振,振幅最大,故A错误,B正确;受迫振动的频率等于驱动力的频率,故其他各摆振动周期跟A摆相同,C、D错误。
【拓展例题】考查内容:共振
【典例】(多选)铺设钢轨时,每两根钢轨接缝处都必须留有一定的间隙,匀速运动的列车经过轨端接缝处时,车轮就会受到一次冲击。由于每一根钢轨长度相等,所以这个冲击力是周期性的,列车由于受到周期性的冲击力做受迫振动。普通钢轨长为12.6 m,列车的固有振动周期为0.315 s。下列说法正确的是 ( )
A.列车的危险速率为40 m/s
B.列车过桥需要减速,是为了防止列车与桥发生共振现象
C.列车运行的振动频率和列车的固有频率总是相等的
D.增加钢轨的长度有利于列车高速运行
【解析】选A、B、D。对于受迫振动,当驱动力的频率与固有频率相等时发生共
振现象,所以列车的危险速率v= =40 m/s,A正确;为了防止共振现象发生,过桥
时需要减速,B正确;列车运行时的振动频率总等于驱动力的频率,只有共振时才
等于列车的固有频率,C错误;由v= 可知,L增大,T不变,v变大,所以D正确。
【课堂回眸】
课堂检测·素养达标
1.下列说法中正确的是 ( )
A.阻尼振动一定是减幅振动
B.物体做阻尼振动时,随着振幅的减小,频率也不断减小
C.受迫振动稳定时的频率等于驱动力的频率,与物体的固有频率无关
D.受迫振动的频率由驱动力和物体结构特点共同决定
【解析】选C。物体做阻尼振动时,如果有恰当的能量补充,也可以保持振幅不变,做等幅振动,所以阻尼振动的振幅是不一定改变的,所以A错误。物体做阻尼振动时,振幅虽然不断减小,但是振动的频率仍由自身的结构特点所决定,不随振幅的减小而变化,所以B错误。受迫振动稳定时的频率,只是取决于驱动力的频率,与物体自身结构特点无关,即与物体的固有频率无关,所以D错误,C正确。
2.下列关于机械振动的说法正确的是 ( )
A.受迫振动稳定后,其振动的周期总等于系统的固有周期
B.阻尼振动振幅逐渐减小时,周期也逐渐减小
C.当驱动力的频率等于振动系统的固有频率时,受迫振动的振幅最大
D.为避免共振现象发生,应使驱动力频率接近或等于振动系统的固有频率
【解析】选C。受迫振动稳定后,其振动的周期总等于驱动力的周期,选项A错误;阻尼振动振幅逐渐减小时,周期不变,选项B错误;当驱动力的频率等于振动系统的固有频率时,产生共振,此时受迫振动的振幅最大,选项C正确;为避免共振现象发生,应使驱动力频率远离振动系统的固有频率,故选项D错误。
3.如图甲所示,竖直圆盘转动时,可带动固定在圆盘上的T形支架在竖直方向振动,T形支架的下面系着一个弹簧和小球,共同组成一个振动系统。当圆盘静止时,小球可稳定振动。现使圆盘以4 s的周期匀速转动,经过一段时间后,小球振动达到稳定。改变圆盘匀速转动的周期,其共振曲线(振幅A与驱动力的频率f的关系)如图乙所示,则 ( )
A.此振动系统的固有频率约为0.25 Hz
B.此振动系统的固有频率约为3 Hz
C.若圆盘匀速转动的周期增大,系统振动的频率不变
D.若圆盘匀速转动的周期增大,共振曲线的峰值将向右移动
【解析】选B。由振子的共振曲线可得,此振动系统的固有频率约为3 Hz,故B正确,A错误;振动系统的振动频率是由驱动力的频率决定的,所以若圆盘匀速转动的周期增大,系统的振动频率减小,故C错误;共振曲线的峰值表示振子的固有频率,它是由振动系统本身的性质决定的,与驱动力的频率无关,故D错误。
4.如图甲所示,在一条张紧的绳子上挂几个摆,当a摆振动的时候,通过张紧的绳子给其他各摆施加驱动力,使其余各摆也振动起来,达到稳定时b摆和c摆的周期大小关系是:Tb________Tc,两个摆中________摆的振幅大,图乙是c摆稳定以后的振动图像,重力加速度为g,不计空气阻力,则a摆的摆长为________。
【解析】a摆摆动起来后,通过水平绳子对b、c两个摆施加周期性的驱动力,使b、
c两摆做受迫振动,两摆做受迫振动的频率等于驱动力的频率,由于驱动力频率相
同,则两摆的周期相同;受迫振动中,当固有频率等于驱动力频率时,出现共振现
象,振幅达到最大,由于c摆的固有频率与a摆的相同,故c摆发生共振,振幅最大;
a摆的固有周期与c摆的相同,由图乙可知,振动周期为:T=t0,由单摆周期公式T=
2π 即t0=2π ,知摆长为:L= 。
答案:= c
第5节 生活中的振动
一、阻尼振动
1.定义:在实际振动过程中,由于存在_____,振动系统的_______不断减小,_____
不断减小的振动叫作阻尼振动。
2.阻尼振动的振动图像:如图所示,阻尼振动的_____不断减小,最后停止运动。
阻力
机械能
振幅
振幅
3.阻尼振动的应用:如果想让物体尽快停止振动,就需要增大阻力。例如:
(1)汽车在凹凸不平的路面行驶时,会发生剧烈振动,通过_______增大阻力,可使
振动很快停止。
(2)仪表的指针在指示测量结果时常左右摆动,很难准确读数,设计时可让指针的
转动部分受到适当的阻力,使之迅速停下来,便于读数。
4.阻尼振动的防止:有时我们希望物体在某一段时间内的运动接近简谐运动,则
应减小阻力。例如,我们隔一段时间就要对摆钟进行清洗,并在轴承上加润滑油,
以减小阻力。
减震器
二、受迫振动与共振
1.驱动力:给振动物体施加的一个_______的外力。
2.受迫振动:在_______外力作用下产生的振动。
3.受迫振动的周期或频率:物体做受迫振动时,振动稳定后的周期(或频率)总等于
_______的周期或频率,与物体的固有周期(或固有频率)无关。
4.共振:
(1)条件:驱动力的周期(或频率)等于物体的_____________________。
(2)特征:共振时,物体振动的振幅最___(选填“大”或“小”)。
周期性
周期性
驱动力
固有周期(或固有频率)
大
(3)共振曲线:如图所示。
三、共振的应用与防止
【思考】
修建桥梁时,需要将管柱打入河床中,工人常使打桩机打击管柱的频率接近管柱的固有频率,为什么
提示:让管柱接近共振状态而激烈振动,从而使管柱周围泥沙快速松动,提高打桩的效率。
1.共振的应用:
(1)共振破碎机:
①作用:用于旧水泥路面的破碎。
②原理:通过调节振动锤头的振动 _____,使其等于或接近水泥路面的固有频率,
使锤头下的水泥路面因局部共振而被击碎。
③特点:破碎效率高、破碎深度___。
频率
大
(2)音叉共鸣箱:
①共鸣的定义:把某一频率的音叉插在一端开口的共鸣箱上,当敲击音叉使它振
动时,箱内的空气柱就能产生共振,发出较响的声音,这种现象称为_____。
②共鸣的实质:共鸣是一种_______现象。
共鸣
声共振
2.共振的防止:
(1)轮船航行时,人们常通过改变轮船的航向和速率,使海浪冲击力的频率与轮船
的_________相差很大,以此防止共振现象。
(2)集体列队经过桥梁时要便步走,以防对桥梁形成周期性驱动力使桥梁发生共
振。
(3)许多机电设备,如车床、磨床、电锯等,工作时都会伴随不同程度的振动,要
防止它们产生共振现象。
(4)人体各个部位的_________不同,接近振动源时,应该设法防止共振对身体造
成的不良影响。
固有频率
固有频率
关键能力·素养形成
一 阻尼振动与简谐运动的比较
阻尼振动与简谐运动的比较:
振动类型
比较项目 阻尼振动 简谐运动
产生原因 受到阻力作用 不受阻力作用
振 幅 如果没有能量补充,物体的振幅会越来越小 振幅不变
振动能量 有损失 保持不变
振动频率 不变 不变
振动图像
实 例 汽车上的减震器的振动 弹簧振子在光滑面上的运动
【思考·讨论】
“余音绕梁,三日不绝”形容歌声或音乐的优美,耐人寻味。但在日常生活中,当弹奏结束后,乐声会越来越弱并最终消失,这是为什么呢 (物理观念)
提示:乐声受到空气的阻尼作用,振幅越来越小,因此乐声也就越来越弱了。
【典例示范】
(多选)如图所示是单摆做阻尼振动的振动图像,下列说法正确的是 ( )
A.摆球A时刻的动能等于B时刻的动能
B.摆球A时刻的势能等于B时刻的势能
C.摆球A时刻的机械能等于B时刻的机械能
D.摆球A时刻的机械能大于B时刻的机械能
【解析】选B、D。因为单摆做阻尼振动,要不断克服阻力做功,振幅逐渐减小,机械能逐渐转化为其他形式的能,机械能不断减小,由于A、B两时刻单摆的位移相同,位置一样,所以势能相等,因为机械能减小,所以动能减小,B、D正确。
【素养训练】
1.单摆在空气中做阻尼振动,下列说法中正确的是 ( )
A.位移逐渐减小
B.速度逐渐减小
C.动能逐渐减小
D.振动的能量逐渐转化为其他形式的能
【解析】选D。单摆在空气中做阻尼振动时,由于克服阻力做功,所以振动能量会逐渐减少,并转化为其他形式的能,选项D对;但是其位移、速度以及动能都会交替变化,所以选项A、B、C错。
2.弹簧振子在空气中做阻尼振动,下列说法中正确的是 ( )
A.振子位移逐渐减小
B.振动周期逐渐减小
C.振子动能逐渐减小
D.振动系统的能量逐渐减小
【解析】选D。振子在空气中做阻尼振动时,振幅减小,周期不变,总能量减小,A、B、C错误,D正确。
【补偿训练】
弹簧振子可以做简谐运动,考虑阻力存在,振子振动过程中能量不断损失,这种振
动称为阻尼振动。现通过实验手段得到某振子阻尼振动的图像和经理论推导得到
阻尼振动的周期公式T= (ω0为该振子无阻尼时的角速度,β为阻尼系数、
对某次阻尼振动β为常数),审题后指出阻尼振动的特点___________、
_________________________(写出两点)。
【解析】从图中可以看出阻尼振动的振幅在减小,
但是振动周期不变。
答案:振幅逐渐减小 周期不变
二 自由振动、受迫振动和共振的比较
自由振动、受迫振动、共振的比较:
振动类型
比较项目 自由振动 受迫振动 共 振
振动原因 受回复力作用 受周期性驱动力作用 受周期性驱动力作用
振动周期
或频率 由系统本身性质决定,即固有周期或固有频率 由驱动力的周期或频率决定,即T=T驱或f=f驱 T驱=T固
或f驱=f固
振动能量 振动系统的机械能不变 由产生驱动力的物体提供 振动物体获得的能量最大
常见例子 弹簧振子
或单摆 扬声器纸盆的振动 共振筛、声音的共鸣
【特别提醒】(1)振幅的大小表征一个振动系统总机械能的大小,当振动过程有介质阻力做功时,机械能转化为内能,机械能减少,振幅减小。
(2)物体做受迫振动时,驱动力的频率与物体的固有频率相差越小,受迫振动振幅越大,驱动力的频率等于物体的固有频率时振幅最大。
【思考·讨论】
用扁担挑水时,有时桶里的水会荡得厉害,并从桶中溅出来,这是为什么 (物理观念)
提示:人挑水时,通过扁担对水桶施加周期性的驱动力,当驱动力的频率等于桶里水的固有频率时,水发生共振,水的动荡就越来越厉害,就会从桶中溅出来。
【典例示范】
为了交通安全,常在公路上设置如图所示的减速带,减速带使路面稍微拱起以达到车辆减速的目的。一排等间距设置的减速带,可有效降低车速,称为洗衣板效应。如果某路面上的减速带的间距为1.5 m,一辆固有频率为2 Hz的汽车匀速驶过这排减速带,下列说法正确的是 ( )
A.当汽车以5 m/s的速度行驶时,其振动频率为2 Hz
B.当汽车以3 m/s的速度行驶时最不颠簸
C.当汽车以3 m/s的速度行驶时颠簸得最厉害
D.汽车速度越大,颠簸得就越厉害
【解析】选C。当汽车以5 m/s的速度行驶时,驱动力的周期为T= s=0.3 s,
所以频率f= Hz ,故A错;当汽车以3 m/s的速度行驶时,汽车的频率为f′
= Hz=2 Hz,此时和固有频率相同,所以振动最厉害,故C正确,B错误;当固有
频率等于驱动力的频率时,发生共振,振动的振幅最大,则越颠簸,和速度无关,故
D错;故选C。
【素养训练】
1.下列说法错误的是 ( )
A.某物体做自由振动时,其振动频率与振幅无关
B.某物体做受迫振动时,其振动频率与固有频率无关
C.某物体发生共振时的频率等于其固有频率
D.某物体发生共振时的振动就是无阻尼振动
【解析】选D。某物体做自由振动时,其振动频率与振幅无关,选项A正确;某物体做受迫振动时,其振动频率等于驱动力的频率,与固有频率无关,选项B正确;某物体发生共振时的频率等于其固有频率,选项C正确;某物体发生共振时的振动可能是阻尼振动,也可能是无阻尼振动,选项D错误;此题选择错误的选项,故选D。
2.如图所示,在一根张紧的绳子上挂几个摆,其中A、B的摆长相等。先让A摆振动起来,B、C、D三个摆随后也跟着振动起来,则稳定时 ( )
A.三个摆振动的振幅大小相等
B.三个摆的振幅大小不同,B摆的振幅最大
C.B摆的振动周期最大,D摆的振动周期最小
D.D摆的振动周期最大,C摆的振动周期最小
【解析】选B。由A摆摆动从而带动其他三个单摆做受迫振动,受迫振动中,当固有频率等于驱动力频率时,出现共振现象,振幅达到最大,由于B摆的固有频率与A摆的相同,故B摆发生共振,振幅最大,故A错误,B正确;受迫振动的频率等于驱动力的频率,故其他各摆振动周期跟A摆相同,C、D错误。
【拓展例题】考查内容:共振
【典例】(多选)铺设钢轨时,每两根钢轨接缝处都必须留有一定的间隙,匀速运动的列车经过轨端接缝处时,车轮就会受到一次冲击。由于每一根钢轨长度相等,所以这个冲击力是周期性的,列车由于受到周期性的冲击力做受迫振动。普通钢轨长为12.6 m,列车的固有振动周期为0.315 s。下列说法正确的是 ( )
A.列车的危险速率为40 m/s
B.列车过桥需要减速,是为了防止列车与桥发生共振现象
C.列车运行的振动频率和列车的固有频率总是相等的
D.增加钢轨的长度有利于列车高速运行
【解析】选A、B、D。对于受迫振动,当驱动力的频率与固有频率相等时发生共
振现象,所以列车的危险速率v= =40 m/s,A正确;为了防止共振现象发生,过桥
时需要减速,B正确;列车运行时的振动频率总等于驱动力的频率,只有共振时才
等于列车的固有频率,C错误;由v= 可知,L增大,T不变,v变大,所以D正确。
【课堂回眸】
课堂检测·素养达标
1.下列说法中正确的是 ( )
A.阻尼振动一定是减幅振动
B.物体做阻尼振动时,随着振幅的减小,频率也不断减小
C.受迫振动稳定时的频率等于驱动力的频率,与物体的固有频率无关
D.受迫振动的频率由驱动力和物体结构特点共同决定
【解析】选C。物体做阻尼振动时,如果有恰当的能量补充,也可以保持振幅不变,做等幅振动,所以阻尼振动的振幅是不一定改变的,所以A错误。物体做阻尼振动时,振幅虽然不断减小,但是振动的频率仍由自身的结构特点所决定,不随振幅的减小而变化,所以B错误。受迫振动稳定时的频率,只是取决于驱动力的频率,与物体自身结构特点无关,即与物体的固有频率无关,所以D错误,C正确。
2.下列关于机械振动的说法正确的是 ( )
A.受迫振动稳定后,其振动的周期总等于系统的固有周期
B.阻尼振动振幅逐渐减小时,周期也逐渐减小
C.当驱动力的频率等于振动系统的固有频率时,受迫振动的振幅最大
D.为避免共振现象发生,应使驱动力频率接近或等于振动系统的固有频率
【解析】选C。受迫振动稳定后,其振动的周期总等于驱动力的周期,选项A错误;阻尼振动振幅逐渐减小时,周期不变,选项B错误;当驱动力的频率等于振动系统的固有频率时,产生共振,此时受迫振动的振幅最大,选项C正确;为避免共振现象发生,应使驱动力频率远离振动系统的固有频率,故选项D错误。
3.如图甲所示,竖直圆盘转动时,可带动固定在圆盘上的T形支架在竖直方向振动,T形支架的下面系着一个弹簧和小球,共同组成一个振动系统。当圆盘静止时,小球可稳定振动。现使圆盘以4 s的周期匀速转动,经过一段时间后,小球振动达到稳定。改变圆盘匀速转动的周期,其共振曲线(振幅A与驱动力的频率f的关系)如图乙所示,则 ( )
A.此振动系统的固有频率约为0.25 Hz
B.此振动系统的固有频率约为3 Hz
C.若圆盘匀速转动的周期增大,系统振动的频率不变
D.若圆盘匀速转动的周期增大,共振曲线的峰值将向右移动
【解析】选B。由振子的共振曲线可得,此振动系统的固有频率约为3 Hz,故B正确,A错误;振动系统的振动频率是由驱动力的频率决定的,所以若圆盘匀速转动的周期增大,系统的振动频率减小,故C错误;共振曲线的峰值表示振子的固有频率,它是由振动系统本身的性质决定的,与驱动力的频率无关,故D错误。
4.如图甲所示,在一条张紧的绳子上挂几个摆,当a摆振动的时候,通过张紧的绳子给其他各摆施加驱动力,使其余各摆也振动起来,达到稳定时b摆和c摆的周期大小关系是:Tb________Tc,两个摆中________摆的振幅大,图乙是c摆稳定以后的振动图像,重力加速度为g,不计空气阻力,则a摆的摆长为________。
【解析】a摆摆动起来后,通过水平绳子对b、c两个摆施加周期性的驱动力,使b、
c两摆做受迫振动,两摆做受迫振动的频率等于驱动力的频率,由于驱动力频率相
同,则两摆的周期相同;受迫振动中,当固有频率等于驱动力频率时,出现共振现
象,振幅达到最大,由于c摆的固有频率与a摆的相同,故c摆发生共振,振幅最大;
a摆的固有周期与c摆的相同,由图乙可知,振动周期为:T=t0,由单摆周期公式T=
2π 即t0=2π ,知摆长为:L= 。
答案:= c
同课章节目录
- 第1章 动量及其守恒定律
- 第1节 动量和动量定理
- 第2节 动量守恒定律及其应用
- 第3节 科学验证:动量守恒定律
- 第4节 弹性碰撞与非弹性碰撞
- 第2章 机械振动
- 第1节 简谐运动
- 第2节 振动的描述
- 第3节 单摆
- 第4节 科学测量:用单摆测量重力加速度
- 第5节 生活中的振动
- 第3章 机械波
- 第1节 波的形成和描述
- 第2节 波的反射和折射
- 第3节 波的干涉和衍射
- 第4节 多普勒效应及其应用
- 第4章 光的折射和全反射
- 第1节 光的折射
- 第2节 科学测量:玻璃的折射率
- 第3节 光的全反射
- 第4节 光导纤维及其应用
- 第5章 光的干涉、衍射和偏振
- 第1节 光的干涉
- 第2节 科学测量:用双缝干涉测光的波长
- 第3节 光的衍射
- 第4节 光的偏振
- 第5节 激光与全息照相
