4.1 光的折射课件(45张PPT)
文档属性
| 名称 | 4.1 光的折射课件(45张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 837.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-11-26 00:00:00 | ||
图片预览










文档简介
(共45张PPT)
第4章 光的折射和全反射
第1节 光 的 折 射
一、探究折射角与入射角的关系
1.光的折射:光从一种介质斜射入另一种介质时,传播方向会_____,
这种现象叫作光的折射。
2.各光线的位置:折射光线、入射光线和法线在_____(选填“同一”或
“不同”)平面内,折射光线和入射光线分别位于_____两侧。
二、光的折射定律
1.折射定律:
(1)内容:入射角的_____与折射角的_____之比是一个常数,这个关系称为光的折
射定律,也叫___________。
(2)表达式: =n。
改变
同一
法线
正弦
正弦
斯涅耳定律
2.介质的折射率:光从真空射入某种介质发生折射时,入射角i的正弦与折射角
r的正弦的______。也称为___________。
3.光路可逆:与_____现象一样,在折射现象中,光路也是可逆的。
比值n
绝对折射率
反射
三、折射率
【思考】
光从空气斜射入不同介质中时,光的偏折程度相同吗
提示:从空气斜射入不同介质中时,光的偏折程度一般不同。
1.折射率的意义:不同介质的折射率不同,介质的折射率反映了光在介质中的
_____程度。
2.折射率与光速的关系:某种介质的折射率,等于光在真空中的传播速度c与光
在这种介质中的传播速度v_____,即n= 。
3.绝对折射率和相对折射率:
(1)相对折射率:设光由介质1进入介质2,这时的折射率叫作介质2对介质1的相
对折射率,通常用n21表示,则 =n21。
(2)相对折射率与绝对折射率的关系:n21= ,其中n1和n2分别是介质1和介质
2的绝对折射率。
(3)折射率的另一种表达式:n1sini=n2sinr。
偏折
之比
关键能力·素养形成
一 折射定律的含义
对折射定律内容的认识:
(1)“同面内”:“折射光线、入射光线和法线在同一平面内”,这句话大体上说明了三线的空间位置:折射光线在入射光线与法线决定的平面内,即三线共面。
(2)“线两旁”:“折射光线和入射光线分别位于法线两侧”,这句话把折射光线的位置又作了进一步的确定,使得折射光线的“自由度”越来越小。
(3)“正比律”:“入射角的正弦与折射角的正弦之比是一个常数,即 =n”,
折射角r随入射角i的变化而变化,入射角i的正弦与折射角r的正弦之比是定
值。当入射光线的位置、方向确定下来时,折射光线的位置、方向就确定了。
(4)“正弦值”:当光由真空射入某种介质时,入射角、折射角以及它们的正弦
值是可以改变的,但入射角与折射角的正弦值的比值是一个常数。
【思考·讨论】
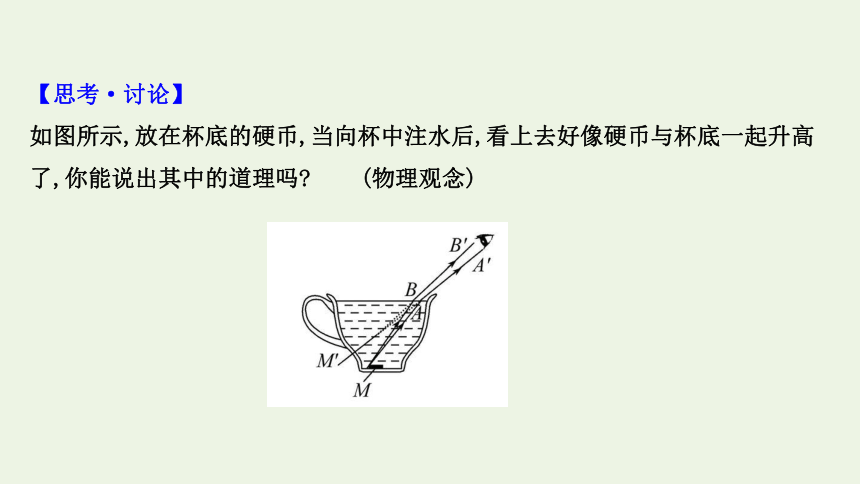
如图所示,放在杯底的硬币,当向杯中注水后,看上去好像硬币与杯底一起升高了,你能说出其中的道理吗 (物理观念)
提示:这是由于硬币M上一点发出的两条光线MA、MB分别在水面发生了折射,两条折射光线的反向延长线相交在M′点。所以,眼睛所看到的是硬币的虚像,它离水面的距离比真实硬币离水面的距离更近一些。
【典例示范】
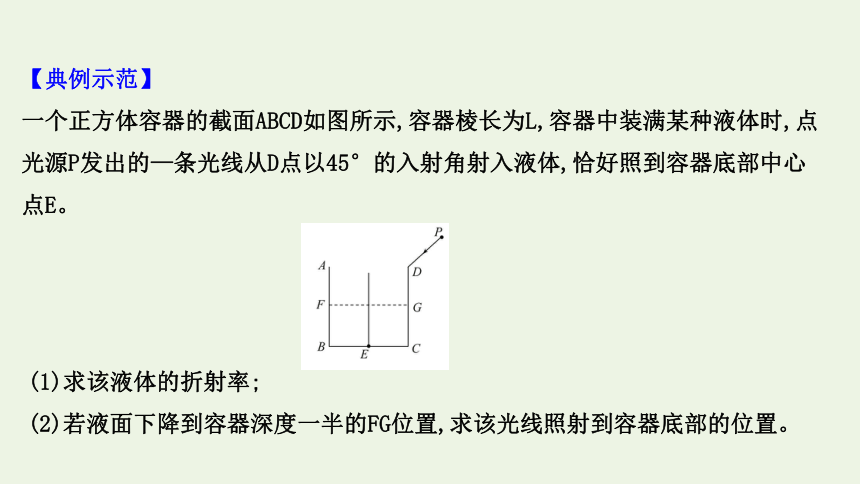
一个正方体容器的截面ABCD如图所示,容器棱长为L,容器中装满某种液体时,点光源P发出的—条光线从D点以45°的入射角射入液体,恰好照到容器底部中心点E。
(1)求该液体的折射率;
(2)若液面下降到容器深度一半的FG位置,求该光线照射到容器底部的位置。
【解题探究】
(1)光的折射定律的内容是什么
提示:n= 。
(2)光的折射率和什么有关
提示:光的折射率与介质有关。不同介质的折射率一般不同。
【解析】(1)由几何关系可知,折射角的正弦值:
sinr=
折射率:n=
(2)若液面下降到容器深度一半的FG位置,则光路如图。
则折射角仍为r,由相似三角形关系可知GE= EC,
则光线照射到容器底部的位置距离E点 L。
答案:(1) (2) L
【素养训练】
1.单色光线由某种介质射向该介质与空气的交界面,当入射角为30°时,折射光
线与反射光线刚好垂直,则该介质对该种色光的折射率为 ( )
A.2 B. C.1.5 D.
【解析】选D。当入射角i=30°时,折射光线与反射光线恰好垂直,则折射角
r=90°-30°=60°,该介质对该种色光的折射率为n= ,故选项D正
确,A、B、C错误。
2.如图所示,一条光线通过一个在水中的球形空气泡,下列哪一条表示出射光线
的路径 ( )
A.光线1
B.光线2
C.光线3
D.光线4
【解析】选A。光先从水进入空气泡中,由折射定律可知折射角应大于入射角;然后又从空气射入水中,折射角应小于入射角。所以选A。
3.(2016·江苏高考)人造树脂是常用的眼镜镜片材料。如图所示,光线射在一人造树脂立方体上,经折射后,射在桌面上的P点。已知光线的入射角为30°,OA=5 cm,AB=20 cm,BP=12 cm,求该人造树脂材料的折射率n。
【解析】设折射角为γ,由折射定律,sin30°=nsinγ
由几何关系知sinγ= ,
且OP=
代入数据解得n=1.5
答案:1.5
【补偿训练】
一束单色光由空气射入玻璃,这束光的 ( )
A.速度变慢,波长变短 B.速度不变,波长变短
C.频率增高,波长变长 D.频率不变,波长变长
【解析】选A。玻璃的折射率n= >1,所以光经空气射入玻璃速度减小。波
长、波速和频率三者的关系是v=λf,光经空气进入玻璃,频率f不变,波长变
短。所以A正确。
二 折射率的特点
对折射率特点的认识:
(1)折射率大小不仅反映了介质的折射本领,也反映了光在介质中传播速度的大
小。不同介质具有不同的折射率,说明折射率反映了该介质的光学特性。
(2)介质的折射率是反映介质的光学性质的物理量,它的大小只能由介质本身及
光的性质共同决定,不随入射角、折射角的变化而变化。
(3)介质的折射率n跟光在其中的传播速度v有关,即n= 。由于光在真空中的
传播速度c大于光在任何介质中的传播速度v,所以任何介质的折射率n都大于
1。因此,光从真空斜射入任何介质时,入射角均大于折射角;而光由介质斜射入
真空时,入射角均小于折射角。
【思考·讨论】
有经验的渔民叉鱼时,不是正对着看到的鱼去叉,而是对着所看到鱼的下方叉,如图所示。你知道这是为什么吗 (物理观念)
提示:从鱼身上反射的光线由水中进入空气时,在水面上发生折射,折射角大于入射角,折射光线进入人眼,人眼会逆着折射光线的方向看去,就会觉得鱼变浅了,眼睛看到的是鱼的虚像,在鱼的上方,所以叉鱼时要瞄准像的下方,如图所示。
【典例示范】
如图所示,一个截面为矩形的水池,池底有一垂直于池壁的线形发光体,长度
l=3 m,当池中未装水时,一高h=1.5 m的人站在距池边s1=2 m的A点,只能看到
发光体的左端点①。当将水池加满水时,人需移动到距池边s2=3 m的B点时,
才只能看到发光体的左端点②。已知发光体的右端紧靠站人一方的池边,人站
的位置与发光体在同一竖直面内,不计人眼到头顶的距离。求:
(1)水池中水的折射率③ ;
(2)人站在B点时看到的左端点的像到发光体的距离。
【审题关键】
序号 信息提取
① 可求入射角的正弦值
② 可求折射角的正弦值
③ 折射率n=
【解析】(1)光路如图所示:
当水池中装满水,光从发光体的左端点发出的光射到站在B处的人的眼睛中时,
对应的入射角的正弦值为sini=
对应的折射角的正弦值为sinr=
故水池中水的折射率n=
解得:n=
(2)设水池深度为H, 当人站在A点时,
解得:H=2.25 m
设左端点的像到水面的距离为x,则有:
解得:x=1.5 m
则左端点的像到发光体的距离为H-x=0.75 m。
答案:(1) (2)0.75 m
【规律方法】利用光路图解决光的折射问题的步骤
(1)根据题意画出正确的光路图。首先要找到入射的界面,同时准确地作出法线,
再根据折射定律和入射光线画出折射光线,找到入射角和折射角,要注意入射角、
折射角是入射光线、折射光线与法线的夹角。
(2)利用几何关系确定光路图中的边、角关系,与折射定律n= 中的各量准确
对应。
(3)利用折射定律n= 、折射率与光速的关系n= 列方程,结合数学三角函
数的知识进行运算。
【素养训练】
1.(多选)如图所示,一束复色光由空气射向一块两面平行的玻璃砖,经折射后分为两束单色光a和b,下列判断正确的是 ( )
A.a光的频率小于b光的频率
B.在玻璃砖中a光的波长小于b光的波长
C.若单色光a是蓝光,则b可能是紫光
D.单色光a和b从下表面射出时一定平行
【解析】选B、D。复色光进入玻璃砖时两光的入射角i相等,设折射角分别为
ra、rb,由图知,ranb,则fa>fb,故A错误;在玻璃砖中v= 、
v=λf,则在玻璃砖中波长λ= ,得λa<λb,故B正确;因为fa>fb,所以若
单色光a是蓝光,则b不可能是紫光,故C错误;由光路可逆原理可知,离开玻璃砖
时与进入玻璃砖时光线平行,故D正确。
2.(多选)井口大小和深度相同的两口井,一口是枯井,一口是水井(水面在井口之下),两井底部中心处各有一只青蛙,则( )
A.枯井中的青蛙觉得井口大些
B.水井中的青蛙觉得井口大些
C.晴天的夜晚,枯井中的青蛙能看到更多的星星
D.晴天的夜晚,水井中的青蛙能看到更多的星星
【解析】选A、D。作出光路图(如图所示)
可知,枯井中的青蛙觉得井口大些,A符合题
意,B不符合题意;晴天的夜晚,水井中的青蛙
能看到更多的星星,C不符合题意,D符合题意。
3.如图所示,一根竖直插入水中的杆AB,在水中部分长1.0 m,露出水面部分长
0.3 m,已知水的折射率为 ,则当阳光与水平面成37°角时,杆AB在水下的影
长为多少 (sin37°=0.6,cos37°=0.8)
【解析】光路如图所示
由题意可得入射角为53°
由折射定律 =n,
,则r=37°,
由几何关系得影长
s=0.3 m×tan53°+1 m×tan37°=1.15 m
答案:1.15 m
【拓展例题】考查内容:折射率的计算
【典例】如图,置于空气中的一不透明容
器内盛满某种透明液体。容器底部靠近器
壁处有一竖直放置的6.0 cm长的线光源。靠近线光源一侧的液面上盖有一遮光
板,另一侧有一水平放置的与液面等高的望远镜,用来观察线光源。开始时通过
望远镜不能看到线光源的任何一部分。将线光源沿容器底向望远镜一侧平移至
某处时,通过望远镜刚好可以看到线光源底端,再将线光源沿同一方向移动
8.0 cm,刚好可以看到其顶端,求此液体的折射率n。
【解析】
若线光源底端在A点时,望远镜刚好可看到线光源的底端,
则有:∠AOO′=α其中α为此液体到空气的全反射临界角,
由折射定律得:sinα= 同理,线光源顶端在B1点时,
望远镜刚好可看到线光源的顶端,则∠B1OO′=α
由图中几何关系得:sinα=
解得:n= =1.25
答案:1.25
【课堂回眸】
课堂检测·素养达标
1.(多选)关于光的折射和折射率,下列说法正确的是 ( )
A.折射光与入射光的传播方向总是不同的
B.发生折射是因为光在不同介质中的传播速度不同
C.根据n= 可知,介质的折射率与入射角的正弦成正比
D.介质的折射率总是大于1
【解析】选B、D。发生折射现象是由于光在不同介质中传播速度不同,当光线
垂直入射到介质分界面上时,折射光与入射光方向相同,故A不符合题意,B符合
题意;折射率由介质决定,与入射角无关,C不符合题意;介质折射率n= ,又光
在介质中的速度小于光在空气(真空)中的速度,所以介质折射率总大于1,D符合
题意。
2.(多选)如图所示,实线为空气和水的分界面,一束绿光从水中的A点沿AO1方向(O1点在分界面上,图中O1点和入射光线都未画出)射向空气中,折射后通过空气中的B点(图中折射光线也未画出)。图中O点为A、B连线与分界面的交点。下列说法正确的是 ( )
A.O1点在O点的左侧
B.绿光从水中射入空气中时,速度变小
C.若绿光沿AO方向射向空气中,则折射光线有可能 通过B点正下方的C点
D.若沿AO1方向射向空气中的是一束紫光,则折射光线也有可能通过B点
【解析】选A、C。当光由水中射入空气中时入射角
小于折射角,画出大致光路图如图所示,可见O1点在
O点的左侧,故A正确。光在真空中速度最大,当绿光从水中射入空气中时,速度
变大,故B错误。若绿光沿AO方向射向空气中,则入射角变大,折射角也变大,折
射光线有可能通过B点正下方的C点,选项C正确;若沿AO1方向射向空气中的是一
束紫光,因紫光的折射率大于绿光,可知折射光线通过B点下方,选项D错误。
3.经研究发现:空气的折射率大于1,并且离地球表面越近,大气层的密度越大,折射率越大,假设地球表面不存在大气层,那么人们观察到的日出时刻与实际存在大气层时的情况相比 ( )
A.将提前
B.将延后
C.某些区域提前,在另一些区域延后
D.不变
【解析】选B。若地球表面不存在大气层,太阳光将在真空中沿直线传播,由于地球是圆形的,所以只有太阳升到某一位置时才能观察到;而正因为地球表面上有大气层,太阳光射入大气层时会发生折射现象,能够提前观察到;所以如果地球表面不存在大气层,那么观察到的日出时刻与实际存在大气层时的情况相比将延后。故选B。
4.(2018·全国卷Ⅲ)如图,某同学在一张水平放置的
白纸上画了一个小标记“ ”(图中O点),然后用横截
面为等边三角形ABC的三棱镜压在这个标记上,小标记
位于AC边上。D位于AB边上,过D点作AC边的垂线交AC于F。该同学在D点正上方
向下顺着直线DF的方向观察,恰好可以看到小标记的像;过O点作AB边的垂线交
直线DF于E;DE=2 cm,EF=1 cm。求三棱镜的折射率。(不考虑光线在三棱镜中的
反射)
【解析】
作出光路如图所示
据折射定律n= ,
由于DE=2 cm,∠FDA=30°
因此EH=1 cm,
则据几何关系可知OD∥BC,
因此β=30°,θ=60°,解得三棱镜的折射率n= 。
答案:
第4章 光的折射和全反射
第1节 光 的 折 射
一、探究折射角与入射角的关系
1.光的折射:光从一种介质斜射入另一种介质时,传播方向会_____,
这种现象叫作光的折射。
2.各光线的位置:折射光线、入射光线和法线在_____(选填“同一”或
“不同”)平面内,折射光线和入射光线分别位于_____两侧。
二、光的折射定律
1.折射定律:
(1)内容:入射角的_____与折射角的_____之比是一个常数,这个关系称为光的折
射定律,也叫___________。
(2)表达式: =n。
改变
同一
法线
正弦
正弦
斯涅耳定律
2.介质的折射率:光从真空射入某种介质发生折射时,入射角i的正弦与折射角
r的正弦的______。也称为___________。
3.光路可逆:与_____现象一样,在折射现象中,光路也是可逆的。
比值n
绝对折射率
反射
三、折射率
【思考】
光从空气斜射入不同介质中时,光的偏折程度相同吗
提示:从空气斜射入不同介质中时,光的偏折程度一般不同。
1.折射率的意义:不同介质的折射率不同,介质的折射率反映了光在介质中的
_____程度。
2.折射率与光速的关系:某种介质的折射率,等于光在真空中的传播速度c与光
在这种介质中的传播速度v_____,即n= 。
3.绝对折射率和相对折射率:
(1)相对折射率:设光由介质1进入介质2,这时的折射率叫作介质2对介质1的相
对折射率,通常用n21表示,则 =n21。
(2)相对折射率与绝对折射率的关系:n21= ,其中n1和n2分别是介质1和介质
2的绝对折射率。
(3)折射率的另一种表达式:n1sini=n2sinr。
偏折
之比
关键能力·素养形成
一 折射定律的含义
对折射定律内容的认识:
(1)“同面内”:“折射光线、入射光线和法线在同一平面内”,这句话大体上说明了三线的空间位置:折射光线在入射光线与法线决定的平面内,即三线共面。
(2)“线两旁”:“折射光线和入射光线分别位于法线两侧”,这句话把折射光线的位置又作了进一步的确定,使得折射光线的“自由度”越来越小。
(3)“正比律”:“入射角的正弦与折射角的正弦之比是一个常数,即 =n”,
折射角r随入射角i的变化而变化,入射角i的正弦与折射角r的正弦之比是定
值。当入射光线的位置、方向确定下来时,折射光线的位置、方向就确定了。
(4)“正弦值”:当光由真空射入某种介质时,入射角、折射角以及它们的正弦
值是可以改变的,但入射角与折射角的正弦值的比值是一个常数。
【思考·讨论】
如图所示,放在杯底的硬币,当向杯中注水后,看上去好像硬币与杯底一起升高了,你能说出其中的道理吗 (物理观念)
提示:这是由于硬币M上一点发出的两条光线MA、MB分别在水面发生了折射,两条折射光线的反向延长线相交在M′点。所以,眼睛所看到的是硬币的虚像,它离水面的距离比真实硬币离水面的距离更近一些。
【典例示范】
一个正方体容器的截面ABCD如图所示,容器棱长为L,容器中装满某种液体时,点光源P发出的—条光线从D点以45°的入射角射入液体,恰好照到容器底部中心点E。
(1)求该液体的折射率;
(2)若液面下降到容器深度一半的FG位置,求该光线照射到容器底部的位置。
【解题探究】
(1)光的折射定律的内容是什么
提示:n= 。
(2)光的折射率和什么有关
提示:光的折射率与介质有关。不同介质的折射率一般不同。
【解析】(1)由几何关系可知,折射角的正弦值:
sinr=
折射率:n=
(2)若液面下降到容器深度一半的FG位置,则光路如图。
则折射角仍为r,由相似三角形关系可知GE= EC,
则光线照射到容器底部的位置距离E点 L。
答案:(1) (2) L
【素养训练】
1.单色光线由某种介质射向该介质与空气的交界面,当入射角为30°时,折射光
线与反射光线刚好垂直,则该介质对该种色光的折射率为 ( )
A.2 B. C.1.5 D.
【解析】选D。当入射角i=30°时,折射光线与反射光线恰好垂直,则折射角
r=90°-30°=60°,该介质对该种色光的折射率为n= ,故选项D正
确,A、B、C错误。
2.如图所示,一条光线通过一个在水中的球形空气泡,下列哪一条表示出射光线
的路径 ( )
A.光线1
B.光线2
C.光线3
D.光线4
【解析】选A。光先从水进入空气泡中,由折射定律可知折射角应大于入射角;然后又从空气射入水中,折射角应小于入射角。所以选A。
3.(2016·江苏高考)人造树脂是常用的眼镜镜片材料。如图所示,光线射在一人造树脂立方体上,经折射后,射在桌面上的P点。已知光线的入射角为30°,OA=5 cm,AB=20 cm,BP=12 cm,求该人造树脂材料的折射率n。
【解析】设折射角为γ,由折射定律,sin30°=nsinγ
由几何关系知sinγ= ,
且OP=
代入数据解得n=1.5
答案:1.5
【补偿训练】
一束单色光由空气射入玻璃,这束光的 ( )
A.速度变慢,波长变短 B.速度不变,波长变短
C.频率增高,波长变长 D.频率不变,波长变长
【解析】选A。玻璃的折射率n= >1,所以光经空气射入玻璃速度减小。波
长、波速和频率三者的关系是v=λf,光经空气进入玻璃,频率f不变,波长变
短。所以A正确。
二 折射率的特点
对折射率特点的认识:
(1)折射率大小不仅反映了介质的折射本领,也反映了光在介质中传播速度的大
小。不同介质具有不同的折射率,说明折射率反映了该介质的光学特性。
(2)介质的折射率是反映介质的光学性质的物理量,它的大小只能由介质本身及
光的性质共同决定,不随入射角、折射角的变化而变化。
(3)介质的折射率n跟光在其中的传播速度v有关,即n= 。由于光在真空中的
传播速度c大于光在任何介质中的传播速度v,所以任何介质的折射率n都大于
1。因此,光从真空斜射入任何介质时,入射角均大于折射角;而光由介质斜射入
真空时,入射角均小于折射角。
【思考·讨论】
有经验的渔民叉鱼时,不是正对着看到的鱼去叉,而是对着所看到鱼的下方叉,如图所示。你知道这是为什么吗 (物理观念)
提示:从鱼身上反射的光线由水中进入空气时,在水面上发生折射,折射角大于入射角,折射光线进入人眼,人眼会逆着折射光线的方向看去,就会觉得鱼变浅了,眼睛看到的是鱼的虚像,在鱼的上方,所以叉鱼时要瞄准像的下方,如图所示。
【典例示范】
如图所示,一个截面为矩形的水池,池底有一垂直于池壁的线形发光体,长度
l=3 m,当池中未装水时,一高h=1.5 m的人站在距池边s1=2 m的A点,只能看到
发光体的左端点①。当将水池加满水时,人需移动到距池边s2=3 m的B点时,
才只能看到发光体的左端点②。已知发光体的右端紧靠站人一方的池边,人站
的位置与发光体在同一竖直面内,不计人眼到头顶的距离。求:
(1)水池中水的折射率③ ;
(2)人站在B点时看到的左端点的像到发光体的距离。
【审题关键】
序号 信息提取
① 可求入射角的正弦值
② 可求折射角的正弦值
③ 折射率n=
【解析】(1)光路如图所示:
当水池中装满水,光从发光体的左端点发出的光射到站在B处的人的眼睛中时,
对应的入射角的正弦值为sini=
对应的折射角的正弦值为sinr=
故水池中水的折射率n=
解得:n=
(2)设水池深度为H, 当人站在A点时,
解得:H=2.25 m
设左端点的像到水面的距离为x,则有:
解得:x=1.5 m
则左端点的像到发光体的距离为H-x=0.75 m。
答案:(1) (2)0.75 m
【规律方法】利用光路图解决光的折射问题的步骤
(1)根据题意画出正确的光路图。首先要找到入射的界面,同时准确地作出法线,
再根据折射定律和入射光线画出折射光线,找到入射角和折射角,要注意入射角、
折射角是入射光线、折射光线与法线的夹角。
(2)利用几何关系确定光路图中的边、角关系,与折射定律n= 中的各量准确
对应。
(3)利用折射定律n= 、折射率与光速的关系n= 列方程,结合数学三角函
数的知识进行运算。
【素养训练】
1.(多选)如图所示,一束复色光由空气射向一块两面平行的玻璃砖,经折射后分为两束单色光a和b,下列判断正确的是 ( )
A.a光的频率小于b光的频率
B.在玻璃砖中a光的波长小于b光的波长
C.若单色光a是蓝光,则b可能是紫光
D.单色光a和b从下表面射出时一定平行
【解析】选B、D。复色光进入玻璃砖时两光的入射角i相等,设折射角分别为
ra、rb,由图知,ra
v=λf,则在玻璃砖中波长λ= ,得λa<λb,故B正确;因为fa>fb,所以若
单色光a是蓝光,则b不可能是紫光,故C错误;由光路可逆原理可知,离开玻璃砖
时与进入玻璃砖时光线平行,故D正确。
2.(多选)井口大小和深度相同的两口井,一口是枯井,一口是水井(水面在井口之下),两井底部中心处各有一只青蛙,则( )
A.枯井中的青蛙觉得井口大些
B.水井中的青蛙觉得井口大些
C.晴天的夜晚,枯井中的青蛙能看到更多的星星
D.晴天的夜晚,水井中的青蛙能看到更多的星星
【解析】选A、D。作出光路图(如图所示)
可知,枯井中的青蛙觉得井口大些,A符合题
意,B不符合题意;晴天的夜晚,水井中的青蛙
能看到更多的星星,C不符合题意,D符合题意。
3.如图所示,一根竖直插入水中的杆AB,在水中部分长1.0 m,露出水面部分长
0.3 m,已知水的折射率为 ,则当阳光与水平面成37°角时,杆AB在水下的影
长为多少 (sin37°=0.6,cos37°=0.8)
【解析】光路如图所示
由题意可得入射角为53°
由折射定律 =n,
,则r=37°,
由几何关系得影长
s=0.3 m×tan53°+1 m×tan37°=1.15 m
答案:1.15 m
【拓展例题】考查内容:折射率的计算
【典例】如图,置于空气中的一不透明容
器内盛满某种透明液体。容器底部靠近器
壁处有一竖直放置的6.0 cm长的线光源。靠近线光源一侧的液面上盖有一遮光
板,另一侧有一水平放置的与液面等高的望远镜,用来观察线光源。开始时通过
望远镜不能看到线光源的任何一部分。将线光源沿容器底向望远镜一侧平移至
某处时,通过望远镜刚好可以看到线光源底端,再将线光源沿同一方向移动
8.0 cm,刚好可以看到其顶端,求此液体的折射率n。
【解析】
若线光源底端在A点时,望远镜刚好可看到线光源的底端,
则有:∠AOO′=α其中α为此液体到空气的全反射临界角,
由折射定律得:sinα= 同理,线光源顶端在B1点时,
望远镜刚好可看到线光源的顶端,则∠B1OO′=α
由图中几何关系得:sinα=
解得:n= =1.25
答案:1.25
【课堂回眸】
课堂检测·素养达标
1.(多选)关于光的折射和折射率,下列说法正确的是 ( )
A.折射光与入射光的传播方向总是不同的
B.发生折射是因为光在不同介质中的传播速度不同
C.根据n= 可知,介质的折射率与入射角的正弦成正比
D.介质的折射率总是大于1
【解析】选B、D。发生折射现象是由于光在不同介质中传播速度不同,当光线
垂直入射到介质分界面上时,折射光与入射光方向相同,故A不符合题意,B符合
题意;折射率由介质决定,与入射角无关,C不符合题意;介质折射率n= ,又光
在介质中的速度小于光在空气(真空)中的速度,所以介质折射率总大于1,D符合
题意。
2.(多选)如图所示,实线为空气和水的分界面,一束绿光从水中的A点沿AO1方向(O1点在分界面上,图中O1点和入射光线都未画出)射向空气中,折射后通过空气中的B点(图中折射光线也未画出)。图中O点为A、B连线与分界面的交点。下列说法正确的是 ( )
A.O1点在O点的左侧
B.绿光从水中射入空气中时,速度变小
C.若绿光沿AO方向射向空气中,则折射光线有可能 通过B点正下方的C点
D.若沿AO1方向射向空气中的是一束紫光,则折射光线也有可能通过B点
【解析】选A、C。当光由水中射入空气中时入射角
小于折射角,画出大致光路图如图所示,可见O1点在
O点的左侧,故A正确。光在真空中速度最大,当绿光从水中射入空气中时,速度
变大,故B错误。若绿光沿AO方向射向空气中,则入射角变大,折射角也变大,折
射光线有可能通过B点正下方的C点,选项C正确;若沿AO1方向射向空气中的是一
束紫光,因紫光的折射率大于绿光,可知折射光线通过B点下方,选项D错误。
3.经研究发现:空气的折射率大于1,并且离地球表面越近,大气层的密度越大,折射率越大,假设地球表面不存在大气层,那么人们观察到的日出时刻与实际存在大气层时的情况相比 ( )
A.将提前
B.将延后
C.某些区域提前,在另一些区域延后
D.不变
【解析】选B。若地球表面不存在大气层,太阳光将在真空中沿直线传播,由于地球是圆形的,所以只有太阳升到某一位置时才能观察到;而正因为地球表面上有大气层,太阳光射入大气层时会发生折射现象,能够提前观察到;所以如果地球表面不存在大气层,那么观察到的日出时刻与实际存在大气层时的情况相比将延后。故选B。
4.(2018·全国卷Ⅲ)如图,某同学在一张水平放置的
白纸上画了一个小标记“ ”(图中O点),然后用横截
面为等边三角形ABC的三棱镜压在这个标记上,小标记
位于AC边上。D位于AB边上,过D点作AC边的垂线交AC于F。该同学在D点正上方
向下顺着直线DF的方向观察,恰好可以看到小标记的像;过O点作AB边的垂线交
直线DF于E;DE=2 cm,EF=1 cm。求三棱镜的折射率。(不考虑光线在三棱镜中的
反射)
【解析】
作出光路如图所示
据折射定律n= ,
由于DE=2 cm,∠FDA=30°
因此EH=1 cm,
则据几何关系可知OD∥BC,
因此β=30°,θ=60°,解得三棱镜的折射率n= 。
答案:
同课章节目录
- 第1章 动量及其守恒定律
- 第1节 动量和动量定理
- 第2节 动量守恒定律及其应用
- 第3节 科学验证:动量守恒定律
- 第4节 弹性碰撞与非弹性碰撞
- 第2章 机械振动
- 第1节 简谐运动
- 第2节 振动的描述
- 第3节 单摆
- 第4节 科学测量:用单摆测量重力加速度
- 第5节 生活中的振动
- 第3章 机械波
- 第1节 波的形成和描述
- 第2节 波的反射和折射
- 第3节 波的干涉和衍射
- 第4节 多普勒效应及其应用
- 第4章 光的折射和全反射
- 第1节 光的折射
- 第2节 科学测量:玻璃的折射率
- 第3节 光的全反射
- 第4节 光导纤维及其应用
- 第5章 光的干涉、衍射和偏振
- 第1节 光的干涉
- 第2节 科学测量:用双缝干涉测光的波长
- 第3节 光的衍射
- 第4节 光的偏振
- 第5节 激光与全息照相
