旋转导学案(无答案)
图片预览


文档简介
23.1 图形的旋转(1)(总第一课时)计划上课时间
主备 王宇齐 审阅 审批
一、学习目标:
1、通过具体实例认识图形的旋转,理解“对应点到旋转中心的距离相等”以及“旋转前、后的图形全等”的基本性质。
二、学习重点:对生活中的旋转现象作数学上的分析,理解旋转的定义。
学习难点:对旋转现象进行分析研究,旋转后的现象进行探索。
三、复习和预习案:
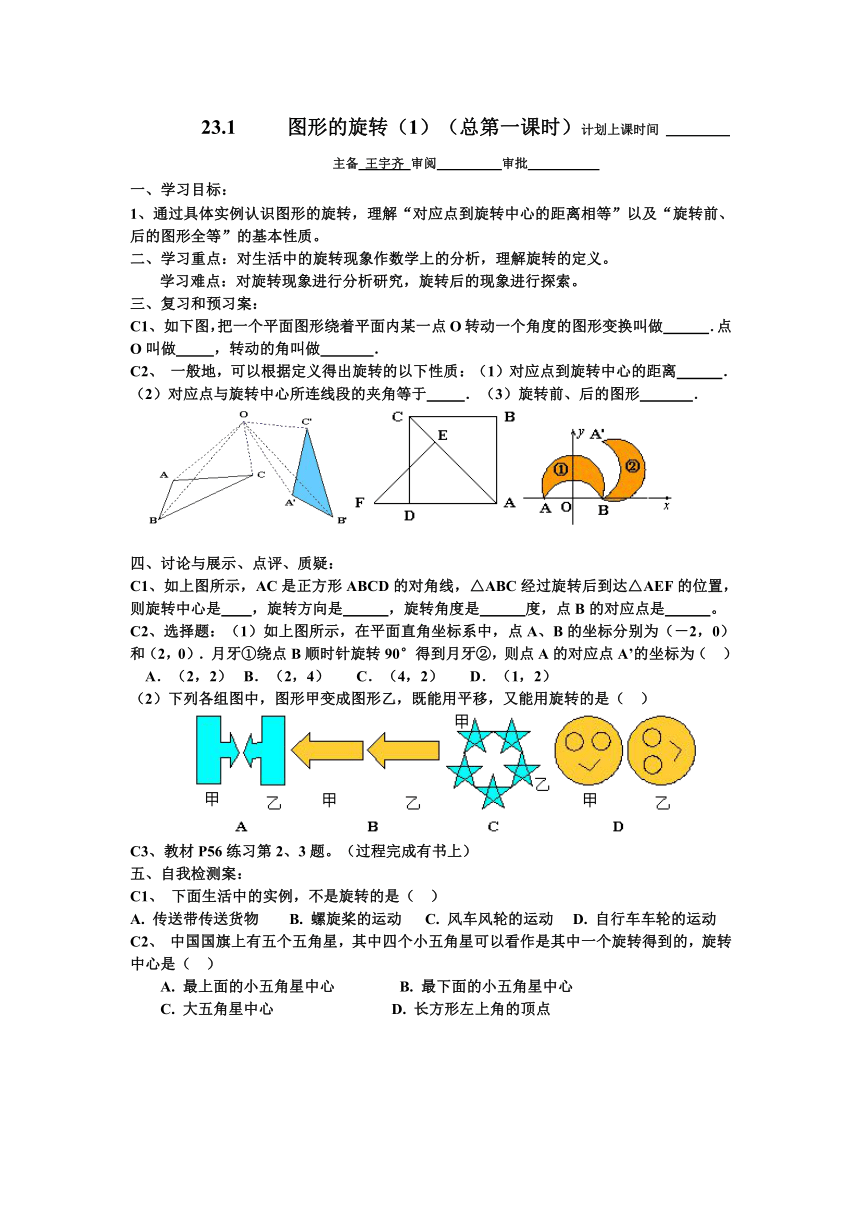
C1、 如下图,把一个平面图形绕着平面内某一点O转动一个角度的图形变换叫做 .点O叫做 ,转动的角叫做 .
C2、 一般地,可以根据定义得出旋转的以下性质:(1)对应点到旋转中心的距离 .
(2)对应点与旋转中心所连线段的夹角等于 .(3)旋转前、后的图形 .
四、讨论与展示、点评、质疑:
C1、如上图所示,AC是正方形ABCD的对角线,△ABC经过旋转后到达△AEF的位置,则旋转中心是 ,旋转方向是 ,旋转角度是 度,点B的对应点是 。
C2、选择题:(1)如上图所示,在平面直角坐标系中,点A、B的坐标分别为(-2,0)和(2,0).月牙①绕点B顺时针旋转90°得到月牙②,则点A的对应点A’的坐标为( )
A.(2,2) B.(2,4) C.(4,2) D.(1,2)
(2)下列各组图中,图形甲变成图形乙,既能用平移,又能用旋转的是( )
C3、教材P56练习第2、3题。(过程完成有书上)
五、自我检测案:
C1、 下面生活中的实例,不是旋转的是( )
A. 传送带传送货物 B. 螺旋桨的运动 C. 风车风轮的运动 D. 自行车车轮的运动
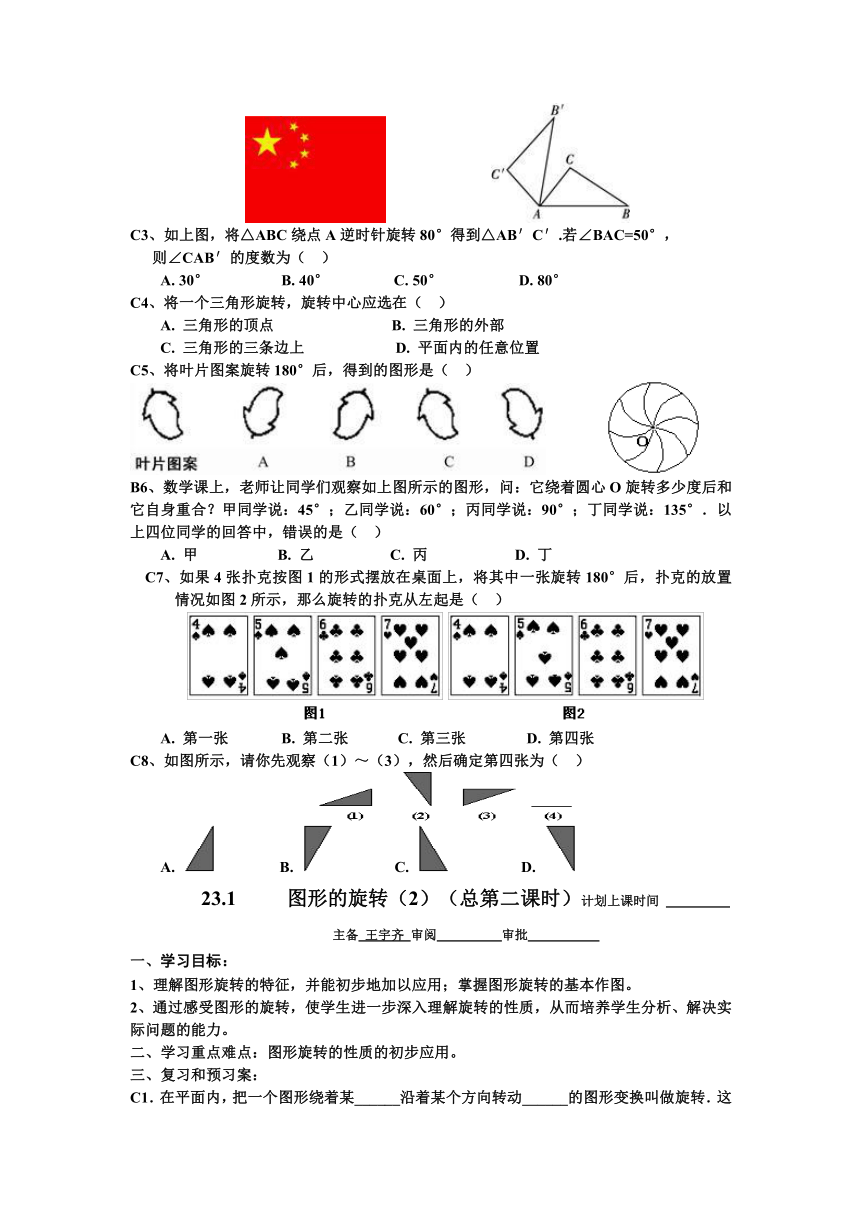
C2、 中国国旗上有五个五角星,其中四个小五角星可以看作是其中一个旋转得到的,旋转中心是( )
A. 最上面的小五角星中心 B. 最下面的小五角星中心
C. 大五角星中心 D. 长方形左上角的顶点
C3、如上图,将△ABC绕点A逆时针旋转80°得到△AB′C′.若∠BAC=50°,
则∠CAB′的度数为( )
A. 30° B. 40° C. 50° D. 80°
C4、将一个三角形旋转,旋转中心应选在( )
A. 三角形的顶点 B. 三角形的外部
C. 三角形的三条边上 D. 平面内的任意位置
C5、将叶片图案旋转180°后,得到的图形是( )
B6、数学课上,老师让同学们观察如上图所示的图形,问:它绕着圆心O旋转多少度后和它自身重合?甲同学说:45°;乙同学说:60°;丙同学说:90°;丁同学说:135°.以上四位同学的回答中,错误的是( )
A. 甲 B. 乙 C. 丙 D. 丁
C7、如果4张扑克按图1的形式摆放在桌面上,将其中一张旋转180°后,扑克的放置情况如图2所示,那么旋转的扑克从左起是( )
A. 第一张 B. 第二张 C. 第三张 D. 第四张
C8、如图所示,请你先观察(1)~(3),然后确定第四张为( )
A. B. C. D.
23.1 图形的旋转(2)(总第二课时)计划上课时间
主备 王宇齐 审阅 审批
一、学习目标:
1、理解图形旋转的特征,并能初步地加以应用;掌握图形旋转的基本作图。
2、通过感受图形的旋转,使学生进一步深入理解旋转的性质,从而培养学生分析、解决实际问题的能力。
二、学习重点难点:图形旋转的性质的初步应用。
三、复习和预习案:
C1.在平面内,把一个图形绕着某______沿着某个方向转动______的图形变换叫做旋转.这个点O叫做_____,转动的角叫做_____.因此,图形的旋转是由____ _, 以及______决定的.
C2.如果图形上的点P经过旋转变为点P′,那么这两点叫做这个旋转的______.
C3.如图,△AOB旋转到△A′OB′的位置.若∠AOA′=90°,则旋转中心是点______.旋转角是______.点A的对应点是______.线段AB的对应线段是______.∠B的对应角是______.∠BOB′=______度。
3题图 4题图
C4.如图,△ABC绕着点O旋转到△DEF的位置,则旋转中心是______.旋转角是______.AO=______,AB=______,∠ACB=∠______.
四、讨论与展示、点评、质疑:
C1、阅读教材P58--59回答问题:(1)教材中图23. 1—7是把一个图案进行 ,其中 不变,改变了 而设计的图案。教材中图23. 1—8是把一个图案进行 ,其中 不变,改变了 而设计的图案。
(2)利用旋转设计图案时,基本图形唯一吗? 。
旋转角的度数唯一吗? 。旋转中心唯一吗? 。
观察图23.1-9可知,经过旋转可以设计美丽的图案。
C2、教材P57例:(图画在右边空白处)
解:
C3、教材P58第2题:解:
C4、教材P60第4、5题完成在书上。
C5、教材P61第10题:
解:
五、自我检测案:
C1.图形之间的变换关系包括 、_______、 以及它们的组合变换.
C2.如下右图,过圆心O和图上一点A连一条曲线,将OA绕O点按同一方向连续旋转三次,每次旋转90°,把圆分成四部分,这四部分面积是圆的_________.
C3.已知:如图,F是正方形ABCD中BC边上一点,延长AB到E,使得BE=BF,试用旋转的性质说明:AF=CE且AF⊥CE.
C4、 如图所示,△ABC中,∠ACB=90°,∠BAC=30°,点D是斜边上任意一点,以A点为中心,把△ACD顺时针旋转30°,画出旋转后的图形.
C5、教材P60第7题:解:五角星的旋转角度是 或 或 或 度,在三角形的旋转角度是 或 度。
C6、教材P61第9题:解:利用等腰三角形旋转制作五角星的方法是先确定旋转为 ,旋转角度为 度,经过 次旋转可以制作而成。
C7.一个平行四边形ABCD,如果绕其对角线的交点O旋转,至少要旋转______度,才可与其自身重合.
B8.钟表的运动可以看作是一种旋转现象,那么分针匀速旋转时,它的旋转中心是钟表的旋转轴的轴心,经过45分钟分针旋转了______度.
B9. 由8时15分到8时40分,时钟的分针旋转的角度为________度,时针旋转的角度为__________度。时间和分针的夹角是 度。
B10、9点20分时针和分针的夹角是 度。
23.2.1 中心对称(一)(总第三课时)计划上课时间
主备 王宇齐 审阅 审批
一、学习目标:两个图形关于某一点对称或中心对称就是一个图形绕一点旋转180°而成。
2、掌握成中心对称的两个图形的性质,以及利用两种不同方式来作出中心对称的图形.
二、学习重点难点:中心对称的性质及初步应用.
三、复习和预习案:
C1. 图形的旋转是由_________和_________所决定的,旋转不改变图形的_____和_____.
C2. 如下图(2)可以看作是由图(1)经过______次旋转,每次旋转______度得到的.
(1) (2) (3)
C3、如上第三个图所示,某战士在训练场上练习射击,发现子弹均击中靶子上的阴影部分,那么阴影部分的面积是圆的面积的 。
C4、观察与实验:如上(1((2)(3)图,用透明纸覆盖在图上,描出其中的一部分,用大头针固定在O处。旋转180°后,你有什么发现?
发现:把一个图形绕着某一个 旋转 ,如果他们能够与另一个图形 ,那么就说这 个图形 或 ,这个点叫做 ,这两个图形中的 叫做关于中心的 .
C5、中心对称性质:(1)
(2)
四、讨论与展示、点评、质疑:
阅读教材P64例1完成下列各题:
C1、教材P64第1、2题完成在书上。
C2、教材P67第1、题完成在书上。
C3、教材P68第7题完成在书上。
五、自我检测案:
C1、已知下列命题:① 关于中心对称的两个图形一定不全等; ②关于中心对称的两个图形一定全等; ③两个全等的图形一定成中心对称,其中真命题的个数是( )
A、0 B、1 C、2 D、3
C2、下列图形即是轴对称又是中心对称的是( )
A B C C
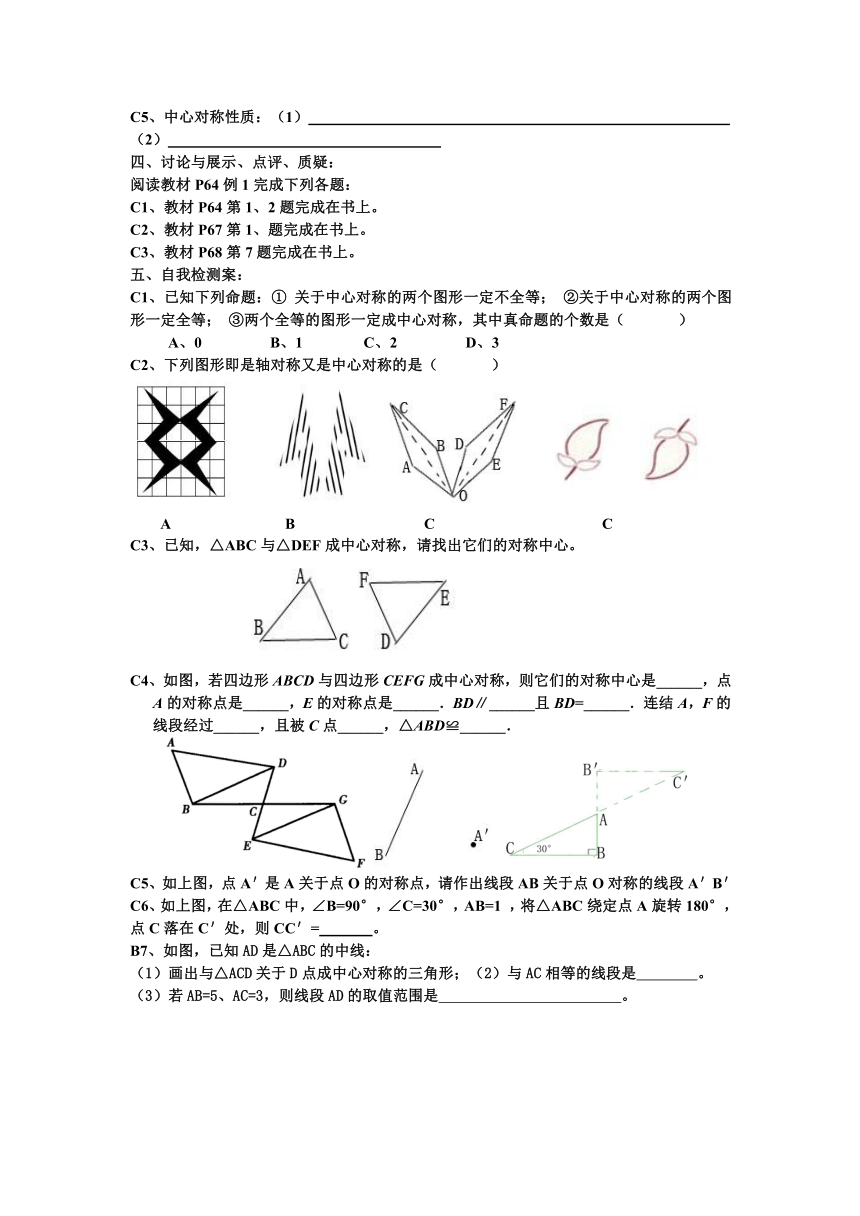
C3、已知,△ABC与△DEF成中心对称,请找出它们的对称中心。
C4、如图,若四边形ABCD与四边形CEFG成中心对称,则它们的对称中心是______,点A的对称点是______,E的对称点是______.BD∥______且BD=______.连结A,F的线段经过______,且被C点______,△ABD≌______.
C5、如上图,点A'是A关于点O的对称点,请作出线段AB关于点O对称的线段A'B'
C6、如上图,在△ABC中,∠B=90°,∠C=30°,AB=1 ,将△ABC绕定点A旋转180°,点C落在C'处,则CC'= 。
B7、如图,已知AD是△ABC的中线:
(1)画出与△ACD关于D点成中心对称的三角形;(2)与AC相等的线段是 。
(3)若AB=5、AC=3,则线段AD的取值范围是 。
23.2.2 中心对称(二)(总第四课时)计划上课时间
主备 王宇齐 审阅 审批
一、学习目标:
1、使学生了解中心对称图形的概念,以及两个图形成中心对称和中心对称图形的关系.
2、使学生初步学会识别常见的中心对称图形或图案,并能用推理方式说明一个图形是中心对称图形.
二、重点难点:1、中心对称图形的判断.
2、两个图形成中心对称和中心对称图形的关系,以及中心对称的判定.
三、复习和预习案:C1、阅读教材P65思考回答问题:
(1)线段AB绕它的中点旋转180 后与它本身 。平行四边形ABCD绕两对角线的交点O旋转180 后与它本身 。
(2)把一个图形绕着某个点旋转 ,如果旋转后的图形与原来的图形 ,那么这两个图形叫做 。这个点就是它的 。
B2、中心对称与中心对称图形的区别:中心对称是指 个 图形之间的相互位置关系,成中心对称的 个图形中,其中一个图形上所有点关于对称中心的对称点都在 图形上;而中心对称图形是指 个图形 成中心对称,中心对称图形上所有点关于对称中心的对称点都在 上;中心对称图形的对称中心是图形 的点,而两个图形关于某点成中心对称,对称中心位置 。
B3、中心对称图形与轴对称图形之间的联系:
(1)对称轴条数为 的图形是中心对称图形,对称中心是对称轴的交点;
(2)中心对称图形 是轴对称图形,轴对称图形也 是中心对称图形;
(3)对称轴 的轴对称图形是中心对称图形;
四、讨论与展示、点评、质疑:C1、教材P66第2题完成在书上。
C2、教材P68第2、5、6、8、9题完成在书上。
五、自我检测案:
C1、下列图形中,既是轴对称图形,又是中心对称图形的是( )
A.等边三角形 B.等腰梯形 C.平行四边形 D.正六边形
C2、下列图形中,是中心对称图形,但不是轴对称图形的是( ).
A.正方形 B.矩形 C.菱形 D.平行四边形
C3、下面图形中既是轴对称图形又是中心对称图形的是( )
A.直角 B.等边三角形 C.直角梯形 D.两条相交直线
C4、下列命题中真命题是( )
A.两个等腰三角形一定全等 B.正多边形的每一个内角的度数随边数增多而减少
C.菱形既是中心对称图形,又是轴对称图形 D.两直线平行,同旁内角相等
C5、如图下图所示,平放在正立镜子前的桌面上的数码“21085”在镜子中的像是( )
A.21085 B.28015 C.58012 D.51082
C6、下面的图案中,是中心对称图形的个数有( )个
A.1 B.2 C.3 D.4
B7、如下图,把一张长方形ABCD的纸片,沿EF折叠后,ED′与BC的交点为G,
点D、C分别落在D′、C′的位置上,若∠EFG=55°,则∠1=
B8、如上图将矩形ABCD沿AE折叠,已知∠CED′=60°,则∠AED的大小是
B10、如图,矩形ABCD中,AB=3,BC=4,若将矩形折叠,使C点和A点重合,求折痕EF的长.
2、如图,直线y=2x+2与x轴、y轴分别交于A、B两点,将△AOB绕点O顺时针旋转90°得到△A1OB1.(1)在图中画出△A1OB1;
(2)设过A、A1、B三点的函数解析式为y=ax2+bx+c,求这个解析式.
23.2.3 中心对称(二)(总第五课时)计划上课时间
主备 王宇齐 审阅 审批
一、学习目标:1、掌握在直角坐标系中关于原点对称的点的坐标的关系。
2、运用中心对称的知识导出关于原点对称的点的坐标的性质及其运用它解决实际问题
二、重点难点:关于原点对称的点的坐标的关系及初步应用.
三、复习和预习案:
C1、已知点A和直线L,如图,请画出点A关于L对称的点A′.
C2、如图△ABO,绕点C旋转180°,画出旋转后的图形.
C3、如图,△ABC是正三角形,以点A为中心,把△ADC顺时针旋转60°,画出旋转后的图形.
C4、完成P66探究问题。
C5、两个关于原点对称的点,它们的横坐标 ,纵坐标也 。
两个关于x轴对称的点,它们的横坐标 ,纵坐标 。
两个关于y轴对称的点,它们的横坐标 ,纵坐标 。
C6、已知A(a,2)与B(5,b)关于原点对称,则a= ,b= .
C7、教材P67练习题完成在书上。
四、讨论与展示、点评、质疑:
C1、教材P667例2完成在书上。
C2、作关于原点的中心对称的图形的步骤:(1)写出各点关于原点对称的点的 (2)在坐标平面内 这些对称点的位置。(3) 各点即为所求的对称图形
B3、如图,有一块长方形钢板,工人师傅想把它分成面积相等的两部分,请你用三种方法在图中画出作图痕迹.
五、自我检测案:
B1、下列函数中,图象一定关于原点对称的图象是( )
A.y= B.y=2x+1 C.y=-2x+1 D.以上三种都不可能
C2、如果点P(-3,1),那么点P(-3,1)关于原点的对称点P′的坐标是P′_______.
C3、写出函数y=-与y=具有的一个共同性质______ __(用对称的观点写).
C4、如下图,已知矩形ABCD周长为56cm,O是对称线交点,点O到矩形两条邻边的距离之差等于8cm,则矩形边长中较长的一边等于( )A.8cm B.22cm C.24cm D.11cm
C5、如图,在平面直角坐标系中,A(-3,1),B(-2,3),C(0,2),画出△ABC关于x轴对称的△A′B′C′,再画出△A′B′C′关于y轴对称的△A″B″C″,那么△A″B″C″与△ABC成 对称,理由为: 。
C5、如上图,利用关于原点对称的点的坐标的特点,作出与线段AB关于原点对称的图形.
C6、如图,直线AB与x轴、y轴分别相交于A、B两点,将直线AB绕点O顺时针旋转
90°得到直线A1B1.
(1)在图中画出直线A1B1.
(2)求出经过线段A1B1中点的反比例函数解析式.
23.3 图案设计(总第六课时)计划上课时间
主备 王宇齐 审阅 审批
一、学习目标:
1、通过具体实例认识两个图形中心对称的本质:就是一个图形绕一点旋转180°而成.
2、掌握成中心对称的两个图形的性质,以及利用两种不同方式来作出中心对称的图形.
二、重点难点;中心对称的性质及初步应用;中心对称与旋转之间的关系.
三、复习和预习案:
C1、平移、旋转、轴对称的共同特征是图形变换后的 和 大小不变。
四、讨论与展示、点评、质疑:
C1、阅读教材P71,体会通过旋转、轴对称、平移进行美丽图案设计的流程。
B2、 已知:图A、图B分别是6×6正方形网格上的两个轴对称图形(阴影部分),其面积分别为、(网格中最小的正方形面积为一个平方单位),请观察图形并解答下列问题. (1)填空: 的值是__________; (2)请在图C的网格上画出一个面积为8个平方单位的中心对称图形.
五、自我检测案:
C1.下列这些美丽的图案都是在“几何画板”软件中利用旋转的知识在一个图案的基础上加工而成的,每一个图案都可以看作是它的“基本图案”绕着它的旋转中心旋转得来的,旋转的角度正确的为( )A. B. C. D.
C2.将一张正方形纸片沿如图1所示的虚线剪开后,能拼成下列四个图形,其中是中心对称图形的是( )
C3.某正方形园地是由边长为1的四个小正方形组成的,现要在园地上建一个花坛(阴影部分)使花坛面积是园地面积的一半,以下图中设计不合要求的是( )
B4、用4块如所示的瓷砖拼成一个正方形,使所得正方形(包括色彩因素)分别是具有如下对称性的美术图案:(1)只是轴对称图形而不是中心对称图形;(2)既是轴对称图形又是中心对称图形.画出符合要求的图形各两个.
A5、如图,的∠BAC=120 ,以BC为边向形外作等边,把绕着D点按顺时针方向旋转60 后到的位置。若,求∠BAD的度数和AD的长.
23.3图形的旋转复习(一)(总第七课时)计划上课时间
主备 王宇齐 审阅 审批
一、复习案:
1、旋转:在平面内,把一个图形绕______,按_______旋转______的图形运动,叫做旋转.
2、图形旋转的三个要素:(1)__________; (2)_________;(3)____________.
3、旋转的特征:
(1)图形的________和________都没有发生变化;
(2)_________相等,__________相等;
(3)对应点到旋转中心的距离_________;
(4)图形中的每一点都绕着旋转中心旋转同样大小的_______,对应点与旋转中心连线的夹角是_______.
4、旋转对称图形识别:观察图形是否存在一点,围绕这一点旋转一定角度后能否与图形________.
5、经过两次对称轴相交的轴对称变换,相当于一次______.
6、在成中心对称的两个图形中,连结对称点的线段都经过对称中心,并且被对称中心平分.反过来,如果两个图形的对应点连成的线段都经过某一点,并且被该点_____,那么这两个图形一定关于这一点成中心对称.
二、讨论与展示、点评、质疑:
A1、Rt△ABC与Rt△FED是两块全等的含30o、60o角的三角板,按如图(一)所示拼在一起,CB与DE重合.
(1)求证:四边形ABFC为平行四边形;
(2)取BC中点O,将△ABC绕点O顺时钟方向旋转到如图(二)中△位置,直线与AB、CF分别相交于P、Q两点,猜想OQ、OP长度的大小关系,并证明你的猜想.
(3)在(2)的条件下,指出当旋转角至少为多少度时,四边形PCQB为菱形(不要求证明).
五、自我检测案:
C1、(2009年泸州)如图1,P是正△ABC内的一点,若将△PBC绕点B旋转到△P’BA,
则∠PBP’的度数是( )
A.45° B.60° C.90° D.120°
C2、(2009年陕西省) 如图,∠AOB=90°,∠B=30°,△A’OB’可以看作是由△AOB绕点O顺时针旋转α角度得到的,若点A’在AB上,则旋转角α的大小可以是 ( )
A.30° B.45° C.60° D.90°
C3、(2009年桂林市、百色市)如图所示,在方格纸上建立的平面直角坐标系中,将△ABO绕点O按顺时针方向旋转90°,得 ,则点的坐标为 ( ).
A.(3,1) B.(3,2) C.(2,3) D.(1,3)
C4、如图9所示,每个小方格都是边长为1的正方形,以O点为坐标原点建立平面直角坐标系.(1)画出四边形OABC关于y轴对称的四边形OA1B1C1,并写出点B1的坐标是 .
(2)画出四边形OABC绕点O顺时针方向旋转90°后得到的四边形OA2B2C2.
A5、如图,在Rt△ABC中,∠ACB=90°, ∠B =60°,BC=2.点0是AC的中点,过点0的直线l从与AC重合的位置开始,绕点0作逆时针旋转,交AB边于点D.过点C作CE∥AB交直线l于点E,设直线l的旋转角为α.
(1) ①当α=________度时,四边形EDBC是等腰梯形,此时AD的长为_________;
②当α=________度时,四边形EDBC是直角梯形,此时AD的长为_________;
(2)当α=90°时,判断四边形EDBC是否为菱形,并说明理由.
23.3图形的旋转复习(二)(总第八课时)计划上课时间
主备 王宇齐 审阅 审批
一、讨论与展示、点评、质疑:
C1、(2009年潍坊)在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,的三个顶点都在格点上(每个小方格的顶点叫格点).画出绕点O逆时针旋转90°后的.
B2、如图,在中,,,将绕点沿逆时针方向旋转得到.
(1)线段的长是 ,的度数是 ;
(2)连结,求证:四边形是平行四边形;
(3)求四边形的面积.
A3、如图①,在Rt△ABC中,∠BAC=90°,AB=AC=,D、E两点分别在AC、BC上,且DE∥AB,CD=.将△CDE绕点C顺时针旋转,得到△CD'E'(如图②,点D'、E'分别与点D、E对应),点E'在AB上,D'E'与AC相交于点M.
(1)求∠ACE’的度数;
(2)求证:四边形ABCD'是梯形;
(3)求△AD'M的面积.
五、自我检测案:
C1、下列图形中,既是轴对称图形,又是中心对称图形的是( )
A.等腰梯形 B.平行四边形 C.正三角形 D.矩形
5、单词NAME的四个字母中,是中心对称图形的是( )
A.N B.A C.M D.E
C2、某校计划修建一座既是中心对称图形又是轴对称图形的花坛,从学生中征集到的设计方案有等腰三角形、正三角形、等腰梯形、菱形等四种方案,你认为符合条件的是( )
A.等腰三角形 B.正三角形 C.等腰梯形 D.菱形
C3、(2009年锦州)下列图形中,既是轴对称图形,又是中心对称图形的是 ( )
A B C D
C4、已知如图1所示的四张牌,若将其中一张牌旋转180O后得到图2,则旋转的牌是( )
C5、(2009成都)在平面直角坐标系xOy中,已知点A(2,3),若将OA绕原点O逆时针旋转180°得到0A′,则点A′在平面直角坐标系中的位置是在( )
(A)第一象限 (B)第二象限 (c)第三象限 (D)第四象限
C6、已知点的坐标为,为坐标原点,连结,将线段绕点按逆时针方向旋转90°得,则点的坐标为( ).
A. B. C. D.
C7、如图,点A,B,C的坐标分别为.从下面四个点,,,中选择一个点,以A,B,C与该点为顶点的四边形不是中心对称图形,则该点是 ( )
A.M B.N C.P D.Q
23.3图形的旋转复习(三)(总第九课时)计划上课时间
主备 王宇齐 审阅 审批
一、讨论与展示、点评、质疑:
C1、(2009年长春)图①、图②均为的正方形网格,点在格点上.
(1)在图①中确定格点,并画出以为顶点的四边形,使其为轴对称图形.(画一个即可)(3分)
(2)在图②中确定格点,并画出以为顶点的四边形,使其为中心对称图形.(画一个即可)(3分)
A2、如图1,已知矩形ABED,点C是边DE的中点,且AB = 2AD.
(1)判断△ABC的形状,并说明理由;
(2)保持图1中ABC固定不变,绕点C旋转DE所在的直线MN到图2中(当垂线段AD、BE在直线MN的同侧),试探究线段AD、BE、DE长度之间有什么关系?并给予证明;
(3)保持图2中△ABC固定不变,继续绕点C旋转DE所在的直线MN到图3中的位置(当垂线段AD、BE在直线MN的异侧).试探究线段AD、BE、DE长度之间有什么关系?并给予证明.
五、自我检测案:
C1、(2009肇庆)在平面直角坐标系中,点关于原点对称点的坐标是 .
C2、(2009年湖北十堰市)如图,在平面直角坐标系中,点A的坐标为(1,4),将线段OA绕点O顺时针旋转90°得到线段OA′,则点A′的坐标是 .
B3、(2009年淄博市)如图,四边形EFGH是由四边形经过旋转得到的.如果用有序数对(2,1)表示方格纸上A点的位置,用(1,2)表示B点的位置,那么四边形旋转得到四边形EFGH时的旋转中心用有序数对表示是 .
C4、如图2 所示,五角星的顶点是一个正五边形的五个顶点.这个五角星可以由一个基本图形(图中的阴影部分)绕中心O至少经过_____次旋转而得到, 每一次旋转_____度.
C5、点A的坐标为(,0),把点A绕着坐标原点顺时针旋转135 到点B,那么点B的坐标是 _________ .
C6、如图,直线与轴、轴分别交于、两点,把绕点A顺时针旋转90°后得到,则点的坐标是 .
B7、如图所示,在平面直角坐标系中,三个顶点的坐标是.将绕原点按逆时针方向旋转后得到,则点的坐标是 .
A8、在平面直角坐标系中,已知3个点的坐标分别为、、. 一只电子蛙位于坐标原点处,第1次电子蛙由原点跳到以为对称中心的对称点,第2次电子蛙由点跳到以为对称中心的对称点,第3次电子蛙由点跳到以为对称中心的对称点,…,按此规律,电子蛙分别以、、为对称中心继续跳下去.问当电子蛙跳了2009次后,电子蛙落点的坐标是(__ , __).
B
A
C
1
2
4
3
0
-1
-2
-3
1
2
3
A
B
A
图①
B
C
M
D
E
A
B
C
D’
E’
图②
图1
图2
A.
B.
C.
D.
A
B
C
图①
A
B
C
图②
图1
图2
图3
图2
O
A
B
O
Ob
Bb
Ab
yb
A1
B1
x
主备 王宇齐 审阅 审批
一、学习目标:
1、通过具体实例认识图形的旋转,理解“对应点到旋转中心的距离相等”以及“旋转前、后的图形全等”的基本性质。
二、学习重点:对生活中的旋转现象作数学上的分析,理解旋转的定义。
学习难点:对旋转现象进行分析研究,旋转后的现象进行探索。
三、复习和预习案:
C1、 如下图,把一个平面图形绕着平面内某一点O转动一个角度的图形变换叫做 .点O叫做 ,转动的角叫做 .
C2、 一般地,可以根据定义得出旋转的以下性质:(1)对应点到旋转中心的距离 .
(2)对应点与旋转中心所连线段的夹角等于 .(3)旋转前、后的图形 .
四、讨论与展示、点评、质疑:
C1、如上图所示,AC是正方形ABCD的对角线,△ABC经过旋转后到达△AEF的位置,则旋转中心是 ,旋转方向是 ,旋转角度是 度,点B的对应点是 。
C2、选择题:(1)如上图所示,在平面直角坐标系中,点A、B的坐标分别为(-2,0)和(2,0).月牙①绕点B顺时针旋转90°得到月牙②,则点A的对应点A’的坐标为( )
A.(2,2) B.(2,4) C.(4,2) D.(1,2)
(2)下列各组图中,图形甲变成图形乙,既能用平移,又能用旋转的是( )
C3、教材P56练习第2、3题。(过程完成有书上)
五、自我检测案:
C1、 下面生活中的实例,不是旋转的是( )
A. 传送带传送货物 B. 螺旋桨的运动 C. 风车风轮的运动 D. 自行车车轮的运动
C2、 中国国旗上有五个五角星,其中四个小五角星可以看作是其中一个旋转得到的,旋转中心是( )
A. 最上面的小五角星中心 B. 最下面的小五角星中心
C. 大五角星中心 D. 长方形左上角的顶点
C3、如上图,将△ABC绕点A逆时针旋转80°得到△AB′C′.若∠BAC=50°,
则∠CAB′的度数为( )
A. 30° B. 40° C. 50° D. 80°
C4、将一个三角形旋转,旋转中心应选在( )
A. 三角形的顶点 B. 三角形的外部
C. 三角形的三条边上 D. 平面内的任意位置
C5、将叶片图案旋转180°后,得到的图形是( )
B6、数学课上,老师让同学们观察如上图所示的图形,问:它绕着圆心O旋转多少度后和它自身重合?甲同学说:45°;乙同学说:60°;丙同学说:90°;丁同学说:135°.以上四位同学的回答中,错误的是( )
A. 甲 B. 乙 C. 丙 D. 丁
C7、如果4张扑克按图1的形式摆放在桌面上,将其中一张旋转180°后,扑克的放置情况如图2所示,那么旋转的扑克从左起是( )
A. 第一张 B. 第二张 C. 第三张 D. 第四张
C8、如图所示,请你先观察(1)~(3),然后确定第四张为( )
A. B. C. D.
23.1 图形的旋转(2)(总第二课时)计划上课时间
主备 王宇齐 审阅 审批
一、学习目标:
1、理解图形旋转的特征,并能初步地加以应用;掌握图形旋转的基本作图。
2、通过感受图形的旋转,使学生进一步深入理解旋转的性质,从而培养学生分析、解决实际问题的能力。
二、学习重点难点:图形旋转的性质的初步应用。
三、复习和预习案:
C1.在平面内,把一个图形绕着某______沿着某个方向转动______的图形变换叫做旋转.这个点O叫做_____,转动的角叫做_____.因此,图形的旋转是由____ _, 以及______决定的.
C2.如果图形上的点P经过旋转变为点P′,那么这两点叫做这个旋转的______.
C3.如图,△AOB旋转到△A′OB′的位置.若∠AOA′=90°,则旋转中心是点______.旋转角是______.点A的对应点是______.线段AB的对应线段是______.∠B的对应角是______.∠BOB′=______度。
3题图 4题图
C4.如图,△ABC绕着点O旋转到△DEF的位置,则旋转中心是______.旋转角是______.AO=______,AB=______,∠ACB=∠______.
四、讨论与展示、点评、质疑:
C1、阅读教材P58--59回答问题:(1)教材中图23. 1—7是把一个图案进行 ,其中 不变,改变了 而设计的图案。教材中图23. 1—8是把一个图案进行 ,其中 不变,改变了 而设计的图案。
(2)利用旋转设计图案时,基本图形唯一吗? 。
旋转角的度数唯一吗? 。旋转中心唯一吗? 。
观察图23.1-9可知,经过旋转可以设计美丽的图案。
C2、教材P57例:(图画在右边空白处)
解:
C3、教材P58第2题:解:
C4、教材P60第4、5题完成在书上。
C5、教材P61第10题:
解:
五、自我检测案:
C1.图形之间的变换关系包括 、_______、 以及它们的组合变换.
C2.如下右图,过圆心O和图上一点A连一条曲线,将OA绕O点按同一方向连续旋转三次,每次旋转90°,把圆分成四部分,这四部分面积是圆的_________.
C3.已知:如图,F是正方形ABCD中BC边上一点,延长AB到E,使得BE=BF,试用旋转的性质说明:AF=CE且AF⊥CE.
C4、 如图所示,△ABC中,∠ACB=90°,∠BAC=30°,点D是斜边上任意一点,以A点为中心,把△ACD顺时针旋转30°,画出旋转后的图形.
C5、教材P60第7题:解:五角星的旋转角度是 或 或 或 度,在三角形的旋转角度是 或 度。
C6、教材P61第9题:解:利用等腰三角形旋转制作五角星的方法是先确定旋转为 ,旋转角度为 度,经过 次旋转可以制作而成。
C7.一个平行四边形ABCD,如果绕其对角线的交点O旋转,至少要旋转______度,才可与其自身重合.
B8.钟表的运动可以看作是一种旋转现象,那么分针匀速旋转时,它的旋转中心是钟表的旋转轴的轴心,经过45分钟分针旋转了______度.
B9. 由8时15分到8时40分,时钟的分针旋转的角度为________度,时针旋转的角度为__________度。时间和分针的夹角是 度。
B10、9点20分时针和分针的夹角是 度。
23.2.1 中心对称(一)(总第三课时)计划上课时间
主备 王宇齐 审阅 审批
一、学习目标:两个图形关于某一点对称或中心对称就是一个图形绕一点旋转180°而成。
2、掌握成中心对称的两个图形的性质,以及利用两种不同方式来作出中心对称的图形.
二、学习重点难点:中心对称的性质及初步应用.
三、复习和预习案:
C1. 图形的旋转是由_________和_________所决定的,旋转不改变图形的_____和_____.
C2. 如下图(2)可以看作是由图(1)经过______次旋转,每次旋转______度得到的.
(1) (2) (3)
C3、如上第三个图所示,某战士在训练场上练习射击,发现子弹均击中靶子上的阴影部分,那么阴影部分的面积是圆的面积的 。
C4、观察与实验:如上(1((2)(3)图,用透明纸覆盖在图上,描出其中的一部分,用大头针固定在O处。旋转180°后,你有什么发现?
发现:把一个图形绕着某一个 旋转 ,如果他们能够与另一个图形 ,那么就说这 个图形 或 ,这个点叫做 ,这两个图形中的 叫做关于中心的 .
C5、中心对称性质:(1)
(2)
四、讨论与展示、点评、质疑:
阅读教材P64例1完成下列各题:
C1、教材P64第1、2题完成在书上。
C2、教材P67第1、题完成在书上。
C3、教材P68第7题完成在书上。
五、自我检测案:
C1、已知下列命题:① 关于中心对称的两个图形一定不全等; ②关于中心对称的两个图形一定全等; ③两个全等的图形一定成中心对称,其中真命题的个数是( )
A、0 B、1 C、2 D、3
C2、下列图形即是轴对称又是中心对称的是( )
A B C C
C3、已知,△ABC与△DEF成中心对称,请找出它们的对称中心。
C4、如图,若四边形ABCD与四边形CEFG成中心对称,则它们的对称中心是______,点A的对称点是______,E的对称点是______.BD∥______且BD=______.连结A,F的线段经过______,且被C点______,△ABD≌______.
C5、如上图,点A'是A关于点O的对称点,请作出线段AB关于点O对称的线段A'B'
C6、如上图,在△ABC中,∠B=90°,∠C=30°,AB=1 ,将△ABC绕定点A旋转180°,点C落在C'处,则CC'= 。
B7、如图,已知AD是△ABC的中线:
(1)画出与△ACD关于D点成中心对称的三角形;(2)与AC相等的线段是 。
(3)若AB=5、AC=3,则线段AD的取值范围是 。
23.2.2 中心对称(二)(总第四课时)计划上课时间
主备 王宇齐 审阅 审批
一、学习目标:
1、使学生了解中心对称图形的概念,以及两个图形成中心对称和中心对称图形的关系.
2、使学生初步学会识别常见的中心对称图形或图案,并能用推理方式说明一个图形是中心对称图形.
二、重点难点:1、中心对称图形的判断.
2、两个图形成中心对称和中心对称图形的关系,以及中心对称的判定.
三、复习和预习案:C1、阅读教材P65思考回答问题:
(1)线段AB绕它的中点旋转180 后与它本身 。平行四边形ABCD绕两对角线的交点O旋转180 后与它本身 。
(2)把一个图形绕着某个点旋转 ,如果旋转后的图形与原来的图形 ,那么这两个图形叫做 。这个点就是它的 。
B2、中心对称与中心对称图形的区别:中心对称是指 个 图形之间的相互位置关系,成中心对称的 个图形中,其中一个图形上所有点关于对称中心的对称点都在 图形上;而中心对称图形是指 个图形 成中心对称,中心对称图形上所有点关于对称中心的对称点都在 上;中心对称图形的对称中心是图形 的点,而两个图形关于某点成中心对称,对称中心位置 。
B3、中心对称图形与轴对称图形之间的联系:
(1)对称轴条数为 的图形是中心对称图形,对称中心是对称轴的交点;
(2)中心对称图形 是轴对称图形,轴对称图形也 是中心对称图形;
(3)对称轴 的轴对称图形是中心对称图形;
四、讨论与展示、点评、质疑:C1、教材P66第2题完成在书上。
C2、教材P68第2、5、6、8、9题完成在书上。
五、自我检测案:
C1、下列图形中,既是轴对称图形,又是中心对称图形的是( )
A.等边三角形 B.等腰梯形 C.平行四边形 D.正六边形
C2、下列图形中,是中心对称图形,但不是轴对称图形的是( ).
A.正方形 B.矩形 C.菱形 D.平行四边形
C3、下面图形中既是轴对称图形又是中心对称图形的是( )
A.直角 B.等边三角形 C.直角梯形 D.两条相交直线
C4、下列命题中真命题是( )
A.两个等腰三角形一定全等 B.正多边形的每一个内角的度数随边数增多而减少
C.菱形既是中心对称图形,又是轴对称图形 D.两直线平行,同旁内角相等
C5、如图下图所示,平放在正立镜子前的桌面上的数码“21085”在镜子中的像是( )
A.21085 B.28015 C.58012 D.51082
C6、下面的图案中,是中心对称图形的个数有( )个
A.1 B.2 C.3 D.4
B7、如下图,把一张长方形ABCD的纸片,沿EF折叠后,ED′与BC的交点为G,
点D、C分别落在D′、C′的位置上,若∠EFG=55°,则∠1=
B8、如上图将矩形ABCD沿AE折叠,已知∠CED′=60°,则∠AED的大小是
B10、如图,矩形ABCD中,AB=3,BC=4,若将矩形折叠,使C点和A点重合,求折痕EF的长.
2、如图,直线y=2x+2与x轴、y轴分别交于A、B两点,将△AOB绕点O顺时针旋转90°得到△A1OB1.(1)在图中画出△A1OB1;
(2)设过A、A1、B三点的函数解析式为y=ax2+bx+c,求这个解析式.
23.2.3 中心对称(二)(总第五课时)计划上课时间
主备 王宇齐 审阅 审批
一、学习目标:1、掌握在直角坐标系中关于原点对称的点的坐标的关系。
2、运用中心对称的知识导出关于原点对称的点的坐标的性质及其运用它解决实际问题
二、重点难点:关于原点对称的点的坐标的关系及初步应用.
三、复习和预习案:
C1、已知点A和直线L,如图,请画出点A关于L对称的点A′.
C2、如图△ABO,绕点C旋转180°,画出旋转后的图形.
C3、如图,△ABC是正三角形,以点A为中心,把△ADC顺时针旋转60°,画出旋转后的图形.
C4、完成P66探究问题。
C5、两个关于原点对称的点,它们的横坐标 ,纵坐标也 。
两个关于x轴对称的点,它们的横坐标 ,纵坐标 。
两个关于y轴对称的点,它们的横坐标 ,纵坐标 。
C6、已知A(a,2)与B(5,b)关于原点对称,则a= ,b= .
C7、教材P67练习题完成在书上。
四、讨论与展示、点评、质疑:
C1、教材P667例2完成在书上。
C2、作关于原点的中心对称的图形的步骤:(1)写出各点关于原点对称的点的 (2)在坐标平面内 这些对称点的位置。(3) 各点即为所求的对称图形
B3、如图,有一块长方形钢板,工人师傅想把它分成面积相等的两部分,请你用三种方法在图中画出作图痕迹.
五、自我检测案:
B1、下列函数中,图象一定关于原点对称的图象是( )
A.y= B.y=2x+1 C.y=-2x+1 D.以上三种都不可能
C2、如果点P(-3,1),那么点P(-3,1)关于原点的对称点P′的坐标是P′_______.
C3、写出函数y=-与y=具有的一个共同性质______ __(用对称的观点写).
C4、如下图,已知矩形ABCD周长为56cm,O是对称线交点,点O到矩形两条邻边的距离之差等于8cm,则矩形边长中较长的一边等于( )A.8cm B.22cm C.24cm D.11cm
C5、如图,在平面直角坐标系中,A(-3,1),B(-2,3),C(0,2),画出△ABC关于x轴对称的△A′B′C′,再画出△A′B′C′关于y轴对称的△A″B″C″,那么△A″B″C″与△ABC成 对称,理由为: 。
C5、如上图,利用关于原点对称的点的坐标的特点,作出与线段AB关于原点对称的图形.
C6、如图,直线AB与x轴、y轴分别相交于A、B两点,将直线AB绕点O顺时针旋转
90°得到直线A1B1.
(1)在图中画出直线A1B1.
(2)求出经过线段A1B1中点的反比例函数解析式.
23.3 图案设计(总第六课时)计划上课时间
主备 王宇齐 审阅 审批
一、学习目标:
1、通过具体实例认识两个图形中心对称的本质:就是一个图形绕一点旋转180°而成.
2、掌握成中心对称的两个图形的性质,以及利用两种不同方式来作出中心对称的图形.
二、重点难点;中心对称的性质及初步应用;中心对称与旋转之间的关系.
三、复习和预习案:
C1、平移、旋转、轴对称的共同特征是图形变换后的 和 大小不变。
四、讨论与展示、点评、质疑:
C1、阅读教材P71,体会通过旋转、轴对称、平移进行美丽图案设计的流程。
B2、 已知:图A、图B分别是6×6正方形网格上的两个轴对称图形(阴影部分),其面积分别为、(网格中最小的正方形面积为一个平方单位),请观察图形并解答下列问题. (1)填空: 的值是__________; (2)请在图C的网格上画出一个面积为8个平方单位的中心对称图形.
五、自我检测案:
C1.下列这些美丽的图案都是在“几何画板”软件中利用旋转的知识在一个图案的基础上加工而成的,每一个图案都可以看作是它的“基本图案”绕着它的旋转中心旋转得来的,旋转的角度正确的为( )A. B. C. D.
C2.将一张正方形纸片沿如图1所示的虚线剪开后,能拼成下列四个图形,其中是中心对称图形的是( )
C3.某正方形园地是由边长为1的四个小正方形组成的,现要在园地上建一个花坛(阴影部分)使花坛面积是园地面积的一半,以下图中设计不合要求的是( )
B4、用4块如所示的瓷砖拼成一个正方形,使所得正方形(包括色彩因素)分别是具有如下对称性的美术图案:(1)只是轴对称图形而不是中心对称图形;(2)既是轴对称图形又是中心对称图形.画出符合要求的图形各两个.
A5、如图,的∠BAC=120 ,以BC为边向形外作等边,把绕着D点按顺时针方向旋转60 后到的位置。若,求∠BAD的度数和AD的长.
23.3图形的旋转复习(一)(总第七课时)计划上课时间
主备 王宇齐 审阅 审批
一、复习案:
1、旋转:在平面内,把一个图形绕______,按_______旋转______的图形运动,叫做旋转.
2、图形旋转的三个要素:(1)__________; (2)_________;(3)____________.
3、旋转的特征:
(1)图形的________和________都没有发生变化;
(2)_________相等,__________相等;
(3)对应点到旋转中心的距离_________;
(4)图形中的每一点都绕着旋转中心旋转同样大小的_______,对应点与旋转中心连线的夹角是_______.
4、旋转对称图形识别:观察图形是否存在一点,围绕这一点旋转一定角度后能否与图形________.
5、经过两次对称轴相交的轴对称变换,相当于一次______.
6、在成中心对称的两个图形中,连结对称点的线段都经过对称中心,并且被对称中心平分.反过来,如果两个图形的对应点连成的线段都经过某一点,并且被该点_____,那么这两个图形一定关于这一点成中心对称.
二、讨论与展示、点评、质疑:
A1、Rt△ABC与Rt△FED是两块全等的含30o、60o角的三角板,按如图(一)所示拼在一起,CB与DE重合.
(1)求证:四边形ABFC为平行四边形;
(2)取BC中点O,将△ABC绕点O顺时钟方向旋转到如图(二)中△位置,直线与AB、CF分别相交于P、Q两点,猜想OQ、OP长度的大小关系,并证明你的猜想.
(3)在(2)的条件下,指出当旋转角至少为多少度时,四边形PCQB为菱形(不要求证明).
五、自我检测案:
C1、(2009年泸州)如图1,P是正△ABC内的一点,若将△PBC绕点B旋转到△P’BA,
则∠PBP’的度数是( )
A.45° B.60° C.90° D.120°
C2、(2009年陕西省) 如图,∠AOB=90°,∠B=30°,△A’OB’可以看作是由△AOB绕点O顺时针旋转α角度得到的,若点A’在AB上,则旋转角α的大小可以是 ( )
A.30° B.45° C.60° D.90°
C3、(2009年桂林市、百色市)如图所示,在方格纸上建立的平面直角坐标系中,将△ABO绕点O按顺时针方向旋转90°,得 ,则点的坐标为 ( ).
A.(3,1) B.(3,2) C.(2,3) D.(1,3)
C4、如图9所示,每个小方格都是边长为1的正方形,以O点为坐标原点建立平面直角坐标系.(1)画出四边形OABC关于y轴对称的四边形OA1B1C1,并写出点B1的坐标是 .
(2)画出四边形OABC绕点O顺时针方向旋转90°后得到的四边形OA2B2C2.
A5、如图,在Rt△ABC中,∠ACB=90°, ∠B =60°,BC=2.点0是AC的中点,过点0的直线l从与AC重合的位置开始,绕点0作逆时针旋转,交AB边于点D.过点C作CE∥AB交直线l于点E,设直线l的旋转角为α.
(1) ①当α=________度时,四边形EDBC是等腰梯形,此时AD的长为_________;
②当α=________度时,四边形EDBC是直角梯形,此时AD的长为_________;
(2)当α=90°时,判断四边形EDBC是否为菱形,并说明理由.
23.3图形的旋转复习(二)(总第八课时)计划上课时间
主备 王宇齐 审阅 审批
一、讨论与展示、点评、质疑:
C1、(2009年潍坊)在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,的三个顶点都在格点上(每个小方格的顶点叫格点).画出绕点O逆时针旋转90°后的.
B2、如图,在中,,,将绕点沿逆时针方向旋转得到.
(1)线段的长是 ,的度数是 ;
(2)连结,求证:四边形是平行四边形;
(3)求四边形的面积.
A3、如图①,在Rt△ABC中,∠BAC=90°,AB=AC=,D、E两点分别在AC、BC上,且DE∥AB,CD=.将△CDE绕点C顺时针旋转,得到△CD'E'(如图②,点D'、E'分别与点D、E对应),点E'在AB上,D'E'与AC相交于点M.
(1)求∠ACE’的度数;
(2)求证:四边形ABCD'是梯形;
(3)求△AD'M的面积.
五、自我检测案:
C1、下列图形中,既是轴对称图形,又是中心对称图形的是( )
A.等腰梯形 B.平行四边形 C.正三角形 D.矩形
5、单词NAME的四个字母中,是中心对称图形的是( )
A.N B.A C.M D.E
C2、某校计划修建一座既是中心对称图形又是轴对称图形的花坛,从学生中征集到的设计方案有等腰三角形、正三角形、等腰梯形、菱形等四种方案,你认为符合条件的是( )
A.等腰三角形 B.正三角形 C.等腰梯形 D.菱形
C3、(2009年锦州)下列图形中,既是轴对称图形,又是中心对称图形的是 ( )
A B C D
C4、已知如图1所示的四张牌,若将其中一张牌旋转180O后得到图2,则旋转的牌是( )
C5、(2009成都)在平面直角坐标系xOy中,已知点A(2,3),若将OA绕原点O逆时针旋转180°得到0A′,则点A′在平面直角坐标系中的位置是在( )
(A)第一象限 (B)第二象限 (c)第三象限 (D)第四象限
C6、已知点的坐标为,为坐标原点,连结,将线段绕点按逆时针方向旋转90°得,则点的坐标为( ).
A. B. C. D.
C7、如图,点A,B,C的坐标分别为.从下面四个点,,,中选择一个点,以A,B,C与该点为顶点的四边形不是中心对称图形,则该点是 ( )
A.M B.N C.P D.Q
23.3图形的旋转复习(三)(总第九课时)计划上课时间
主备 王宇齐 审阅 审批
一、讨论与展示、点评、质疑:
C1、(2009年长春)图①、图②均为的正方形网格,点在格点上.
(1)在图①中确定格点,并画出以为顶点的四边形,使其为轴对称图形.(画一个即可)(3分)
(2)在图②中确定格点,并画出以为顶点的四边形,使其为中心对称图形.(画一个即可)(3分)
A2、如图1,已知矩形ABED,点C是边DE的中点,且AB = 2AD.
(1)判断△ABC的形状,并说明理由;
(2)保持图1中ABC固定不变,绕点C旋转DE所在的直线MN到图2中(当垂线段AD、BE在直线MN的同侧),试探究线段AD、BE、DE长度之间有什么关系?并给予证明;
(3)保持图2中△ABC固定不变,继续绕点C旋转DE所在的直线MN到图3中的位置(当垂线段AD、BE在直线MN的异侧).试探究线段AD、BE、DE长度之间有什么关系?并给予证明.
五、自我检测案:
C1、(2009肇庆)在平面直角坐标系中,点关于原点对称点的坐标是 .
C2、(2009年湖北十堰市)如图,在平面直角坐标系中,点A的坐标为(1,4),将线段OA绕点O顺时针旋转90°得到线段OA′,则点A′的坐标是 .
B3、(2009年淄博市)如图,四边形EFGH是由四边形经过旋转得到的.如果用有序数对(2,1)表示方格纸上A点的位置,用(1,2)表示B点的位置,那么四边形旋转得到四边形EFGH时的旋转中心用有序数对表示是 .
C4、如图2 所示,五角星的顶点是一个正五边形的五个顶点.这个五角星可以由一个基本图形(图中的阴影部分)绕中心O至少经过_____次旋转而得到, 每一次旋转_____度.
C5、点A的坐标为(,0),把点A绕着坐标原点顺时针旋转135 到点B,那么点B的坐标是 _________ .
C6、如图,直线与轴、轴分别交于、两点,把绕点A顺时针旋转90°后得到,则点的坐标是 .
B7、如图所示,在平面直角坐标系中,三个顶点的坐标是.将绕原点按逆时针方向旋转后得到,则点的坐标是 .
A8、在平面直角坐标系中,已知3个点的坐标分别为、、. 一只电子蛙位于坐标原点处,第1次电子蛙由原点跳到以为对称中心的对称点,第2次电子蛙由点跳到以为对称中心的对称点,第3次电子蛙由点跳到以为对称中心的对称点,…,按此规律,电子蛙分别以、、为对称中心继续跳下去.问当电子蛙跳了2009次后,电子蛙落点的坐标是(__ , __).
B
A
C
1
2
4
3
0
-1
-2
-3
1
2
3
A
B
A
图①
B
C
M
D
E
A
B
C
D’
E’
图②
图1
图2
A.
B.
C.
D.
A
B
C
图①
A
B
C
图②
图1
图2
图3
图2
O
A
B
O
Ob
Bb
Ab
yb
A1
B1
x
同课章节目录
