3.4.1 圆周角与圆心角的关系 课件(共21张PPT)
文档属性
| 名称 | 3.4.1 圆周角与圆心角的关系 课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 57.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-15 00:00:00 | ||
图片预览



文档简介
(共21张PPT)
北师版九年级下册 圆
§3.4.1 圆周角与圆心角的关系
1、理解圆周角的概念.
2、掌握圆周角的两个特征、定理和推论一的内容及简单应用.
3、继续培养学生观察、分析、想象、归纳和逻辑推理的能力.
4、渗透由“特殊到一般”,由“一般到特殊”的数学思想方法.
情境导入
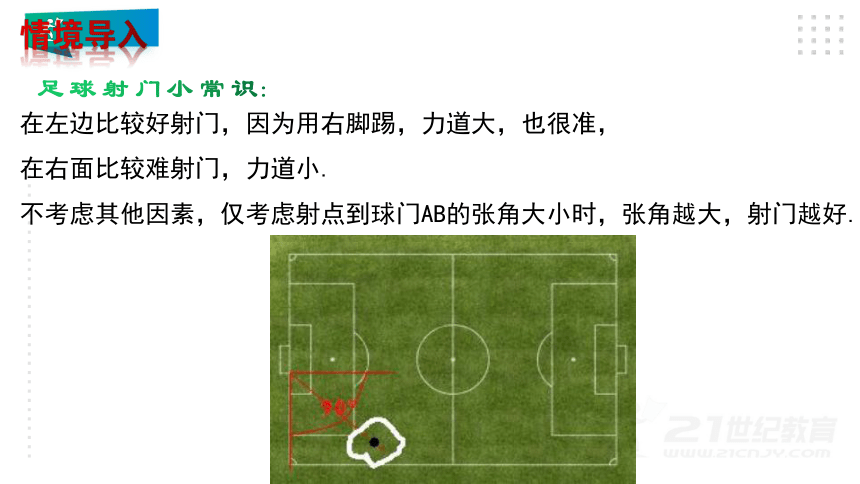
足球射门小常识:
在左边比较好射门,因为用右脚踢,力道大,也很准,
在右面比较难射门,力道小.
不考虑其他因素,仅考虑射点到球门AB的张角大小时,张角越大,射门越好.
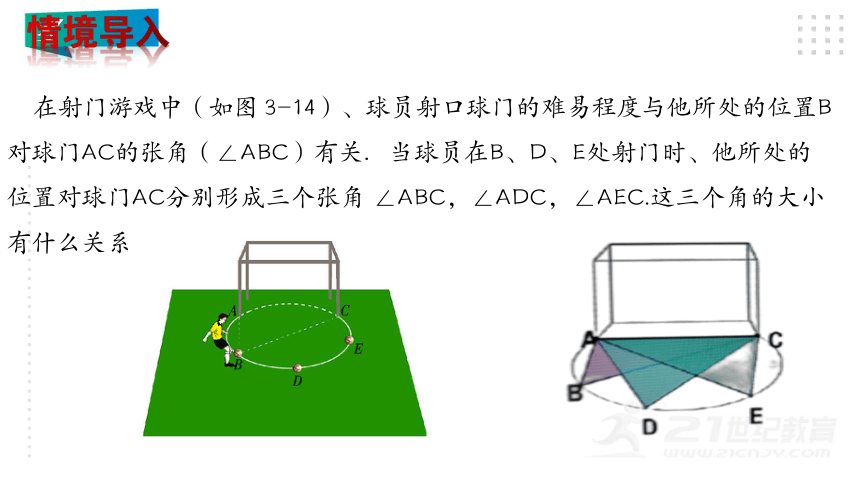
在射门游戏中(如图 3-14)、球员射口球门的难易程度与他所处的位置B
对球门AC的张角(∠ABC)有关.当球员在B、D、E处射门时、他所处的
位置对球门AC分别形成三个张角 ∠ABC,∠ADC,∠AEC.这三个角的大小
有什么关系
情境导入
新知讲解
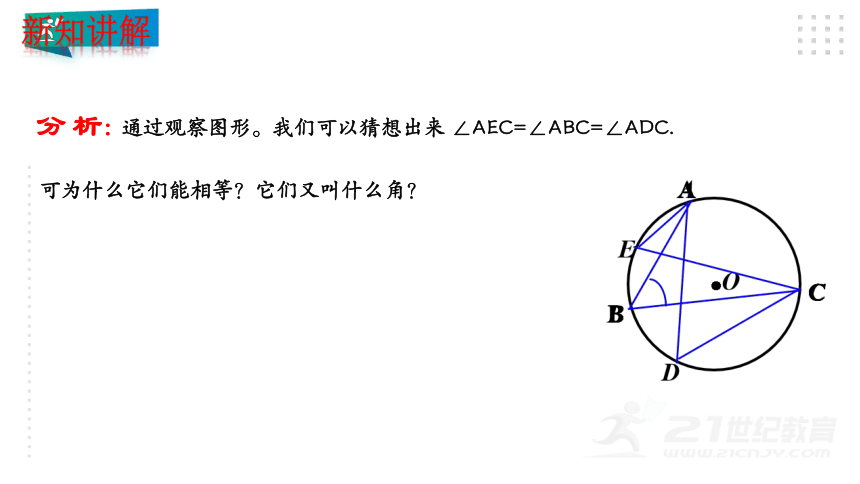
分析: 通过观察图形。我们可以猜想出来 ∠AEC=∠ABC=∠ADC.
可为什么它们能相等?它们又叫什么角?
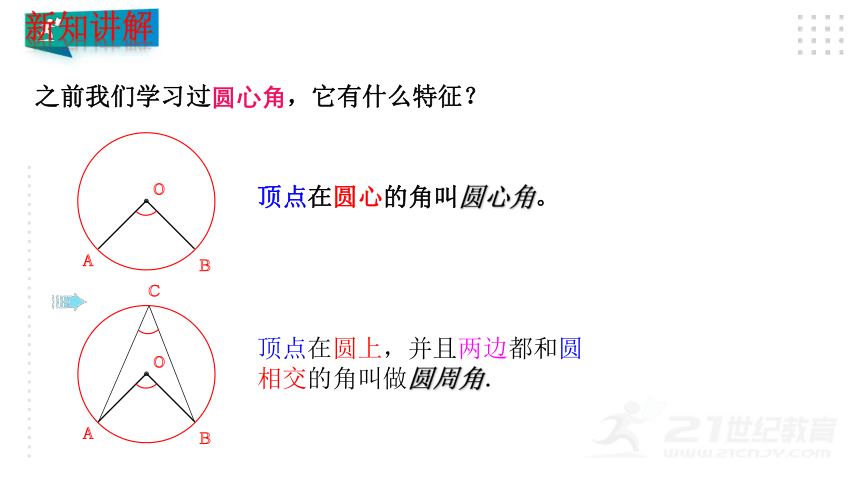
之前我们学习过圆心角,它有什么特征?
新知讲解
o
A
B
顶点在圆心的角叫圆心角。
o
A
B
C
顶点在圆上,并且两边都和圆相交的角叫做圆周角.
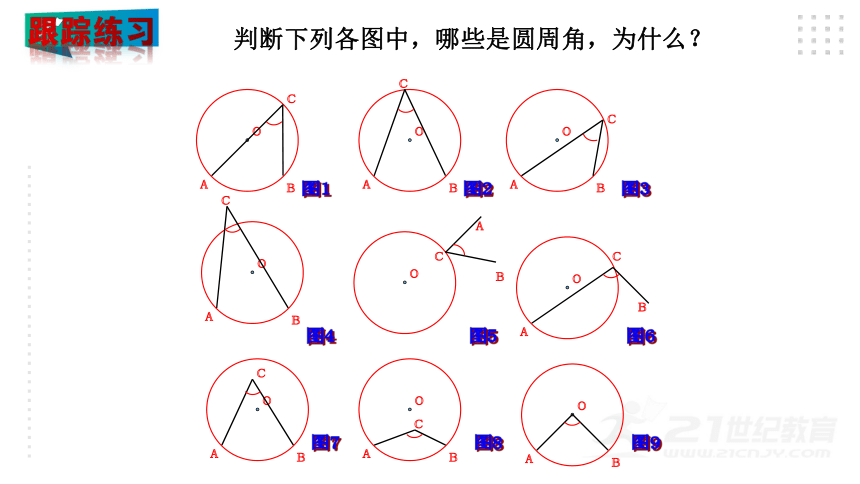
判断下列各图中,哪些是圆周角,为什么?
o
A
B
o
A
B
o
A
B
o
A
B
o
A
B
o
A
B
o
A
B
o
A
B
o
A
B
C
C
C
C
C
C
C
C
图1
图2
图3
图4
图5
图6
图7
图8
图9
跟踪练习
圆周角.GSP
如图,观察变动点D在圆周上的位置,圆周角的度数有没有变化?你能发现什么规律吗?
再分别量出图中弧AB所对的圆心角的度数,比较一下两个角的度数大小关系,你什么发现?
新知讲解
同弧所对的圆周角的度数没有变化,并且它的度数恰好等于这条弧所对的圆心角的度数的一半.
同弧所对圆周角与圆心角的关系
合作探究
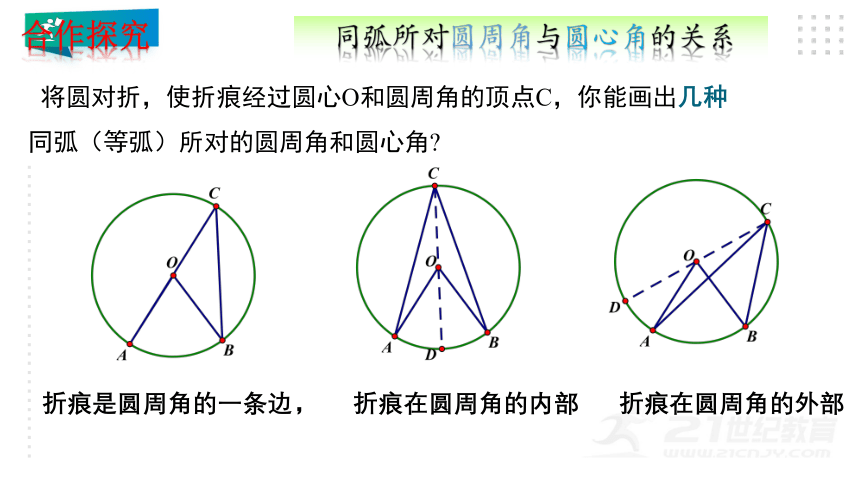
将圆对折,使折痕经过圆心O和圆周角的顶点C,你能画出几种同弧(等弧)所对的圆周角和圆心角
折痕是圆周角的一条边,
折痕在圆周角的内部
折痕在圆周角的外部
(1)在圆周角的一条边上;
即
∵OC=OB,
∴∠OBC=∠C.
又∠BOA=∠OBC+∠C
∴∠BOA=2∠C
(2)在圆周角的内部.
圆心O在∠BAC的内部,作直径AD,利用(1)的结果,有
(3)在圆周角的外部.
圆心O在∠BAC的外部,作直径AD,利用(1)的结果,有
在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
圆周角定理
新知讲解
·
A
B
C
D
E
O
如图:
1、如图:在圆O中,∠O=50°,则∠A= .
2、如图:那个角与∠BAC相等?你还能找到哪些相等的角?
跟踪练习
25°
∠ADC。略
如图:OA,OB,OC都是⊙O的半径,∠AOB=2∠BOC.
∠ACB与∠BAC的大小有什么关系?为什么?
典例精讲
A
O
B
C
∠AOB=2∠BOC
∠ACB=2∠BAC
解:∠ACB=2∠BAC
∠BAC= ∠BOC
∠ACB= ∠AOB
如图(1),在足球比赛中,球员射中球门的难易程度与他所处的位置的射门角度的大小有关.如果在一次比赛中,小华和小勇分别处在图(2)中的A,B两点,球门的位置在线段CD,如果球在小华的脚下,此时他应该选择传给小勇还是自己射门较好?(通过尺规作图说明原因)
分析:结合图形,可以作出过点A,C,D三点的圆,则此时点B在圆外.根据三角形的外角的性质可以证明∠CAD>∠CBD.
解:设BC与圆的交点是E,则∠CAD=∠CED>∠DBE,所以还是自己射门较好.
典例精讲
船在航行过程中,船长常常通过测定角度来确定是否会遇到暗礁,如图,A
船在航行过程中,船长常常通过测定角度来确定是否会遇到暗礁.如图A,B表示灯塔,暗礁分布在经过A,B两点的一个圆形区域内,C表示一个危险临界点,∠ACB就是“危险角”,当船与两个灯塔的夹角大于“危险角”时,就有可能触礁.弓形所含的圆周角∠C=50°,问船在航行时怎样才能保证不进入暗礁区
(1)当船与两个灯塔的夹角∠α大于“危险角”时,
船位于哪个区域 为什么
(2)当船与两个灯塔的夹角∠α小于“危险角”时,
船位于哪个区域 为什么
典例精讲
解:(1)当船与两个灯塔的夹角α大于“危险角”时,船位于⊙O内,
如图(1),延长AP交⊙O于点F,连接BF,
∵∠C=∠F,∠APB>∠F,
∴∠APB>∠C,即α>∠C,
∴当船与两个灯塔的夹角α大于“危险角”时,船位于⊙O内;
(2)当船与两个灯塔的夹角α小于“危险角”时,船位于⊙O外.
如图(2),连接BE,
∵∠AEB=∠C,∠AEB>∠P,
∴∠C>∠P,即α<∠C,
∴当船与两个灯塔的夹角α小于“危险角”时,船位于⊙O外.
,则 。
1、 如图,点A,B,C,D在⊙O上, , ,
2.(2020·淮安)如图,点A,B,C在⊙O上,∠ACB=54°,则∠ABO的度数是( )
A.54° B.27° C.36° D.108°
C
70°
课堂练习
3.(2019·河南一模)如图,边长为1的小正方形网格中,⊙O的圆心在格点上,则∠AED的正切值是 .
4.如图,点A,B,C是⊙O上的三点,且四边形ABCO是平行四边形,OF⊥OC交⊙O于点F,则∠BAF等于( )
A.12.5° B.15°
C.20° D.22.5°
B
课堂练习
(1)一个概念(圆周角)
课堂小结
(2)一个定理:一条弧所对的圆周角等于该弧所对的圆心角的一半;
(3)一个推论:
同圆内,同弧或等弧所对的圆周角相等;相等的圆周角所对的弧相等。
北师版九年级下册 圆
§3.4.1 圆周角与圆心角的关系
1、理解圆周角的概念.
2、掌握圆周角的两个特征、定理和推论一的内容及简单应用.
3、继续培养学生观察、分析、想象、归纳和逻辑推理的能力.
4、渗透由“特殊到一般”,由“一般到特殊”的数学思想方法.
情境导入
足球射门小常识:
在左边比较好射门,因为用右脚踢,力道大,也很准,
在右面比较难射门,力道小.
不考虑其他因素,仅考虑射点到球门AB的张角大小时,张角越大,射门越好.
在射门游戏中(如图 3-14)、球员射口球门的难易程度与他所处的位置B
对球门AC的张角(∠ABC)有关.当球员在B、D、E处射门时、他所处的
位置对球门AC分别形成三个张角 ∠ABC,∠ADC,∠AEC.这三个角的大小
有什么关系
情境导入
新知讲解
分析: 通过观察图形。我们可以猜想出来 ∠AEC=∠ABC=∠ADC.
可为什么它们能相等?它们又叫什么角?
之前我们学习过圆心角,它有什么特征?
新知讲解
o
A
B
顶点在圆心的角叫圆心角。
o
A
B
C
顶点在圆上,并且两边都和圆相交的角叫做圆周角.
判断下列各图中,哪些是圆周角,为什么?
o
A
B
o
A
B
o
A
B
o
A
B
o
A
B
o
A
B
o
A
B
o
A
B
o
A
B
C
C
C
C
C
C
C
C
图1
图2
图3
图4
图5
图6
图7
图8
图9
跟踪练习
圆周角.GSP
如图,观察变动点D在圆周上的位置,圆周角的度数有没有变化?你能发现什么规律吗?
再分别量出图中弧AB所对的圆心角的度数,比较一下两个角的度数大小关系,你什么发现?
新知讲解
同弧所对的圆周角的度数没有变化,并且它的度数恰好等于这条弧所对的圆心角的度数的一半.
同弧所对圆周角与圆心角的关系
合作探究
将圆对折,使折痕经过圆心O和圆周角的顶点C,你能画出几种同弧(等弧)所对的圆周角和圆心角
折痕是圆周角的一条边,
折痕在圆周角的内部
折痕在圆周角的外部
(1)在圆周角的一条边上;
即
∵OC=OB,
∴∠OBC=∠C.
又∠BOA=∠OBC+∠C
∴∠BOA=2∠C
(2)在圆周角的内部.
圆心O在∠BAC的内部,作直径AD,利用(1)的结果,有
(3)在圆周角的外部.
圆心O在∠BAC的外部,作直径AD,利用(1)的结果,有
在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
圆周角定理
新知讲解
·
A
B
C
D
E
O
如图:
1、如图:在圆O中,∠O=50°,则∠A= .
2、如图:那个角与∠BAC相等?你还能找到哪些相等的角?
跟踪练习
25°
∠ADC。略
如图:OA,OB,OC都是⊙O的半径,∠AOB=2∠BOC.
∠ACB与∠BAC的大小有什么关系?为什么?
典例精讲
A
O
B
C
∠AOB=2∠BOC
∠ACB=2∠BAC
解:∠ACB=2∠BAC
∠BAC= ∠BOC
∠ACB= ∠AOB
如图(1),在足球比赛中,球员射中球门的难易程度与他所处的位置的射门角度的大小有关.如果在一次比赛中,小华和小勇分别处在图(2)中的A,B两点,球门的位置在线段CD,如果球在小华的脚下,此时他应该选择传给小勇还是自己射门较好?(通过尺规作图说明原因)
分析:结合图形,可以作出过点A,C,D三点的圆,则此时点B在圆外.根据三角形的外角的性质可以证明∠CAD>∠CBD.
解:设BC与圆的交点是E,则∠CAD=∠CED>∠DBE,所以还是自己射门较好.
典例精讲
船在航行过程中,船长常常通过测定角度来确定是否会遇到暗礁,如图,A
船在航行过程中,船长常常通过测定角度来确定是否会遇到暗礁.如图A,B表示灯塔,暗礁分布在经过A,B两点的一个圆形区域内,C表示一个危险临界点,∠ACB就是“危险角”,当船与两个灯塔的夹角大于“危险角”时,就有可能触礁.弓形所含的圆周角∠C=50°,问船在航行时怎样才能保证不进入暗礁区
(1)当船与两个灯塔的夹角∠α大于“危险角”时,
船位于哪个区域 为什么
(2)当船与两个灯塔的夹角∠α小于“危险角”时,
船位于哪个区域 为什么
典例精讲
解:(1)当船与两个灯塔的夹角α大于“危险角”时,船位于⊙O内,
如图(1),延长AP交⊙O于点F,连接BF,
∵∠C=∠F,∠APB>∠F,
∴∠APB>∠C,即α>∠C,
∴当船与两个灯塔的夹角α大于“危险角”时,船位于⊙O内;
(2)当船与两个灯塔的夹角α小于“危险角”时,船位于⊙O外.
如图(2),连接BE,
∵∠AEB=∠C,∠AEB>∠P,
∴∠C>∠P,即α<∠C,
∴当船与两个灯塔的夹角α小于“危险角”时,船位于⊙O外.
,则 。
1、 如图,点A,B,C,D在⊙O上, , ,
2.(2020·淮安)如图,点A,B,C在⊙O上,∠ACB=54°,则∠ABO的度数是( )
A.54° B.27° C.36° D.108°
C
70°
课堂练习
3.(2019·河南一模)如图,边长为1的小正方形网格中,⊙O的圆心在格点上,则∠AED的正切值是 .
4.如图,点A,B,C是⊙O上的三点,且四边形ABCO是平行四边形,OF⊥OC交⊙O于点F,则∠BAF等于( )
A.12.5° B.15°
C.20° D.22.5°
B
课堂练习
(1)一个概念(圆周角)
课堂小结
(2)一个定理:一条弧所对的圆周角等于该弧所对的圆心角的一半;
(3)一个推论:
同圆内,同弧或等弧所对的圆周角相等;相等的圆周角所对的弧相等。
