2021-2022学年北师大版数学九年级下册1.6利用三角函数测高课件(共20张PPT)
文档属性
| 名称 | 2021-2022学年北师大版数学九年级下册1.6利用三角函数测高课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-28 00:00:00 | ||
图片预览







文档简介
(共20张PPT)
北师大版数学九年级(下)
6.利用三角函数测高
第一章 直角三角形的边角关系
教学目标
重点难点
1.了解侧倾器的构造和使用方法,能使用侧倾器测量底部可以到达好底部不可以到达的物体的高度.(重点)
2.能根据物体底部是否可以到达设计不同的测量方案.(难点)
答一答
教学过程
温故知新
由直角三角形中已知的元素,求出所有未知元素的过程,叫做解直角三角形.
1.什么叫解直角三角形?
2.解直角三角形时至少要知道几个元素?
直角三角形中,除了直角外的5个元素中只要知道其中两个元素(其中至少要有一边),就可以求出其余的三个元素.
议一议
教学过程
新课引入
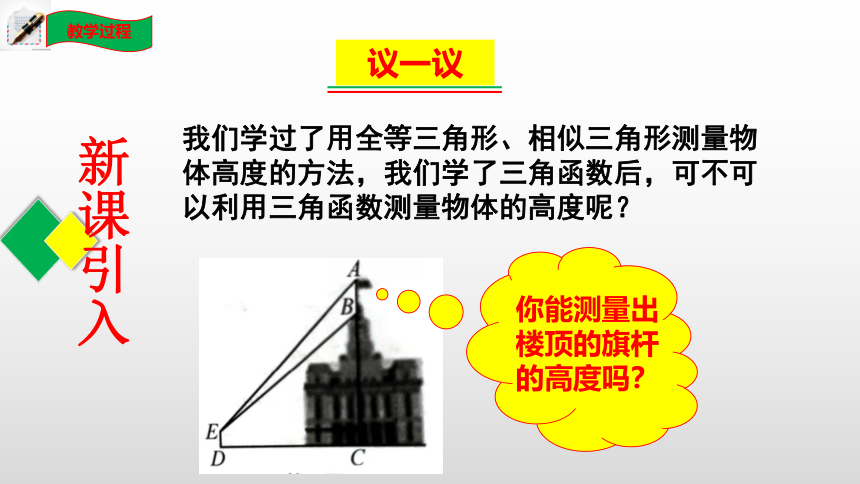
我们学过了用全等三角形、相似三角形测量物体高度的方法,我们学了三角函数后,可不可以利用三角函数测量物体的高度呢?
你能测量出楼顶的旗杆的高度吗?
议一议
教学过程
新知新授
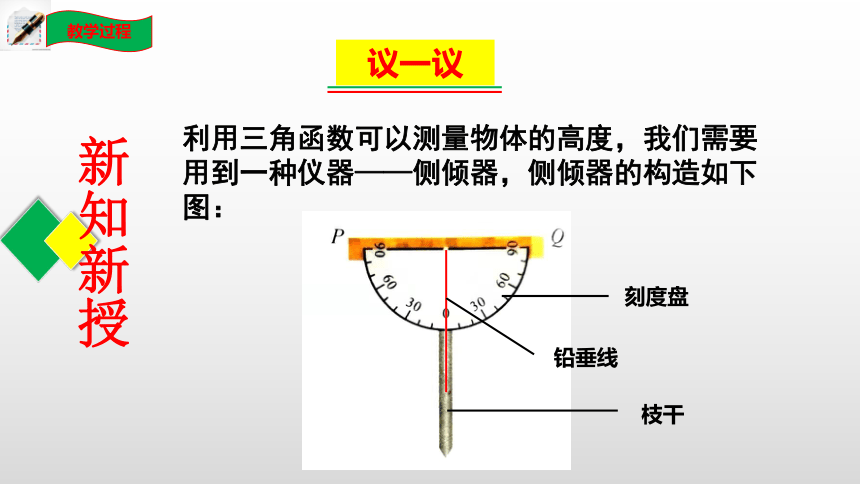
利用三角函数可以测量物体的高度,我们需要用到一种仪器——侧倾器,侧倾器的构造如下图:
刻度盘
铅垂线
枝干
做一做
教学过程
新知新授
活动一、用侧倾器测倾斜角
使用测倾器测量倾斜角的步骤如下:
1.把支杆竖直插入地面,使支杆的中心线、铅垂线和度盘的0°刻度线重合,这时度盘的顶线PQ在水平位置.
2.转动度盘,使度盘的直径对准目标M,记下此时铅垂线所指的度数
做一做
教学过程
新知新授
根据测量数据,你能求出目标M的仰角或俯角吗?说说你的理由.
M
N
P
Q
O
A
B
做一做
教学过程
新知新授
活动二、测量底部可以到达的物体的高度
测量工具:测倾器(或经纬仪、测角仪等)、皮尺等
测量步骤:1.在测点A处安置测倾器,测得M的仰角∠MCE=α.
2.量出测点A到物体底部N的水平距离AN=.
3.量出测倾器的高度AC=a(即顶线PQ成水平位置时,它与地面的距离).
做一做
教学过程
新知新授
根据测量数据,你能求出物体MN的高度吗?说说你的理由.
解:根据题意可知四边形ACEN
为矩形.∴EC=AN=,EN=AC=a
在Rt△MCE中,EM=EC tan∠MCE= tanα
∵MN=EM+EN=tanα+a.
∴物体MN的高度为 tanα+a.
做一做
教学过程
新知新授
活动三、测量底部不可以到达的物体的高度
做一做
教学过程
新知新授
测量工具:测倾器(或经纬仪、测角仪等)、皮尺等
1.在测点A处安置测倾器,测得此时M的仰角∠MCE=α.
2.在测点A与物体之间的B处安置测倾器(A、B与N在一条直线上,且A,B之间的距离可以直接测得),测得此时M的仰角∠MDE=β.
3.量出测倾器的高度AC=BD=a,以及测点A,B之间的距离AB=b.
做一做
教学过程
新知新授
根据测量数据,你能求出物体MN的高度吗?说说你的理由.
做一做
教学过程
新知新授
解:根据题意可知EN=BD=AC=a,CD=AB=b
在Rt△MCE中,EC==
在Rt△MDE中,ED==
∵CD=EC-ED,∴-=b,∴ME=
∴MN=.∴物体MN的高度为.
做一做
教学过程
例题解析
例1. 如图,甲、乙两座建筑物的水平距离BC为78m,从甲的顶部A处测得乙的顶部D处的俯角为48°,测得底部C处的俯角为58°,求甲、乙建筑物的高度AB和DC.(结果取整数,参考数据:than48°≈1.11,tan58°≈1.60)
解:过D作DE⊥AB于E,
做一做
教学过程
例题解析
E
∴AB=BC tan∠ACB=78×tan58°≈125(米)
在Rt△ABC中,∠ABC=90°,∠ACB=58°,BC=78.
根据题意可知∠ADE=48°,∠ACB=58°,
DE=BC=78米,CD=BE.
做一做
教学过程
例题解析
E
在Rt△ADE中,∠AED=90°,∠ADE=48°,DE=78.
∴AE=DE tan∠ADE=78×÷tan48°≈87(米)
∵AB=AE+BE
∴BE=AB-AE=125-87=38(米)
∴甲、乙建筑物的高度分别约为125米、38米.
记一记
教学过程
课堂小结
测量底部可以到达的物体的高度
测量步骤:1.在测点A处安置测倾器,测得M的仰角∠MCE=α.
2.量出测点A到物体底部N的水平距离AN=.
3.量出测倾器的高度AC=a(即顶线PQ成水平位置时,它与地面的距离).
物体MN的高度为 tanα+a.
记一记
教学过程
课堂小结
测量底部不可以到达的物体的高度
1.在测点A处安置测倾器,测得此时M的仰角∠MCE=α.
2.在测点A与物体之间的B处安置测倾器(A、B与N在一条直线上,且A,B之间的距离可以直接测得),测得此时M的仰角∠MDE=β.
3.量出测倾器的高度AC=BD=a,以及测点A,B之间的距离AB=b.
物体MN的高度为.
分层作业
教学过程
课后巩固
完成练习册相关作业.
教学过程
结束新课
感谢聆听
北师大版数学九年级(下)
6.利用三角函数测高
第一章 直角三角形的边角关系
教学目标
重点难点
1.了解侧倾器的构造和使用方法,能使用侧倾器测量底部可以到达好底部不可以到达的物体的高度.(重点)
2.能根据物体底部是否可以到达设计不同的测量方案.(难点)
答一答
教学过程
温故知新
由直角三角形中已知的元素,求出所有未知元素的过程,叫做解直角三角形.
1.什么叫解直角三角形?
2.解直角三角形时至少要知道几个元素?
直角三角形中,除了直角外的5个元素中只要知道其中两个元素(其中至少要有一边),就可以求出其余的三个元素.
议一议
教学过程
新课引入
我们学过了用全等三角形、相似三角形测量物体高度的方法,我们学了三角函数后,可不可以利用三角函数测量物体的高度呢?
你能测量出楼顶的旗杆的高度吗?
议一议
教学过程
新知新授
利用三角函数可以测量物体的高度,我们需要用到一种仪器——侧倾器,侧倾器的构造如下图:
刻度盘
铅垂线
枝干
做一做
教学过程
新知新授
活动一、用侧倾器测倾斜角
使用测倾器测量倾斜角的步骤如下:
1.把支杆竖直插入地面,使支杆的中心线、铅垂线和度盘的0°刻度线重合,这时度盘的顶线PQ在水平位置.
2.转动度盘,使度盘的直径对准目标M,记下此时铅垂线所指的度数
做一做
教学过程
新知新授
根据测量数据,你能求出目标M的仰角或俯角吗?说说你的理由.
M
N
P
Q
O
A
B
做一做
教学过程
新知新授
活动二、测量底部可以到达的物体的高度
测量工具:测倾器(或经纬仪、测角仪等)、皮尺等
测量步骤:1.在测点A处安置测倾器,测得M的仰角∠MCE=α.
2.量出测点A到物体底部N的水平距离AN=.
3.量出测倾器的高度AC=a(即顶线PQ成水平位置时,它与地面的距离).
做一做
教学过程
新知新授
根据测量数据,你能求出物体MN的高度吗?说说你的理由.
解:根据题意可知四边形ACEN
为矩形.∴EC=AN=,EN=AC=a
在Rt△MCE中,EM=EC tan∠MCE= tanα
∵MN=EM+EN=tanα+a.
∴物体MN的高度为 tanα+a.
做一做
教学过程
新知新授
活动三、测量底部不可以到达的物体的高度
做一做
教学过程
新知新授
测量工具:测倾器(或经纬仪、测角仪等)、皮尺等
1.在测点A处安置测倾器,测得此时M的仰角∠MCE=α.
2.在测点A与物体之间的B处安置测倾器(A、B与N在一条直线上,且A,B之间的距离可以直接测得),测得此时M的仰角∠MDE=β.
3.量出测倾器的高度AC=BD=a,以及测点A,B之间的距离AB=b.
做一做
教学过程
新知新授
根据测量数据,你能求出物体MN的高度吗?说说你的理由.
做一做
教学过程
新知新授
解:根据题意可知EN=BD=AC=a,CD=AB=b
在Rt△MCE中,EC==
在Rt△MDE中,ED==
∵CD=EC-ED,∴-=b,∴ME=
∴MN=.∴物体MN的高度为.
做一做
教学过程
例题解析
例1. 如图,甲、乙两座建筑物的水平距离BC为78m,从甲的顶部A处测得乙的顶部D处的俯角为48°,测得底部C处的俯角为58°,求甲、乙建筑物的高度AB和DC.(结果取整数,参考数据:than48°≈1.11,tan58°≈1.60)
解:过D作DE⊥AB于E,
做一做
教学过程
例题解析
E
∴AB=BC tan∠ACB=78×tan58°≈125(米)
在Rt△ABC中,∠ABC=90°,∠ACB=58°,BC=78.
根据题意可知∠ADE=48°,∠ACB=58°,
DE=BC=78米,CD=BE.
做一做
教学过程
例题解析
E
在Rt△ADE中,∠AED=90°,∠ADE=48°,DE=78.
∴AE=DE tan∠ADE=78×÷tan48°≈87(米)
∵AB=AE+BE
∴BE=AB-AE=125-87=38(米)
∴甲、乙建筑物的高度分别约为125米、38米.
记一记
教学过程
课堂小结
测量底部可以到达的物体的高度
测量步骤:1.在测点A处安置测倾器,测得M的仰角∠MCE=α.
2.量出测点A到物体底部N的水平距离AN=.
3.量出测倾器的高度AC=a(即顶线PQ成水平位置时,它与地面的距离).
物体MN的高度为 tanα+a.
记一记
教学过程
课堂小结
测量底部不可以到达的物体的高度
1.在测点A处安置测倾器,测得此时M的仰角∠MCE=α.
2.在测点A与物体之间的B处安置测倾器(A、B与N在一条直线上,且A,B之间的距离可以直接测得),测得此时M的仰角∠MDE=β.
3.量出测倾器的高度AC=BD=a,以及测点A,B之间的距离AB=b.
物体MN的高度为.
分层作业
教学过程
课后巩固
完成练习册相关作业.
教学过程
结束新课
感谢聆听
