鲁教版 数学 九年级上册 2.1 锐角三角函数课件(共26张PPT)
文档属性
| 名称 | 鲁教版 数学 九年级上册 2.1 锐角三角函数课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 291.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-28 14:00:06 | ||
图片预览



文档简介
(共26张PPT)
1 锐角三角函数(1)
第二章 直角三角形的边角关系
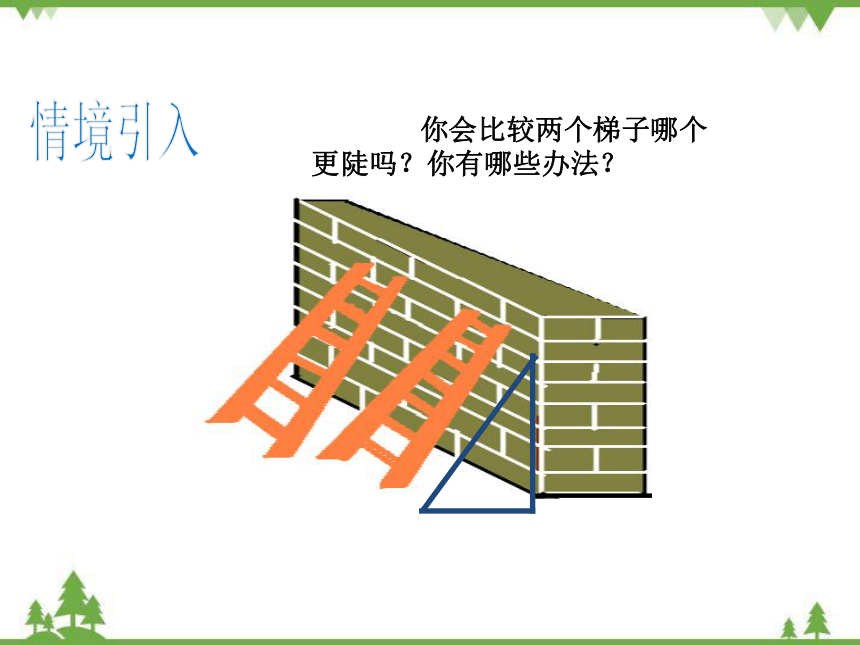
生活中的梯子
你会比较两个梯子哪个更陡吗?你有哪些办法?
情境引入
自主预习
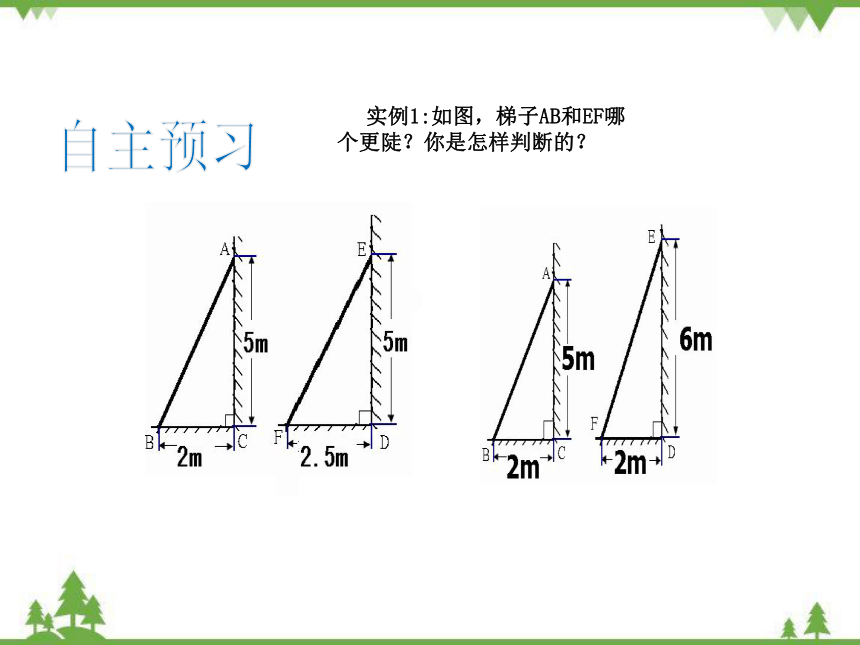
实例1:如图,梯子AB和EF哪个更陡?你是怎样判断的?
3m
4m
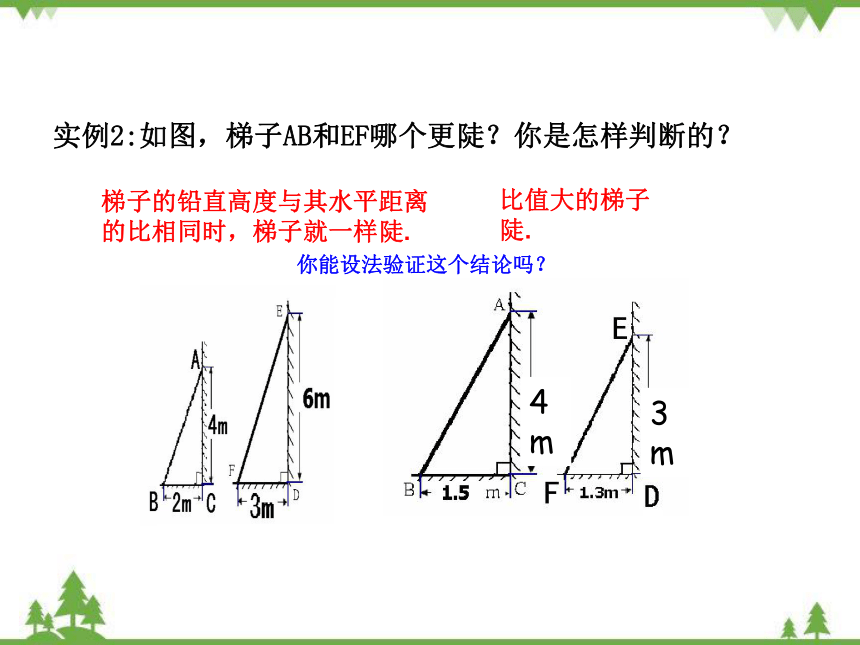
实例2:如图,梯子AB和EF哪个更陡?你是怎样判断的?
梯子的铅直高度与其水平距离的比相同时,梯子就一样陡.
比值大的梯子陡.
你能设法验证这个结论吗?
如图,小明想通过测量 及 ,算出他们的比,来说明梯子的倾斜程度;而小亮则认为,通过测量 及 ,算出他们的比,也能说明梯子的倾斜程度,你同意小亮的看法吗?
A
B1
C1
C2
B2
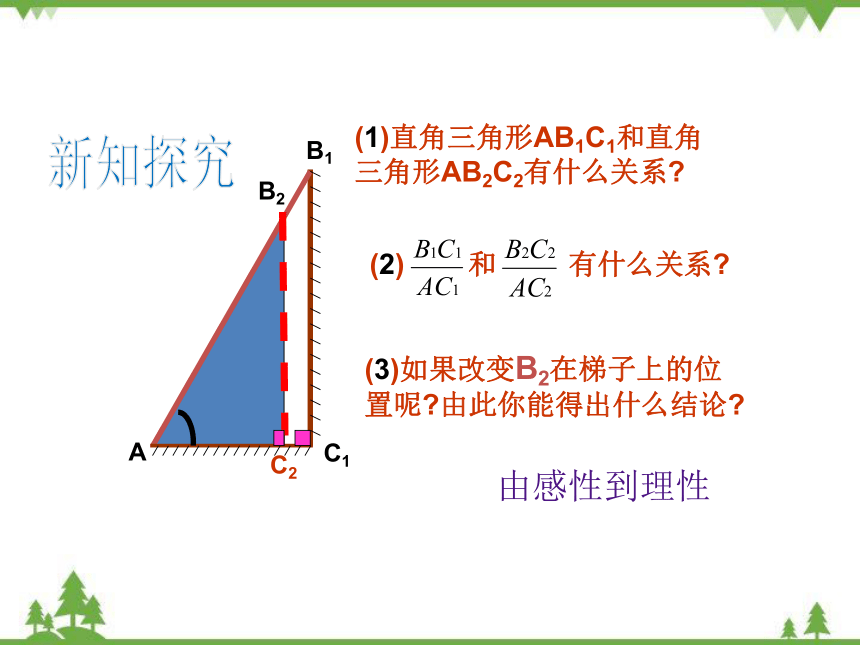
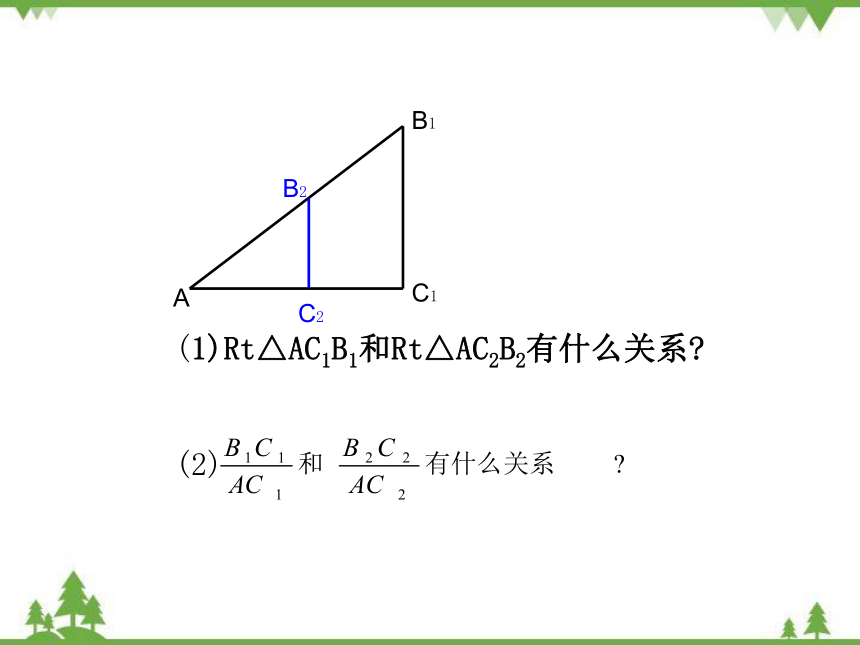
(1)直角三角形AB1C1和直角三角形AB2C2有什么关系
(2) 和 有什么关系
(3)如果改变B2在梯子上的位置呢 由此你能得出什么结论
由感性到理性
新知探究
A
B1
C1
C2
B2
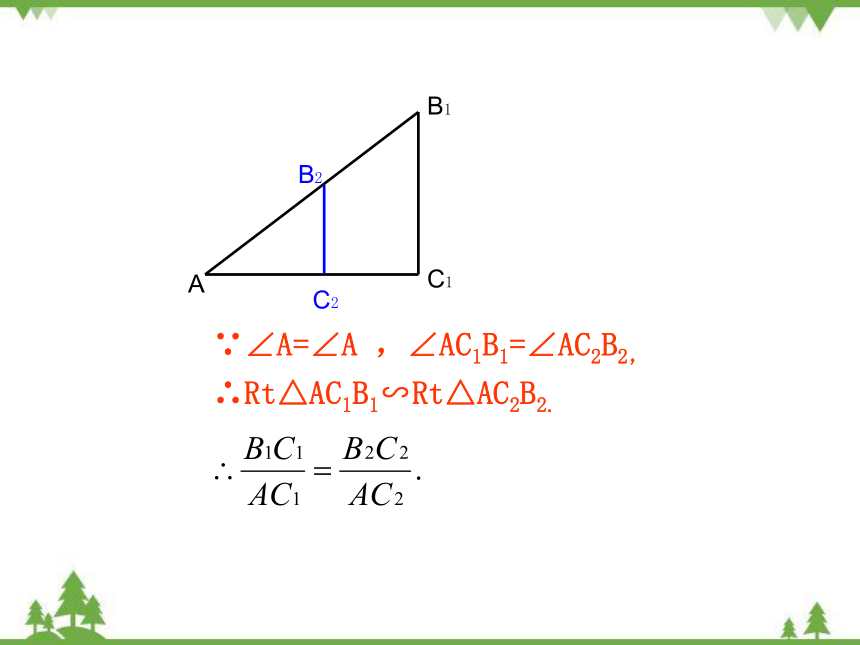
(1)Rt△AC1B1和Rt△AC2B2有什么关系
(2)
A
B1
C1
C2
B2
∵∠A=∠A ,∠AC1B1=∠AC2B2,
∴Rt△AC1B1∽Rt△AC2B2.
在直角三角形中,若一个锐角确定,那么这个角对边与邻边的比值也是确定的.
A
B
C
∠A的对边
∠A的邻边
∠A的对边
∠A的邻边
tanA
∠A的正切
在Rt△ABC中,
如果
锐角A确定,
那么
∠A的对边与邻边的比
随之确定,
这个比叫做
∠A的正切.
记作:tanA
读?
思考 梯子的倾斜程度与tanA有关系吗?
(1) tanA是在直角三角形中定义的,∠A是一个锐角(注意构造直角三角形).
(2)tanA是一个完整的符号,它表示∠A的正切,记号里习惯省去角的符号“∠”.
注意:
(3) tanA是一个比值(直角边之比,注意比的顺序);且tanA﹥0,无单位.
(4) tanA的大小只与∠A的大小有关,而与直角三角形的大小无关.
议一议:
梯子的倾斜程度与tanB有什么关系?
tanB的值越大,梯子越陡,∠B越大;
例1 如图表示两个自动扶梯,哪一个自动扶梯比较陡?
乙
甲
解:甲梯中,
tanα=
乙梯中 tanβ=
因为tanβ>tanα,所以乙梯更陡.
例2 在△ABC中,∠C=90°,BC=12cm,AB=20cm,求tanA和tanB的值.
20
12
tanA=
tanB=
.
解:在△ABC中,∠C=90°,所以AC= =16(cm),
正切通常也用来描述山坡的坡度.(坡度:铅直高度与水平宽度的比,也称为坡比)
E
F
A
B
C
D
50m
60m
tanA=5/6
1、判断对错:
如图1, (1) tanA= ( )
(2) tanB= ( )
图1
错
错
随堂练习
怎样解答
(4) tanB= ( )
如图2
图2
(3) tanA=0.7m ( )
错
对
2、在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,tanA的值( )
A、扩大100倍 B、缩小100倍 C、不变 D、不能确定
C
3.如图,△ABC是等腰三角形,AB=BC,你能根据图中所给数据求出tanC吗?
4
tanC=
4. 在等腰△ABC中,AB=AC=13,BC=10,求tanB.
13
13
10
D
5
12
tanB=12/5
5.如图∠C=90°CD⊥AB,
tanB=
CD
BD
AC
BC
AD
CD
1、正切的定义.
2、梯子的倾斜程度与tanA的关系 (∠A和tanA之间的关系).
3、数形结合的方法;构造直角三角形的意识.
知识梳理
1 锐角三角函数(1)
第二章 直角三角形的边角关系
生活中的梯子
你会比较两个梯子哪个更陡吗?你有哪些办法?
情境引入
自主预习
实例1:如图,梯子AB和EF哪个更陡?你是怎样判断的?
3m
4m
实例2:如图,梯子AB和EF哪个更陡?你是怎样判断的?
梯子的铅直高度与其水平距离的比相同时,梯子就一样陡.
比值大的梯子陡.
你能设法验证这个结论吗?
如图,小明想通过测量 及 ,算出他们的比,来说明梯子的倾斜程度;而小亮则认为,通过测量 及 ,算出他们的比,也能说明梯子的倾斜程度,你同意小亮的看法吗?
A
B1
C1
C2
B2
(1)直角三角形AB1C1和直角三角形AB2C2有什么关系
(2) 和 有什么关系
(3)如果改变B2在梯子上的位置呢 由此你能得出什么结论
由感性到理性
新知探究
A
B1
C1
C2
B2
(1)Rt△AC1B1和Rt△AC2B2有什么关系
(2)
A
B1
C1
C2
B2
∵∠A=∠A ,∠AC1B1=∠AC2B2,
∴Rt△AC1B1∽Rt△AC2B2.
在直角三角形中,若一个锐角确定,那么这个角对边与邻边的比值也是确定的.
A
B
C
∠A的对边
∠A的邻边
∠A的对边
∠A的邻边
tanA
∠A的正切
在Rt△ABC中,
如果
锐角A确定,
那么
∠A的对边与邻边的比
随之确定,
这个比叫做
∠A的正切.
记作:tanA
读?
思考 梯子的倾斜程度与tanA有关系吗?
(1) tanA是在直角三角形中定义的,∠A是一个锐角(注意构造直角三角形).
(2)tanA是一个完整的符号,它表示∠A的正切,记号里习惯省去角的符号“∠”.
注意:
(3) tanA是一个比值(直角边之比,注意比的顺序);且tanA﹥0,无单位.
(4) tanA的大小只与∠A的大小有关,而与直角三角形的大小无关.
议一议:
梯子的倾斜程度与tanB有什么关系?
tanB的值越大,梯子越陡,∠B越大;
例1 如图表示两个自动扶梯,哪一个自动扶梯比较陡?
乙
甲
解:甲梯中,
tanα=
乙梯中 tanβ=
因为tanβ>tanα,所以乙梯更陡.
例2 在△ABC中,∠C=90°,BC=12cm,AB=20cm,求tanA和tanB的值.
20
12
tanA=
tanB=
.
解:在△ABC中,∠C=90°,所以AC= =16(cm),
正切通常也用来描述山坡的坡度.(坡度:铅直高度与水平宽度的比,也称为坡比)
E
F
A
B
C
D
50m
60m
tanA=5/6
1、判断对错:
如图1, (1) tanA= ( )
(2) tanB= ( )
图1
错
错
随堂练习
怎样解答
(4) tanB= ( )
如图2
图2
(3) tanA=0.7m ( )
错
对
2、在Rt△ABC中,锐角A的对边和邻边同时扩大100倍,tanA的值( )
A、扩大100倍 B、缩小100倍 C、不变 D、不能确定
C
3.如图,△ABC是等腰三角形,AB=BC,你能根据图中所给数据求出tanC吗?
4
tanC=
4. 在等腰△ABC中,AB=AC=13,BC=10,求tanB.
13
13
10
D
5
12
tanB=12/5
5.如图∠C=90°CD⊥AB,
tanB=
CD
BD
AC
BC
AD
CD
1、正切的定义.
2、梯子的倾斜程度与tanA的关系 (∠A和tanA之间的关系).
3、数形结合的方法;构造直角三角形的意识.
知识梳理
