青岛版数学九年级上册 3.4直线与圆的位置关系 课件(共8张PPT)
文档属性
| 名称 | 青岛版数学九年级上册 3.4直线与圆的位置关系 课件(共8张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 170.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-28 14:02:46 | ||
图片预览

文档简介
(共8张PPT)
2.5直线与圆的位置关系(3)
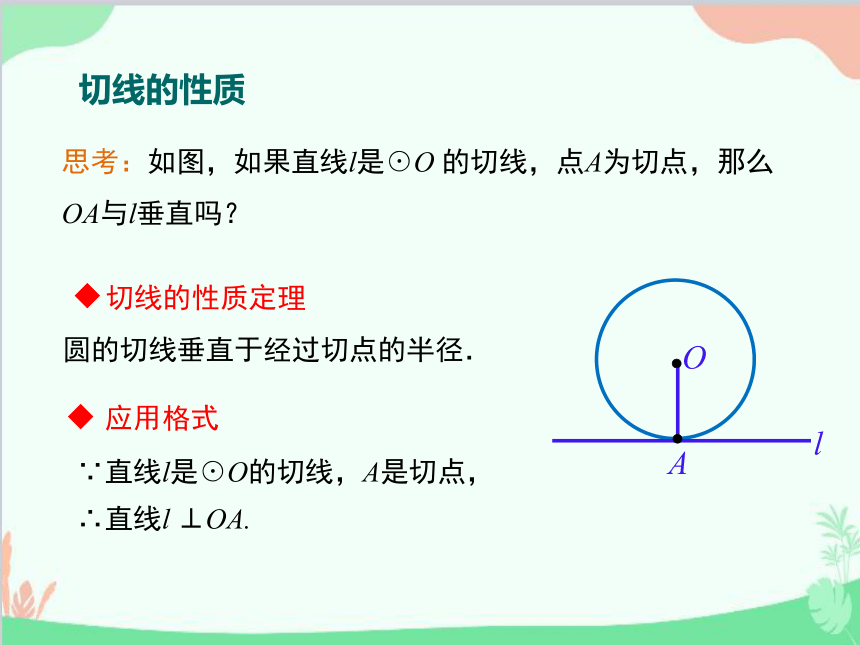
思考:如图,如果直线l是☉O 的切线,点A为切点,那么OA与l垂直吗?
A
l
O
∵直线l是☉O的切线,A是切点,
∴直线l ⊥OA.
切线的性质
切线的性质定理
圆的切线垂直于经过切点的半径.
应用格式
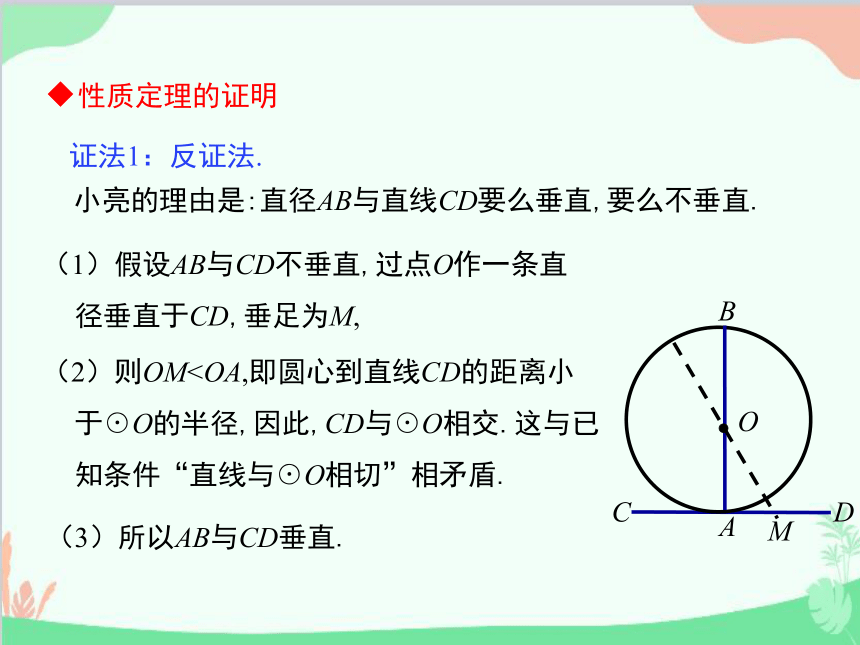
小亮的理由是:直径AB与直线CD要么垂直,要么不垂直.
(1)假设AB与CD不垂直,过点O作一条直径垂直于CD,垂足为M,
(2)则OMC
D
B
O
A
(3)所以AB与CD垂直.
M
证法1:反证法.
性质定理的证明
C
D
O
A
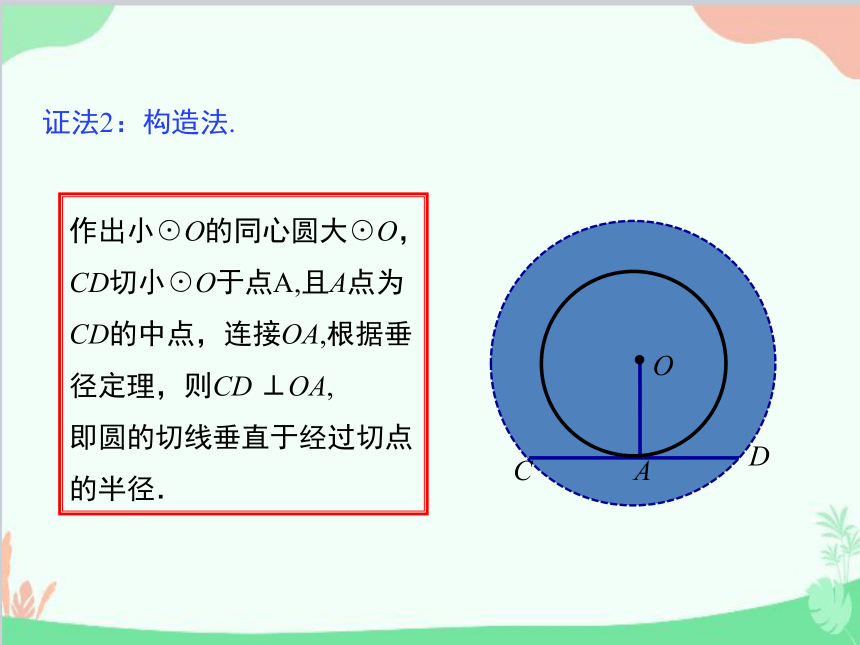
证法2:构造法.
作出小☉O的同心圆大☉O,CD切小☉O于点A,且A点为CD的中点,连接OA,根据垂径定理,则CD ⊥OA,
即圆的切线垂直于经过切点的半径.
例:如图,AB为☉O的切线,B为切点,若∠OAB=30°,AO=6,则AB= .
解:如图,连接OB.
∵AB为☉O的切线,B为切点,
∴OB⊥AB.
在Rt△ABO中,∠ABO=90°,
∠OAB=30°,AO=6,∴OB=AO=3.
∴AB===3.
如图,直线l切☉O于点A,点P为直线l上一点,直线PO交☉O于点C,B,点D在线段AP上,连接DB,且DA=DB.
(1)求证:DB为☉O的切线;
(2)若AD=1,PB=BO,求弦AC的长.
练习
解:(1)证明:连接OD,如图
∵PA 为☉O的切线,
∴∠OAD=90°.
∵OA=OB,DA=DB,DO=DO,
∴△OAD≌△OBD.
∴∠OBD=∠OAD=90°,
∴DB为☉O的切线.
(2)解:在Rt△OAP中,
∵PB=BO=OA,∴∠OPA=30°.
∴∠POA=60°=2∠C,
∴∠C=∠OPA=30°,∴AC=PA.
又∵AD=1,
∴PD=2BD=2AD=2.
∴AC=PA=AD+PD=1+2=3.
切线的
性质
有1个公共点
d=r
性质定理
圆的切线垂直于经过切点的半径
有切线时常用辅助线
添加方法:
见切线,连切点,得垂直.
【小结】
2.5直线与圆的位置关系(3)
思考:如图,如果直线l是☉O 的切线,点A为切点,那么OA与l垂直吗?
A
l
O
∵直线l是☉O的切线,A是切点,
∴直线l ⊥OA.
切线的性质
切线的性质定理
圆的切线垂直于经过切点的半径.
应用格式
小亮的理由是:直径AB与直线CD要么垂直,要么不垂直.
(1)假设AB与CD不垂直,过点O作一条直径垂直于CD,垂足为M,
(2)则OM
D
B
O
A
(3)所以AB与CD垂直.
M
证法1:反证法.
性质定理的证明
C
D
O
A
证法2:构造法.
作出小☉O的同心圆大☉O,CD切小☉O于点A,且A点为CD的中点,连接OA,根据垂径定理,则CD ⊥OA,
即圆的切线垂直于经过切点的半径.
例:如图,AB为☉O的切线,B为切点,若∠OAB=30°,AO=6,则AB= .
解:如图,连接OB.
∵AB为☉O的切线,B为切点,
∴OB⊥AB.
在Rt△ABO中,∠ABO=90°,
∠OAB=30°,AO=6,∴OB=AO=3.
∴AB===3.
如图,直线l切☉O于点A,点P为直线l上一点,直线PO交☉O于点C,B,点D在线段AP上,连接DB,且DA=DB.
(1)求证:DB为☉O的切线;
(2)若AD=1,PB=BO,求弦AC的长.
练习
解:(1)证明:连接OD,如图
∵PA 为☉O的切线,
∴∠OAD=90°.
∵OA=OB,DA=DB,DO=DO,
∴△OAD≌△OBD.
∴∠OBD=∠OAD=90°,
∴DB为☉O的切线.
(2)解:在Rt△OAP中,
∵PB=BO=OA,∴∠OPA=30°.
∴∠POA=60°=2∠C,
∴∠C=∠OPA=30°,∴AC=PA.
又∵AD=1,
∴PD=2BD=2AD=2.
∴AC=PA=AD+PD=1+2=3.
切线的
性质
有1个公共点
d=r
性质定理
圆的切线垂直于经过切点的半径
有切线时常用辅助线
添加方法:
见切线,连切点,得垂直.
【小结】
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
