人教八下数学19.2.3一元一次不等式与一次函数习题精选(word版、含答案)
文档属性
| 名称 | 人教八下数学19.2.3一元一次不等式与一次函数习题精选(word版、含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 133.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-28 00:00:00 | ||
图片预览

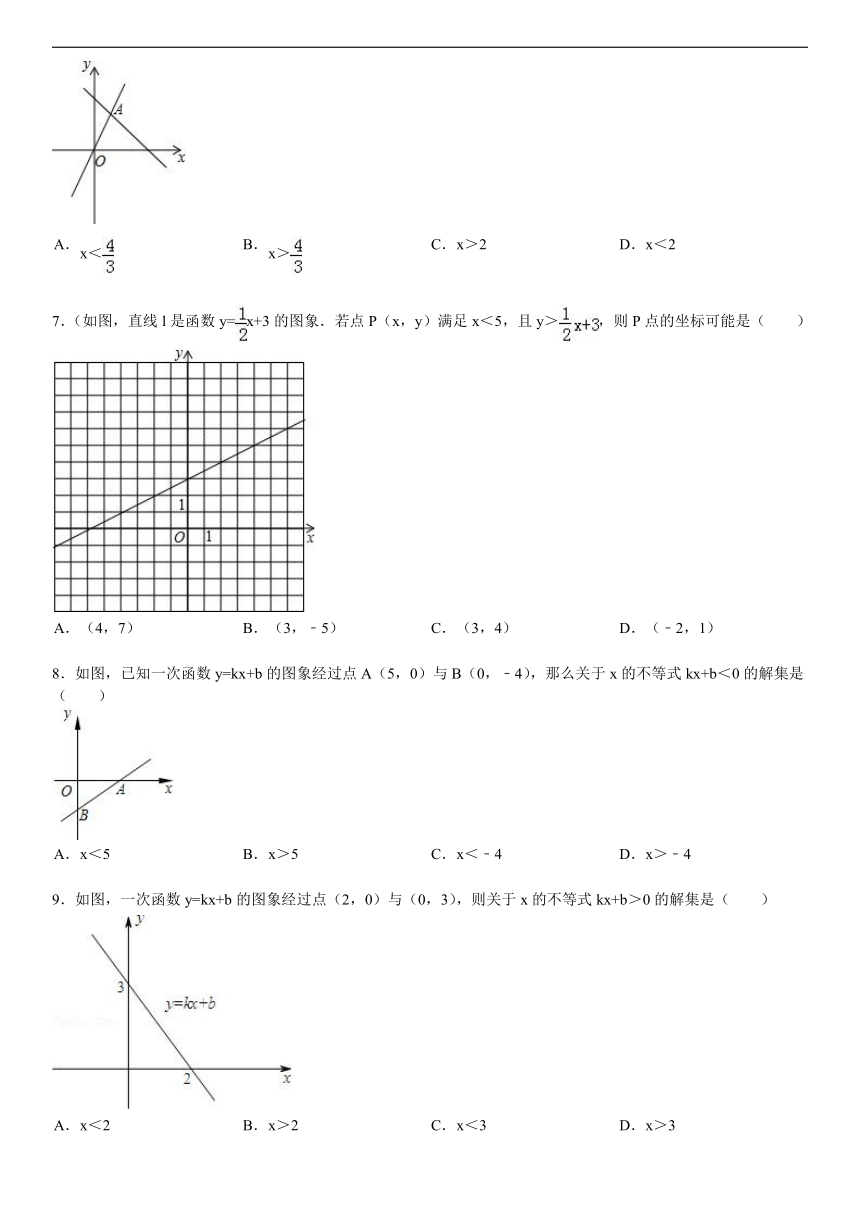
文档简介
一元一次不等式与一次函数
1.如图,函数y=2x和y=ax+4的图象相交于点A(m,3),则不等式2x<ax+4的解集为( )
A. x< B. x<3 C. x> D. x>3
2.已知一次函数y=ax+b的图象过第一、二、四象限,且与x轴交于点(2,0),则关于x的不等式a(x﹣1)﹣b>0的解集为( )
A. x<﹣1 B. x>﹣1 C. x>1 D. x<1
3.如图,直线y1=k1x+a与y2=k2x+b的交点坐标为(1,2),则使y1<y2的x的取值范围为( )
A. x>1 B. x>2 C. x<1 D. x<2
4.直线l1:y=k1x+b与直线l2:y=k2x+c在同一平面直角坐标系中的图象如图所示,则关于x的不等式k1x+b<k2x+c的解集为( )
A. x>1 B. x<1 C. x>﹣2 D. x<﹣2
5.如图,一次函数y=kx+b的图象经过A、B两点,则kx+b>0解集是( )
A. x>0 B. x>﹣3 C. x>2 D. ﹣3<x<2
6.如图,函数y=kx和y=﹣x+3的图象相交于(a,2),则不等式kx<﹣x+3的解集为( )
A. x< B. x> C. x>2 D. x<2
7.(如图,直线l是函数y=x+3的图象.若点P(x,y)满足x<5,且y>,则P点的坐标可能是( )
A. (4,7) B. (3,﹣5) C. (3,4) D. (﹣2,1)
8.如图,已知一次函数y=kx+b的图象经过点A(5,0)与B(0,﹣4),那么关于x的不等式kx+b<0的解集是( )
A. x<5 B. x>5 C. x<﹣4 D. x>﹣4
9.如图,一次函数y=kx+b的图象经过点(2,0)与(0,3),则关于x的不等式kx+b>0的解集是( )
A. x<2 B. x>2 C. x<3 D. x>3
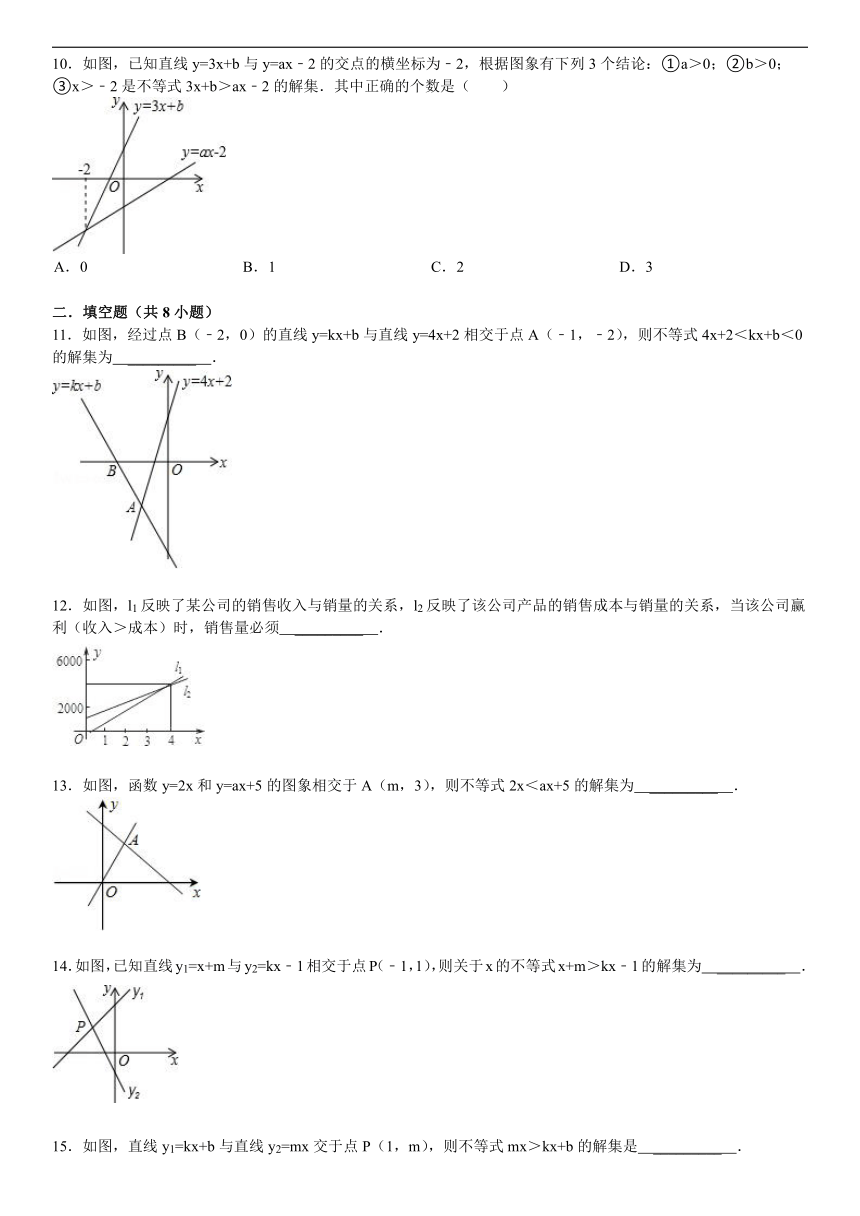
10.如图,已知直线y=3x+b与y=ax﹣2的交点的横坐标为﹣2,根据图象有下列3个结论:①a>0;②b>0;③x>﹣2是不等式3x+b>ax﹣2的解集.其中正确的个数是( )
A. 0 B. 1 C. 2 D. 3
二.填空题(共8小题)
11.如图,经过点B(﹣2,0)的直线y=kx+b与直线y=4x+2相交于点A(﹣1,﹣2),则不等式4x+2<kx+b<0的解集为 _________ .
12.如图,l1反映了某公司的销售收入与销量的关系,l2反映了该公司产品的销售成本与销量的关系,当该公司赢利(收入>成本)时,销售量必须 _________ .
13.如图,函数y=2x和y=ax+5的图象相交于A(m,3),则不等式2x<ax+5的解集为 _________ .
14.如图,已知直线y1=x+m与y2=kx﹣1相交于点P(﹣1,1),则关于x的不等式x+m>kx﹣1的解集为 _________ .
15.如图,直线y1=kx+b与直线y2=mx交于点P(1,m),则不等式mx>kx+b的解集是 _________ .
16.如图,已知函数y=x+b和y=ax+3的图象相交于点P,则关于x的不等式x+b<ax+3的解集为 _________ .
17.如图,直线y=kx+b经过点A(﹣1,1)和点B(﹣4,0),则不等式0<kx+b<﹣x的解集为 _________ .
18.如图,直线y=kx+b交坐标轴于A(﹣3,0)、B(0,5)两点,则不等式﹣kx﹣b<0的解集是 _________ .
三.解答题
19.在平面直角坐标系中,直线y=kx﹣15经过点(4,﹣3),求不等式kx﹣15≥0的解.
20.如图,直线l1与l2相交于点P,点P横坐标为﹣1,l1的解析表达式为y=x+3,且l1与y轴交于点A,l2与y轴交于点B,点A与点B恰好关于x轴对称.
(1)求点B的坐标;
(2)求直线l2的解析表达式;
(3)若点M为直线l2上一动点,直接写出使△MAB的面积是△PAB的面积的的点M的坐标;
(4)当x为何值时,l1,l2表示的两个函数的函数值都大于0?
21.已知:直线l1的解析式为y1=x+1,直线l2的解析式为y2=ax+b(a≠0);两条直线如图所示,这两个图象的交点在y轴上,直线l2与x轴的交点B的坐标为(2,0)
(1)求a,b的值;
(2)求使得y1、y2的值都大于0的取值范围;
(3)求这两条直线与x轴所围成的△ABC的面积是多少?
(4)在直线AC上是否存在异于点C的另一点P,使得△ABC与△ABP的面积相等?请直接写出点P的坐标.
22.如图,直线y=kx+b经过点A(0,5),B(1,4).
(1)求直线AB的解析式;
(2)若直线y=2x﹣4与直线AB相交于点C,求点C的坐标;
(3)根据图象,写出关于x的不等式2x﹣4≥kx+b的解集.
AACBBAAAAD
﹣2<x<﹣1 . 大于4 . x< . x>﹣1 .x>1 . x<1 . ﹣4<x<﹣1 . x>﹣
19 x≥5.
20. 解:(1)当x=0时,x+3=0+3=3,
∴点A的坐标是(0,3),
∵点A与点B恰好关于x轴对称,
∴B点坐标为(0,﹣3);
(2)∵点P横坐标为﹣1,
∴(﹣1)+3=,
∴点P的坐标是(﹣1,),
设直线l2的解析式为y=kx+b,
则,
解得,
∴直线l2的解析式为y=﹣x﹣3;
(3)∵点P横坐标是﹣1,△MAB的面积是△PAB的面积的,
∴点M的横坐标的长度是,
①当横坐标是﹣时,y=(﹣)×(﹣)﹣3=﹣3=﹣,
②当横坐标是时,y=(﹣)×﹣3=﹣﹣3=﹣,
∴M点的坐标是(﹣,﹣)或(,﹣);
(4)l1:y=x+3,当y=0时,x+3=0,解得x=﹣6,
l2:y=﹣x﹣3,当y=0时,﹣x﹣3=0,
解得x=﹣,
∴当﹣6<x<﹣时,l1、l2表示的两个函数的函数值都大于0.
21 解:(1)由直线l1的解析式为y1=x+1,可求得C(0,1);
则依题意可得:,
解得:.(2)由(1)知,直线l2:y=﹣x+1;
∵y1=x+1>0,∴x>﹣1;
∵;
∴﹣1<x<2.
(3)由题意知A(﹣1,0),则AB=3,且OC=1;
∴S△ABC=AB OC=.
(4)由于△ABC、△ABP同底,若面积相等,则P点纵坐标为﹣1,代入直线l1可求得:
P的坐标为(﹣2,﹣1).
22. 解:(1)∵直线y=﹣kx+b经过点A(5,0)、B(1,4),
∴,
解方程组得,
∴直线AB的解析式为y=﹣x+5;
(2)∵直线y=2x﹣4与直线AB相交于点C,
∴解方程组,
解得,
∴点C的坐标为(3,2);(3)由图可知,x≥3时,2x﹣4≥kx+b.
1.如图,函数y=2x和y=ax+4的图象相交于点A(m,3),则不等式2x<ax+4的解集为( )
A. x< B. x<3 C. x> D. x>3
2.已知一次函数y=ax+b的图象过第一、二、四象限,且与x轴交于点(2,0),则关于x的不等式a(x﹣1)﹣b>0的解集为( )
A. x<﹣1 B. x>﹣1 C. x>1 D. x<1
3.如图,直线y1=k1x+a与y2=k2x+b的交点坐标为(1,2),则使y1<y2的x的取值范围为( )
A. x>1 B. x>2 C. x<1 D. x<2
4.直线l1:y=k1x+b与直线l2:y=k2x+c在同一平面直角坐标系中的图象如图所示,则关于x的不等式k1x+b<k2x+c的解集为( )
A. x>1 B. x<1 C. x>﹣2 D. x<﹣2
5.如图,一次函数y=kx+b的图象经过A、B两点,则kx+b>0解集是( )
A. x>0 B. x>﹣3 C. x>2 D. ﹣3<x<2
6.如图,函数y=kx和y=﹣x+3的图象相交于(a,2),则不等式kx<﹣x+3的解集为( )
A. x< B. x> C. x>2 D. x<2
7.(如图,直线l是函数y=x+3的图象.若点P(x,y)满足x<5,且y>,则P点的坐标可能是( )
A. (4,7) B. (3,﹣5) C. (3,4) D. (﹣2,1)
8.如图,已知一次函数y=kx+b的图象经过点A(5,0)与B(0,﹣4),那么关于x的不等式kx+b<0的解集是( )
A. x<5 B. x>5 C. x<﹣4 D. x>﹣4
9.如图,一次函数y=kx+b的图象经过点(2,0)与(0,3),则关于x的不等式kx+b>0的解集是( )
A. x<2 B. x>2 C. x<3 D. x>3
10.如图,已知直线y=3x+b与y=ax﹣2的交点的横坐标为﹣2,根据图象有下列3个结论:①a>0;②b>0;③x>﹣2是不等式3x+b>ax﹣2的解集.其中正确的个数是( )
A. 0 B. 1 C. 2 D. 3
二.填空题(共8小题)
11.如图,经过点B(﹣2,0)的直线y=kx+b与直线y=4x+2相交于点A(﹣1,﹣2),则不等式4x+2<kx+b<0的解集为 _________ .
12.如图,l1反映了某公司的销售收入与销量的关系,l2反映了该公司产品的销售成本与销量的关系,当该公司赢利(收入>成本)时,销售量必须 _________ .
13.如图,函数y=2x和y=ax+5的图象相交于A(m,3),则不等式2x<ax+5的解集为 _________ .
14.如图,已知直线y1=x+m与y2=kx﹣1相交于点P(﹣1,1),则关于x的不等式x+m>kx﹣1的解集为 _________ .
15.如图,直线y1=kx+b与直线y2=mx交于点P(1,m),则不等式mx>kx+b的解集是 _________ .
16.如图,已知函数y=x+b和y=ax+3的图象相交于点P,则关于x的不等式x+b<ax+3的解集为 _________ .
17.如图,直线y=kx+b经过点A(﹣1,1)和点B(﹣4,0),则不等式0<kx+b<﹣x的解集为 _________ .
18.如图,直线y=kx+b交坐标轴于A(﹣3,0)、B(0,5)两点,则不等式﹣kx﹣b<0的解集是 _________ .
三.解答题
19.在平面直角坐标系中,直线y=kx﹣15经过点(4,﹣3),求不等式kx﹣15≥0的解.
20.如图,直线l1与l2相交于点P,点P横坐标为﹣1,l1的解析表达式为y=x+3,且l1与y轴交于点A,l2与y轴交于点B,点A与点B恰好关于x轴对称.
(1)求点B的坐标;
(2)求直线l2的解析表达式;
(3)若点M为直线l2上一动点,直接写出使△MAB的面积是△PAB的面积的的点M的坐标;
(4)当x为何值时,l1,l2表示的两个函数的函数值都大于0?
21.已知:直线l1的解析式为y1=x+1,直线l2的解析式为y2=ax+b(a≠0);两条直线如图所示,这两个图象的交点在y轴上,直线l2与x轴的交点B的坐标为(2,0)
(1)求a,b的值;
(2)求使得y1、y2的值都大于0的取值范围;
(3)求这两条直线与x轴所围成的△ABC的面积是多少?
(4)在直线AC上是否存在异于点C的另一点P,使得△ABC与△ABP的面积相等?请直接写出点P的坐标.
22.如图,直线y=kx+b经过点A(0,5),B(1,4).
(1)求直线AB的解析式;
(2)若直线y=2x﹣4与直线AB相交于点C,求点C的坐标;
(3)根据图象,写出关于x的不等式2x﹣4≥kx+b的解集.
AACBBAAAAD
﹣2<x<﹣1 . 大于4 . x< . x>﹣1 .x>1 . x<1 . ﹣4<x<﹣1 . x>﹣
19 x≥5.
20. 解:(1)当x=0时,x+3=0+3=3,
∴点A的坐标是(0,3),
∵点A与点B恰好关于x轴对称,
∴B点坐标为(0,﹣3);
(2)∵点P横坐标为﹣1,
∴(﹣1)+3=,
∴点P的坐标是(﹣1,),
设直线l2的解析式为y=kx+b,
则,
解得,
∴直线l2的解析式为y=﹣x﹣3;
(3)∵点P横坐标是﹣1,△MAB的面积是△PAB的面积的,
∴点M的横坐标的长度是,
①当横坐标是﹣时,y=(﹣)×(﹣)﹣3=﹣3=﹣,
②当横坐标是时,y=(﹣)×﹣3=﹣﹣3=﹣,
∴M点的坐标是(﹣,﹣)或(,﹣);
(4)l1:y=x+3,当y=0时,x+3=0,解得x=﹣6,
l2:y=﹣x﹣3,当y=0时,﹣x﹣3=0,
解得x=﹣,
∴当﹣6<x<﹣时,l1、l2表示的两个函数的函数值都大于0.
21 解:(1)由直线l1的解析式为y1=x+1,可求得C(0,1);
则依题意可得:,
解得:.(2)由(1)知,直线l2:y=﹣x+1;
∵y1=x+1>0,∴x>﹣1;
∵;
∴﹣1<x<2.
(3)由题意知A(﹣1,0),则AB=3,且OC=1;
∴S△ABC=AB OC=.
(4)由于△ABC、△ABP同底,若面积相等,则P点纵坐标为﹣1,代入直线l1可求得:
P的坐标为(﹣2,﹣1).
22. 解:(1)∵直线y=﹣kx+b经过点A(5,0)、B(1,4),
∴,
解方程组得,
∴直线AB的解析式为y=﹣x+5;
(2)∵直线y=2x﹣4与直线AB相交于点C,
∴解方程组,
解得,
∴点C的坐标为(3,2);(3)由图可知,x≥3时,2x﹣4≥kx+b.
