北师大版八年级数学上册 第六章 数据的分析 复习课件(共21张PPT)
文档属性
| 名称 | 北师大版八年级数学上册 第六章 数据的分析 复习课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 375.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-28 14:08:11 | ||
图片预览






文档简介
(共21张PPT)
复习课件
第六章 数据的分析
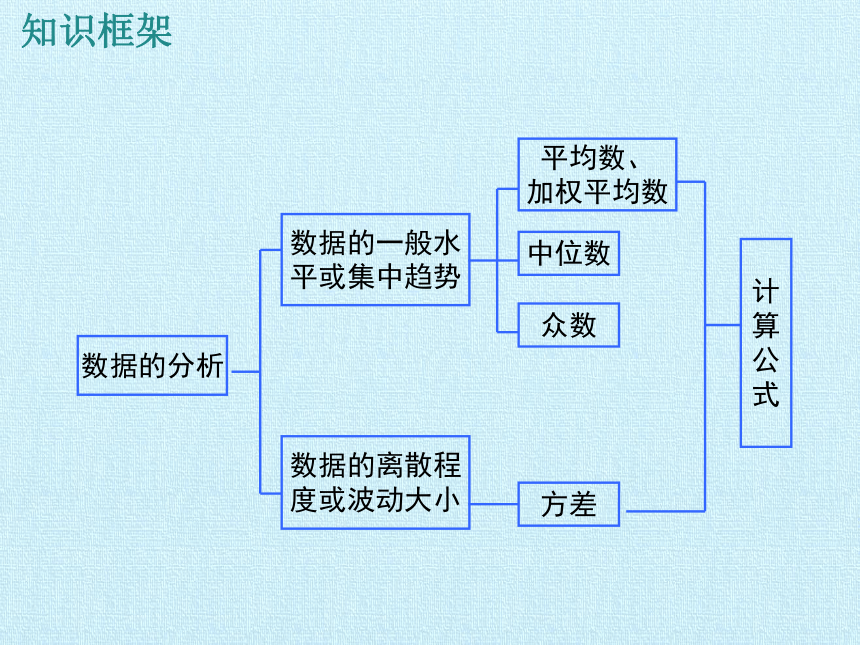
数据的分析
数据的一般水
平或集中趋势
数据的离散程
度或波动大小
平均数、
加权平均数
中位数
众数
方差
计
算
公
式
知识框架
数据的代表
一
平均数 定义 一组数据的平均值称为这组数据的平均数
算术平 均数 一般地,如果有n个数x1,x2,…,xn,那么
叫做这n个数的平均数
加权平 均数 一般地,如果在n个数x1,x2,…,xn中,x1出现f1次,x2出现f2次,…,xk出现fk次(其中f1+f2+…+fk=n),那么,
叫做x1,x2,…,xk这k个数的加权平均数,其中f1,f2,…,fk叫做x1,x2,…,xk的权,f1+f2+…+fk=n
知识梳理
最多
中间位置的数
两个数据的平均数
中位数 定义 将一组数据按照由小到大(或由大到小)的顺序排列,如果数据的个数是奇数,则处于________________就是这组数据的中位数,如果数据的个数是偶数,则中间_________________________就是这组数据的中位数
防错 提醒 确定中位数时,一定要注意先把整组数据按照大小顺序排列,再确定
众 数 定义 一组数据中出现次数________的数据叫做这组数据的众数
防错 提醒 (1)一组数据中众数不一定只有一个;(2)当一组数据中出现异常值时,其平均数往往不能正确反映这组数据的集中趋势,就应考虑用中位数或众数来分析
(2)条形统计图中,
(3)扇形统计图中,
(1)折线统计图中,
众数:同一水平线上出现次数最多的数据;
中位数:从上到下(或从下到上)找中间点所对的数;
平均数:可以用中位数与众数估测平均数.
众数:是柱子最高的数据;
中位数:从左到右(或从右到左)找中间数;
平均数:可以用中位数与众数估测平均数.
众数:为扇形面积最大的数据;
中位数:按顺序,看相应百分比,第50%与51%两个数据的平均数;
平均数:可以利用加权平均数进行计算.
从统计图中分析数据
二
数据的波动
三
平均数
大
表示波 动的量 定义 意义
方差 设有n个数据x1,x2,x3,…,xn,各数据与它们的______的差的平方分别是(x1-x)2,(x2-x)2,…,(xn-x)2,我们用它们的平均数,即用_____________________________来衡量这组数据的波动大小,并把它叫做这组数据的方差,记作s2 方差越大,数据的波动越________,反之也成立
标准差就是方差的算术平方根
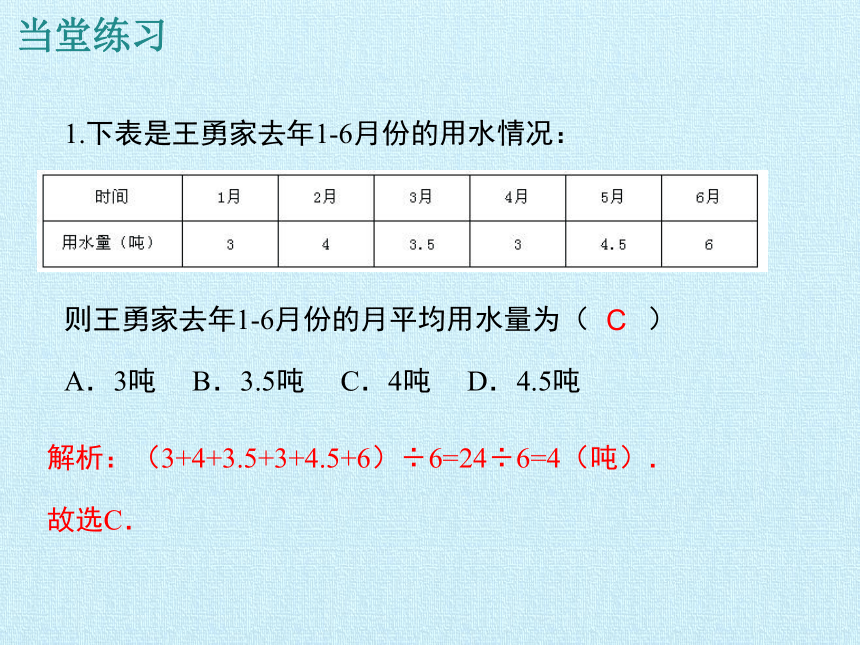
1.下表是王勇家去年1-6月份的用水情况:
则王勇家去年1-6月份的月平均用水量为( )
A.3吨 B.3.5吨 C.4吨 D.4.5吨
C
当堂练习
解析:(3+4+3.5+3+4.5+6)÷6=24÷6=4(吨).
故选C.
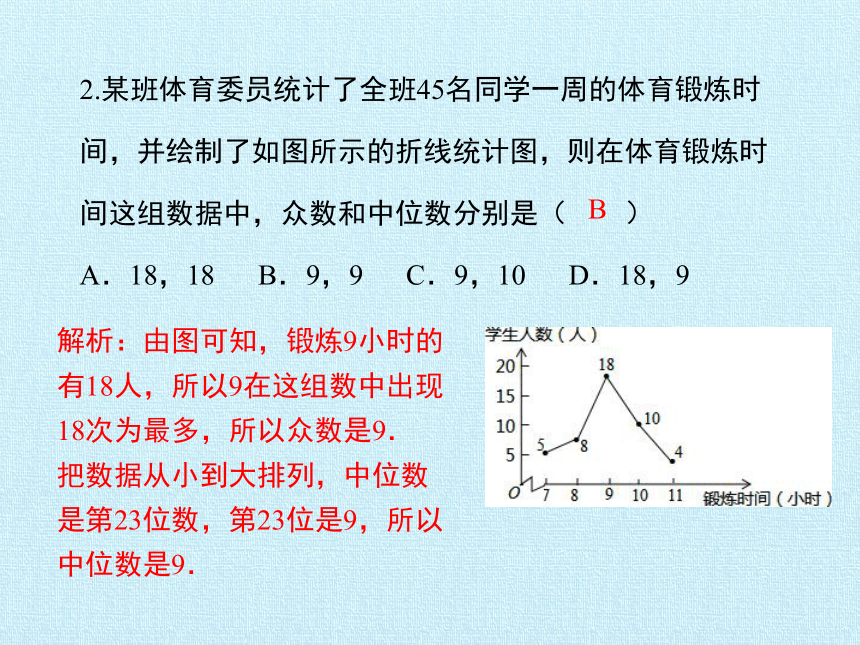
2.某班体育委员统计了全班45名同学一周的体育锻炼时间,并绘制了如图所示的折线统计图,则在体育锻炼时间这组数据中,众数和中位数分别是( )
A.18,18 B.9,9 C.9,10 D.18,9
B
解析:由图可知,锻炼9小时的有18人,所以9在这组数中出现18次为最多,所以众数是9.
把数据从小到大排列,中位数是第23位数,第23位是9,所以中位数是9.
3.要反映台州市某一周每天的最高气温的变化趋势,宜采用( )
A.条形统计图 B.扇形统计图
C.折线统计图 D.频数分布直方图
C
4.如图是某农户2015年收入情况的扇形统计图,已知他2015年的总收入为5万元,则他的打工收入是( )
A.0.75万元 B.1.25万元
C.1.75万元 D.2万元
B
解析:5万元×25%=1.25万元.
5. 我市某中学七、八年级各选派10名选手参加学校举办的“爱我荆门”知识竞赛,计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀.这次竞赛后,七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表如下所示,其中七年级代表队得6分、10分的选手人数分别为a,b.
队别 平均分 中位数 方差 合格率 优秀率
七年级 6.7 m 3.41 90% n
八年级 7.1 7.5 1.69 80% 10%
(1)请依据图表中的数据,求a,b的值;
(2)直接写出表中m,n的值;
(3)有人说七年级的合格率、优秀率均高于八年级,所以七年级队成绩比八年级队好,但也有人说八年级队成绩比七年级队好.请你给出两条支持八年级队成绩好的理由.
(1)解:依题意,得
解得
3×1+6a+7×1+8×1+9×1+10b=6.7×10
a+1+1+1+b=90%×10或1+a+1+1+1+b=10
a=5
b=1
(1)请依据图表中的数据,求a,b的值;
(2)m=6,n=20%.
(2)直接写出表中m,n的值;
队别 平均分 中位数 方差 合格率 优秀率
七年级 6.7 m 3.41 90% n
八年级 7.1 7.5 1.69 80% 10%
(3)①八年级队平均分高于七年级队;②八年级队的成绩比七年级队稳定;③八年级队的成绩集中在中上游,所以支持八年级队成绩好.(注:任说两条即可)
(3)有人说七年级的合格率、优秀率均高于八年级,
所以七年级队成绩比八年级队好,但也有人说八
年级队成绩比七年级队好.请你给出两条支持八
年级队成绩好的理由.
6.为了从甲、乙两名选手中选拔一个参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了如下统计图表:
甲、乙射击成绩统计表
平均数 中位数 方差 命中10环的次数
甲 7 0
乙 1
甲、乙射击成绩折线图
(1)请补全上述图表(请直接在表中填空和补全折线图);
(2)如果规定成绩较稳定者胜出,你认为谁应胜出?说明你的理由;
(3)如果希望(2)中的另一名选手胜出,根据图表中的信息,应该制定怎样的评判规则?为什么?
解:(1)根据折线统计图,得乙的射击成绩为2,4,6,8,7,7,8,9,9,10,
平均数为 (环)
中位数为7.5环,
方差为 [(2-7)2+(4-7)2+(6-7)2+(8-7)2+(7-7)2+(7-7)2+(8-7)2+(9-7)2+(9-7)2+(10-7)2]=5.4.
根据折线统计图,知甲除第八次外的射击成绩为9,6,7,6,2,7,7,8,9,平均数为7,
则甲第八次成绩为70-(9+6+7+6+2+7+7+8+9)=9(环),所以甲的射击成绩为2,6,6,7,7,7,8,9,9,9,
中位数为7环,平均数为(2+6+6+7+7+7+8+9+9+9)=7(环),
方差为[(2-7)2+(6-7)2+(6-7)2+(7-7)2+(7-7)2+(7-7)2+(8-7)2+(9-7)2+(9-7)2+(9-7)2]=4.
补全图表如下.
甲、乙射击成绩统计表
平均数 中位数 方差 命中10环的次数
甲 7 7 4 0
乙 7 7.5 5.4 1
甲、乙射击成绩折线图
(2)甲胜出.理由:因为甲的方差小于乙的方差.
(3)略.
谢 谢
复习课件
第六章 数据的分析
数据的分析
数据的一般水
平或集中趋势
数据的离散程
度或波动大小
平均数、
加权平均数
中位数
众数
方差
计
算
公
式
知识框架
数据的代表
一
平均数 定义 一组数据的平均值称为这组数据的平均数
算术平 均数 一般地,如果有n个数x1,x2,…,xn,那么
叫做这n个数的平均数
加权平 均数 一般地,如果在n个数x1,x2,…,xn中,x1出现f1次,x2出现f2次,…,xk出现fk次(其中f1+f2+…+fk=n),那么,
叫做x1,x2,…,xk这k个数的加权平均数,其中f1,f2,…,fk叫做x1,x2,…,xk的权,f1+f2+…+fk=n
知识梳理
最多
中间位置的数
两个数据的平均数
中位数 定义 将一组数据按照由小到大(或由大到小)的顺序排列,如果数据的个数是奇数,则处于________________就是这组数据的中位数,如果数据的个数是偶数,则中间_________________________就是这组数据的中位数
防错 提醒 确定中位数时,一定要注意先把整组数据按照大小顺序排列,再确定
众 数 定义 一组数据中出现次数________的数据叫做这组数据的众数
防错 提醒 (1)一组数据中众数不一定只有一个;(2)当一组数据中出现异常值时,其平均数往往不能正确反映这组数据的集中趋势,就应考虑用中位数或众数来分析
(2)条形统计图中,
(3)扇形统计图中,
(1)折线统计图中,
众数:同一水平线上出现次数最多的数据;
中位数:从上到下(或从下到上)找中间点所对的数;
平均数:可以用中位数与众数估测平均数.
众数:是柱子最高的数据;
中位数:从左到右(或从右到左)找中间数;
平均数:可以用中位数与众数估测平均数.
众数:为扇形面积最大的数据;
中位数:按顺序,看相应百分比,第50%与51%两个数据的平均数;
平均数:可以利用加权平均数进行计算.
从统计图中分析数据
二
数据的波动
三
平均数
大
表示波 动的量 定义 意义
方差 设有n个数据x1,x2,x3,…,xn,各数据与它们的______的差的平方分别是(x1-x)2,(x2-x)2,…,(xn-x)2,我们用它们的平均数,即用_____________________________来衡量这组数据的波动大小,并把它叫做这组数据的方差,记作s2 方差越大,数据的波动越________,反之也成立
标准差就是方差的算术平方根
1.下表是王勇家去年1-6月份的用水情况:
则王勇家去年1-6月份的月平均用水量为( )
A.3吨 B.3.5吨 C.4吨 D.4.5吨
C
当堂练习
解析:(3+4+3.5+3+4.5+6)÷6=24÷6=4(吨).
故选C.
2.某班体育委员统计了全班45名同学一周的体育锻炼时间,并绘制了如图所示的折线统计图,则在体育锻炼时间这组数据中,众数和中位数分别是( )
A.18,18 B.9,9 C.9,10 D.18,9
B
解析:由图可知,锻炼9小时的有18人,所以9在这组数中出现18次为最多,所以众数是9.
把数据从小到大排列,中位数是第23位数,第23位是9,所以中位数是9.
3.要反映台州市某一周每天的最高气温的变化趋势,宜采用( )
A.条形统计图 B.扇形统计图
C.折线统计图 D.频数分布直方图
C
4.如图是某农户2015年收入情况的扇形统计图,已知他2015年的总收入为5万元,则他的打工收入是( )
A.0.75万元 B.1.25万元
C.1.75万元 D.2万元
B
解析:5万元×25%=1.25万元.
5. 我市某中学七、八年级各选派10名选手参加学校举办的“爱我荆门”知识竞赛,计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀.这次竞赛后,七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表如下所示,其中七年级代表队得6分、10分的选手人数分别为a,b.
队别 平均分 中位数 方差 合格率 优秀率
七年级 6.7 m 3.41 90% n
八年级 7.1 7.5 1.69 80% 10%
(1)请依据图表中的数据,求a,b的值;
(2)直接写出表中m,n的值;
(3)有人说七年级的合格率、优秀率均高于八年级,所以七年级队成绩比八年级队好,但也有人说八年级队成绩比七年级队好.请你给出两条支持八年级队成绩好的理由.
(1)解:依题意,得
解得
3×1+6a+7×1+8×1+9×1+10b=6.7×10
a+1+1+1+b=90%×10或1+a+1+1+1+b=10
a=5
b=1
(1)请依据图表中的数据,求a,b的值;
(2)m=6,n=20%.
(2)直接写出表中m,n的值;
队别 平均分 中位数 方差 合格率 优秀率
七年级 6.7 m 3.41 90% n
八年级 7.1 7.5 1.69 80% 10%
(3)①八年级队平均分高于七年级队;②八年级队的成绩比七年级队稳定;③八年级队的成绩集中在中上游,所以支持八年级队成绩好.(注:任说两条即可)
(3)有人说七年级的合格率、优秀率均高于八年级,
所以七年级队成绩比八年级队好,但也有人说八
年级队成绩比七年级队好.请你给出两条支持八
年级队成绩好的理由.
6.为了从甲、乙两名选手中选拔一个参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了如下统计图表:
甲、乙射击成绩统计表
平均数 中位数 方差 命中10环的次数
甲 7 0
乙 1
甲、乙射击成绩折线图
(1)请补全上述图表(请直接在表中填空和补全折线图);
(2)如果规定成绩较稳定者胜出,你认为谁应胜出?说明你的理由;
(3)如果希望(2)中的另一名选手胜出,根据图表中的信息,应该制定怎样的评判规则?为什么?
解:(1)根据折线统计图,得乙的射击成绩为2,4,6,8,7,7,8,9,9,10,
平均数为 (环)
中位数为7.5环,
方差为 [(2-7)2+(4-7)2+(6-7)2+(8-7)2+(7-7)2+(7-7)2+(8-7)2+(9-7)2+(9-7)2+(10-7)2]=5.4.
根据折线统计图,知甲除第八次外的射击成绩为9,6,7,6,2,7,7,8,9,平均数为7,
则甲第八次成绩为70-(9+6+7+6+2+7+7+8+9)=9(环),所以甲的射击成绩为2,6,6,7,7,7,8,9,9,9,
中位数为7环,平均数为(2+6+6+7+7+7+8+9+9+9)=7(环),
方差为[(2-7)2+(6-7)2+(6-7)2+(7-7)2+(7-7)2+(7-7)2+(8-7)2+(9-7)2+(9-7)2+(9-7)2]=4.
补全图表如下.
甲、乙射击成绩统计表
平均数 中位数 方差 命中10环的次数
甲 7 7 4 0
乙 7 7.5 5.4 1
甲、乙射击成绩折线图
(2)甲胜出.理由:因为甲的方差小于乙的方差.
(3)略.
谢 谢
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
