五年级上册数学单元测试 7.解决问题的策略 苏教版(含答案)
文档属性
| 名称 | 五年级上册数学单元测试 7.解决问题的策略 苏教版(含答案) | 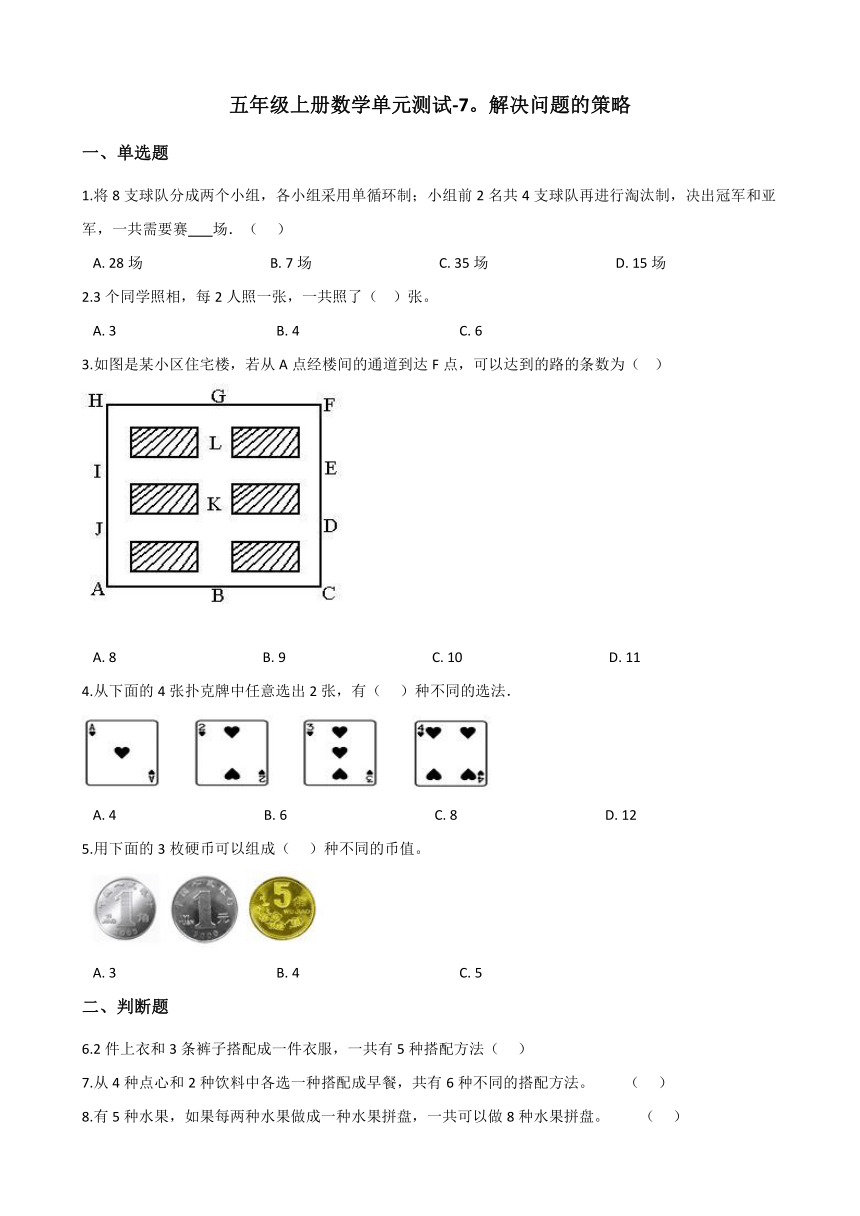 | |
| 格式 | docx | ||
| 文件大小 | 108.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-27 11:42:45 | ||
图片预览



文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
五年级上册数学单元测试-7。解决问题的策略
一、单选题
1.将8支球队分成两个小组,各小组采用单循环制;小组前2名共4支球队再进行淘汰制,决出冠军和亚军,一共需要赛 场.( )
A. 28场 B. 7场 C. 35场 D. 15场
2.3个同学照相,每2人照一张,一共照了( )张。
A. 3 B. 4 C. 6
3.如图是某小区住宅楼,若从A点经楼间的通道到达F点,可以达到的路的条数为( )
A. 8 B. 9 C. 10 D. 11
4.从下面的4张扑克牌中任意选出2张,有( )种不同的选法.
A. 4 B. 6 C. 8 D. 12
5.用下面的3枚硬币可以组成( )种不同的币值。
A. 3 B. 4 C. 5
二、判断题
6.2件上衣和3条裤子搭配成一件衣服,一共有5种搭配方法( )
7.从4种点心和2种饮料中各选一种搭配成早餐,共有6种不同的搭配方法。 ( )
8.有5种水果,如果每两种水果做成一种水果拼盘,一共可以做8种水果拼盘。 ( )
三、填空题
9.小红、小云、小明、小菊4人进行乒乓球比赛,每2人赛一场,一共要赛________场。
10.28,24,20,16,12,________,________。
11.把120个苹果分成若干堆(不止一堆),每堆苹果一样多,并且均为双数,共有________种方法。
四、解答题
12.四个人见面,每两人互相握手问好,一共要握几次手?
13.由 个不同的独唱节目和 个不同的合唱节目组成一台晚会,要求任意两个合唱节目不相邻,开始和最后一个节目必须是合唱,则这台晚会节目的编排方法共有多少种?(6级)
14.幼儿园里3名小朋友去坐6把不同的椅子(每人只能坐一把),有多少种不同的坐法?
15.a,b,c,d,e五个人排成一排,a与b不相邻,共有多少种不同的排法?
五、应用题
16.同学们就要过寒假了,分别时互相握手,每2个人握一次手,5人一共要握几次手?(可以画图来表示过程,并要求答.)
17.老张、老王、老李、老赵是好朋友,一天,他们四人碰面,每两人都握一次手,他们一共握了多少次手?(先画一画,再解答.)
参考答案
一、单选题
1.【答案】 D
【解析】【解答】解:单循环赛:8÷2=4(支)
3+2+1=6(场)
6×2=12(场)
淘汰赛:4÷2=2(场)
2÷2=1(场)
12+3=15(场)
故答案为:15.
【分析】用8除以2求出每组球队的支数,再求出每组进行单循环赛的场次,然后乘2求出单循环赛的场次;因为淘汰赛每场都要淘汰一半的球队,所以直接用球队的支数依次除以2求出淘汰赛的场次,再加上单循环赛的场次即可。
2.【答案】 A
【解析】【解答】解:2+1=3(张)
故答案为:A。
【分析】甲乙丙3人照相,每2人照一张,即甲乙照一张,甲丙照一张,乙丙照一张,其和就是一共照的张数。
3.【答案】 C
【解析】【解答】ABKDEF、ABLEF、ABGF、ABCF、AJKDF、AJKLEF、AJKLGF、AILEF、AILGF、AHGF,共10条路.
故答案为:C
【分析】从A到F,有多个楼间通道,只可以向右,向上走,把所有的路线都列举出来即可.
4.【答案】 B
【解析】【解答】解:假设其中一张是A,则有A2、A3、A4共3种组合;再假设其中一张是2,则有23、24共2种组合(2A在第一种情况中已有);再假设其中一张是3,则有34共1种组合(3A、32在第一、二种情况中已有);若其中一张是4,与其它的组合都已存在。所以在不同的4张扑克牌中任意选出2张,有3+2+1=6种不同的选法。
故答案为:B。
【分析】先固定一张卡片,去变换另一张卡片,得到不同的选法;再将固定的卡片换一张,继续变换另一种卡片,依次改变最后将所有的选法加起来即可,需注意重复选法只计算一次。
5.【答案】 B
【解析】【解答】 用下面的3枚硬币可以组成4种不同的币值。
故答案为:B。
【分析】可以看看两枚、三枚组合各组成多少种币值,然后相加即可。
二、判断题
6.【答案】 正确
【解析】【解答】解:一共有2×3=6种搭配方法。
故答案为:正确。
【分析】一件上衣有3种搭配裤子的方法,那么2件上衣就有2×3=6种搭配方法。
7.【答案】 错误
【解析】【解答】解:4×2=8(种),所以从4种点心和2种饮料中各选一种搭配成早餐,共有8种不同的搭配方法。
故答案为:错误。
【分析】先选择点心有4种选法,再选择饮料有2种选法,一共有4×2种不同的搭配方法。
8.【答案】 错误
【解析】【解答】解:5×4÷2
=20÷2
=10(种),
所以一共可以做10种水果拼盘。
故答案为:错误。
【分析】本题相当于握手问题,若有n个人,则一个人握手(n-1)次,则n个人握手n(n-1)次,但是甲与乙握手和乙与甲握手应该算作一次,所以握手总次数为n(n-1)÷2次,本题即是根据握手总次数的公式进行求解的。
三、填空题
9.【答案】 6
【解析】【解答】小红与小云、小明、小菊各进行1场比赛;小云与小明、小菊各进行1场比赛;小明与小菊进行1场比赛,则一共进行6场比赛。
故答案为:6
【分析】首先明确每人最多进行3场比赛,再根据排列组合进行相互组合,即可得出答案。
10.【答案】 8;4
【解析】
11.【答案】 11
【解析】【解答】 把120个苹果分成若干堆(不止一堆),每堆苹果一样多,并且均为双数,共有11种方法。
故答案为:11。
【分析】120=2×60=3×40=4×30=5×24=6×20=8×15=10×12=12×10=15×8=20×6=30×4=40×3=60×2
把120分解成两个整数因数的积,其中第一个因数表示堆数,第二个因数表示每堆个数,共13中组合,根据题意,把其中第二个因数为单数的2种组合去掉,共11分法。
四、解答题
12.【答案】 解:4×3÷2
=12÷2
=6(次)
答:一共要握6次手。
【解析】【分析】4个小朋友每两人握手依次,则每个小朋友都要和其他3个人握一次手,即每个人要握3次手,共有4个小朋友,所以共握3×4次,握手是在两个人之间进行的,所以他们握手的次数需要除以2。
13.【答案】 解:先排独唱节目,四个节目随意排,是 个元素全排列的问题,有 种排法;其次在独唱节目的首尾排合唱节目,有三个节目,两个位置,也就是从三个节目选两个进行排列的问题,有 (种)排法;再在独唱节目之间的 个位置中排一个合唱节目,有 种排法.由乘法原理,一共有 (种)不同的编排方法.
【解析】【分析】第一步:对4个独唱节目进行全排列;第二步:排首尾的合唱节目;第三步:在独唱节目之间插空。最后把每一步的排法乘起来即可。
14.【答案】 解:与例 不同,这次是椅子多而人少,可以考虑把 把椅子看成是 个元素,而把 名小朋友作为 个位置,则问题转化为从 把椅子中选出 把,排在 名小朋友面前的排列问题.
由排列公式,共有: (种)不同的坐法.
【解析】【分析】本题可以看成是从6把椅子中选出3把,排在3名小朋友面前的排列问题。
15.【答案】 解:解法一:插空法,先排 , , ,有 种排法.
在 , , 三个人之间有2个空,再加上两端,共有4个空, , 排在这4个空的位置上, 与 就不相邻,有 种排法.
根据分步计数乘法原理,不同的排法共有(种).
解法二:排除法,把 , 当作一个人和其他三个人在一起排列,再考虑 与 本身的顺序,有 种排法.
总的排法为 .
总的排法减去 与 相邻的排法即为 与 不相邻的排法,应为 (种).
【解析】【分析】方法一(插空法):第一步:排c,d,e;第二步:将a,b分别插入c,d,e之间的两个空。最后把两步的排法乘起来即可;
方法二(排除法):将a,b当作一个人和其他三个人在一起排列,再考虑a,b本身的顺序,总排法就是把五个人进行全排列,那么a,b不相邻的排法数=总排法-将a,b当作一个人的排法。
五、应用题
16.【答案】 解:假设5个人分别是A、B、C、D、E,互相握手情况如下图:
(5﹣1)×5÷2
=20÷2
=10(次);
答:5人一共要握10次手.
【解析】【分析】每个人都要和另外的4个人握一次手,5个人共握4×5=20次,由于每两人握手,应算作一次手,去掉重复的情况,实际只握了20÷2=10次,据此解答.
17.【答案】 解:
(4﹣1)×4÷2
=12÷2
=6(次)
答:他们一共握了6次手.
【解析】【分析】由于每个人都要和另外的3个人握一次手,一共要握:4×3=12(次);又因为两个人只握一次,去掉重复计算的情况,实际只握:12÷2=6(次),据此解答.
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
五年级上册数学单元测试-7。解决问题的策略
一、单选题
1.将8支球队分成两个小组,各小组采用单循环制;小组前2名共4支球队再进行淘汰制,决出冠军和亚军,一共需要赛 场.( )
A. 28场 B. 7场 C. 35场 D. 15场
2.3个同学照相,每2人照一张,一共照了( )张。
A. 3 B. 4 C. 6
3.如图是某小区住宅楼,若从A点经楼间的通道到达F点,可以达到的路的条数为( )
A. 8 B. 9 C. 10 D. 11
4.从下面的4张扑克牌中任意选出2张,有( )种不同的选法.
A. 4 B. 6 C. 8 D. 12
5.用下面的3枚硬币可以组成( )种不同的币值。
A. 3 B. 4 C. 5
二、判断题
6.2件上衣和3条裤子搭配成一件衣服,一共有5种搭配方法( )
7.从4种点心和2种饮料中各选一种搭配成早餐,共有6种不同的搭配方法。 ( )
8.有5种水果,如果每两种水果做成一种水果拼盘,一共可以做8种水果拼盘。 ( )
三、填空题
9.小红、小云、小明、小菊4人进行乒乓球比赛,每2人赛一场,一共要赛________场。
10.28,24,20,16,12,________,________。
11.把120个苹果分成若干堆(不止一堆),每堆苹果一样多,并且均为双数,共有________种方法。
四、解答题
12.四个人见面,每两人互相握手问好,一共要握几次手?
13.由 个不同的独唱节目和 个不同的合唱节目组成一台晚会,要求任意两个合唱节目不相邻,开始和最后一个节目必须是合唱,则这台晚会节目的编排方法共有多少种?(6级)
14.幼儿园里3名小朋友去坐6把不同的椅子(每人只能坐一把),有多少种不同的坐法?
15.a,b,c,d,e五个人排成一排,a与b不相邻,共有多少种不同的排法?
五、应用题
16.同学们就要过寒假了,分别时互相握手,每2个人握一次手,5人一共要握几次手?(可以画图来表示过程,并要求答.)
17.老张、老王、老李、老赵是好朋友,一天,他们四人碰面,每两人都握一次手,他们一共握了多少次手?(先画一画,再解答.)
参考答案
一、单选题
1.【答案】 D
【解析】【解答】解:单循环赛:8÷2=4(支)
3+2+1=6(场)
6×2=12(场)
淘汰赛:4÷2=2(场)
2÷2=1(场)
12+3=15(场)
故答案为:15.
【分析】用8除以2求出每组球队的支数,再求出每组进行单循环赛的场次,然后乘2求出单循环赛的场次;因为淘汰赛每场都要淘汰一半的球队,所以直接用球队的支数依次除以2求出淘汰赛的场次,再加上单循环赛的场次即可。
2.【答案】 A
【解析】【解答】解:2+1=3(张)
故答案为:A。
【分析】甲乙丙3人照相,每2人照一张,即甲乙照一张,甲丙照一张,乙丙照一张,其和就是一共照的张数。
3.【答案】 C
【解析】【解答】ABKDEF、ABLEF、ABGF、ABCF、AJKDF、AJKLEF、AJKLGF、AILEF、AILGF、AHGF,共10条路.
故答案为:C
【分析】从A到F,有多个楼间通道,只可以向右,向上走,把所有的路线都列举出来即可.
4.【答案】 B
【解析】【解答】解:假设其中一张是A,则有A2、A3、A4共3种组合;再假设其中一张是2,则有23、24共2种组合(2A在第一种情况中已有);再假设其中一张是3,则有34共1种组合(3A、32在第一、二种情况中已有);若其中一张是4,与其它的组合都已存在。所以在不同的4张扑克牌中任意选出2张,有3+2+1=6种不同的选法。
故答案为:B。
【分析】先固定一张卡片,去变换另一张卡片,得到不同的选法;再将固定的卡片换一张,继续变换另一种卡片,依次改变最后将所有的选法加起来即可,需注意重复选法只计算一次。
5.【答案】 B
【解析】【解答】 用下面的3枚硬币可以组成4种不同的币值。
故答案为:B。
【分析】可以看看两枚、三枚组合各组成多少种币值,然后相加即可。
二、判断题
6.【答案】 正确
【解析】【解答】解:一共有2×3=6种搭配方法。
故答案为:正确。
【分析】一件上衣有3种搭配裤子的方法,那么2件上衣就有2×3=6种搭配方法。
7.【答案】 错误
【解析】【解答】解:4×2=8(种),所以从4种点心和2种饮料中各选一种搭配成早餐,共有8种不同的搭配方法。
故答案为:错误。
【分析】先选择点心有4种选法,再选择饮料有2种选法,一共有4×2种不同的搭配方法。
8.【答案】 错误
【解析】【解答】解:5×4÷2
=20÷2
=10(种),
所以一共可以做10种水果拼盘。
故答案为:错误。
【分析】本题相当于握手问题,若有n个人,则一个人握手(n-1)次,则n个人握手n(n-1)次,但是甲与乙握手和乙与甲握手应该算作一次,所以握手总次数为n(n-1)÷2次,本题即是根据握手总次数的公式进行求解的。
三、填空题
9.【答案】 6
【解析】【解答】小红与小云、小明、小菊各进行1场比赛;小云与小明、小菊各进行1场比赛;小明与小菊进行1场比赛,则一共进行6场比赛。
故答案为:6
【分析】首先明确每人最多进行3场比赛,再根据排列组合进行相互组合,即可得出答案。
10.【答案】 8;4
【解析】
11.【答案】 11
【解析】【解答】 把120个苹果分成若干堆(不止一堆),每堆苹果一样多,并且均为双数,共有11种方法。
故答案为:11。
【分析】120=2×60=3×40=4×30=5×24=6×20=8×15=10×12=12×10=15×8=20×6=30×4=40×3=60×2
把120分解成两个整数因数的积,其中第一个因数表示堆数,第二个因数表示每堆个数,共13中组合,根据题意,把其中第二个因数为单数的2种组合去掉,共11分法。
四、解答题
12.【答案】 解:4×3÷2
=12÷2
=6(次)
答:一共要握6次手。
【解析】【分析】4个小朋友每两人握手依次,则每个小朋友都要和其他3个人握一次手,即每个人要握3次手,共有4个小朋友,所以共握3×4次,握手是在两个人之间进行的,所以他们握手的次数需要除以2。
13.【答案】 解:先排独唱节目,四个节目随意排,是 个元素全排列的问题,有 种排法;其次在独唱节目的首尾排合唱节目,有三个节目,两个位置,也就是从三个节目选两个进行排列的问题,有 (种)排法;再在独唱节目之间的 个位置中排一个合唱节目,有 种排法.由乘法原理,一共有 (种)不同的编排方法.
【解析】【分析】第一步:对4个独唱节目进行全排列;第二步:排首尾的合唱节目;第三步:在独唱节目之间插空。最后把每一步的排法乘起来即可。
14.【答案】 解:与例 不同,这次是椅子多而人少,可以考虑把 把椅子看成是 个元素,而把 名小朋友作为 个位置,则问题转化为从 把椅子中选出 把,排在 名小朋友面前的排列问题.
由排列公式,共有: (种)不同的坐法.
【解析】【分析】本题可以看成是从6把椅子中选出3把,排在3名小朋友面前的排列问题。
15.【答案】 解:解法一:插空法,先排 , , ,有 种排法.
在 , , 三个人之间有2个空,再加上两端,共有4个空, , 排在这4个空的位置上, 与 就不相邻,有 种排法.
根据分步计数乘法原理,不同的排法共有(种).
解法二:排除法,把 , 当作一个人和其他三个人在一起排列,再考虑 与 本身的顺序,有 种排法.
总的排法为 .
总的排法减去 与 相邻的排法即为 与 不相邻的排法,应为 (种).
【解析】【分析】方法一(插空法):第一步:排c,d,e;第二步:将a,b分别插入c,d,e之间的两个空。最后把两步的排法乘起来即可;
方法二(排除法):将a,b当作一个人和其他三个人在一起排列,再考虑a,b本身的顺序,总排法就是把五个人进行全排列,那么a,b不相邻的排法数=总排法-将a,b当作一个人的排法。
五、应用题
16.【答案】 解:假设5个人分别是A、B、C、D、E,互相握手情况如下图:
(5﹣1)×5÷2
=20÷2
=10(次);
答:5人一共要握10次手.
【解析】【分析】每个人都要和另外的4个人握一次手,5个人共握4×5=20次,由于每两人握手,应算作一次手,去掉重复的情况,实际只握了20÷2=10次,据此解答.
17.【答案】 解:
(4﹣1)×4÷2
=12÷2
=6(次)
答:他们一共握了6次手.
【解析】【分析】由于每个人都要和另外的3个人握一次手,一共要握:4×3=12(次);又因为两个人只握一次,去掉重复计算的情况,实际只握:12÷2=6(次),据此解答.
