2021-2022学年九年级数学下册人教版26.2实际问题与反比例函数基础测试卷(word版、含答案)
文档属性
| 名称 | 2021-2022学年九年级数学下册人教版26.2实际问题与反比例函数基础测试卷(word版、含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 263.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-29 08:05:39 | ||
图片预览



文档简介
26.2实际问题与反比例函数基础测试卷
一、单选题(45分)
1.某气球充满一定质量的气体后,当温度不变时,气球内的气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示,当气球内的气压大于140kPa时,气球将爆炸,为了安全起见,气体体积应( )
A.不大于m3 B.不小于m3 C.不大于m3 D.不小于m3
2.点A(x1,y1),B(x2,y2)都在反比例函数的图象上,若x1<x2<0,则( )
A.y2>y1>0 B.y1>y2>0 C.y2<y1<0 D.y1<y2<0
3.某厂现有300吨煤,这些煤能烧的天数y与平均每天烧的吨数x之间的函数关系是( )
A.(x>0) B.(x≥0)
C.y=300x(x≥0) D.y=300x(x>0)
4.面积是160平方米的长方形,它的长y米,宽x米之间的关系表达式是( )
A.y=160x B.y= C.y=160+x D.y=160﹣x
5.某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种蔬菜.上图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图像,其中BC段是双曲线(k≠0)的一部分,则当x = 16时,大棚内的温度约为( )
A.18℃ B.15.5℃ C.13.5℃ D.12℃
6.已知力F对一个物体作的功是25焦,则力F与此物体在力在方向上移动的距离S之间的函数关系式的图象大致是( )
A.B.C.D.
7.甲、乙两地相距250千米,如果把汽车从甲地到乙地所用的时间y(小时),表示为汽车的平均速度为x(千米/小时)的函数,则此函数的图象大致是( ).
A. B. C.D.
8.已知一块蓄电池的电压为定值,以此蓄电池为电源时,电流I(A)与电阻R(Ω)之间的函数关系如图,则电流I关于电阻R的函数解析式为( )
A.I= B.I= C.I= D.I=-
9.如图,要围一个面积为20的矩形,若矩形的两邻边分别为、,则与的函数图象大致是( ).
A. B. C.D.
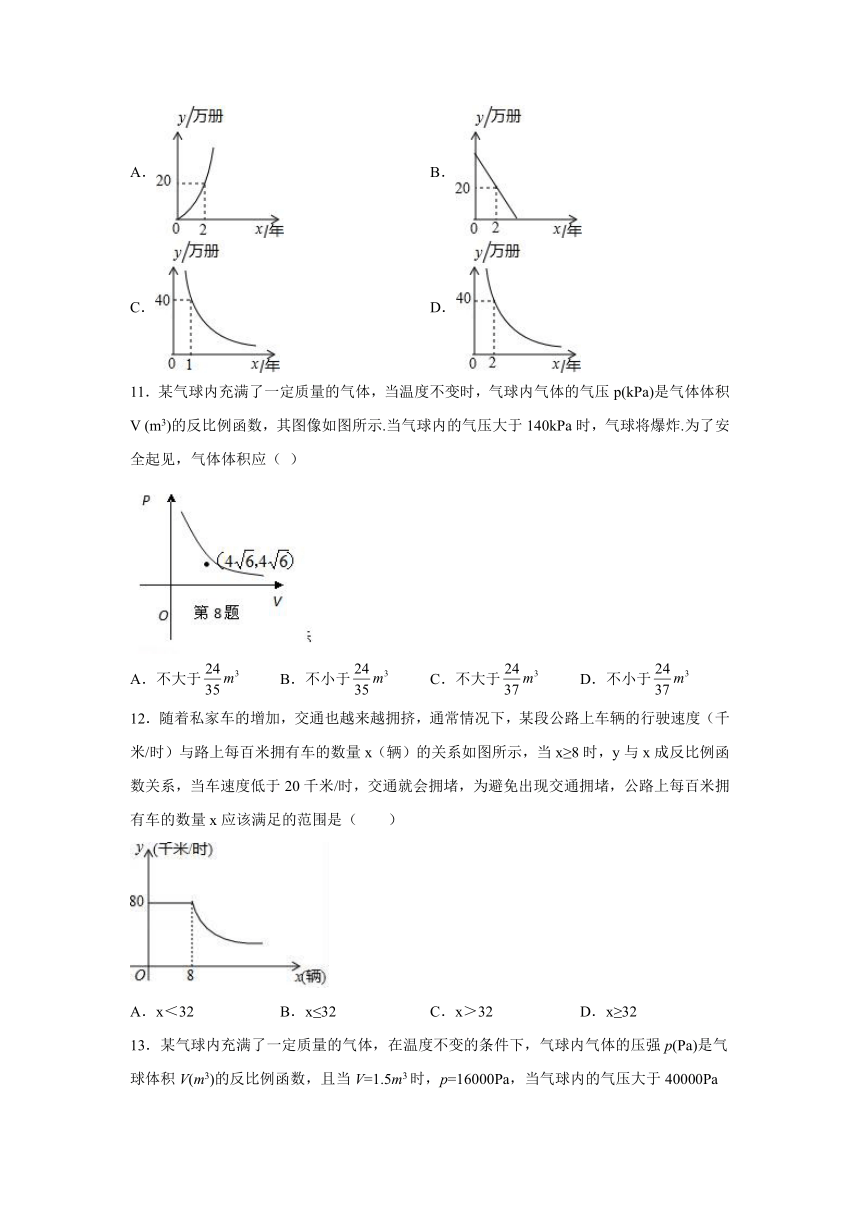
10.一台印刷机每年可印刷的书本数量y(万册)与它的使用时间x(年)成反比例关系,当x=2时,y=20.则y与x的函数图象大致是( )
A. B.
C. D.
11.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V (m3)的反比例函数,其图像如图所示.当气球内的气压大于140kPa时,气球将爆炸.为了安全起见,气体体积应( )
A.不大于 B.不小于 C.不大于 D.不小于
12.随着私家车的增加,交通也越来越拥挤,通常情况下,某段公路上车辆的行驶速度(千米/时)与路上每百米拥有车的数量x(辆)的关系如图所示,当x≥8时,y与x成反比例函数关系,当车速度低于20千米/时,交通就会拥堵,为避免出现交通拥堵,公路上每百米拥有车的数量x应该满足的范围是( )
A.x<32 B.x≤32 C.x>32 D.x≥32
13.某气球内充满了一定质量的气体,在温度不变的条件下,气球内气体的压强p(Pa)是气球体积V(m3)的反比例函数,且当V=1.5m3时,p=16000Pa,当气球内的气压大于40000Pa时,气球将爆炸,为确保气球不爆炸,气球的体积应( )
A.不小于0.5m3 B.不大于0.5m3 C.不小于0.6m3 D.不大于0.6m3
14.矩形面积为4,它的一边长y与邻边长x的函数关系用图象表示大致是( )
A.B.C.D.
15.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.则用电阻R表示电流I的函数表达式为( )
A. B. C. D.
二、填空题(15分)
16.一个水池装水12m3,如果从水管中每小时流出m3的水,经过h可以把水放完,那么 与的函数关系式是______,自变量的取值范围是______.
17.利用数学公式可建立反比例函数关系式,圆柱体的容积=_______×___.
18.一定质量的氧气,它的密度与它的体积V成反比例关系.当V=10m3时,=1.4kg/m3.则当=0.28kg/m3时,V=___.
19.学校内要设计一个面积是㎡长方形的运动场,则运动场的长与宽之间的函数关系式为________,当________时运动场是正方形.
20.一批零件600个,一个工人每小时做15个,用关系式表示人数x与完成任务所需的时间y之间的函数关系式为___________.
三、解答题(60分)
21.用洗衣粉洗衣物时,漂洗的次数与衣物中洗衣粉的残留量近似地满足反比例函数关系.某天,小金、小东放学回家后各自洗一件完全相同的衣服,漂洗时,小金每次用水约6升,小东每次用水约5升,他们都用了5克洗衣粉,第一次漂洗后,小金的衣服残留的洗衣粉还有1.5克,小东的衣服残留的洗衣粉还有2克.
(1)分别求出小金、小东衣服漂洗后洗衣粉残留量关于次数的函数解析式.
(2)已知洗衣粉的残留量降至0.35克时,便视为衣服漂洗干净,若以把衣服洗干净为前提,节约用水为目标,判断小金和小东两种漂洗方法用水量的大小,并说明理由.
22.如图,已知点A.B在双曲线y= (x>0)上,AC⊥x轴于C,BD⊥y轴于点D,AC与BD交于点P,P是AC的中点.
(1)设A的横坐标为m,试用m、k表示B的坐标.
(2)试判断四边形ABCD的形状,并说明理由.
(3)若△ABP的面积为3,求该双曲线的解析式.
23.为了预防“流感”,某学校对教室采用药熏法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(毫克/立方米)与药物点燃后的时间x(分钟)成正比例,药物燃尽后,y与x成反比例(如图所示).已知药物点燃后4分钟燃尽,此时室内每立方米空气中含药量为8毫克.
(1)求药物燃烧时,y与x之间函数的表达式;
(2)求药物燃尽后,y与x之间函数的表达式;
(3)研究表明,当空气中每立方米的含药量不低于2毫克时,才能有效杀灭空气中的病菌,那么此次消毒有效时间有多长?
参考答案
1--10BCABC BDCCC 11--15BBCAD
16. >0
17. 底面积 高
18.
19.
20.y=
21.(1)设小金衣服中洗衣粉的残留量与漂洗次数的函数关系式为:
则当
所以小金衣服中洗衣粉的残留量与漂洗次数的函数关系式为:
设小东衣服中洗衣粉的残留量与漂洗次数的函数关系式分别为:
则当
所以小东衣服中洗衣粉的残留量与漂洗次数的函数关系式分别为:
(2)把代入
可得:
可得洗衣的次数为5次,
所以小金用水升,
把代入
可得:
可得洗衣的次数为6次,
所以小东用水升,
所以小金的用水量与小东的用水量一样多.
22.(1)∵A的横坐标为m,AC⊥x轴于C,P是AC的中点,
∴点B的横坐标是2m.
又∵点B在双曲线y= (x>0)上,
∴B(2m,).
(2)连接AD、CD、BC;
∵AC⊥x轴于C,BD⊥y轴于点D,
∴AC⊥BD;
∵A(m, ),B(2m, ),
∴P(m, ),
∴PD=PB,
又AP=PC,
∴四边形ABCD是菱形;
(3)∵△ABP的面积为 BP AP=3,
∴BP AP=6,
∵P是AC的中点,
∴A点的纵坐标是B点纵坐标的2倍,
又∵点A. B都在双曲线y= (x>0)上,
∴B点的横坐标是A点横坐标的2倍,
∴OC=DP=BP,
∴k=OC AC=BP 2AP=12.
∴该双曲线的解析式是:y= .
23.(1)药物燃烧时,设y=kx,
将(4,8)代入,得:8=4k,
解得k=2,
则y=2x;
(2)药物燃尽后,设y=,
将(4,8)代入,得:8=,
解得:m=32,
则y=;
(3)在y=2x中,当y=2时,2x=2,解得x=1;
在y=中,当y=2时,=2,解得x=16;
则此次消毒有效时间为16﹣1=15分钟.
一、单选题(45分)
1.某气球充满一定质量的气体后,当温度不变时,气球内的气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示,当气球内的气压大于140kPa时,气球将爆炸,为了安全起见,气体体积应( )
A.不大于m3 B.不小于m3 C.不大于m3 D.不小于m3
2.点A(x1,y1),B(x2,y2)都在反比例函数的图象上,若x1<x2<0,则( )
A.y2>y1>0 B.y1>y2>0 C.y2<y1<0 D.y1<y2<0
3.某厂现有300吨煤,这些煤能烧的天数y与平均每天烧的吨数x之间的函数关系是( )
A.(x>0) B.(x≥0)
C.y=300x(x≥0) D.y=300x(x>0)
4.面积是160平方米的长方形,它的长y米,宽x米之间的关系表达式是( )
A.y=160x B.y= C.y=160+x D.y=160﹣x
5.某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种蔬菜.上图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图像,其中BC段是双曲线(k≠0)的一部分,则当x = 16时,大棚内的温度约为( )
A.18℃ B.15.5℃ C.13.5℃ D.12℃
6.已知力F对一个物体作的功是25焦,则力F与此物体在力在方向上移动的距离S之间的函数关系式的图象大致是( )
A.B.C.D.
7.甲、乙两地相距250千米,如果把汽车从甲地到乙地所用的时间y(小时),表示为汽车的平均速度为x(千米/小时)的函数,则此函数的图象大致是( ).
A. B. C.D.
8.已知一块蓄电池的电压为定值,以此蓄电池为电源时,电流I(A)与电阻R(Ω)之间的函数关系如图,则电流I关于电阻R的函数解析式为( )
A.I= B.I= C.I= D.I=-
9.如图,要围一个面积为20的矩形,若矩形的两邻边分别为、,则与的函数图象大致是( ).
A. B. C.D.
10.一台印刷机每年可印刷的书本数量y(万册)与它的使用时间x(年)成反比例关系,当x=2时,y=20.则y与x的函数图象大致是( )
A. B.
C. D.
11.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V (m3)的反比例函数,其图像如图所示.当气球内的气压大于140kPa时,气球将爆炸.为了安全起见,气体体积应( )
A.不大于 B.不小于 C.不大于 D.不小于
12.随着私家车的增加,交通也越来越拥挤,通常情况下,某段公路上车辆的行驶速度(千米/时)与路上每百米拥有车的数量x(辆)的关系如图所示,当x≥8时,y与x成反比例函数关系,当车速度低于20千米/时,交通就会拥堵,为避免出现交通拥堵,公路上每百米拥有车的数量x应该满足的范围是( )
A.x<32 B.x≤32 C.x>32 D.x≥32
13.某气球内充满了一定质量的气体,在温度不变的条件下,气球内气体的压强p(Pa)是气球体积V(m3)的反比例函数,且当V=1.5m3时,p=16000Pa,当气球内的气压大于40000Pa时,气球将爆炸,为确保气球不爆炸,气球的体积应( )
A.不小于0.5m3 B.不大于0.5m3 C.不小于0.6m3 D.不大于0.6m3
14.矩形面积为4,它的一边长y与邻边长x的函数关系用图象表示大致是( )
A.B.C.D.
15.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.则用电阻R表示电流I的函数表达式为( )
A. B. C. D.
二、填空题(15分)
16.一个水池装水12m3,如果从水管中每小时流出m3的水,经过h可以把水放完,那么 与的函数关系式是______,自变量的取值范围是______.
17.利用数学公式可建立反比例函数关系式,圆柱体的容积=_______×___.
18.一定质量的氧气,它的密度与它的体积V成反比例关系.当V=10m3时,=1.4kg/m3.则当=0.28kg/m3时,V=___.
19.学校内要设计一个面积是㎡长方形的运动场,则运动场的长与宽之间的函数关系式为________,当________时运动场是正方形.
20.一批零件600个,一个工人每小时做15个,用关系式表示人数x与完成任务所需的时间y之间的函数关系式为___________.
三、解答题(60分)
21.用洗衣粉洗衣物时,漂洗的次数与衣物中洗衣粉的残留量近似地满足反比例函数关系.某天,小金、小东放学回家后各自洗一件完全相同的衣服,漂洗时,小金每次用水约6升,小东每次用水约5升,他们都用了5克洗衣粉,第一次漂洗后,小金的衣服残留的洗衣粉还有1.5克,小东的衣服残留的洗衣粉还有2克.
(1)分别求出小金、小东衣服漂洗后洗衣粉残留量关于次数的函数解析式.
(2)已知洗衣粉的残留量降至0.35克时,便视为衣服漂洗干净,若以把衣服洗干净为前提,节约用水为目标,判断小金和小东两种漂洗方法用水量的大小,并说明理由.
22.如图,已知点A.B在双曲线y= (x>0)上,AC⊥x轴于C,BD⊥y轴于点D,AC与BD交于点P,P是AC的中点.
(1)设A的横坐标为m,试用m、k表示B的坐标.
(2)试判断四边形ABCD的形状,并说明理由.
(3)若△ABP的面积为3,求该双曲线的解析式.
23.为了预防“流感”,某学校对教室采用药熏法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(毫克/立方米)与药物点燃后的时间x(分钟)成正比例,药物燃尽后,y与x成反比例(如图所示).已知药物点燃后4分钟燃尽,此时室内每立方米空气中含药量为8毫克.
(1)求药物燃烧时,y与x之间函数的表达式;
(2)求药物燃尽后,y与x之间函数的表达式;
(3)研究表明,当空气中每立方米的含药量不低于2毫克时,才能有效杀灭空气中的病菌,那么此次消毒有效时间有多长?
参考答案
1--10BCABC BDCCC 11--15BBCAD
16. >0
17. 底面积 高
18.
19.
20.y=
21.(1)设小金衣服中洗衣粉的残留量与漂洗次数的函数关系式为:
则当
所以小金衣服中洗衣粉的残留量与漂洗次数的函数关系式为:
设小东衣服中洗衣粉的残留量与漂洗次数的函数关系式分别为:
则当
所以小东衣服中洗衣粉的残留量与漂洗次数的函数关系式分别为:
(2)把代入
可得:
可得洗衣的次数为5次,
所以小金用水升,
把代入
可得:
可得洗衣的次数为6次,
所以小东用水升,
所以小金的用水量与小东的用水量一样多.
22.(1)∵A的横坐标为m,AC⊥x轴于C,P是AC的中点,
∴点B的横坐标是2m.
又∵点B在双曲线y= (x>0)上,
∴B(2m,).
(2)连接AD、CD、BC;
∵AC⊥x轴于C,BD⊥y轴于点D,
∴AC⊥BD;
∵A(m, ),B(2m, ),
∴P(m, ),
∴PD=PB,
又AP=PC,
∴四边形ABCD是菱形;
(3)∵△ABP的面积为 BP AP=3,
∴BP AP=6,
∵P是AC的中点,
∴A点的纵坐标是B点纵坐标的2倍,
又∵点A. B都在双曲线y= (x>0)上,
∴B点的横坐标是A点横坐标的2倍,
∴OC=DP=BP,
∴k=OC AC=BP 2AP=12.
∴该双曲线的解析式是:y= .
23.(1)药物燃烧时,设y=kx,
将(4,8)代入,得:8=4k,
解得k=2,
则y=2x;
(2)药物燃尽后,设y=,
将(4,8)代入,得:8=,
解得:m=32,
则y=;
(3)在y=2x中,当y=2时,2x=2,解得x=1;
在y=中,当y=2时,=2,解得x=16;
则此次消毒有效时间为16﹣1=15分钟.
