人教版数学七上4.2.2 线段长短的比较与运算教案(无答案)
文档属性
| 名称 | 人教版数学七上4.2.2 线段长短的比较与运算教案(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 236.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-29 08:21:27 | ||
图片预览


文档简介
4.2.2 线段长短的比较与运算
课题 4.2.2 线段长短的比较与运算
学习目标 1.会画一条线段等于已知线段,会比较两条线段的大小. 2.通过实例体会两点之间线段最短的性质,并能初步应用. 3.了解两点间的距离、线段的中点以及线段的三等分点的意义.
学习重点 线段的性质及线段大小比较
学习难点 线段上中点、三等分点、四等分点的表示方法及运用;两点间的距离
学习流程: 教学互动
一、情境导入 做手工时,在没有刻度尺的条件下,若想从较长的木棍上截下一段,使截下的木棒等于另一根短木棒的长,我们常采用以上办法. 你们平时是如何比较两个同学的身高的?你能从比身高的方法中得到启示来比较两条线段的长短吗?
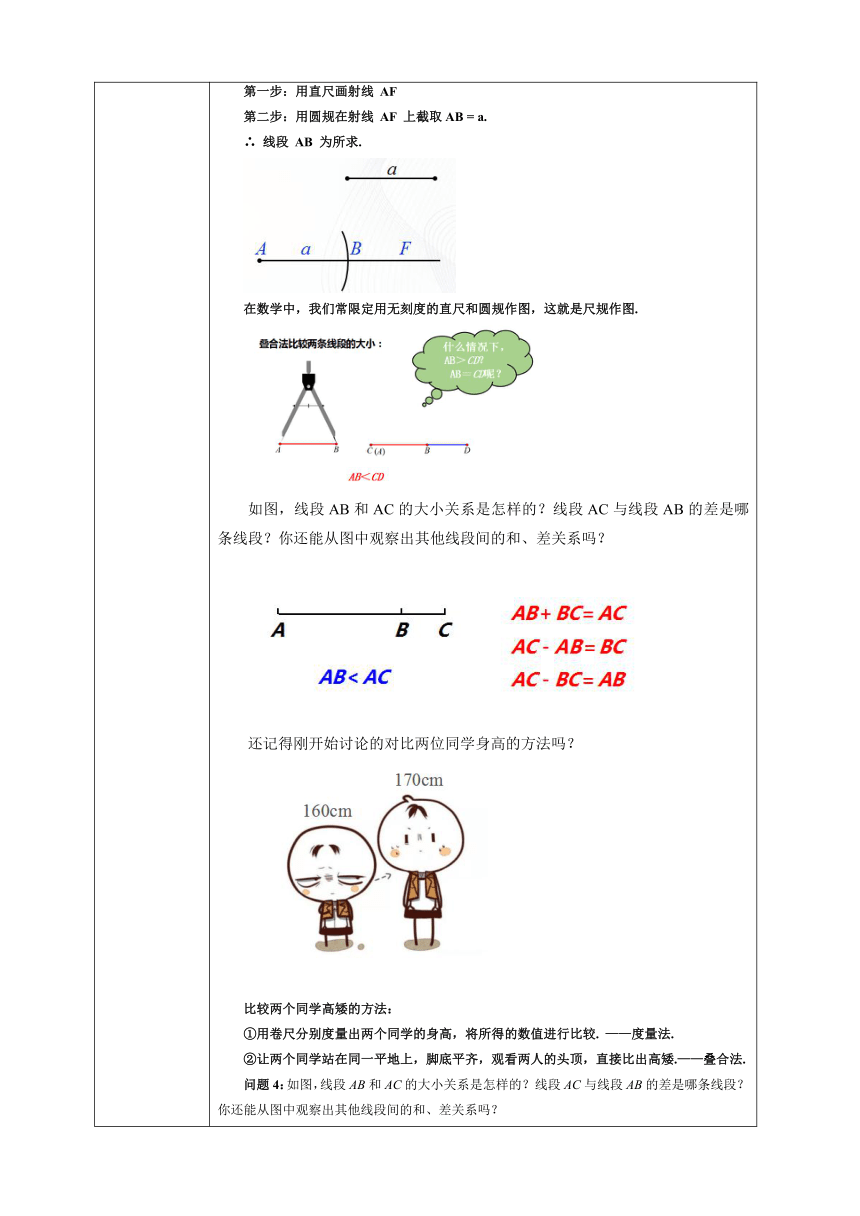
二、新知探究 观察这三组图形,你能比较出每组图形中线段 a 和 b 的长短吗? 三组图形中,线段a与b的长度均相等 很多时候,眼见未必为实. 准确比较线段的长短还需要更加严谨的办法. 作一条线段等于已知线段 已知:线段 a,作一条线段 AB,使 AB=a. 第一步:用直尺画射线 AF 第二步:用圆规在射线 AF 上截取AB = a. ∴ 线段 AB 为所求. 在数学中,我们常限定用无刻度的直尺和圆规作图,这就是尺规作图. 如图,线段AB和AC的大小关系是怎样的?线段AC与线段AB的差是哪条线段?你还能从图中观察出其他线段间的和、差关系吗? 还记得刚开始讨论的对比两位同学身高的方法吗? 比较两个同学高矮的方法: ①用卷尺分别度量出两个同学的身高,将所得的数值进行比较. ——度量法. ②让两个同学站在同一平地上,脚底平齐,观看两人的头顶,直接比出高矮.——叠合法. 问题4:如图,线段AB和AC的大小关系是怎样的?线段AC与线段AB的差是哪条线段?你还能从图中观察出其他线段间的和、差关系吗? 答案:AB<AC AB+BC=AC AC-AB=BC AC-BC=AB 问题5:如图,已知线段a和线段b,怎样通过作图得到a与b的和、a与b的差呢? 答案: AC=a+b CB=a-b 问题6:如图,已知线段a,求作线段AB=2a. 答案: AB=2a 强调:点M把线段AB分成相等的两条线段AM与BM,点M叫做线段AB的中点. 符号语言:∵M是AB的中点 ∴AM=BM=AB 想一想:什么是三等分点?四等分点呢? 问题7:如图,从A地到B地有四条道路,除它们外能否再修一条从A地到B地的最短道路?如果能,请联系你以前所学的知识,在图上画出最短路线. 强调1:两点的所有连线中,线段最短.简单地说:两点之间,线段最短. 强调2:连接两点间的线段的长度,叫做这两点的距离.
过关练习 1.如图,下列关系式中与图不符的是( ) A.AD-CD=ACB. AB+BC=AC C.BD-BC=AB+BC D. AD-BD=AC-BC 答案:C 2.如图,点P是线段AB的中点,点Q是线段AP的中点,如果PQ=2 cm,则BQ的长为( ) A.2 cm B.4 cm C.6 cm D.8 cm 答案:C 3.如图,由A到B有①②③三条路线,则最短的路线是_______(填序号),理由是_____________. 答案:②,两点之间,线段最短 4.下列说法正确的是( ) A.连接两点的线段叫做两点间的距离 B.两点间连线的长度叫做两点间的距离 C.连接两点的直线的长度叫做两点间的距离 D.连接两点的线段的长度叫做两点间的距离 答案:D 5.如图,已知点C在线段AB上,线段AC=12,BC=8,点M,N分别是AC,BC的中点,求线段MN的长度; 根据上面的计算过程与结果,设AC+BC=a,其他条件不变,你能猜出MN的长度吗?用简练的语言表述你发现的规律. 解:(1)因为MC=AC,NC=BC, 所以MN=AC+BC=×12+×8=10 (2)因为MC=AC,NC=BC, 所以MN=AC+BC=×12+×8=10
课堂小结 要点1 线段长短的比较 比较两条线段的长短.我们可以用刻度尺分别测量出它们的来比较,即度量法;或用圆规把其中一条线段移到另一条线段上作比较,即叠合法. 要点2 线段的中点 把一条线段分成的两条线段的点,叫做线段的中点. 要点3 线段的性质 1. 线段的基本事实:两点之间,最短. 2. 两点的距离是指连接两点间的线段的 答案: 要点1 长度 要点2 相等 要点3 1. 线段 2. 长度
三、体验收获 今天我们学习了哪些知识? 1.如何画一条线段等于已知线段? 2.怎样比较两条线段的大小? 3.什么是线段的中点?(三等分点等) 4.关于线段的基本事实是什么? 5.说一说两点的距离的定义?
四、达标测评 1. 已知线段AB和线段CD,使端点A与C重合,若点D在线段AB的延长线上,则有( ) A. AB>CD B. AB=CD C. AB五、布置作业 课后练习册
课题 4.2.2 线段长短的比较与运算
学习目标 1.会画一条线段等于已知线段,会比较两条线段的大小. 2.通过实例体会两点之间线段最短的性质,并能初步应用. 3.了解两点间的距离、线段的中点以及线段的三等分点的意义.
学习重点 线段的性质及线段大小比较
学习难点 线段上中点、三等分点、四等分点的表示方法及运用;两点间的距离
学习流程: 教学互动
一、情境导入 做手工时,在没有刻度尺的条件下,若想从较长的木棍上截下一段,使截下的木棒等于另一根短木棒的长,我们常采用以上办法. 你们平时是如何比较两个同学的身高的?你能从比身高的方法中得到启示来比较两条线段的长短吗?
二、新知探究 观察这三组图形,你能比较出每组图形中线段 a 和 b 的长短吗? 三组图形中,线段a与b的长度均相等 很多时候,眼见未必为实. 准确比较线段的长短还需要更加严谨的办法. 作一条线段等于已知线段 已知:线段 a,作一条线段 AB,使 AB=a. 第一步:用直尺画射线 AF 第二步:用圆规在射线 AF 上截取AB = a. ∴ 线段 AB 为所求. 在数学中,我们常限定用无刻度的直尺和圆规作图,这就是尺规作图. 如图,线段AB和AC的大小关系是怎样的?线段AC与线段AB的差是哪条线段?你还能从图中观察出其他线段间的和、差关系吗? 还记得刚开始讨论的对比两位同学身高的方法吗? 比较两个同学高矮的方法: ①用卷尺分别度量出两个同学的身高,将所得的数值进行比较. ——度量法. ②让两个同学站在同一平地上,脚底平齐,观看两人的头顶,直接比出高矮.——叠合法. 问题4:如图,线段AB和AC的大小关系是怎样的?线段AC与线段AB的差是哪条线段?你还能从图中观察出其他线段间的和、差关系吗? 答案:AB<AC AB+BC=AC AC-AB=BC AC-BC=AB 问题5:如图,已知线段a和线段b,怎样通过作图得到a与b的和、a与b的差呢? 答案: AC=a+b CB=a-b 问题6:如图,已知线段a,求作线段AB=2a. 答案: AB=2a 强调:点M把线段AB分成相等的两条线段AM与BM,点M叫做线段AB的中点. 符号语言:∵M是AB的中点 ∴AM=BM=AB 想一想:什么是三等分点?四等分点呢? 问题7:如图,从A地到B地有四条道路,除它们外能否再修一条从A地到B地的最短道路?如果能,请联系你以前所学的知识,在图上画出最短路线. 强调1:两点的所有连线中,线段最短.简单地说:两点之间,线段最短. 强调2:连接两点间的线段的长度,叫做这两点的距离.
过关练习 1.如图,下列关系式中与图不符的是( ) A.AD-CD=ACB. AB+BC=AC C.BD-BC=AB+BC D. AD-BD=AC-BC 答案:C 2.如图,点P是线段AB的中点,点Q是线段AP的中点,如果PQ=2 cm,则BQ的长为( ) A.2 cm B.4 cm C.6 cm D.8 cm 答案:C 3.如图,由A到B有①②③三条路线,则最短的路线是_______(填序号),理由是_____________. 答案:②,两点之间,线段最短 4.下列说法正确的是( ) A.连接两点的线段叫做两点间的距离 B.两点间连线的长度叫做两点间的距离 C.连接两点的直线的长度叫做两点间的距离 D.连接两点的线段的长度叫做两点间的距离 答案:D 5.如图,已知点C在线段AB上,线段AC=12,BC=8,点M,N分别是AC,BC的中点,求线段MN的长度; 根据上面的计算过程与结果,设AC+BC=a,其他条件不变,你能猜出MN的长度吗?用简练的语言表述你发现的规律. 解:(1)因为MC=AC,NC=BC, 所以MN=AC+BC=×12+×8=10 (2)因为MC=AC,NC=BC, 所以MN=AC+BC=×12+×8=10
课堂小结 要点1 线段长短的比较 比较两条线段的长短.我们可以用刻度尺分别测量出它们的来比较,即度量法;或用圆规把其中一条线段移到另一条线段上作比较,即叠合法. 要点2 线段的中点 把一条线段分成的两条线段的点,叫做线段的中点. 要点3 线段的性质 1. 线段的基本事实:两点之间,最短. 2. 两点的距离是指连接两点间的线段的 答案: 要点1 长度 要点2 相等 要点3 1. 线段 2. 长度
三、体验收获 今天我们学习了哪些知识? 1.如何画一条线段等于已知线段? 2.怎样比较两条线段的大小? 3.什么是线段的中点?(三等分点等) 4.关于线段的基本事实是什么? 5.说一说两点的距离的定义?
四、达标测评 1. 已知线段AB和线段CD,使端点A与C重合,若点D在线段AB的延长线上,则有( ) A. AB>CD B. AB=CD C. AB
