人教版数学七上第四章 几何图形初步4.3.3余角和补角教案(无答案)
文档属性
| 名称 | 人教版数学七上第四章 几何图形初步4.3.3余角和补角教案(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 823.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-29 08:24:27 | ||
图片预览

文档简介
4.3.3 余角和补角
课题 4.3.3 余角和补角
学习目标 1.在具体情境中了解余角、补角的概念; 2.了解等角的余角与补角的性质,能运用这个性质解决简单的实际问题; 3.学习进行简单的推理,学习有条理的表达。
学习重点 认识角的互余、互补关系及其性质,方位角的判别
学习难点 余角、补角的性质和方位角的应用
学习流程: 教学互动
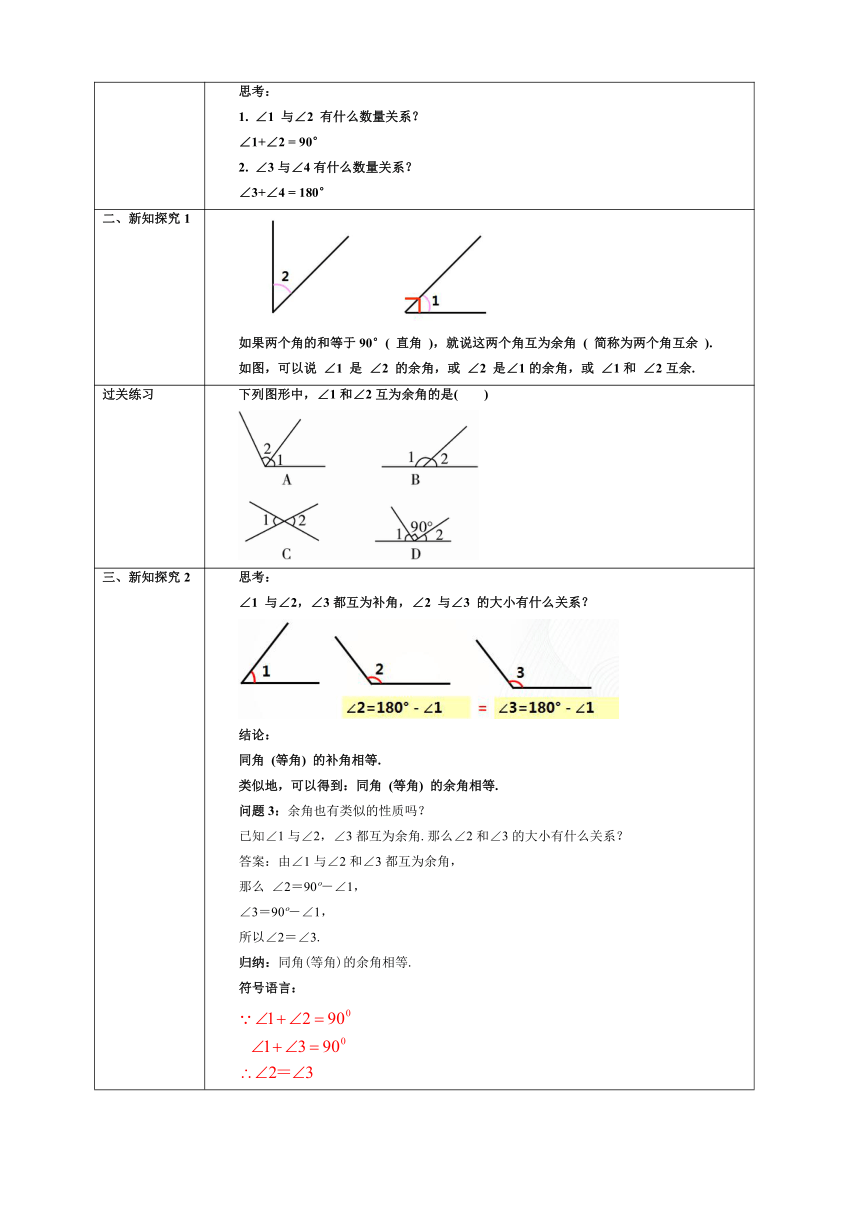
一、新知导入 观赏意大利名胜比萨斜塔 比莎斜塔的底部是石头堆砌而成的,量角器无法进入底部测量,如何得到比萨斜塔偏离竖直的角度? 将一张长方形纸片,沿一个角折叠后,折痕与长方形的边形成了4个角. 思考: 1. ∠1 与∠2 有什么数量关系? ∠1+∠2 = 90° 2. ∠3与∠4有什么数量关系? ∠3+∠4 = 180°
二、新知探究1 如果两个角的和等于90°( 直角 ),就说这两个角互为余角 ( 简称为两个角互余 ). 如图,可以说 ∠1 是 ∠2 的余角,或 ∠2 是∠1的余角,或 ∠1和 ∠2互余.
过关练习 下列图形中,∠1和∠2互为余角的是( )
三、新知探究2 思考: ∠1 与∠2,∠3都互为补角,∠2 与∠3 的大小有什么关系? 结论: 同角 (等角) 的补角相等. 类似地,可以得到:同角 (等角) 的余角相等. 问题3:余角也有类似的性质吗? 已知∠1与∠2,∠3都互为余角.那么∠2和∠3的大小有什么关系? 答案:由∠1与∠2和∠3都互为余角, 那么 ∠2=90 -∠1, ∠3=90 -∠1, 所以∠2=∠3. 归纳:同角(等角)的余角相等. 符号语言:
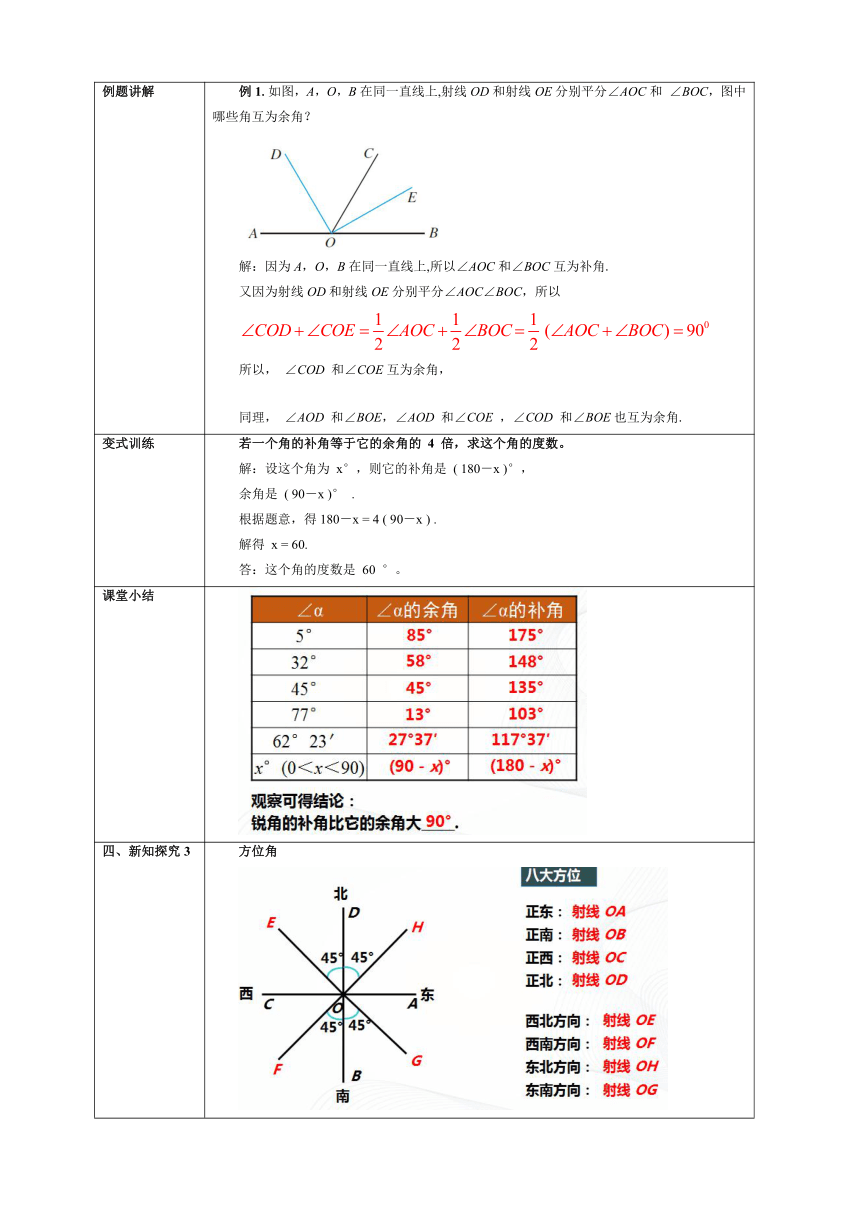
例题讲解 例1.如图,A,O,B在同一直线上,射线OD和射线OE分别平分∠AOC和 ∠BOC,图中哪些角互为余角? 解:因为A,O,B在同一直线上,所以∠AOC和∠BOC互为补角. 又因为射线OD和射线OE分别平分∠AOC∠BOC,所以 所以, ∠COD 和∠COE互为余角, 同理, ∠AOD 和∠BOE,∠AOD 和∠COE ,∠COD 和∠BOE也互为余角.
变式训练 若一个角的补角等于它的余角的 4 倍,求这个角的度数。 解:设这个角为 x°,则它的补角是 ( 180-x )°, 余角是 ( 90-x )° . 根据题意,得180-x = 4 ( 90-x ) . 解得 x = 60. 答:这个角的度数是 60 °。
课堂小结
四、新知探究3 方位角 如图,说出下列方位 例4.如图,货轮O在航行过程中,发现灯塔A在它南偏东60 的方向上,同时,在它北偏东40 、南偏西10 、西北(即北偏西45 )方向上又分别发现了客轮B,货轮C和海岛D.仿照表示灯塔方位的方法,画出表示客轮B、货轮C和海岛D方向的射线. 指出:有时以正北、正南方向为基准,描述物体运动的方向.表示方向的角(方位角)在航行、测绘等工作中经常用到. 答案: 变式训练 费俊龙、聂海胜乘坐“神舟”六号遨游太空时,我国当时派出远望一号~四号船队,跟踪检测. 其中远望一、二号停在太平洋洋面上,某一时刻,分别测得神舟六号在北偏东60°和北偏东30°的方向,你能在下图中画出当时神舟六号所处的位置吗?
过关练习 1.如果一个角的余角等于它本身,那么这个角等于_______;若一个角的补角等于它本身,则这个角等于_______. 答案:45°;90° 2.若∠1+∠2=90°,∠2+∠3=90°,那么∠1=∠3,根据是_________________;如果∠1+∠2=180°,∠3+∠4=180°,且∠1=∠3,那么∠2=∠4,根据是_______________. 答案:同角的余角相等;等角的补角相等 3.如图,下列说法正确的个数有() ①射线OA表示北偏东30°;②射线OB表示北偏西30°;③射线OD表示南偏西45°,也叫西南方向;④射线OC表示正南方向. A.1个 B.2个 C.3个 D.4个 答案:D 4.已知∠α与∠β互余,且∠α比∠β小25°,求2∠α-∠β的值. 解:设∠α的度数为x°,则∠β的度数为(x+25)°, 因为∠α与∠β互余, 所以x+x+25=90, 解得x=32.5, 即∠α=32.5°, 则∠β=57.5°, 所以2∠α-∠β=2×32.5°-×57.5°=53.5°
课堂小结 要点1 余角、补角的概念与性质 1. 一般地,如果两个角的和等于,就说这两个角互为余角,即其中一个角是另一个角的;类似地,如果两个角的和等于,就说这两个角互为补角,即其中一个角是另一个角的. 2. 同角(等角)的补角,同角(等角)的余角. 要点1 1. 90° 余角 180° 补角 2. 相等 相等 要点2 方位角 方位角就是表示的角,一般以、方向为基准,描述物体运动的方向.记录时,通常要先写偏或偏,再写东或西. 要点2 方向 正北 正南 北 南
四、体验收获 今天我们学习了哪些知识? 1.说一说什么是互余?什么是互补? 2.余角和补角有什么性质? 3.什么是方位角?
五、达标测评 1.已知∠A=65°,则∠A的补角等于( ) A.125° B.105° C.115° D.95° 答案:C 2.已知α=36°42′,则α的余角为( ) A.57°18′ B.52°18′ C.53°18′ D.36°43′ 答案:C 3.对于互补的下列说法中:①∠A+∠B+∠C=90°,则∠A,∠B,∠C互补;②若∠1是∠2的补角,则∠2是∠1的补角;③同一个锐角的补角一定比它的余角大90°;④互补的两个角中,一定是一个钝角与一个锐角.其中正确的有( ) A.1个 B.2个 C.3个 D.4个 答案:B 4.如图,下列说法正确的个数有( ) ①射线OA表示北偏东30°; ②射线OB表示北偏西30°; ③射线OD表示南偏西45°, 也叫西南方向; ④射线OC表示正南方向. A.1个 B.2个 C.3个 D.4个 答案:D 5. 如图,∠AOB=160°,∠AOD与∠DOC互余,∠BOD=90°,求∠COD的度数. 解:因为∠AOB=160°,∠BOD=90°, 所以∠AOD=70°. 因为∠AOD与∠DOC互余,所以∠AOD+∠DOC=90°. 所以∠COD=90°-∠AOD=90°-70°=20°. 6. 甲、乙两船同时从小岛A出发,甲的速度为30海里/时,向北偏东20°方向航行,乙沿南偏东70°的方向以40海里/时的速度航行,半小时后甲、乙分别到达B,C两处. (1)以1cm表示10海里,在图中画出B,C的位置; (2)求∠BAC的度数; (3)量出B,C的图上距离,并换算出实际距离. 解:(1)如图, (2)∠BAC=180°-20°-70°=90°. (3)用刻度尺量出B,C的图上距离约为2.5cm,所以实际距离约为25海里.
六、布置作业 教材练习题1—3题
课题 4.3.3 余角和补角
学习目标 1.在具体情境中了解余角、补角的概念; 2.了解等角的余角与补角的性质,能运用这个性质解决简单的实际问题; 3.学习进行简单的推理,学习有条理的表达。
学习重点 认识角的互余、互补关系及其性质,方位角的判别
学习难点 余角、补角的性质和方位角的应用
学习流程: 教学互动
一、新知导入 观赏意大利名胜比萨斜塔 比莎斜塔的底部是石头堆砌而成的,量角器无法进入底部测量,如何得到比萨斜塔偏离竖直的角度? 将一张长方形纸片,沿一个角折叠后,折痕与长方形的边形成了4个角. 思考: 1. ∠1 与∠2 有什么数量关系? ∠1+∠2 = 90° 2. ∠3与∠4有什么数量关系? ∠3+∠4 = 180°
二、新知探究1 如果两个角的和等于90°( 直角 ),就说这两个角互为余角 ( 简称为两个角互余 ). 如图,可以说 ∠1 是 ∠2 的余角,或 ∠2 是∠1的余角,或 ∠1和 ∠2互余.
过关练习 下列图形中,∠1和∠2互为余角的是( )
三、新知探究2 思考: ∠1 与∠2,∠3都互为补角,∠2 与∠3 的大小有什么关系? 结论: 同角 (等角) 的补角相等. 类似地,可以得到:同角 (等角) 的余角相等. 问题3:余角也有类似的性质吗? 已知∠1与∠2,∠3都互为余角.那么∠2和∠3的大小有什么关系? 答案:由∠1与∠2和∠3都互为余角, 那么 ∠2=90 -∠1, ∠3=90 -∠1, 所以∠2=∠3. 归纳:同角(等角)的余角相等. 符号语言:
例题讲解 例1.如图,A,O,B在同一直线上,射线OD和射线OE分别平分∠AOC和 ∠BOC,图中哪些角互为余角? 解:因为A,O,B在同一直线上,所以∠AOC和∠BOC互为补角. 又因为射线OD和射线OE分别平分∠AOC∠BOC,所以 所以, ∠COD 和∠COE互为余角, 同理, ∠AOD 和∠BOE,∠AOD 和∠COE ,∠COD 和∠BOE也互为余角.
变式训练 若一个角的补角等于它的余角的 4 倍,求这个角的度数。 解:设这个角为 x°,则它的补角是 ( 180-x )°, 余角是 ( 90-x )° . 根据题意,得180-x = 4 ( 90-x ) . 解得 x = 60. 答:这个角的度数是 60 °。
课堂小结
四、新知探究3 方位角 如图,说出下列方位 例4.如图,货轮O在航行过程中,发现灯塔A在它南偏东60 的方向上,同时,在它北偏东40 、南偏西10 、西北(即北偏西45 )方向上又分别发现了客轮B,货轮C和海岛D.仿照表示灯塔方位的方法,画出表示客轮B、货轮C和海岛D方向的射线. 指出:有时以正北、正南方向为基准,描述物体运动的方向.表示方向的角(方位角)在航行、测绘等工作中经常用到. 答案: 变式训练 费俊龙、聂海胜乘坐“神舟”六号遨游太空时,我国当时派出远望一号~四号船队,跟踪检测. 其中远望一、二号停在太平洋洋面上,某一时刻,分别测得神舟六号在北偏东60°和北偏东30°的方向,你能在下图中画出当时神舟六号所处的位置吗?
过关练习 1.如果一个角的余角等于它本身,那么这个角等于_______;若一个角的补角等于它本身,则这个角等于_______. 答案:45°;90° 2.若∠1+∠2=90°,∠2+∠3=90°,那么∠1=∠3,根据是_________________;如果∠1+∠2=180°,∠3+∠4=180°,且∠1=∠3,那么∠2=∠4,根据是_______________. 答案:同角的余角相等;等角的补角相等 3.如图,下列说法正确的个数有() ①射线OA表示北偏东30°;②射线OB表示北偏西30°;③射线OD表示南偏西45°,也叫西南方向;④射线OC表示正南方向. A.1个 B.2个 C.3个 D.4个 答案:D 4.已知∠α与∠β互余,且∠α比∠β小25°,求2∠α-∠β的值. 解:设∠α的度数为x°,则∠β的度数为(x+25)°, 因为∠α与∠β互余, 所以x+x+25=90, 解得x=32.5, 即∠α=32.5°, 则∠β=57.5°, 所以2∠α-∠β=2×32.5°-×57.5°=53.5°
课堂小结 要点1 余角、补角的概念与性质 1. 一般地,如果两个角的和等于,就说这两个角互为余角,即其中一个角是另一个角的;类似地,如果两个角的和等于,就说这两个角互为补角,即其中一个角是另一个角的. 2. 同角(等角)的补角,同角(等角)的余角. 要点1 1. 90° 余角 180° 补角 2. 相等 相等 要点2 方位角 方位角就是表示的角,一般以、方向为基准,描述物体运动的方向.记录时,通常要先写偏或偏,再写东或西. 要点2 方向 正北 正南 北 南
四、体验收获 今天我们学习了哪些知识? 1.说一说什么是互余?什么是互补? 2.余角和补角有什么性质? 3.什么是方位角?
五、达标测评 1.已知∠A=65°,则∠A的补角等于( ) A.125° B.105° C.115° D.95° 答案:C 2.已知α=36°42′,则α的余角为( ) A.57°18′ B.52°18′ C.53°18′ D.36°43′ 答案:C 3.对于互补的下列说法中:①∠A+∠B+∠C=90°,则∠A,∠B,∠C互补;②若∠1是∠2的补角,则∠2是∠1的补角;③同一个锐角的补角一定比它的余角大90°;④互补的两个角中,一定是一个钝角与一个锐角.其中正确的有( ) A.1个 B.2个 C.3个 D.4个 答案:B 4.如图,下列说法正确的个数有( ) ①射线OA表示北偏东30°; ②射线OB表示北偏西30°; ③射线OD表示南偏西45°, 也叫西南方向; ④射线OC表示正南方向. A.1个 B.2个 C.3个 D.4个 答案:D 5. 如图,∠AOB=160°,∠AOD与∠DOC互余,∠BOD=90°,求∠COD的度数. 解:因为∠AOB=160°,∠BOD=90°, 所以∠AOD=70°. 因为∠AOD与∠DOC互余,所以∠AOD+∠DOC=90°. 所以∠COD=90°-∠AOD=90°-70°=20°. 6. 甲、乙两船同时从小岛A出发,甲的速度为30海里/时,向北偏东20°方向航行,乙沿南偏东70°的方向以40海里/时的速度航行,半小时后甲、乙分别到达B,C两处. (1)以1cm表示10海里,在图中画出B,C的位置; (2)求∠BAC的度数; (3)量出B,C的图上距离,并换算出实际距离. 解:(1)如图, (2)∠BAC=180°-20°-70°=90°. (3)用刻度尺量出B,C的图上距离约为2.5cm,所以实际距离约为25海里.
六、布置作业 教材练习题1—3题
