人教版数学七上4.1.2 点、线、面、体教案
文档属性
| 名称 | 人教版数学七上4.1.2 点、线、面、体教案 |
|
|
| 格式 | zip | ||
| 文件大小 | 539.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-29 08:26:20 | ||
图片预览

文档简介
4.1.2 点、线、面、体
课题 4.1.2 点、线、面、体
学习目标 1.从不同方向观察一个物体,体会其观察结果的不一样性. 2.能画出从不同方向看一些基本几何体或其简单组合得到的平面图形. 3.初步建立空间观念.
学习重点 认识点、线、面、体的几何特征,感受它们之间的关系
学习难点 从实物或模型中抽象出概念,并举出确切的实例描述概念
学习流程: 教学互动
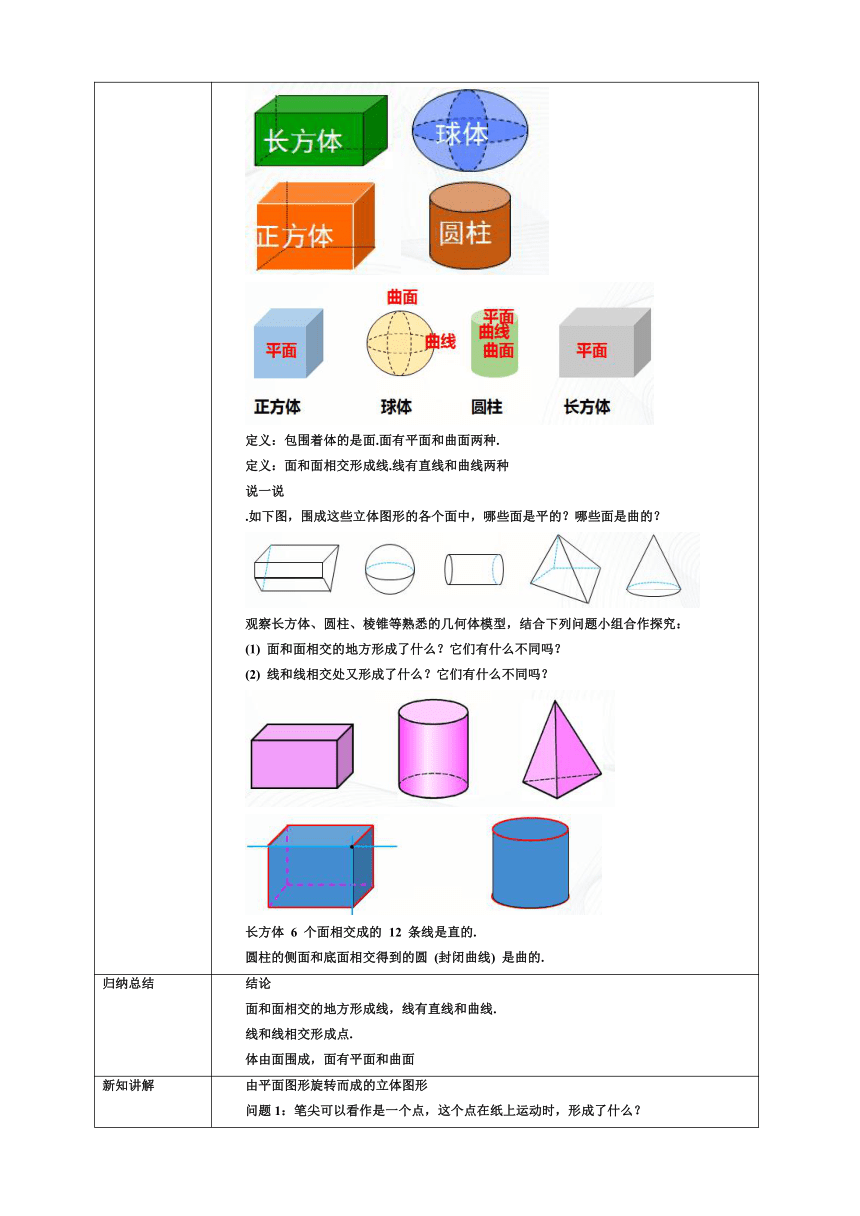
一、情境导入 图中有哪些你熟悉的立体图形?
二、新知探究 定义:以上立体图形都是几何体,简称体.包围着体的是面 定义:包围着体的是面.面有平面和曲面两种. 定义:面和面相交形成线.线有直线和曲线两种 说一说 .如下图,围成这些立体图形的各个面中,哪些面是平的?哪些面是曲的? 观察长方体、圆柱、棱锥等熟悉的几何体模型,结合下列问题小组合作探究: (1) 面和面相交的地方形成了什么?它们有什么不同吗? (2) 线和线相交处又形成了什么?它们有什么不同吗? 长方体 6 个面相交成的 12 条线是直的. 圆柱的侧面和底面相交得到的圆 (封闭曲线) 是曲的.
归纳总结 结论 面和面相交的地方形成线,线有直线和曲线. 线和线相交形成点. 体由面围成,面有平面和曲面
新知讲解 由平面图形旋转而成的立体图形 问题1:笔尖可以看作是一个点,这个点在纸上运动时,形成了什么? 这可以说成:点动成线. 问题2:雨刷器在挡风玻璃上的运动形成了一个扇形的痕迹,这一现象又能说明什么? 这可以说成:线动成面. 思考 一个长方形物体绕着它的一边旋转,形成一个圆柱体,这一现象又能说明什么? 这可以说成:面动成体
巩固提高 观察下列多面体,并把下表补充完整. 名称三棱柱四棱柱五棱柱六棱柱图形顶点数a61012棱数b912面数c5
观察上表中的结果,你能发现a+c与b之间有什么关系吗?请写出关系式. 解:每列从上到下依次为:8,6;15,7;18,8 关系式:a+c=b+2
课堂小结 1.几何图形都是由点、线、面、体组成的,点是构成图形的基本元素. 2. 线和线相交的地方是点;线有 直线 和曲线两种;面有平面和曲面两种;体是几何体的简称. 3.几何体简称体,包围着体的是 面 ,面和面相交的地方形成 线 ,线和线相交的地方形成 点 点动成线,线动成面,面动成体.
四、体验收获 今天我们学习了哪些知识 说一说点、线、面、体及它们之间的关系
五、达标测评 1. 如图所示,关于图中的几何体,下列叙述不正确的是( ) A. 四个几何体中,平面数最多的是图④ B. 图②有四个面是平面 C. 图①由两个面围成,其中一个面是曲面 D. 图中只有一个顶点的几何体是图③ 答案:C 2. 下列选项中的拼图,不是由图中这副七巧板拼成的是( ) 答案:B 3.下列现象能说明“面动成体”的是( ) A.时钟的钟摆摆动留下的痕迹 B.旋转一扇门,门在空中运动的轨迹 C.扔出一块小石子,石子在天空中飞行的路线 D.一根舞动的荧光棒 答案:B 4. 请你从数学的角度描述下列现象. (1)国庆之夜,炸响的礼花在天空中(瞬间)留下美丽的弧线; (2)用一条拉直的细线切一块豆腐; (3)将2078张十六开的白纸摞成长方体. 解:(1)点动成线. (2)线动成面. (3)面动成体. 5. 如下图,上面的平面图形绕轴旋转一周,可以得到下面的立体图形,把有对应关系的平面图形与立体图形连接起来. 6. 如图是一个七棱柱,它的底面边长都是2cm,侧棱长是5cm,观察这个棱柱,请回答下列问题: (1)这个七棱柱共有多少个面?它们分别是什么形状?哪些面的形状、面积完全相同?侧面的面积是多少?由此你可以猜想得出n棱柱有多少个面? (2)这个七棱柱一共有多少条棱?它们的长度分别是多少?这个七棱柱一共有多少个顶点? 解:(1)这个七棱柱共有九个面,上、下两个底面是七边形,侧面是长方形,上、下两个底面的形状相同,面积相等,七个侧面的面积是2×5×7=70(cm2).n个棱柱有(n+2)个面. (2)这个七棱柱一共有21条棱,它们的侧棱长是5cm,其余棱长为2cm.这个七棱柱一共有14个顶点.
六、布置作业 教材练习题1—3题.
课题 4.1.2 点、线、面、体
学习目标 1.从不同方向观察一个物体,体会其观察结果的不一样性. 2.能画出从不同方向看一些基本几何体或其简单组合得到的平面图形. 3.初步建立空间观念.
学习重点 认识点、线、面、体的几何特征,感受它们之间的关系
学习难点 从实物或模型中抽象出概念,并举出确切的实例描述概念
学习流程: 教学互动
一、情境导入 图中有哪些你熟悉的立体图形?
二、新知探究 定义:以上立体图形都是几何体,简称体.包围着体的是面 定义:包围着体的是面.面有平面和曲面两种. 定义:面和面相交形成线.线有直线和曲线两种 说一说 .如下图,围成这些立体图形的各个面中,哪些面是平的?哪些面是曲的? 观察长方体、圆柱、棱锥等熟悉的几何体模型,结合下列问题小组合作探究: (1) 面和面相交的地方形成了什么?它们有什么不同吗? (2) 线和线相交处又形成了什么?它们有什么不同吗? 长方体 6 个面相交成的 12 条线是直的. 圆柱的侧面和底面相交得到的圆 (封闭曲线) 是曲的.
归纳总结 结论 面和面相交的地方形成线,线有直线和曲线. 线和线相交形成点. 体由面围成,面有平面和曲面
新知讲解 由平面图形旋转而成的立体图形 问题1:笔尖可以看作是一个点,这个点在纸上运动时,形成了什么? 这可以说成:点动成线. 问题2:雨刷器在挡风玻璃上的运动形成了一个扇形的痕迹,这一现象又能说明什么? 这可以说成:线动成面. 思考 一个长方形物体绕着它的一边旋转,形成一个圆柱体,这一现象又能说明什么? 这可以说成:面动成体
巩固提高 观察下列多面体,并把下表补充完整. 名称三棱柱四棱柱五棱柱六棱柱图形顶点数a61012棱数b912面数c5
观察上表中的结果,你能发现a+c与b之间有什么关系吗?请写出关系式. 解:每列从上到下依次为:8,6;15,7;18,8 关系式:a+c=b+2
课堂小结 1.几何图形都是由点、线、面、体组成的,点是构成图形的基本元素. 2. 线和线相交的地方是点;线有 直线 和曲线两种;面有平面和曲面两种;体是几何体的简称. 3.几何体简称体,包围着体的是 面 ,面和面相交的地方形成 线 ,线和线相交的地方形成 点 点动成线,线动成面,面动成体.
四、体验收获 今天我们学习了哪些知识 说一说点、线、面、体及它们之间的关系
五、达标测评 1. 如图所示,关于图中的几何体,下列叙述不正确的是( ) A. 四个几何体中,平面数最多的是图④ B. 图②有四个面是平面 C. 图①由两个面围成,其中一个面是曲面 D. 图中只有一个顶点的几何体是图③ 答案:C 2. 下列选项中的拼图,不是由图中这副七巧板拼成的是( ) 答案:B 3.下列现象能说明“面动成体”的是( ) A.时钟的钟摆摆动留下的痕迹 B.旋转一扇门,门在空中运动的轨迹 C.扔出一块小石子,石子在天空中飞行的路线 D.一根舞动的荧光棒 答案:B 4. 请你从数学的角度描述下列现象. (1)国庆之夜,炸响的礼花在天空中(瞬间)留下美丽的弧线; (2)用一条拉直的细线切一块豆腐; (3)将2078张十六开的白纸摞成长方体. 解:(1)点动成线. (2)线动成面. (3)面动成体. 5. 如下图,上面的平面图形绕轴旋转一周,可以得到下面的立体图形,把有对应关系的平面图形与立体图形连接起来. 6. 如图是一个七棱柱,它的底面边长都是2cm,侧棱长是5cm,观察这个棱柱,请回答下列问题: (1)这个七棱柱共有多少个面?它们分别是什么形状?哪些面的形状、面积完全相同?侧面的面积是多少?由此你可以猜想得出n棱柱有多少个面? (2)这个七棱柱一共有多少条棱?它们的长度分别是多少?这个七棱柱一共有多少个顶点? 解:(1)这个七棱柱共有九个面,上、下两个底面是七边形,侧面是长方形,上、下两个底面的形状相同,面积相等,七个侧面的面积是2×5×7=70(cm2).n个棱柱有(n+2)个面. (2)这个七棱柱一共有21条棱,它们的侧棱长是5cm,其余棱长为2cm.这个七棱柱一共有14个顶点.
六、布置作业 教材练习题1—3题.
