2021-2022学年人教版数学八年级上册 14.1.1同底数幂的乘法 课件(共24张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学八年级上册 14.1.1同底数幂的乘法 课件(共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 441.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-28 19:38:39 | ||
图片预览






文档简介
(共24张PPT)
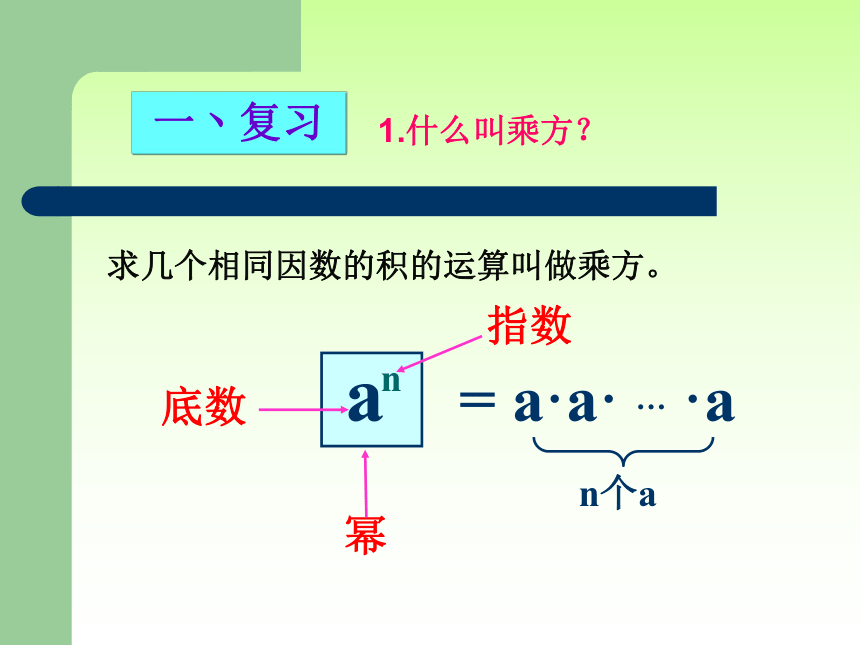
同底数幂的乘法
a
n
指数
幂
= a·a· … ·a
n个a
底数
1.什么叫乘方?
求几个相同因数的积的运算叫做乘方。
一丶复习
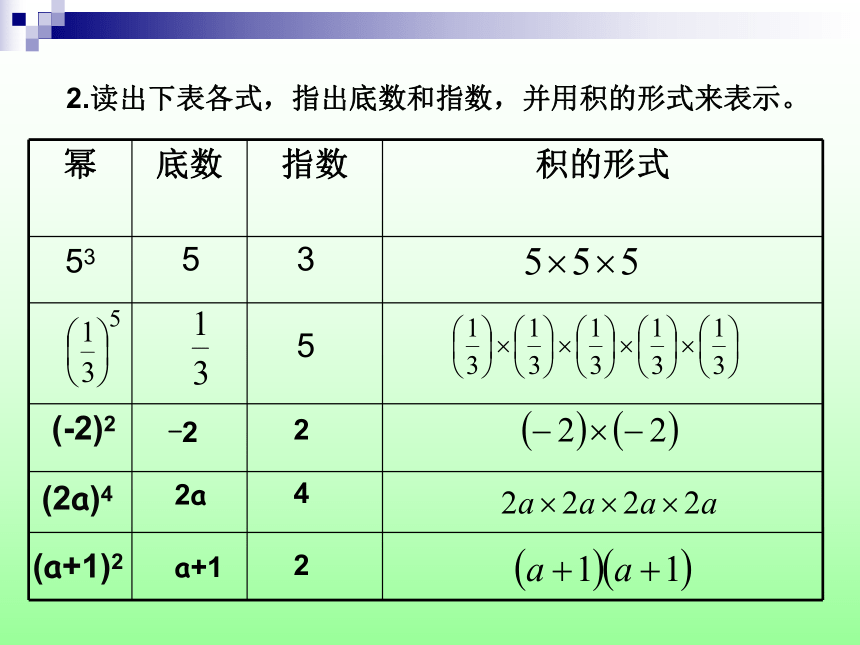
2.读出下表各式,指出底数和指数,并用积的形式来表示。
幂 底数 指数 积的形式
53
(-2)2
(2a)4
(a+1)2
5
3
5
-2
2
2a
4
a+1
2
创设情境引出课题
一种电子计算机 每秒可进行1014次运算,它工作103秒可进行多少次运算。
问题一:
分析:工作总量=工作时间x工作效率
1014 x 103
创设情境引出课题
问题二
光速:3 ×105km/s
时间:5 ×102s
路程 = 速度 x 时间
(3 ×10 5 ) × (5×10 2 )
=(3×5 ) × (10 5×10 2)
二丶尝试探讨,学习新知(一)
1丶观察下列四小题中的两个幂有什么共同点
2
5
-3
2丶计算下列各式,结果用幂的形式表示
二丶尝试探讨,学习新知(二)
2个2
3个2
(2+3)个2
解:原式=
(2x2)
x(2x2x2)
=(2x2x2x2x2)
=25
22 x 23
二丶尝试探讨,学习新知(三)
102x103
=(10x10)
=105
解:原式
2个10
3个10
=10x10x10x10x10
(2+3)个10
(2)
X(10x10x10)
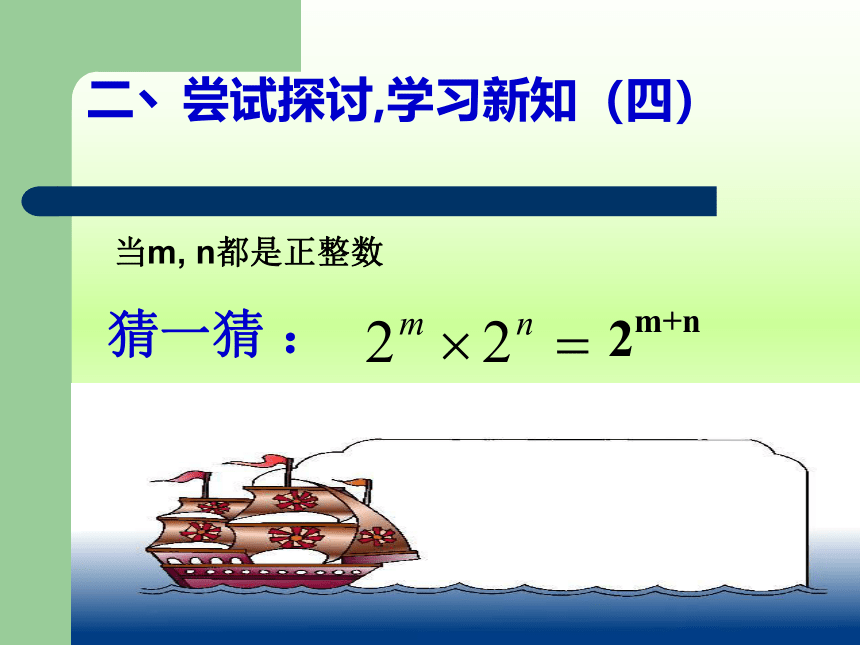
当m, n都是正整数
2m+n
二丶尝试探讨,学习新知(四)
猜一猜 :
m个2
n个2
(m+n)个2
=2m+n
哦!原理在这,我明白了。
解:原式
=(2x2x2x……x2)
x (2x2x2x……x2)
=(2x2x2x……x2)
说一说:
m n是正整数
让我来---看我的
am·an
解:am·an
=(a·a·a·……·a)
X(a·a·a·……·a)
m个a
n个a
=(a·a·a·……·a)
(m+n)个a
=am+n
想一想:
当m, n都是正整数
同底数的幂相乘,底数不变,指数相加。
底数不变
指数相加
同底数幂的乘法法则:
(m,n为正整数)
(m,n,p为正整数)
例1 计算下列各式,结果用幂的形式表示:
⑴x2 x5
三丶应用练习 促进深化
(3)2x24x23
三丶应用练习 促进深化
(6)xm x3m+1
计算:(抢答)
(1011 )
( a10 )
( x10 )
( b6 )
(2) a7 ·a3
(3) x5 ·x5
(4) b5 · b
(1) 105×106
Good!
计算下列各式,结果用幂的形式表示:
练一练
(3)x2 . X5 =
x7
(4)22 x 24m x 23n =
22+4m+3n
下面的计算对不 对?如果不对,应怎样改正?
⑴
⑶
⑵
辩一辩
① a · a2 = a2
② a+ a2 = a3
③ a3 · a3 = a9
④ a3+a3 = a6
判断下列计算是否正确,并简要说明理由:
再辩一辩
(×)
(×)
(×)
(×)
Are you clear
(1) x4 = x9
(2) (-y)4 =(-y)11
(3) a2m =a3m
(4) (x-y)2 =(x-y)5
x5
(-y)7
am
(x-y)3
填一填
3 、计算:
解:原式=a1+2+3+4+5+6+7+8+9+10
=a55
算一算
a1﹒a2﹒a3……a10
本节课你学到了什么?
我学到了什么
?
知识
方法
同底数幂相乘,
底数不变 指数相加
am · an = am+n (m、n正整数)
“特殊→一般→特殊”
例子 公式 应用
必做题:P96.练习1
P104.1 (1)、(2) 题
选做题:(x-y)2x(y-x)3
-22x (-2)3
作业布置
思考题
(1) x n · xn+1 ;
(2) (x+y)3 · (x+y)4
解:
x n · xn+1 =
解:
(x+y)3 · (x+y)4 =
am · an = am+n
xn+(n+1)
= x2n+1
公式中的a可代表一个数、字母、式子等.
(x+y)3+4 =(x+y)7
别忘了复习和预习新课哦
同底数幂的乘法
a
n
指数
幂
= a·a· … ·a
n个a
底数
1.什么叫乘方?
求几个相同因数的积的运算叫做乘方。
一丶复习
2.读出下表各式,指出底数和指数,并用积的形式来表示。
幂 底数 指数 积的形式
53
(-2)2
(2a)4
(a+1)2
5
3
5
-2
2
2a
4
a+1
2
创设情境引出课题
一种电子计算机 每秒可进行1014次运算,它工作103秒可进行多少次运算。
问题一:
分析:工作总量=工作时间x工作效率
1014 x 103
创设情境引出课题
问题二
光速:3 ×105km/s
时间:5 ×102s
路程 = 速度 x 时间
(3 ×10 5 ) × (5×10 2 )
=(3×5 ) × (10 5×10 2)
二丶尝试探讨,学习新知(一)
1丶观察下列四小题中的两个幂有什么共同点
2
5
-3
2丶计算下列各式,结果用幂的形式表示
二丶尝试探讨,学习新知(二)
2个2
3个2
(2+3)个2
解:原式=
(2x2)
x(2x2x2)
=(2x2x2x2x2)
=25
22 x 23
二丶尝试探讨,学习新知(三)
102x103
=(10x10)
=105
解:原式
2个10
3个10
=10x10x10x10x10
(2+3)个10
(2)
X(10x10x10)
当m, n都是正整数
2m+n
二丶尝试探讨,学习新知(四)
猜一猜 :
m个2
n个2
(m+n)个2
=2m+n
哦!原理在这,我明白了。
解:原式
=(2x2x2x……x2)
x (2x2x2x……x2)
=(2x2x2x……x2)
说一说:
m n是正整数
让我来---看我的
am·an
解:am·an
=(a·a·a·……·a)
X(a·a·a·……·a)
m个a
n个a
=(a·a·a·……·a)
(m+n)个a
=am+n
想一想:
当m, n都是正整数
同底数的幂相乘,底数不变,指数相加。
底数不变
指数相加
同底数幂的乘法法则:
(m,n为正整数)
(m,n,p为正整数)
例1 计算下列各式,结果用幂的形式表示:
⑴x2 x5
三丶应用练习 促进深化
(3)2x24x23
三丶应用练习 促进深化
(6)xm x3m+1
计算:(抢答)
(1011 )
( a10 )
( x10 )
( b6 )
(2) a7 ·a3
(3) x5 ·x5
(4) b5 · b
(1) 105×106
Good!
计算下列各式,结果用幂的形式表示:
练一练
(3)x2 . X5 =
x7
(4)22 x 24m x 23n =
22+4m+3n
下面的计算对不 对?如果不对,应怎样改正?
⑴
⑶
⑵
辩一辩
① a · a2 = a2
② a+ a2 = a3
③ a3 · a3 = a9
④ a3+a3 = a6
判断下列计算是否正确,并简要说明理由:
再辩一辩
(×)
(×)
(×)
(×)
Are you clear
(1) x4 = x9
(2) (-y)4 =(-y)11
(3) a2m =a3m
(4) (x-y)2 =(x-y)5
x5
(-y)7
am
(x-y)3
填一填
3 、计算:
解:原式=a1+2+3+4+5+6+7+8+9+10
=a55
算一算
a1﹒a2﹒a3……a10
本节课你学到了什么?
我学到了什么
?
知识
方法
同底数幂相乘,
底数不变 指数相加
am · an = am+n (m、n正整数)
“特殊→一般→特殊”
例子 公式 应用
必做题:P96.练习1
P104.1 (1)、(2) 题
选做题:(x-y)2x(y-x)3
-22x (-2)3
作业布置
思考题
(1) x n · xn+1 ;
(2) (x+y)3 · (x+y)4
解:
x n · xn+1 =
解:
(x+y)3 · (x+y)4 =
am · an = am+n
xn+(n+1)
= x2n+1
公式中的a可代表一个数、字母、式子等.
(x+y)3+4 =(x+y)7
别忘了复习和预习新课哦
