人教版2021—2022学年九年级数学上册22.3.3二次函数中动态几何存在性问题类题通法课件(共17张PPT)
文档属性
| 名称 | 人教版2021—2022学年九年级数学上册22.3.3二次函数中动态几何存在性问题类题通法课件(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 219.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-28 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
二次函数中动态几何的存在性问题
由动点的运动引起几何图形的改变
二次函数中动态几何的存在性问题
探究存在点满足特殊几何特征
由点的坐标可知线段长
如图,若点A(-1,-1),点B(3,-1),点C(-1,2),则
(1)AB=________,
(2)AC=________,
(3)BC=________.
x
C(-1,2)
O
y
A(-1,-1)
B(3,-1)
3-(-1)=4
2-(-1)=3
水平线段AB=|xA-xB|
铅垂线段AC=|yA-yC|
斜线段BC 2=(xB-xC)2+(yB-yC)2
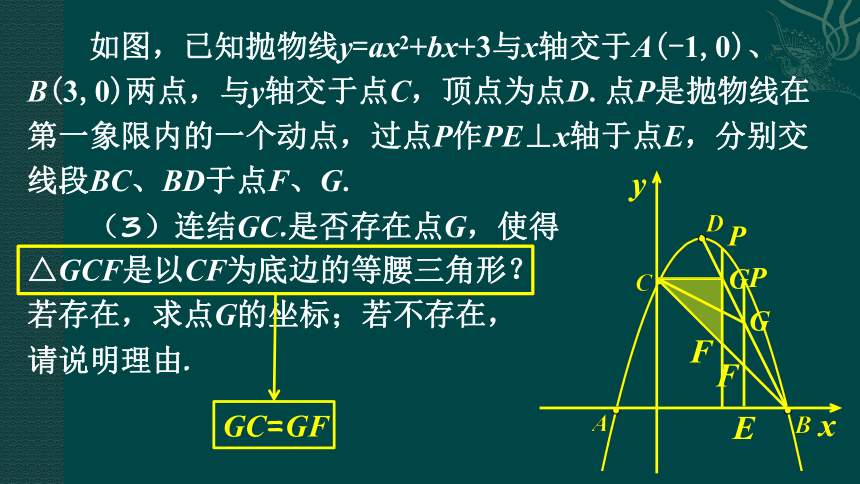
如图,已知抛物线y=ax2+bx+3与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C,顶点为点D.点P是抛物线在第一象限内的一个动点,过点P作PE⊥x轴于点E,分别交线段BC、BD于点F、G.
(1)求该抛物线所对应的函数关系式
及点D的坐标;
(2)是否存在点P,使得PG=GF?
若存在,求点P的坐标;若不存在,请
说明理由.
y
x
F
(1)抛物线y=-x2+2x+3,点D(1,4);
PG=GF
E
G
如图,已知抛物线y=ax2+bx+3与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C,顶点为点D.点P是抛物线在第一象限内的一个动点,过点P作PE⊥x轴于点E,分别交线段BC、BD于点F、G.
(3)连结GC.是否存在点G,使得
△GCF是以CF为底边的等腰三角形?
若存在,求点G的坐标;若不存在,
请说明理由.
y
x
F
G
GC=GF
E
F
G
P
P
如图,已知抛物线y=ax2+bx+3与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C,顶点为点D.点P是抛物线在第一象限内的一个动点,过点P作PE⊥x轴于点E,分别交线段BC、BD于点F、G.
(4)连结AG.是否存在点G,使得△ACG是以AG为斜边的直角三角形?若存在,求点G的坐标;若不存在,请说明理由.
(5)连结CD,PB.是否存在点P,使得△PEB与△BCD相似?若存在,求点P的坐标;若不存在,请说明理由.
(6)连结AC,PB.是否存在点P,使得∠PBE=∠CAO?
若存在,求点P的坐标;若不存在,请说明理由.
y
x
F
G
E
如图,已知抛物线y=ax2+bx+3与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C,顶点为点D.点P是抛物线在第一象限内的一个动点,过点P作PE⊥x轴于点E,分别交线段BC、BD于点F、G.
(4)连结AG.是否存在点G,使得△ACG
是以AG为斜边的直角三角形?若存在,求点G
的坐标;若不存在,请说明理由;
y
x
F
G
AC2+CG2=AG2
2
E
勾股定理
如图1,已知抛物线y=ax2+bx+3与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C,顶点为点D.点P是抛物线在第一象限内的一个动点,过点P作PE⊥x轴于点E,分别交线段BC、BD于点F、G.
(4)连结AG.是否存在点G,使得△ACG
是以AG为斜边的直角三角形?若存在,求点G
的坐标;若不存在,请说明理由;
y
x
M
G
D
B
A
C
N
△ANC∽△CMG
一线三垂直
1
E
如图1,已知抛物线y=ax2+bx+3与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C,顶点为点D.点P是抛物线在第一象限内的一个动点,过点P作PE⊥x轴于点E,分别交线段BC、BD于点F、G.
(5)连结CD,PB.是否存在点P,使得
△PEB与△BCD相似?若存在,求点P的坐标;
若不存在,请说明理由.
y
x
E
如图1,已知抛物线y=ax2+bx+3与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C,顶点为点D.点P是抛物线在第一象限内的一个动点,过点P作PE⊥x轴于点E,分别交线段BC、BD于点F、G.
(6)连结AC,PB.是否存在点P,使得
∠PBE=∠CAO?若存在,求点P的坐标;若
不存在,请说明理由.
y
x
E
tan∠PBE=tan∠CAO
△PEB∽△COA
y
x
E
y
x
E
y
x
M
G
D
B
A
C
N
y
x
F
G
(4)
(5)
(6)
(4)
E
E
二次函数中动态几何问题的解题思路
特殊几何特征
线段的数量关系
点的坐标
表示线段长
列方程
解方程
转
化
检验求解
1.求(设)点的坐标,
二次函数中动态几何问题的答题步骤
2.用代数式表示线段长,
3.列方程,
4.解方程,
5.检验求解。
万变不离其宗
以不变应万变
(海南中考.2020年)
抛物线y=x2+bx+c 经过点A (﹣3,0)和点B(2,0),与y轴交于点C.
(1)求该抛物线的函数表达式;
(2)点P为抛物线上的动点,且位于y轴的左侧.
①过点P作PD⊥x轴于点D,作PE⊥y轴
于点E,若PD=2PE时,求PE的长;
②在直线AC上是否存在点P,使得
∠ACP=∠OCB?若存在,请求出点P
的坐标;若不存在,请说明理由.
y
x
O
A
B
C
P
D
E
-6
-3
2
E
D
x
B
C
O
A
y
P
?
(2)点P为抛物线上的动点,且位于y轴的左侧.
①过点P作PD⊥x轴于点D,作PE⊥y轴于点E,若PD=2PE时,求PE的长;
设点P的坐标为( t,t2 + t -6 )(t<0)
则 D(t, 0),E(0,t2 + t -6);
EP =xE -xP= -t,PD =|t2 + t -6|;
t2 +t -6= -2t 或 t2 + t -6 = 2t
解这个方程,得
t 1 = … t2=…
-6
-3
2
x
B
C
O
A
y
P
M
②在直线AC上是否存在点P,使∠ACP=∠OCB?若存在,请求出点P的坐标;若不存在,请说明理由.
构造: △MAC∽△BOC
△MAC是以AC为边的Rt△
要使: ∠ACM=∠OCB
一线三垂直
二次函数中动态几何的存在性问题
由动点的运动引起几何图形的改变
二次函数中动态几何的存在性问题
探究存在点满足特殊几何特征
由点的坐标可知线段长
如图,若点A(-1,-1),点B(3,-1),点C(-1,2),则
(1)AB=________,
(2)AC=________,
(3)BC=________.
x
C(-1,2)
O
y
A(-1,-1)
B(3,-1)
3-(-1)=4
2-(-1)=3
水平线段AB=|xA-xB|
铅垂线段AC=|yA-yC|
斜线段BC 2=(xB-xC)2+(yB-yC)2
如图,已知抛物线y=ax2+bx+3与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C,顶点为点D.点P是抛物线在第一象限内的一个动点,过点P作PE⊥x轴于点E,分别交线段BC、BD于点F、G.
(1)求该抛物线所对应的函数关系式
及点D的坐标;
(2)是否存在点P,使得PG=GF?
若存在,求点P的坐标;若不存在,请
说明理由.
y
x
F
(1)抛物线y=-x2+2x+3,点D(1,4);
PG=GF
E
G
如图,已知抛物线y=ax2+bx+3与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C,顶点为点D.点P是抛物线在第一象限内的一个动点,过点P作PE⊥x轴于点E,分别交线段BC、BD于点F、G.
(3)连结GC.是否存在点G,使得
△GCF是以CF为底边的等腰三角形?
若存在,求点G的坐标;若不存在,
请说明理由.
y
x
F
G
GC=GF
E
F
G
P
P
如图,已知抛物线y=ax2+bx+3与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C,顶点为点D.点P是抛物线在第一象限内的一个动点,过点P作PE⊥x轴于点E,分别交线段BC、BD于点F、G.
(4)连结AG.是否存在点G,使得△ACG是以AG为斜边的直角三角形?若存在,求点G的坐标;若不存在,请说明理由.
(5)连结CD,PB.是否存在点P,使得△PEB与△BCD相似?若存在,求点P的坐标;若不存在,请说明理由.
(6)连结AC,PB.是否存在点P,使得∠PBE=∠CAO?
若存在,求点P的坐标;若不存在,请说明理由.
y
x
F
G
E
如图,已知抛物线y=ax2+bx+3与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C,顶点为点D.点P是抛物线在第一象限内的一个动点,过点P作PE⊥x轴于点E,分别交线段BC、BD于点F、G.
(4)连结AG.是否存在点G,使得△ACG
是以AG为斜边的直角三角形?若存在,求点G
的坐标;若不存在,请说明理由;
y
x
F
G
AC2+CG2=AG2
2
E
勾股定理
如图1,已知抛物线y=ax2+bx+3与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C,顶点为点D.点P是抛物线在第一象限内的一个动点,过点P作PE⊥x轴于点E,分别交线段BC、BD于点F、G.
(4)连结AG.是否存在点G,使得△ACG
是以AG为斜边的直角三角形?若存在,求点G
的坐标;若不存在,请说明理由;
y
x
M
G
D
B
A
C
N
△ANC∽△CMG
一线三垂直
1
E
如图1,已知抛物线y=ax2+bx+3与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C,顶点为点D.点P是抛物线在第一象限内的一个动点,过点P作PE⊥x轴于点E,分别交线段BC、BD于点F、G.
(5)连结CD,PB.是否存在点P,使得
△PEB与△BCD相似?若存在,求点P的坐标;
若不存在,请说明理由.
y
x
E
如图1,已知抛物线y=ax2+bx+3与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C,顶点为点D.点P是抛物线在第一象限内的一个动点,过点P作PE⊥x轴于点E,分别交线段BC、BD于点F、G.
(6)连结AC,PB.是否存在点P,使得
∠PBE=∠CAO?若存在,求点P的坐标;若
不存在,请说明理由.
y
x
E
tan∠PBE=tan∠CAO
△PEB∽△COA
y
x
E
y
x
E
y
x
M
G
D
B
A
C
N
y
x
F
G
(4)
(5)
(6)
(4)
E
E
二次函数中动态几何问题的解题思路
特殊几何特征
线段的数量关系
点的坐标
表示线段长
列方程
解方程
转
化
检验求解
1.求(设)点的坐标,
二次函数中动态几何问题的答题步骤
2.用代数式表示线段长,
3.列方程,
4.解方程,
5.检验求解。
万变不离其宗
以不变应万变
(海南中考.2020年)
抛物线y=x2+bx+c 经过点A (﹣3,0)和点B(2,0),与y轴交于点C.
(1)求该抛物线的函数表达式;
(2)点P为抛物线上的动点,且位于y轴的左侧.
①过点P作PD⊥x轴于点D,作PE⊥y轴
于点E,若PD=2PE时,求PE的长;
②在直线AC上是否存在点P,使得
∠ACP=∠OCB?若存在,请求出点P
的坐标;若不存在,请说明理由.
y
x
O
A
B
C
P
D
E
-6
-3
2
E
D
x
B
C
O
A
y
P
?
(2)点P为抛物线上的动点,且位于y轴的左侧.
①过点P作PD⊥x轴于点D,作PE⊥y轴于点E,若PD=2PE时,求PE的长;
设点P的坐标为( t,t2 + t -6 )(t<0)
则 D(t, 0),E(0,t2 + t -6);
EP =xE -xP= -t,PD =|t2 + t -6|;
t2 +t -6= -2t 或 t2 + t -6 = 2t
解这个方程,得
t 1 = … t2=…
-6
-3
2
x
B
C
O
A
y
P
M
②在直线AC上是否存在点P,使∠ACP=∠OCB?若存在,请求出点P的坐标;若不存在,请说明理由.
构造: △MAC∽△BOC
△MAC是以AC为边的Rt△
要使: ∠ACM=∠OCB
一线三垂直
同课章节目录
