2021-2022学年九年级数学下册人教版26.2 实际问题与反比例函数提高卷(word版含答案)
文档属性
| 名称 | 2021-2022学年九年级数学下册人教版26.2 实际问题与反比例函数提高卷(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 507.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-29 08:52:32 | ||
图片预览




文档简介
26.2实际问题与反比例函数提高卷
一、单选题(45分)
1.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压是气体体积的反比例函数,其图象如图所示,当气球内的气压大于时气球将爆炸.为了安全起见,气体的体积应满足( )
A. B. C. D.
2.已知长方形的面积为40cm2,相邻两边长分别为xcm和ycm,则y与x之间的函数图象是( )
A. B.
C. D.
3.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压与气体体积之间的函数关系如图所示.当气球的体积是,气球内的气压是( ).
A.96 B.150 C.120 D.64
4.某种气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气球体积V的反比例函数,其图象如图所示,当气球内的气压大于160 kPa时,气球将爆炸,为了安全,气球的体积应该( )
A.不大于m3 B.小于m3 C.不小于m3 D.小于m3
5.如图所示,点B、D在双曲线上,点A在双曲线上,且AD//y轴,AB//x轴, 以AB、AD为邻边作平行四边形ABCD,则平行四边形ABCD的面积是( )
A.4 B.6 C.8 D.10
6.1888年,海因里希 鲁道夫 赫兹证实了电磁波的存在,这成了后来大部分无线科技的基础.电磁波波长λ(单位:米)、频率f(单位:赫兹)满足函数关系λf=3×108,下列说法正确的是( )
A.电磁波波长是频率的正比例函数
B.电磁波波长20000米时,对应的频率1500赫兹
C.电磁波波长小于30000米时,频率小于10000赫兹
D.电磁波波长大于50000米时,频率小于6000赫兹
7.近似眼镜的度数(度)与镜片焦距(米)之间具有如图所示的反比例函数关系,若要配制一副度数小于400度的近似眼镜,则镜片焦距的取值范围是( )
A.0米米 B.米
C.0米米 D.米
8.已知某品牌显示器的使用寿命为定值.这种显示器可工作的天数y与平均每天工作的小时数x是反比例函数关系,图象如图所示.如果这种显示器至少要用2000天,那么显示器平均每天工作的小时数x应控制在( )
A. B. C. D.
9.一辆汽车匀速通过某段公路,所需时间(h)与行驶速度(km/h)满足函数关系点,其图象为如图所示的一段双曲线,端点为和,若行驶速度不得超过60 km/h,则汽车通过该路段最少需要( )
A.分钟 B.40分钟 C.60分钟 D.分钟
10.为了响应“绿水青山就是金山银山”的号召,建设生态文明,某工厂自2019年1月开始限产进行治污改造,其月利润y(万元)与月份x之间的变化如图所示,治污完成前是反比例函数图象的一部分,治污完成后是一次函数图象的一部分,下列选项错误的是( )
A.4月份的利润为50万元
B.治污改造完成后每月利润比前一个月增加30万元
C.治污改造完成前后共有3个月的利润低于100万元
D.8月份该厂利润达到200万元
11.已知:点A是双曲线在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为一边作等边三角形ABC,点C在第四象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式是( )
A. B. C.D.
12.如图,点A是双曲线y=﹣在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=上运动,则k的值为( )
A.3 B.4 C.2.5 D.7
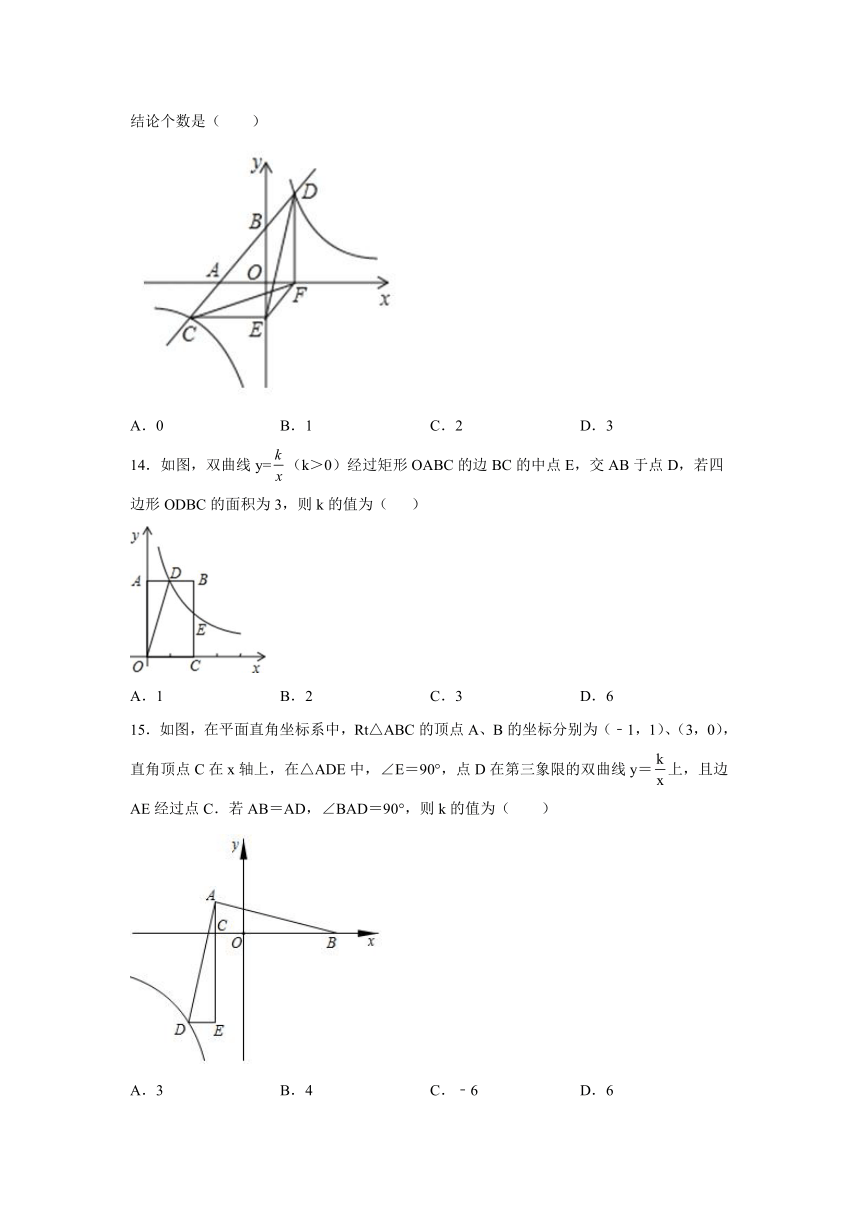
13.如图,一次函数y=ax+b与x轴、y轴交于A、B两点,与反比例函数y=相交于C、D两点,分别过C、D两点作y轴、x轴的垂线,垂足为E、F,连接CF、DE、EF. 有下列三个结论:①△CEF与△DEF的面积相等;②△DCE≌△CDF;③AC=BD.其中正确的结论个数是( )
A.0 B.1 C.2 D.3
14.如图,双曲线y=(k>0)经过矩形OABC的边BC的中点E,交AB于点D,若四边形ODBC的面积为3,则k的值为( )
A.1 B.2 C.3 D.6
15.如图,在平面直角坐标系中,Rt△ABC的顶点A、B的坐标分别为(﹣1,1)、(3,0),直角顶点C在x轴上,在△ADE中,∠E=90°,点D在第三象限的双曲线y=上,且边AE经过点C.若AB=AD,∠BAD=90°,则k的值为( )
A.3 B.4 C.﹣6 D.6
二、填空题(15分)
16.已知蓄电池的电压为定值,使用蓄电池时,电流(单位:)与电阻(单位:)成反比例函数关系,图像如图所示,则这个反比例函数解析式为_______.
17.在平整的路面上某型号汽车急刹车后仍将滑行的距离s(米)与刹车的速度v(千米/时)有这样的关系,当汽车紧急刹车仍滑行27米时,汽车刹车前的速度是____________千米/时.
18.如图是4个台阶的示意图,每个台阶的高和宽分别是1和2,每个台阶凸出的角的顶点记作(为1~4的整数),函数()的图象为曲线.若曲线使得,这些点分布在它的两侧,每侧各2个点,则的取值范围是______.
19.如图,平面直角坐标系中,在轴上,,点的坐标为,将绕点逆时针旋转,点的对应点恰好落在双曲线上,则的值为_______
20.如图,菱形ABCD的顶点A在x轴的正半轴上,∠C=60°,顶点B,D的纵坐标相同,已知点B的横坐标为7,若过点D的双曲线y=(k>0)恰好过边AB的中点E,则k=_____.
三、解答题(60分)
21.某医药研究所研制了一种新药,在试验药效时发现:成人按规定剂量服用后,检测到从第5分钟起每分钟每毫升血液中含药量增加0.2微克,第100分钟达到最高,接着开始衰退.血液中含药量(微克)与时间(分钟)的函数关系如图.并发现衰退时与成反比例函数关系.
(1) ;
(2)当时,与之间的函数关系式为 ;当时,与之间的函数关系式为 ;
(3)如果每毫升血液中含药量不低于10微克时是有效的,求出一次服药后的有效时间多久?
22.已知直线y=x+t与双曲线y=(k>0)交于C、D两点,过C作CA⊥x轴于点A,过D作DB⊥y轴于点B,连接AB.
(1)求C、D两点的坐标;
(2)试探究直线AB与CD的位置关系并说明理由;
(3)已知点D(3,2),且C、D在抛物线y=ax2+bx+5(a≠0)上,若当m≤x≤n(其中mn<0)时,函数y=ax2+bx+5的最小值为2m,最大值为2n,求m+n的值.
23.定义:若一次函数和反比例函数满足,则称为一次函数和反比例函数的“等差”函数.
(1)和是否存在“等差”函数?若存在,请写出它们的“等差”函数.
(2)若和存在“等差”函数,且“等差”函数的图象与的图象的一个交点的横坐标为1,求反比例函数的表达式.
参考答案
1--10CDACA DBABD 11--15CACBD
16.
17.
18.
19.-3
20.
21.(1);
(2)当时,设与之间的函数关系式为
经过点,
解得:,
解析式为;
当时,与之间的函数关系式为,
经过点,
解得:,
函数的解析式为;
(3)令解得:,
令,解得:
分钟,
服药后能持续135分钟.
22.(1)直线y=x+t与双曲线相交y=,由
得x2+tx﹣k=0,所以x=,
设C(xC,yC),D(xD,yD)
若xC<xD,则C( ),D;
若xC>xD,则,;
(2)AB∥CD,理由如下:
不妨设xC<xD,
由(Ⅰ)知C( ),D;
所以A( ),B(0,).
设直线AB的解析式为y=px+q,
则将A,B两点坐标代入有: +q=0,q= ,所以p=1,
所以直线AB的解析式为y=x+,
所以直线AB与CD的位置关系是AB∥CD.
(3)将D(3,2)代入双曲线 y=(k>0),得k=6,
将D(3,2)代入直线y=x+t,得t=﹣1.∴双曲线:,直线y=x﹣1.
由 ,
得x1=3,x2=﹣2,所以C(﹣2,﹣3).
因为C(﹣2,﹣3),D(3,2)在抛物线y=ax2+bx+5(a≠0)上,所以有: ,
解得 ,即y=﹣x2+2x+5=﹣(x﹣1)2+6.
由mn<0,可知m<0,n>0.
①当0<n≤1时,由函数的最小值为2m,最大值为2n可知 ,
所以m,n即为一元二次方程﹣x2+2x+5=2x的两解 ,
又m<n,所以m=-,n=.
又因为0<n≤1,所以m=-,n=,不合题意.
②当 ≤1,
即m≤2﹣n时,
由函数的最小值为2m,
最大值为2n可知
所以 ,此时m=-≤满足题意.
所以.
③当>1,即m>2﹣n时,由函数的最小值为2m,
最大值为2n可知
所以 ,又因为m<0.
∴m=1,n=3不合题意.
23.(1)存在,
假设一次函数与反比例函数存在“等差”函数,
则,解得,
∴存在“等差”函数,其表达式为.
(2)根据题意知,
∴,
则“等差”函数的表达式为,
反比例函数的表达式为,
根据题意,将代入
得,解得,
故反比例函数的表达式为.
一、单选题(45分)
1.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压是气体体积的反比例函数,其图象如图所示,当气球内的气压大于时气球将爆炸.为了安全起见,气体的体积应满足( )
A. B. C. D.
2.已知长方形的面积为40cm2,相邻两边长分别为xcm和ycm,则y与x之间的函数图象是( )
A. B.
C. D.
3.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压与气体体积之间的函数关系如图所示.当气球的体积是,气球内的气压是( ).
A.96 B.150 C.120 D.64
4.某种气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气球体积V的反比例函数,其图象如图所示,当气球内的气压大于160 kPa时,气球将爆炸,为了安全,气球的体积应该( )
A.不大于m3 B.小于m3 C.不小于m3 D.小于m3
5.如图所示,点B、D在双曲线上,点A在双曲线上,且AD//y轴,AB//x轴, 以AB、AD为邻边作平行四边形ABCD,则平行四边形ABCD的面积是( )
A.4 B.6 C.8 D.10
6.1888年,海因里希 鲁道夫 赫兹证实了电磁波的存在,这成了后来大部分无线科技的基础.电磁波波长λ(单位:米)、频率f(单位:赫兹)满足函数关系λf=3×108,下列说法正确的是( )
A.电磁波波长是频率的正比例函数
B.电磁波波长20000米时,对应的频率1500赫兹
C.电磁波波长小于30000米时,频率小于10000赫兹
D.电磁波波长大于50000米时,频率小于6000赫兹
7.近似眼镜的度数(度)与镜片焦距(米)之间具有如图所示的反比例函数关系,若要配制一副度数小于400度的近似眼镜,则镜片焦距的取值范围是( )
A.0米米 B.米
C.0米米 D.米
8.已知某品牌显示器的使用寿命为定值.这种显示器可工作的天数y与平均每天工作的小时数x是反比例函数关系,图象如图所示.如果这种显示器至少要用2000天,那么显示器平均每天工作的小时数x应控制在( )
A. B. C. D.
9.一辆汽车匀速通过某段公路,所需时间(h)与行驶速度(km/h)满足函数关系点,其图象为如图所示的一段双曲线,端点为和,若行驶速度不得超过60 km/h,则汽车通过该路段最少需要( )
A.分钟 B.40分钟 C.60分钟 D.分钟
10.为了响应“绿水青山就是金山银山”的号召,建设生态文明,某工厂自2019年1月开始限产进行治污改造,其月利润y(万元)与月份x之间的变化如图所示,治污完成前是反比例函数图象的一部分,治污完成后是一次函数图象的一部分,下列选项错误的是( )
A.4月份的利润为50万元
B.治污改造完成后每月利润比前一个月增加30万元
C.治污改造完成前后共有3个月的利润低于100万元
D.8月份该厂利润达到200万元
11.已知:点A是双曲线在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为一边作等边三角形ABC,点C在第四象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式是( )
A. B. C.D.
12.如图,点A是双曲线y=﹣在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为底作等腰△ABC,且∠ACB=120°,点C在第一象限,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=上运动,则k的值为( )
A.3 B.4 C.2.5 D.7
13.如图,一次函数y=ax+b与x轴、y轴交于A、B两点,与反比例函数y=相交于C、D两点,分别过C、D两点作y轴、x轴的垂线,垂足为E、F,连接CF、DE、EF. 有下列三个结论:①△CEF与△DEF的面积相等;②△DCE≌△CDF;③AC=BD.其中正确的结论个数是( )
A.0 B.1 C.2 D.3
14.如图,双曲线y=(k>0)经过矩形OABC的边BC的中点E,交AB于点D,若四边形ODBC的面积为3,则k的值为( )
A.1 B.2 C.3 D.6
15.如图,在平面直角坐标系中,Rt△ABC的顶点A、B的坐标分别为(﹣1,1)、(3,0),直角顶点C在x轴上,在△ADE中,∠E=90°,点D在第三象限的双曲线y=上,且边AE经过点C.若AB=AD,∠BAD=90°,则k的值为( )
A.3 B.4 C.﹣6 D.6
二、填空题(15分)
16.已知蓄电池的电压为定值,使用蓄电池时,电流(单位:)与电阻(单位:)成反比例函数关系,图像如图所示,则这个反比例函数解析式为_______.
17.在平整的路面上某型号汽车急刹车后仍将滑行的距离s(米)与刹车的速度v(千米/时)有这样的关系,当汽车紧急刹车仍滑行27米时,汽车刹车前的速度是____________千米/时.
18.如图是4个台阶的示意图,每个台阶的高和宽分别是1和2,每个台阶凸出的角的顶点记作(为1~4的整数),函数()的图象为曲线.若曲线使得,这些点分布在它的两侧,每侧各2个点,则的取值范围是______.
19.如图,平面直角坐标系中,在轴上,,点的坐标为,将绕点逆时针旋转,点的对应点恰好落在双曲线上,则的值为_______
20.如图,菱形ABCD的顶点A在x轴的正半轴上,∠C=60°,顶点B,D的纵坐标相同,已知点B的横坐标为7,若过点D的双曲线y=(k>0)恰好过边AB的中点E,则k=_____.
三、解答题(60分)
21.某医药研究所研制了一种新药,在试验药效时发现:成人按规定剂量服用后,检测到从第5分钟起每分钟每毫升血液中含药量增加0.2微克,第100分钟达到最高,接着开始衰退.血液中含药量(微克)与时间(分钟)的函数关系如图.并发现衰退时与成反比例函数关系.
(1) ;
(2)当时,与之间的函数关系式为 ;当时,与之间的函数关系式为 ;
(3)如果每毫升血液中含药量不低于10微克时是有效的,求出一次服药后的有效时间多久?
22.已知直线y=x+t与双曲线y=(k>0)交于C、D两点,过C作CA⊥x轴于点A,过D作DB⊥y轴于点B,连接AB.
(1)求C、D两点的坐标;
(2)试探究直线AB与CD的位置关系并说明理由;
(3)已知点D(3,2),且C、D在抛物线y=ax2+bx+5(a≠0)上,若当m≤x≤n(其中mn<0)时,函数y=ax2+bx+5的最小值为2m,最大值为2n,求m+n的值.
23.定义:若一次函数和反比例函数满足,则称为一次函数和反比例函数的“等差”函数.
(1)和是否存在“等差”函数?若存在,请写出它们的“等差”函数.
(2)若和存在“等差”函数,且“等差”函数的图象与的图象的一个交点的横坐标为1,求反比例函数的表达式.
参考答案
1--10CDACA DBABD 11--15CACBD
16.
17.
18.
19.-3
20.
21.(1);
(2)当时,设与之间的函数关系式为
经过点,
解得:,
解析式为;
当时,与之间的函数关系式为,
经过点,
解得:,
函数的解析式为;
(3)令解得:,
令,解得:
分钟,
服药后能持续135分钟.
22.(1)直线y=x+t与双曲线相交y=,由
得x2+tx﹣k=0,所以x=,
设C(xC,yC),D(xD,yD)
若xC<xD,则C( ),D;
若xC>xD,则,;
(2)AB∥CD,理由如下:
不妨设xC<xD,
由(Ⅰ)知C( ),D;
所以A( ),B(0,).
设直线AB的解析式为y=px+q,
则将A,B两点坐标代入有: +q=0,q= ,所以p=1,
所以直线AB的解析式为y=x+,
所以直线AB与CD的位置关系是AB∥CD.
(3)将D(3,2)代入双曲线 y=(k>0),得k=6,
将D(3,2)代入直线y=x+t,得t=﹣1.∴双曲线:,直线y=x﹣1.
由 ,
得x1=3,x2=﹣2,所以C(﹣2,﹣3).
因为C(﹣2,﹣3),D(3,2)在抛物线y=ax2+bx+5(a≠0)上,所以有: ,
解得 ,即y=﹣x2+2x+5=﹣(x﹣1)2+6.
由mn<0,可知m<0,n>0.
①当0<n≤1时,由函数的最小值为2m,最大值为2n可知 ,
所以m,n即为一元二次方程﹣x2+2x+5=2x的两解 ,
又m<n,所以m=-,n=.
又因为0<n≤1,所以m=-,n=,不合题意.
②当 ≤1,
即m≤2﹣n时,
由函数的最小值为2m,
最大值为2n可知
所以 ,此时m=-≤满足题意.
所以.
③当>1,即m>2﹣n时,由函数的最小值为2m,
最大值为2n可知
所以 ,又因为m<0.
∴m=1,n=3不合题意.
23.(1)存在,
假设一次函数与反比例函数存在“等差”函数,
则,解得,
∴存在“等差”函数,其表达式为.
(2)根据题意知,
∴,
则“等差”函数的表达式为,
反比例函数的表达式为,
根据题意,将代入
得,解得,
故反比例函数的表达式为.
