2021-2022学年人教版九年级数学下册26.2实际问题与反比例函数基础测试(word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册26.2实际问题与反比例函数基础测试(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 248.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-29 08:58:59 | ||
图片预览


文档简介
26.2实际问题与反比例函数基础测试卷
一、单选题(45分)
1.已知甲、乙两地相距40米,汽车从甲地匀速行驶到乙地,则汽车行驶时间t(单位:小时)关于行驶速度v(单位:千米/小时)的函数关系式是( )
A.t=40v B. C. D.
2.一个直角三角形的两直角边长分别为x,y,其面积为2,则y与x之间的关系用图象表示大致为( )
A. B.
C. D.
3.平度高铁通车后极大的方便了市民的出行.平度北站建设初期需要运送大量土石方.某运输公司承担了运送总量为106m3土石方的任务,该运输公司平均每天运送土石方的数量v(单位:m3/天)与完成运送任务所需时间t(单位:天)之间的函数关系式是( )
A. B. C. D.
4.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压(kPa)是气体体积()的反比例函数,其图象如图所示,当气体体积为时,气压为( )kPa.
A.150 B.120 C.96 D.84
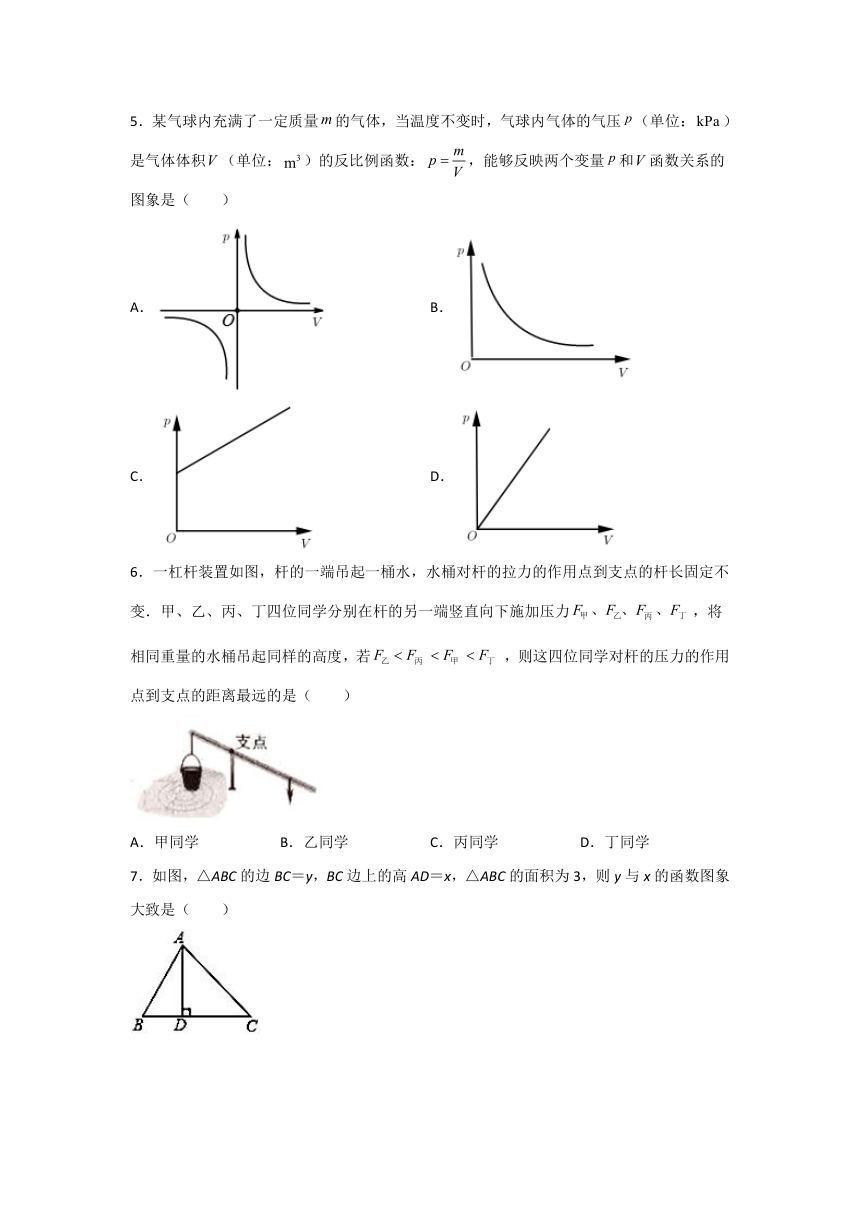
5.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压(单位:)是气体体积(单位:)的反比例函数:,能够反映两个变量和函数关系的图象是( )
A. B.
C. D.
6.一杠杆装置如图,杆的一端吊起一桶水,水桶对杆的拉力的作用点到支点的杆长固定不变.甲、乙、丙、丁四位同学分别在杆的另一端竖直向下施加压力,将相同重量的水桶吊起同样的高度,若,则这四位同学对杆的压力的作用点到支点的距离最远的是( )
A.甲同学 B.乙同学 C.丙同学 D.丁同学
7.如图,△ABC的边BC=y,BC边上的高AD=x,△ABC的面积为3,则y与x的函数图象大致是( )
A. B.
C. D.
8.已知甲、乙两地相距s(km),汽车从甲地匀速行驶到乙地,则汽车行驶的时间t(h)关于行驶速度v(km/h)的函数图像可能是( )
A. B.
C. D.
9.某物体对地面的压力为定值,物体对地面的压强P(pa)与受力面积S(m2)之间的函数关系为P=,如图所示,那么当S>16m2时,P的变化为( )
A.P>10 B.定值 C.逐渐变小 D.无法判断
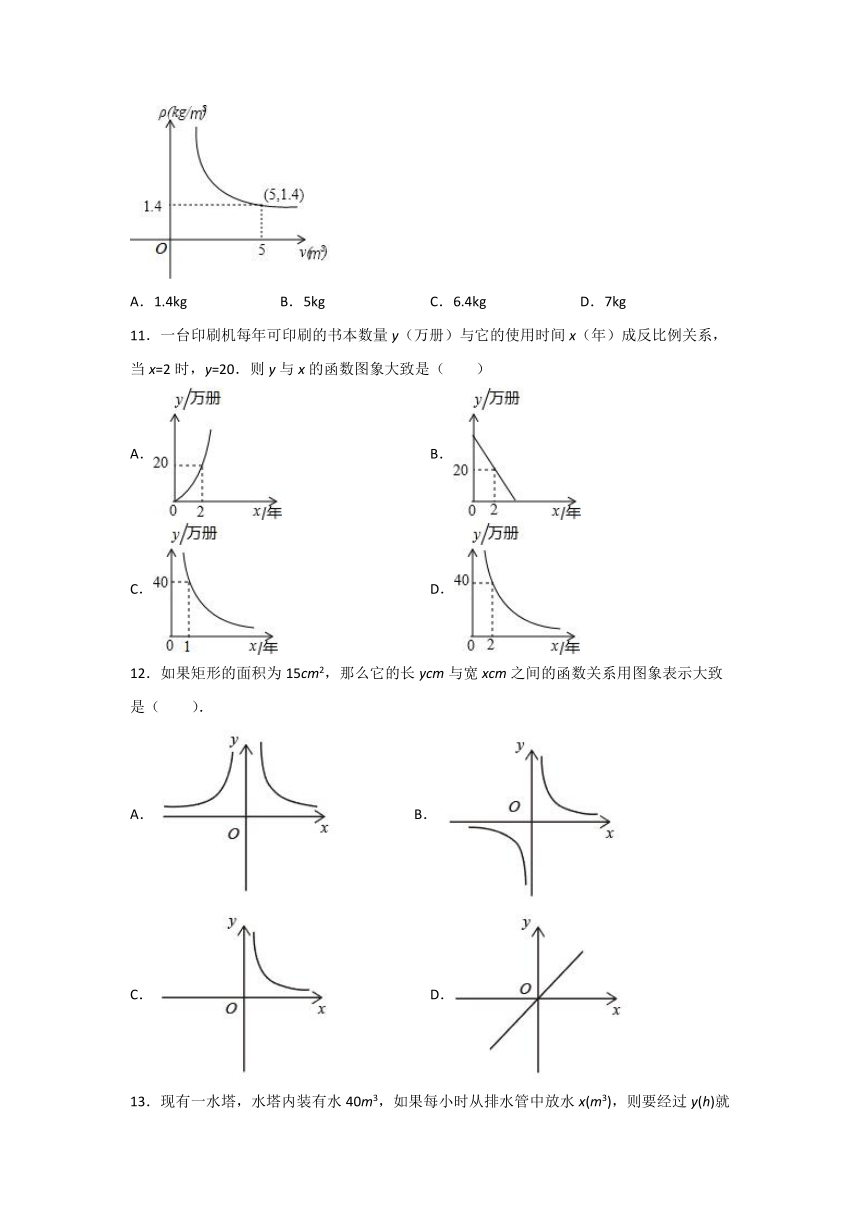
10.在一个可以改变容积的密闭容器内,装有一定质量的某种气体,当改变容积V时,气体的密度也随之改变.与V在一定范围内满足,它的图象如图所示,则该气体的质量m为( ).
A.1.4kg B.5kg C.6.4kg D.7kg
11.一台印刷机每年可印刷的书本数量y(万册)与它的使用时间x(年)成反比例关系,当x=2时,y=20.则y与x的函数图象大致是( )
A. B.
C. D.
12.如果矩形的面积为15cm2,那么它的长ycm与宽xcm之间的函数关系用图象表示大致是( ).
A. B.
C. D.
13.现有一水塔,水塔内装有水40m3,如果每小时从排水管中放水x(m3),则要经过y(h)就可以把水放完该函数的图像大致应是下图中的( )
A. B. C. D.
14.如图,曲线表示温度与时间之间的函数关系,它是一个反比例函数的图象的一支.当温度时,时间应( )
A.不小于 B.不大于 C.不小于 D.不大于
15.如图,在平面直角坐标系中,矩形ABCD的顶点A点,D点分别在x轴、y轴上,对角线BD∥x轴,反比例函数的图象经过矩形对角线的交点E,若点A(2,0),D(0,4),则k的值为( )
A.16 B.20 C.32 D.40
二、填空题(15分)
16.若矩形的面积为2,则矩形相邻两边的长成______比例.
17.列车从甲地驶往乙地.行完全程所需的时间与行驶的平均速度之间的反比例函数关系如图所示.若列车要在内到达,则速度至少需要提高到__________.
18.近视眼镜的度数y(度)与镜片焦距x()成反比例,已知500度的近视眼镜镜片的焦距是,则y与x之间的函数表达式是______.
19.港珠澳大桥全长近55km,汽车行驶完全程所需的时间t(h)与行驶的平均速度v(km/h)之间的关系式为_________.
20.一水桶的下底面积是桶盖面积的2倍,如果将其底朝下放在桌上,它对桌面的压强是500Pa.翻过来放,对桌面的压强是_____________.
三、解答题(60分)
21.为应对全球爆发的新冠疫情,某疫苗生产企业于2021年1月份开始了技术改造,其月生产数量(万支)与月份之间的变化如图所示,技术改造完成前是反比例函数图象的一部分,技术改造完成后是一次函数图象的一部分,请根据图中数据解答下列问题:
(1)该疫苗生产企业4月份的生产数量为多少万支?
(2)该疫苗生产企业有多少个月的月生产数量不超过90万支?
22.为了预防“甲型H1N1”,某学校对教室采用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧后,y与x成反比例,如图所示,现测得药物8min燃毕,此时室内空气每立方米的含药量为6mg,请你根据题中提供的信息,解答下列问题:
(1)药物燃烧时,求y关于x的函数关系式?自变量x的取值范围是什么?药物燃烧后y与x的函数关系式呢?
(2)研究表明,当空气中每立方米的药量低于1.6mg时,学生方可进教室,那么从消毒开始,至少需要几分钟后,学生才能进入教室?
(3)研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10min时,才能杀灭空气中的毒,那么这次消毒是否有效?为什么?
23.某玩具厂生产一种玩具,本着控制固定成本,降价促销的原则,使生产的玩具能够全部售出.据市场调查,若按每个玩具280元销售时,每月可销售300个.若销售单价每降低1元,每月可多售出2个.据统计,每个玩具的固定成本Q(元)与月产销量y(个)满足如下关系:
月产销量y(个) … 160 200 240 300 …
每个玩具的固定成本Q(元) … 60 48 40 32 …
(1)每月产销量y(个)与销售单价x(元)之间的函数关系式为______;从上表可知.每个玩具的固定成本Q(元)与月产销量y(个)之间满足反比例函数关系式,求出Q与y之间的关系式;
(2)若每个玩具的固定成本为30元,求它的销售单价是多少元?
(3)若该厂这种玩具的月产销量不超过400个,求此时销售单价是多少元?
参考答案
1---10BCBCB BACCD 11--15CCCBB
16.反
17.240
18.
19.
20.1000Pa
21.1)该疫苗生产企业4月份的生产数量为45万支;(2)该疫苗生产企业有6个月的月生产数量不超过90万支.
22.(1)药物燃烧时y关于x的函数关系式为y=x(0≤x≤8),药物燃烧后y关于x的函数关系式为y=(x>8);(2)从消毒开始,至少需要30分钟后学生才能进入教室;(3)这次消毒是有效的.
23.(1),;(2)270元;(3)230元
一、单选题(45分)
1.已知甲、乙两地相距40米,汽车从甲地匀速行驶到乙地,则汽车行驶时间t(单位:小时)关于行驶速度v(单位:千米/小时)的函数关系式是( )
A.t=40v B. C. D.
2.一个直角三角形的两直角边长分别为x,y,其面积为2,则y与x之间的关系用图象表示大致为( )
A. B.
C. D.
3.平度高铁通车后极大的方便了市民的出行.平度北站建设初期需要运送大量土石方.某运输公司承担了运送总量为106m3土石方的任务,该运输公司平均每天运送土石方的数量v(单位:m3/天)与完成运送任务所需时间t(单位:天)之间的函数关系式是( )
A. B. C. D.
4.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压(kPa)是气体体积()的反比例函数,其图象如图所示,当气体体积为时,气压为( )kPa.
A.150 B.120 C.96 D.84
5.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压(单位:)是气体体积(单位:)的反比例函数:,能够反映两个变量和函数关系的图象是( )
A. B.
C. D.
6.一杠杆装置如图,杆的一端吊起一桶水,水桶对杆的拉力的作用点到支点的杆长固定不变.甲、乙、丙、丁四位同学分别在杆的另一端竖直向下施加压力,将相同重量的水桶吊起同样的高度,若,则这四位同学对杆的压力的作用点到支点的距离最远的是( )
A.甲同学 B.乙同学 C.丙同学 D.丁同学
7.如图,△ABC的边BC=y,BC边上的高AD=x,△ABC的面积为3,则y与x的函数图象大致是( )
A. B.
C. D.
8.已知甲、乙两地相距s(km),汽车从甲地匀速行驶到乙地,则汽车行驶的时间t(h)关于行驶速度v(km/h)的函数图像可能是( )
A. B.
C. D.
9.某物体对地面的压力为定值,物体对地面的压强P(pa)与受力面积S(m2)之间的函数关系为P=,如图所示,那么当S>16m2时,P的变化为( )
A.P>10 B.定值 C.逐渐变小 D.无法判断
10.在一个可以改变容积的密闭容器内,装有一定质量的某种气体,当改变容积V时,气体的密度也随之改变.与V在一定范围内满足,它的图象如图所示,则该气体的质量m为( ).
A.1.4kg B.5kg C.6.4kg D.7kg
11.一台印刷机每年可印刷的书本数量y(万册)与它的使用时间x(年)成反比例关系,当x=2时,y=20.则y与x的函数图象大致是( )
A. B.
C. D.
12.如果矩形的面积为15cm2,那么它的长ycm与宽xcm之间的函数关系用图象表示大致是( ).
A. B.
C. D.
13.现有一水塔,水塔内装有水40m3,如果每小时从排水管中放水x(m3),则要经过y(h)就可以把水放完该函数的图像大致应是下图中的( )
A. B. C. D.
14.如图,曲线表示温度与时间之间的函数关系,它是一个反比例函数的图象的一支.当温度时,时间应( )
A.不小于 B.不大于 C.不小于 D.不大于
15.如图,在平面直角坐标系中,矩形ABCD的顶点A点,D点分别在x轴、y轴上,对角线BD∥x轴,反比例函数的图象经过矩形对角线的交点E,若点A(2,0),D(0,4),则k的值为( )
A.16 B.20 C.32 D.40
二、填空题(15分)
16.若矩形的面积为2,则矩形相邻两边的长成______比例.
17.列车从甲地驶往乙地.行完全程所需的时间与行驶的平均速度之间的反比例函数关系如图所示.若列车要在内到达,则速度至少需要提高到__________.
18.近视眼镜的度数y(度)与镜片焦距x()成反比例,已知500度的近视眼镜镜片的焦距是,则y与x之间的函数表达式是______.
19.港珠澳大桥全长近55km,汽车行驶完全程所需的时间t(h)与行驶的平均速度v(km/h)之间的关系式为_________.
20.一水桶的下底面积是桶盖面积的2倍,如果将其底朝下放在桌上,它对桌面的压强是500Pa.翻过来放,对桌面的压强是_____________.
三、解答题(60分)
21.为应对全球爆发的新冠疫情,某疫苗生产企业于2021年1月份开始了技术改造,其月生产数量(万支)与月份之间的变化如图所示,技术改造完成前是反比例函数图象的一部分,技术改造完成后是一次函数图象的一部分,请根据图中数据解答下列问题:
(1)该疫苗生产企业4月份的生产数量为多少万支?
(2)该疫苗生产企业有多少个月的月生产数量不超过90万支?
22.为了预防“甲型H1N1”,某学校对教室采用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧后,y与x成反比例,如图所示,现测得药物8min燃毕,此时室内空气每立方米的含药量为6mg,请你根据题中提供的信息,解答下列问题:
(1)药物燃烧时,求y关于x的函数关系式?自变量x的取值范围是什么?药物燃烧后y与x的函数关系式呢?
(2)研究表明,当空气中每立方米的药量低于1.6mg时,学生方可进教室,那么从消毒开始,至少需要几分钟后,学生才能进入教室?
(3)研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10min时,才能杀灭空气中的毒,那么这次消毒是否有效?为什么?
23.某玩具厂生产一种玩具,本着控制固定成本,降价促销的原则,使生产的玩具能够全部售出.据市场调查,若按每个玩具280元销售时,每月可销售300个.若销售单价每降低1元,每月可多售出2个.据统计,每个玩具的固定成本Q(元)与月产销量y(个)满足如下关系:
月产销量y(个) … 160 200 240 300 …
每个玩具的固定成本Q(元) … 60 48 40 32 …
(1)每月产销量y(个)与销售单价x(元)之间的函数关系式为______;从上表可知.每个玩具的固定成本Q(元)与月产销量y(个)之间满足反比例函数关系式,求出Q与y之间的关系式;
(2)若每个玩具的固定成本为30元,求它的销售单价是多少元?
(3)若该厂这种玩具的月产销量不超过400个,求此时销售单价是多少元?
参考答案
1---10BCBCB BACCD 11--15CCCBB
16.反
17.240
18.
19.
20.1000Pa
21.1)该疫苗生产企业4月份的生产数量为45万支;(2)该疫苗生产企业有6个月的月生产数量不超过90万支.
22.(1)药物燃烧时y关于x的函数关系式为y=x(0≤x≤8),药物燃烧后y关于x的函数关系式为y=(x>8);(2)从消毒开始,至少需要30分钟后学生才能进入教室;(3)这次消毒是有效的.
23.(1),;(2)270元;(3)230元
