2021-2022学年华东师大版九年级数学上册第23章 图形的相似单元测试卷 (word版含答案)
文档属性
| 名称 | 2021-2022学年华东师大版九年级数学上册第23章 图形的相似单元测试卷 (word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 590.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-29 10:28:06 | ||
图片预览

文档简介
第23章图形的相似单元测试卷 2021-2022学年华东师大版九年级数学上册
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共9小题,共27分)
下列各组长度的线段(单位:厘米)中,是成比例线段的是( )
A. ,,, B. ,,, C. ,,, D. ,,,
如图,直线abc,则下列结论不正确的为( )
A. B. C. D.
如图所示,小正方形的边长均为1,则下列选项中阴影部分的三角形与ABC相似的是( )
A. B.
C. D.
如图,若点C是线段AB的黄金分割点(AC> BC),则下列结论中正确的是( )
A. B.
C. D.
如图,在 ABCD中,E为CD上一点,连接AE,BE,BD,且AE,BD相交于点F,:=4:25,则DE:EC=( )
A. B.
C. D.
如图,ABO的顶点A在函数y=(x>0)的图象上,ABO=,过AO边的三等分点M,N分别作x轴的平行线交AB于点P,Q.若四边形MNQP的面积为3,则k的值为( )
A. B.
C. D.
如图,在四边形ABCD中,ADBC,对角线AC, BD相交于点O,若AD=1,BC=3,下面四个结论:AO: AC=1:3;ADO∽CBO;:=1:9;若CBO的周长为m,则ADO的周长为3 m,其中正确的是( )
A. B. C. D.
如图,有一块三角形材料ABC,BC=10,高AD=6,把它加工成一个矩形零件,使矩形的一边GH在BC上,其余两个顶点E,F分别在AB,AC上,那么矩形EFHG的周长的取值范围是( )
A. B. C. D.
如图,正方形ABCD的边长为4,延长CB至E使EB=2,以EB为边在上方作正方形EFGB,延长FG交DC于M,连结AM,AF,H为AD的中点,连结FH分别与AB,AM交于点N,K,则下列结论:ANHGNF;AFN=HFG;FN=2NK;:=1:4.其中正确的结论有( )
A. 个 B. 个 C. 个 D. 个
二、填空题(本大题共6小题,共18分)
已知3a-5b=0,则= .
如图,已知ABC,P为AB上一点,连接CP,要使ACP∽ABC,只需添加条件 .(写出一种合适的条件即可)
如图,RtABC中,BCA=,A=, CDAB于D,则CBD与ABC的周长比是 .
如图, 已知ABO的顶点A的坐标为(-2,4),以原点O为位似中心,把ABO的各边缩小到原来的,则与点A对应的点A'的坐标是 .
九年级某班开展数学活动,活动内容为测量如图所示的电线杆AB的高度.在太阳光的照射下,电线杆影子的一部分(BE)落在地面上,另一部分(EF)落在斜坡上,站在水平面上的小明的影子为DG,已知FEH=,CD=1.6 m,DG=0.8 m,BE=2.1 m,EF=1.7 m,则电线杆的高约为 .(结果精确到0.1 m,参考数据:1.41,1.73)
如图,在ABC中,AB=8,AC=16,点P从点A出发,沿AB方向以每秒2个单位长度的速度向点B运动,同时点Q从点C出发,沿CA方向以每秒3个单位长度的速度向点A运动,其中一点到达终点,则另一点也随之停止运动,当ABC与以A,P,Q为顶点的三角形相似时,运动时间为 秒.
三、解答题(本大题共14小题,共75分)
已知===2,且b+d+f0.
(1)求的值;
(2)若a-2c+3e=5,求b-2d+3f的值.
如图,矩形ABCD中,E为BC上一点,连接AE,过顶点D作DF AE,垂足为F,求证:ABE∽DFA.
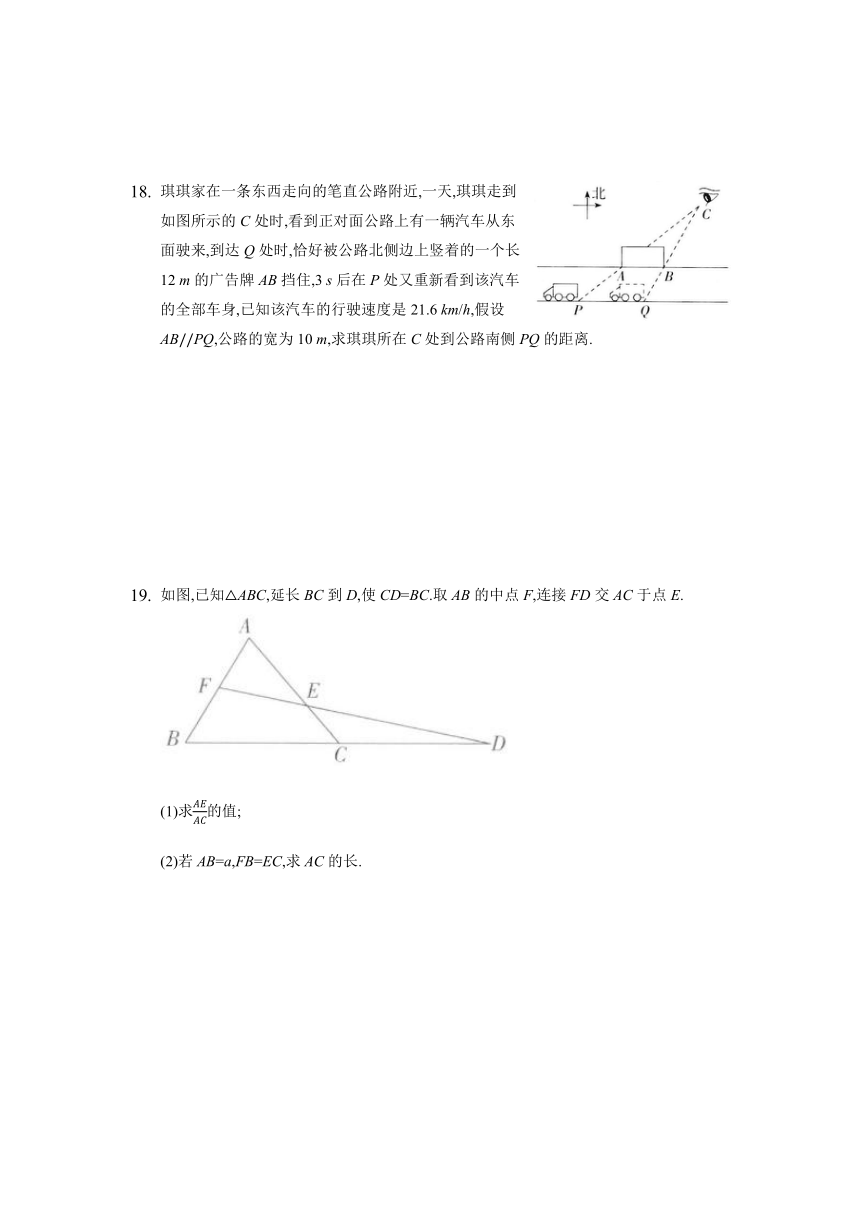
琪琪家在一条东西走向的笔直公路附近,一天,琪琪走到如图所示的C处时,看到正对面公路上有一辆汽车从东面驶来,到达Q处时,恰好被公路北侧边上竖着的一个长12 m的广告牌AB挡住,3 s后在P处又重新看到该汽车的全部车身,已知该汽车的行驶速度是21.6 km/h,假设ABPQ,公路的宽为10 m,求琪琪所在C处到公路南侧PQ的距离.
如图,已知ABC,延长BC到D,使CD=BC.取AB的中点F,连接FD交AC于点E.
(1)求的值;
(2)若AB=a,FB=EC,求AC的长.
现有一块直角三角形木板,它的两条直角边BC,AC分别为3 m和4 m,要把它加工成面积最大的正方形桌面,甲、乙二人的加工方法分别如图和图所示,请运用所学知识说明谁的加工方法符合要求.
如图,在矩形ABCD中,AB=12cm,BC=6cm,点P从点A出发,沿AB边向点B以2cm/s的速度移动,点Q从点D出发,沿DA边向点A以1cm/s的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间(0t6).
(1)当t为何值时,AP=2AQ
(2)计算四边形QAPC的面积,并提出一个与计算结果有关的结论;
(3)当t为何值时,以点Q、A、P为顶点的三角形与ABC相似
阅读下面材料:
小昊遇到这样一个问题:如图1,在ABC中,ACB=,BE是AC边上的中线,点D在BC边上,CD:BD=1:2,AD与BE相交于点P,求的值.
小昊发现,过点A作AFBC,交BE的延长线于点F,通过构造AEF,经过推理和计算能够使问题得到解决(如图2).
请回答:的值为 .
参考小昊思考问题的方法,解决问题:
如图3,在ABC中,ACB=,点D在BC的延长线上,AD与AC边上的中线BE的延长线交于点P,DC:BC:AC=1:2:3.
(1)求的值.
(2)若CD=2,则BP= .
如图,在ABC中,点M为AC边的中点,点E为AB上一点,且AE=AB,连接EM并延长交BC的延长线于点D.求证:BC=2CD.
如图,已知AD是ABC的中线.
(1)若E为AD的中点,射线CE交AB于点F,求;
(2)若E为AD上的一点,且=,射线CE交AB于点F,求.
如图,直线DF分别交ABC的BC,AB两边于D,E,与CA的延长线交于F,若==2,求BE:EA的值.
三角形内角平分线定理:三角形任意两边之比等于它们夹角的平分线分对边之比.已知:如图,在ABC中,AD是角平分线.
求证:=.
如图,在ABC中,ACB=,AC=BC,P是AB上一点,Q是PC上一点(不是中点),MN过点Q且MNCP,分别交AC,BC于点M,N,求证:PA:PB=CM:CN.
如图,在RtABC中,ACB=,CD为斜边AB上的高,E为CD的中点,AE的延长线交BC于点F,FGAB于点G.
求证:=CFBF.
如图,在ABC中,ABAC,AEBC于点E,点D在AC边上,若BD=DC=EC=1,求AC的长.
1.【答案】C
2.【答案】D
3.【答案】A
4.【答案】C
5.【答案】A
6.【答案】D
7.【答案】C
8.【答案】C
9.【答案】C
10.【答案】
11.【答案】ACP=B(答案不唯一)
12.【答案】
13.【答案】(-1,2)或(1,-2)
14.【答案】8.0 m
15.【答案】4或
16.【答案】解:(1)===2,
=2.
(2)===2,
a=2b,c=2d,e=2f,
a-2c+3e=5,
2b-2(2d)+3(2f)=5,
b-2d+3f=2.5.
17.【答案】证明:四边形ABCD是矩形,
ADBC,B=,
DAE=AEB.
DFAE,
DFA=,
B=DFA,
ABE∽DFA.
18.【答案】解: 设琪琪所在C处到公路南侧PQ的距离为x m,
21.6 km/h=6 m/s,
ABPQ,
CAB∽CPQ,
=,
=,
x=30,
琪琪所在C处到公路南侧PQ的距离为30 m.
19.【答案】解析 (1)取BC中点M,连接FM,
F为AB的中点,
FM=AC,FMAC.
CED=MFD,ECD=FMD.
FMD∽ECD.
又DC=BC,
==.
EC=FM=AC=AC.
===.
(2)AB=a,
FB=AB=a.
FB=EC,
EC=a.
EC=AC,
AC=3EC=a.
20.【答案】解:设甲加工的桌面边长为x m.
FDBC,
RtAFD RtACB.
=,即=,解得x=.
设乙加工的桌面边长为y m,如图,过点C作CMAB,垂足为M,CM交GF于点N,
在RtABC中,BC=3 m,AC=4 m,
AB==5(m).
ACBC=CMAB,
CM== m.
GFAB,
GCF ACB.
=,即=,
解得y=.
>,
x>y,>.
甲的加工面积最大,符合要求.
21.【答案】解:(1)由题意得,AP=2tcm,DQ=tcm,QA=(6-t)cm.
当AP=2AQ时,即2t=2(6-t),解得t=3,
当t=3时,AP=2AQ.
(2)在CPB中,BP=(12-2t)cm,
=--=126-12t-6(12-2t)=36().
由计算结果发现:四边形QAPC的面积始终保持不变.
(3)可分为两种情况:
当=时,AQP∽BCA,那么有=,解得t=3,
即当t=3时,AQP∽BCA;
当=时,AQP∽BAC,那么有=,解得t=1.2,
即当t=1.2时,AQP∽BAC.
综上,当t=1.2或3时,以点Q,A,P为顶点的三角形与ABC相似.
22.【答案】解: 的值为
(1)过点A作AFDB,交BE的延长线于点F,
设DC=k,由DC:BC=1:2得BC=2k,DB=DC+BC=3k.
E是AC中点,
AE=CE.
AFDB,
F=DBE.
在AEF和CEB中,
AEF CEB(AAS).
AF=BC=2k.
AFDB,
AFP∽DBP.
===.
的值为.
(2)6
23.【答案】证明:方法一:如图,过点C作CFAB,交DE于点F,
FCD=B.
又D为公共角,
CDF∽BDE.
=.
点M为AC边的中点,
AM=CM.
CFAB,
A=MCF.
又AME=CMF,
AMECMF.
AE=CF.
AE=AB,BE=AB-AE,
BE=3AE.=.
=,
==,即BD=3CD.
又BD=BC+CD,
BC=2CD.
方法二:如图,过点C作CFDE,交AB于点F,
=.
又点M为AC边的中点,
AC=2AM.
2AE=AF.AE=EF.
又=,=2.
又CFDE,==2.
BC=2CD.
方法三:如图,过点E作EFBC,交AC于点F,
AEF=B.
又A为公共角,
AEF∽ABC.
==.
由AE=AB,知
===,
EF=BC,AF=AC.
由EFCD,易证得EFM∽DCM,
=.
又AM=MC,MF=MC.
EF=CD.
BC=2CD.
方法四:如图,过点A作AFBD,交DE的延长线于点F,
F=D,FAE=B.
AEF∽BED.
=.
AE=AB,
AE=BE.AF=BD.
由AFCD,易证得AFM∽CDM.
又AM=MC,AF=CD.
CD=BD.BC=2CD.
24.【答案】解:如图,过点D作DGCF交AB于点G.
(1)DGCF,
=.
又AD是ABC的中线,
BD=DC.BG=GF.
DGCF,
=.
又E为AD的中点,
AE=ED.AF=GF.
AF=FG=GB.=.
(2)DGCF,=.
又=,=,即FG=kAF.
由(1)知BG=GF,BG=FG=kAF.
BF=2kAF.=.
25.【答案】解:如图,过点D作AB的平行线交AC于G.
==2,
=,=.
易得FAE∽FGD,CGD∽CAB.
==,==.
AE=DG,AB=3DG,
BE=DG,
BE:AE=7:2=.
26.【答案】证明:如图,过点C作CEDA,交BA的延长线于点E.
1=E,2=3.
AD是ABC的角平分线,
1=2.
3=E.
AC=AE.
又ADCE,
=.
=.
27.【答案】证明:过点P作PEAC于E,PFCB于F,则四边形CEPF为矩形.
PF=EC.
易得A=B=,AEP=BFP=,
AEP∽BFP.
=.
=.
CPMN于Q,
QCN+QNC=.
又QCN+QCM=,
QCM=QNC.
又PEC=MCN=,PEC∽MCN.
=,即=.
由得=,即PA:PB=CM:CN.
28.【答案】证明:延长GF与AC,交于点H,
CDAB,FGAB,
CDFG,AGF=ADE=,
AFG=AED,AHF=ACE,AFH=AEC.
AFG∽AED,AFH∽AEC.
=,=.
=.
又ED=EC,FG=FH.
HCF=BGF=,CFH=GFB,
CFH∽GFB,
=FGFH=CFBF.
FG=FH,=CFBF.
29.【答案】解:取BC的中点M,连接AM.
ABAC,AM=CM,
MAC=C.
BD=DC,DBC=C.
MAC=DBC.
又C=C,
MAC∽DBC.
=.
又DC=1,MC=BC,
AC==.
易得RtAEC∽RtBAC,
=,
又EC=1,
=CEBC=BC.
由得,AC=,AC=.
第2页,共3页
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共9小题,共27分)
下列各组长度的线段(单位:厘米)中,是成比例线段的是( )
A. ,,, B. ,,, C. ,,, D. ,,,
如图,直线abc,则下列结论不正确的为( )
A. B. C. D.
如图所示,小正方形的边长均为1,则下列选项中阴影部分的三角形与ABC相似的是( )
A. B.
C. D.
如图,若点C是线段AB的黄金分割点(AC> BC),则下列结论中正确的是( )
A. B.
C. D.
如图,在 ABCD中,E为CD上一点,连接AE,BE,BD,且AE,BD相交于点F,:=4:25,则DE:EC=( )
A. B.
C. D.
如图,ABO的顶点A在函数y=(x>0)的图象上,ABO=,过AO边的三等分点M,N分别作x轴的平行线交AB于点P,Q.若四边形MNQP的面积为3,则k的值为( )
A. B.
C. D.
如图,在四边形ABCD中,ADBC,对角线AC, BD相交于点O,若AD=1,BC=3,下面四个结论:AO: AC=1:3;ADO∽CBO;:=1:9;若CBO的周长为m,则ADO的周长为3 m,其中正确的是( )
A. B. C. D.
如图,有一块三角形材料ABC,BC=10,高AD=6,把它加工成一个矩形零件,使矩形的一边GH在BC上,其余两个顶点E,F分别在AB,AC上,那么矩形EFHG的周长的取值范围是( )
A. B. C. D.
如图,正方形ABCD的边长为4,延长CB至E使EB=2,以EB为边在上方作正方形EFGB,延长FG交DC于M,连结AM,AF,H为AD的中点,连结FH分别与AB,AM交于点N,K,则下列结论:ANHGNF;AFN=HFG;FN=2NK;:=1:4.其中正确的结论有( )
A. 个 B. 个 C. 个 D. 个
二、填空题(本大题共6小题,共18分)
已知3a-5b=0,则= .
如图,已知ABC,P为AB上一点,连接CP,要使ACP∽ABC,只需添加条件 .(写出一种合适的条件即可)
如图,RtABC中,BCA=,A=, CDAB于D,则CBD与ABC的周长比是 .
如图, 已知ABO的顶点A的坐标为(-2,4),以原点O为位似中心,把ABO的各边缩小到原来的,则与点A对应的点A'的坐标是 .
九年级某班开展数学活动,活动内容为测量如图所示的电线杆AB的高度.在太阳光的照射下,电线杆影子的一部分(BE)落在地面上,另一部分(EF)落在斜坡上,站在水平面上的小明的影子为DG,已知FEH=,CD=1.6 m,DG=0.8 m,BE=2.1 m,EF=1.7 m,则电线杆的高约为 .(结果精确到0.1 m,参考数据:1.41,1.73)
如图,在ABC中,AB=8,AC=16,点P从点A出发,沿AB方向以每秒2个单位长度的速度向点B运动,同时点Q从点C出发,沿CA方向以每秒3个单位长度的速度向点A运动,其中一点到达终点,则另一点也随之停止运动,当ABC与以A,P,Q为顶点的三角形相似时,运动时间为 秒.
三、解答题(本大题共14小题,共75分)
已知===2,且b+d+f0.
(1)求的值;
(2)若a-2c+3e=5,求b-2d+3f的值.
如图,矩形ABCD中,E为BC上一点,连接AE,过顶点D作DF AE,垂足为F,求证:ABE∽DFA.
琪琪家在一条东西走向的笔直公路附近,一天,琪琪走到如图所示的C处时,看到正对面公路上有一辆汽车从东面驶来,到达Q处时,恰好被公路北侧边上竖着的一个长12 m的广告牌AB挡住,3 s后在P处又重新看到该汽车的全部车身,已知该汽车的行驶速度是21.6 km/h,假设ABPQ,公路的宽为10 m,求琪琪所在C处到公路南侧PQ的距离.
如图,已知ABC,延长BC到D,使CD=BC.取AB的中点F,连接FD交AC于点E.
(1)求的值;
(2)若AB=a,FB=EC,求AC的长.
现有一块直角三角形木板,它的两条直角边BC,AC分别为3 m和4 m,要把它加工成面积最大的正方形桌面,甲、乙二人的加工方法分别如图和图所示,请运用所学知识说明谁的加工方法符合要求.
如图,在矩形ABCD中,AB=12cm,BC=6cm,点P从点A出发,沿AB边向点B以2cm/s的速度移动,点Q从点D出发,沿DA边向点A以1cm/s的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间(0t6).
(1)当t为何值时,AP=2AQ
(2)计算四边形QAPC的面积,并提出一个与计算结果有关的结论;
(3)当t为何值时,以点Q、A、P为顶点的三角形与ABC相似
阅读下面材料:
小昊遇到这样一个问题:如图1,在ABC中,ACB=,BE是AC边上的中线,点D在BC边上,CD:BD=1:2,AD与BE相交于点P,求的值.
小昊发现,过点A作AFBC,交BE的延长线于点F,通过构造AEF,经过推理和计算能够使问题得到解决(如图2).
请回答:的值为 .
参考小昊思考问题的方法,解决问题:
如图3,在ABC中,ACB=,点D在BC的延长线上,AD与AC边上的中线BE的延长线交于点P,DC:BC:AC=1:2:3.
(1)求的值.
(2)若CD=2,则BP= .
如图,在ABC中,点M为AC边的中点,点E为AB上一点,且AE=AB,连接EM并延长交BC的延长线于点D.求证:BC=2CD.
如图,已知AD是ABC的中线.
(1)若E为AD的中点,射线CE交AB于点F,求;
(2)若E为AD上的一点,且=,射线CE交AB于点F,求.
如图,直线DF分别交ABC的BC,AB两边于D,E,与CA的延长线交于F,若==2,求BE:EA的值.
三角形内角平分线定理:三角形任意两边之比等于它们夹角的平分线分对边之比.已知:如图,在ABC中,AD是角平分线.
求证:=.
如图,在ABC中,ACB=,AC=BC,P是AB上一点,Q是PC上一点(不是中点),MN过点Q且MNCP,分别交AC,BC于点M,N,求证:PA:PB=CM:CN.
如图,在RtABC中,ACB=,CD为斜边AB上的高,E为CD的中点,AE的延长线交BC于点F,FGAB于点G.
求证:=CFBF.
如图,在ABC中,ABAC,AEBC于点E,点D在AC边上,若BD=DC=EC=1,求AC的长.
1.【答案】C
2.【答案】D
3.【答案】A
4.【答案】C
5.【答案】A
6.【答案】D
7.【答案】C
8.【答案】C
9.【答案】C
10.【答案】
11.【答案】ACP=B(答案不唯一)
12.【答案】
13.【答案】(-1,2)或(1,-2)
14.【答案】8.0 m
15.【答案】4或
16.【答案】解:(1)===2,
=2.
(2)===2,
a=2b,c=2d,e=2f,
a-2c+3e=5,
2b-2(2d)+3(2f)=5,
b-2d+3f=2.5.
17.【答案】证明:四边形ABCD是矩形,
ADBC,B=,
DAE=AEB.
DFAE,
DFA=,
B=DFA,
ABE∽DFA.
18.【答案】解: 设琪琪所在C处到公路南侧PQ的距离为x m,
21.6 km/h=6 m/s,
ABPQ,
CAB∽CPQ,
=,
=,
x=30,
琪琪所在C处到公路南侧PQ的距离为30 m.
19.【答案】解析 (1)取BC中点M,连接FM,
F为AB的中点,
FM=AC,FMAC.
CED=MFD,ECD=FMD.
FMD∽ECD.
又DC=BC,
==.
EC=FM=AC=AC.
===.
(2)AB=a,
FB=AB=a.
FB=EC,
EC=a.
EC=AC,
AC=3EC=a.
20.【答案】解:设甲加工的桌面边长为x m.
FDBC,
RtAFD RtACB.
=,即=,解得x=.
设乙加工的桌面边长为y m,如图,过点C作CMAB,垂足为M,CM交GF于点N,
在RtABC中,BC=3 m,AC=4 m,
AB==5(m).
ACBC=CMAB,
CM== m.
GFAB,
GCF ACB.
=,即=,
解得y=.
>,
x>y,>.
甲的加工面积最大,符合要求.
21.【答案】解:(1)由题意得,AP=2tcm,DQ=tcm,QA=(6-t)cm.
当AP=2AQ时,即2t=2(6-t),解得t=3,
当t=3时,AP=2AQ.
(2)在CPB中,BP=(12-2t)cm,
=--=126-12t-6(12-2t)=36().
由计算结果发现:四边形QAPC的面积始终保持不变.
(3)可分为两种情况:
当=时,AQP∽BCA,那么有=,解得t=3,
即当t=3时,AQP∽BCA;
当=时,AQP∽BAC,那么有=,解得t=1.2,
即当t=1.2时,AQP∽BAC.
综上,当t=1.2或3时,以点Q,A,P为顶点的三角形与ABC相似.
22.【答案】解: 的值为
(1)过点A作AFDB,交BE的延长线于点F,
设DC=k,由DC:BC=1:2得BC=2k,DB=DC+BC=3k.
E是AC中点,
AE=CE.
AFDB,
F=DBE.
在AEF和CEB中,
AEF CEB(AAS).
AF=BC=2k.
AFDB,
AFP∽DBP.
===.
的值为.
(2)6
23.【答案】证明:方法一:如图,过点C作CFAB,交DE于点F,
FCD=B.
又D为公共角,
CDF∽BDE.
=.
点M为AC边的中点,
AM=CM.
CFAB,
A=MCF.
又AME=CMF,
AMECMF.
AE=CF.
AE=AB,BE=AB-AE,
BE=3AE.=.
=,
==,即BD=3CD.
又BD=BC+CD,
BC=2CD.
方法二:如图,过点C作CFDE,交AB于点F,
=.
又点M为AC边的中点,
AC=2AM.
2AE=AF.AE=EF.
又=,=2.
又CFDE,==2.
BC=2CD.
方法三:如图,过点E作EFBC,交AC于点F,
AEF=B.
又A为公共角,
AEF∽ABC.
==.
由AE=AB,知
===,
EF=BC,AF=AC.
由EFCD,易证得EFM∽DCM,
=.
又AM=MC,MF=MC.
EF=CD.
BC=2CD.
方法四:如图,过点A作AFBD,交DE的延长线于点F,
F=D,FAE=B.
AEF∽BED.
=.
AE=AB,
AE=BE.AF=BD.
由AFCD,易证得AFM∽CDM.
又AM=MC,AF=CD.
CD=BD.BC=2CD.
24.【答案】解:如图,过点D作DGCF交AB于点G.
(1)DGCF,
=.
又AD是ABC的中线,
BD=DC.BG=GF.
DGCF,
=.
又E为AD的中点,
AE=ED.AF=GF.
AF=FG=GB.=.
(2)DGCF,=.
又=,=,即FG=kAF.
由(1)知BG=GF,BG=FG=kAF.
BF=2kAF.=.
25.【答案】解:如图,过点D作AB的平行线交AC于G.
==2,
=,=.
易得FAE∽FGD,CGD∽CAB.
==,==.
AE=DG,AB=3DG,
BE=DG,
BE:AE=7:2=.
26.【答案】证明:如图,过点C作CEDA,交BA的延长线于点E.
1=E,2=3.
AD是ABC的角平分线,
1=2.
3=E.
AC=AE.
又ADCE,
=.
=.
27.【答案】证明:过点P作PEAC于E,PFCB于F,则四边形CEPF为矩形.
PF=EC.
易得A=B=,AEP=BFP=,
AEP∽BFP.
=.
=.
CPMN于Q,
QCN+QNC=.
又QCN+QCM=,
QCM=QNC.
又PEC=MCN=,PEC∽MCN.
=,即=.
由得=,即PA:PB=CM:CN.
28.【答案】证明:延长GF与AC,交于点H,
CDAB,FGAB,
CDFG,AGF=ADE=,
AFG=AED,AHF=ACE,AFH=AEC.
AFG∽AED,AFH∽AEC.
=,=.
=.
又ED=EC,FG=FH.
HCF=BGF=,CFH=GFB,
CFH∽GFB,
=FGFH=CFBF.
FG=FH,=CFBF.
29.【答案】解:取BC的中点M,连接AM.
ABAC,AM=CM,
MAC=C.
BD=DC,DBC=C.
MAC=DBC.
又C=C,
MAC∽DBC.
=.
又DC=1,MC=BC,
AC==.
易得RtAEC∽RtBAC,
=,
又EC=1,
=CEBC=BC.
由得,AC=,AC=.
第2页,共3页
