2021-2022学年人教版九年级数学下册第27章相似 单元达标测试 (word版含解析)
文档属性
| 名称 | 2021-2022学年人教版九年级数学下册第27章相似 单元达标测试 (word版含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 332.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-29 00:00:00 | ||
图片预览


文档简介
2021-2022学年人教版九年级数学下册《第27章相似》单元达标测试(附答案)
一.选择题(共10小题,满分40分)
1.已知,则等于( )
A. B. C.2 D.3
2.如图,用图中的数据不能组成的比例是( )
A.2:4=1.5:3 B.3:1.5=4:2 C.2:3=1.5:4 D.1.5:2=3:4
3.点P是长度为1的线段上的黄金分割点,则较短线段的长度为( )
A. B. C. D.
4.将一个四边形放在2倍的放大镜下,则下列说法不正确的是( )
A.四边形的边长扩大为原来的2倍
B.四边形的各角扩大为原来的2倍
C.四边形的周长扩大为原来的2倍
D.四边形的面积扩大为原来的4倍
5.如图,在△ABC中,AD∥BC,点E在AB边上,EF∥BC,交AC边于点F,DE交AC边于点G,则下列结论中错误的是( )
A. B. C. D.
6.已知点P是线段AB的黄金分割点,AP>BP.记以AP为一边的正方形面积为S1,以BP、AB为邻边矩形的面积为S2,则( )
A.S1>S2 B.S1=S2
C.S1<S2 D.S1、S2大小不能确定
7.如图,AD是△ABC的中线,点E在AD上,AD=4DE,连接BE并延长交AC于点F,则AF:FC的值是( )
A.3:2 B.4:3 C.2:1 D.2:3
8.如图,点D、E分别在△ABC的边AB、AC上,且AB=9,AC=6,AD=3,若使△ADE与△ABC相似,则AE的长为( )
A.2 B. C.2或 D.3或
9.如图是用卡钳测量容器内径的示意图,现量得卡钳上A,D两个端点之间的距离为10cm,==,则容器的内径是( )
A.5cm B.10cm C.15cm D.20cm
10.如图,在直角坐标系中,有一等腰直角三角形OBA,∠OAB=90°,直角边OA在x轴正半轴上,且OA=1,将Rt△OBA绕原点O顺时针旋转90°,同时扩大边长的1倍,得到等腰直角三角形OB1A1(即A1O=2AO).同理,将Rt△OB1A1顺时针旋转90°,同时扩大边长1倍,得到等腰直角三角形OB2A2……依此规律,得到等腰直角三角形OB2019A2019,则点B2019的坐标为( )
A.(﹣22019,22019) B.(22019,﹣22019) C.(﹣22018,22018) D.(22018,﹣22018)
二.填空题(共6小题,满分24分)
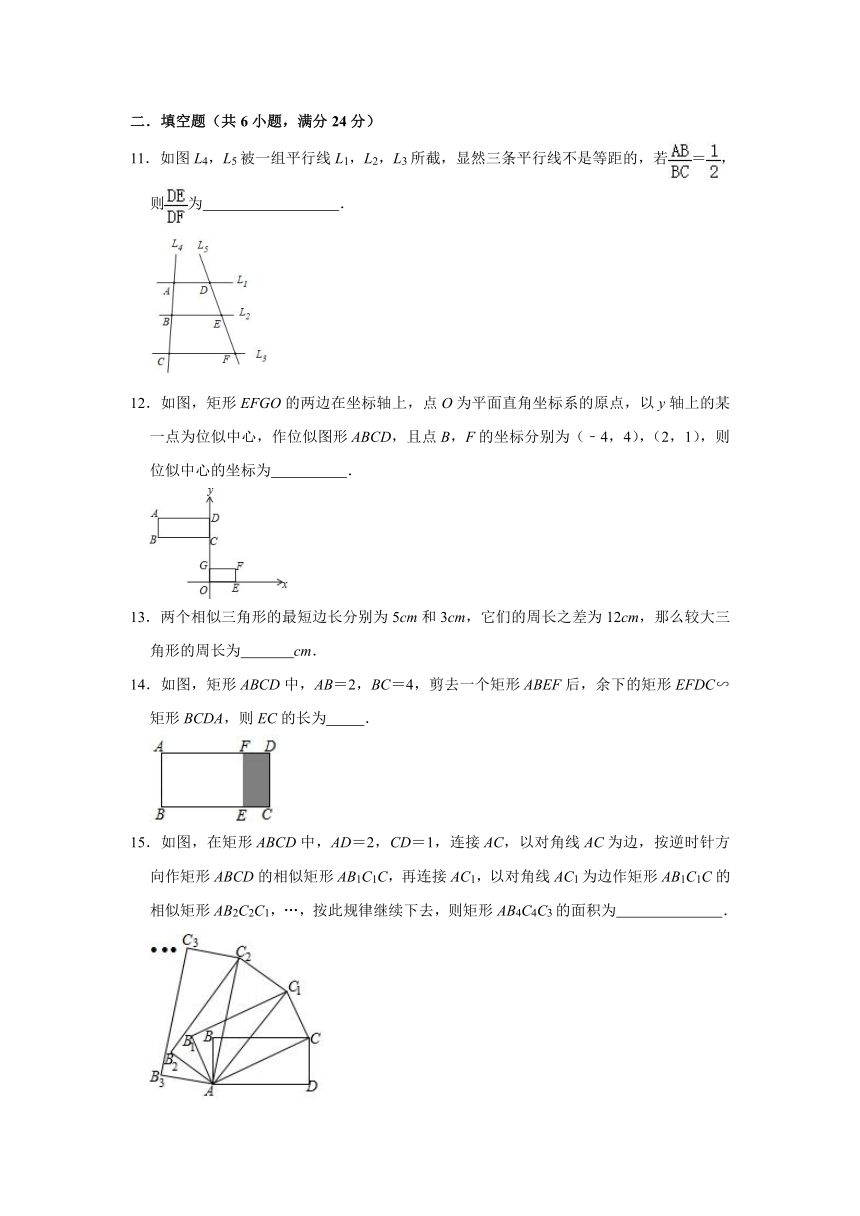
11.如图L4,L5被一组平行线L1,L2,L3所截,显然三条平行线不是等距的,若=,则为 .
12.如图,矩形EFGO的两边在坐标轴上,点O为平面直角坐标系的原点,以y轴上的某一点为位似中心,作位似图形ABCD,且点B,F的坐标分别为(﹣4,4),(2,1),则位似中心的坐标为 .
13.两个相似三角形的最短边长分别为5cm和3cm,它们的周长之差为12cm,那么较大三角形的周长为 cm.
14.如图,矩形ABCD中,AB=2,BC=4,剪去一个矩形ABEF后,余下的矩形EFDC∽矩形BCDA,则EC的长为 .
15.如图,在矩形ABCD中,AD=2,CD=1,连接AC,以对角线AC为边,按逆时针方向作矩形ABCD的相似矩形AB1C1C,再连接AC1,以对角线AC1为边作矩形AB1C1C的相似矩形AB2C2C1,…,按此规律继续下去,则矩形AB4C4C3的面积为 .
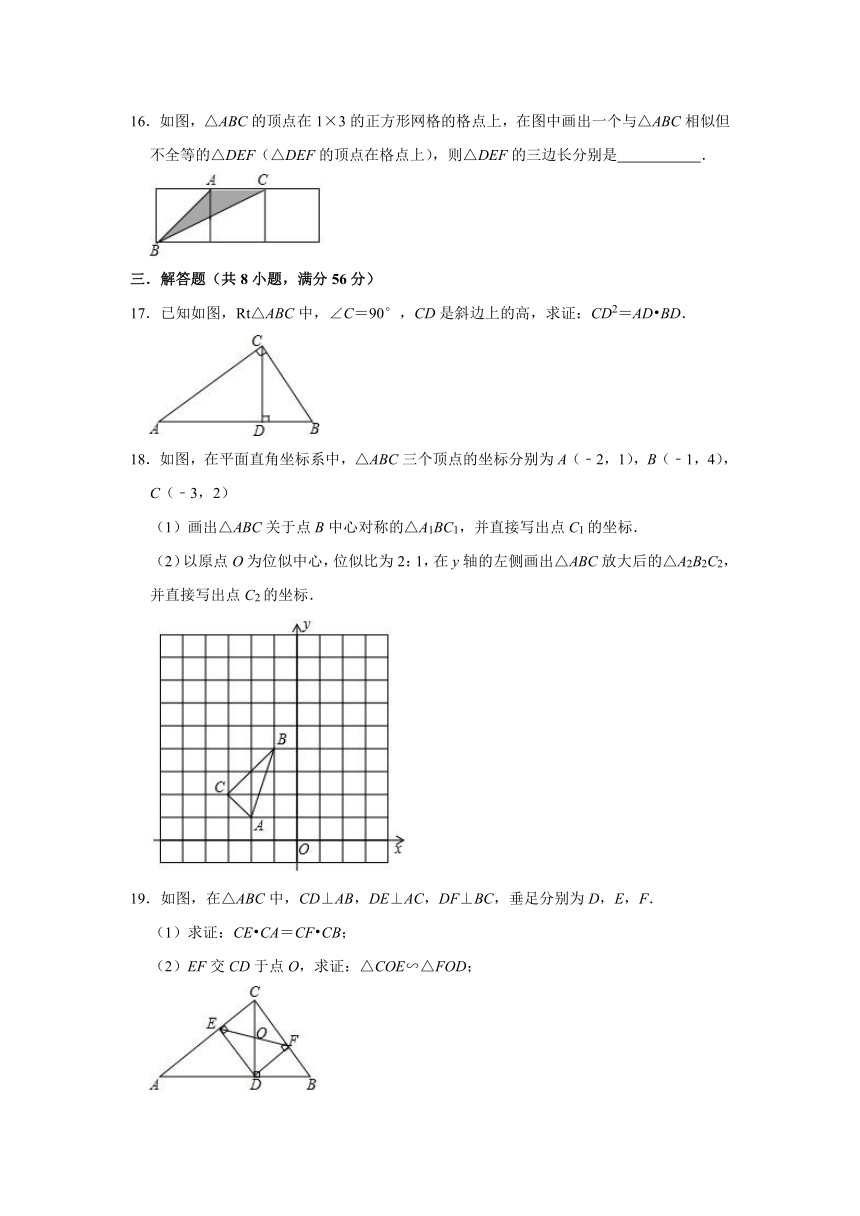
16.如图,△ABC的顶点在1×3的正方形网格的格点上,在图中画出一个与△ABC相似但不全等的△DEF(△DEF的顶点在格点上),则△DEF的三边长分别是 .
三.解答题(共8小题,满分56分)
17.已知如图,Rt△ABC中,∠C=90°,CD是斜边上的高,求证:CD2=AD BD.
18.如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(﹣2,1),B(﹣1,4),C(﹣3,2)
(1)画出△ABC关于点B中心对称的△A1BC1,并直接写出点C1的坐标.
(2)以原点O为位似中心,位似比为2:1,在y轴的左侧画出△ABC放大后的△A2B2C2,并直接写出点C2的坐标.
19.如图,在△ABC中,CD⊥AB,DE⊥AC,DF⊥BC,垂足分别为D,E,F.
(1)求证:CE CA=CF CB;
(2)EF交CD于点O,求证:△COE∽△FOD;
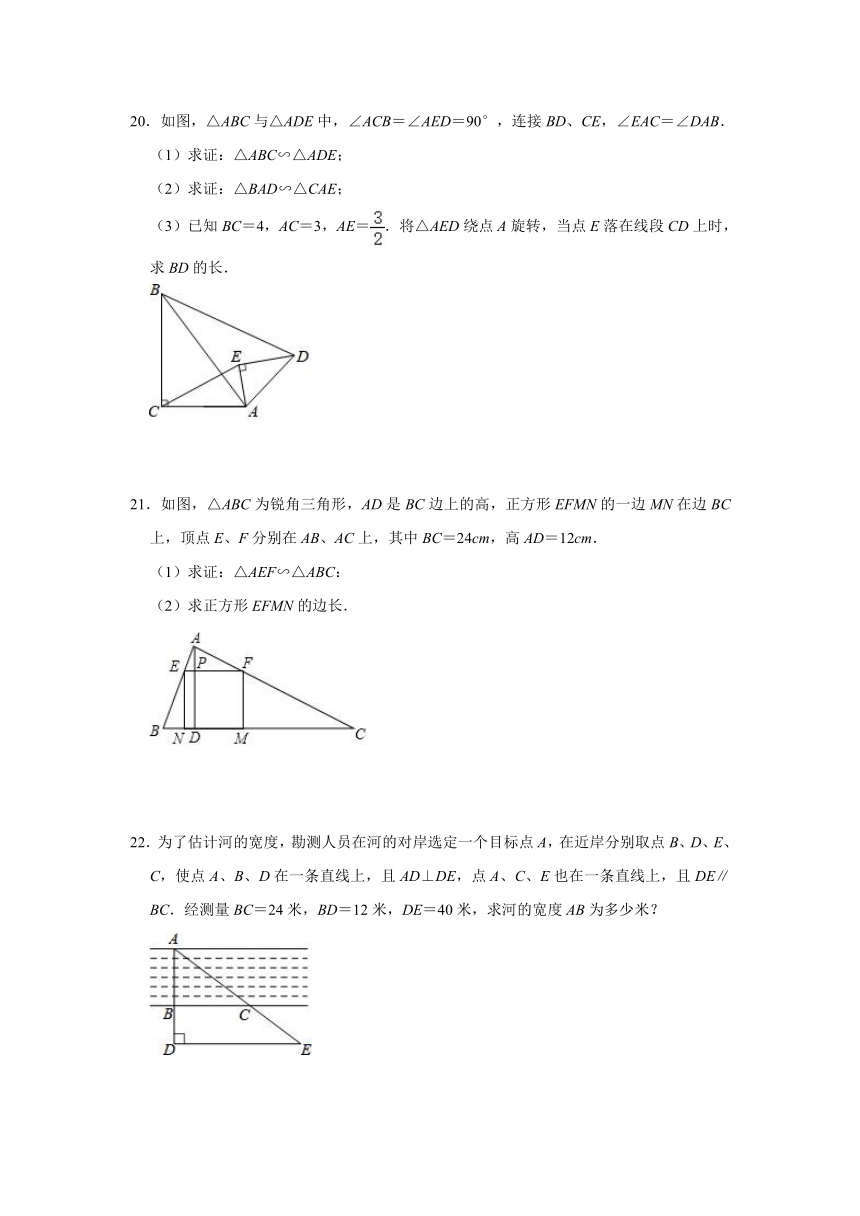
20.如图,△ABC与△ADE中,∠ACB=∠AED=90°,连接BD、CE,∠EAC=∠DAB.
(1)求证:△ABC∽△ADE;
(2)求证:△BAD∽△CAE;
(3)已知BC=4,AC=3,AE=.将△AED绕点A旋转,当点E落在线段CD上时,求BD的长.
21.如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFMN的一边MN在边BC上,顶点E、F分别在AB、AC上,其中BC=24cm,高AD=12cm.
(1)求证:△AEF∽△ABC:
(2)求正方形EFMN的边长.
22.为了估计河的宽度,勘测人员在河的对岸选定一个目标点A,在近岸分别取点B、D、E、C,使点A、B、D在一条直线上,且AD⊥DE,点A、C、E也在一条直线上,且DE∥BC.经测量BC=24米,BD=12米,DE=40米,求河的宽度AB为多少米?
23.已知在平行四边形ABCD中,过点D作DE⊥BC于点E,且AD=DE.连接AC交DE于点F,作DG⊥AC于点G.
(1)如图1,若,AF=,求DG的长;
(2)如图2,作EM⊥AC于点M,连接DM,求证:AM﹣EM=2DG.
24.如图,矩形ABCD中,E是BC上一点,点F是点E关于点C的对称点,过点F作对角线BD的平行线,交DC的延长线于点H,连接HE并延长与矩形的边AB、对角线BD于点N、M.
(1)试判定△BME的形状,并说明理由.
(2)若BE=2EC,连接DE,当△MED为直角三角形时,求AB:BC的值.
参考答案
一.选择题(共10小题,满分40分)
1.解:∵,
∴y=2x,
∴==.
故选:A.
2.解:A、2:4=1:2=1.5:3,能组成比例,错误;
B、3:1.5=2:1=4:2,能组成比例,错误;
C、2:3≠1.5:4;不能组成比例,正确;
D、1.5:2=3:4,能组成比例,错误;
故选:C.
3.解:较短线段的长度=1﹣×1
=,
故选:C.
4.解:放大前后的多边形按照比例放大与缩小,因此它们是相似多边形,放大后的倍数就是相似比,
∴选项:A,C,D正确,
故选:B.
5.解:∵EF∥BC
∴,∴答案A正确;
根据合比性质,则有
即:,∴答案D正确;
又∵AD∥EF
∴,∴答案B正确;
而,∴答案C错误.
故选:C.
6.解:根据黄金分割的概念得:AP:AB=PB:AP,即AP2=PB AB,
则S1:S2=AP2:(PB AB)=1,即S1=S2.
故选:B.
7.解:过点D作DG∥AC,与BF交于点G.
∵AD=4DE,
∴AE=3DE,
∵AD是△ABC的中线,
∴,
∴,即AF=3DG
∴,即FC=2DG,
∴AF:FC=3DG:2DG=3:2.
故选:A.
8.解:①若∠AED对应∠B时,=,即=,
解得AE=;
②当∠ADE对应∠B时,=,即=,
解得AE=2.
故选:C.
9.解:如图,连接AD,BC,
∵,∠AOD=∠BOC,
∴△AOD∽△BOC,
∴==,
又AD=10cm,
∴BC=2AD=20cm.
故选:D.
10.解:∵△AOB是等腰直角三角形,OA=1,
∴AB=OA=1,
∴B(1,1),
将Rt△AOB绕原点O顺时针旋转90°得到等腰直角三角形A1OB1,且A1O=2AO,
再将Rt△A1OB1绕原点O顺时针旋转90°得到等腰直角三角形A2OB2,且A2O=2A1O…,依此规律,
∴每4次循环一周,B1(2,﹣2),B2(﹣4,﹣4),B3(﹣8,8),B4(16,16),
∵2019÷4=502…3,
∴点B2019与B3同在一个象限内,
∵﹣4=﹣22,8=23,16=24,
∴点B2019(﹣22019,22019).
故选:A.
二.填空题(共6小题,满分24分)
11.解:∵L1∥L2∥L3,
∴=,
∴=,
故答案为:.
12.解:如图,连接BF交y轴于P,
∵四边形ABCD和四边形EFGO是矩形,点B,F的坐标分别为(﹣4,4),(2,1),
∴点C的坐标为(0,4),点G的坐标为(0,1),
∴CG=3,
∵BC∥GF,
∴==,
∴GP=1,PC=2,
∴点P的坐标为(0,2),
故答案为:(0,2).
13.解:∵两个相似三角形的最短边分别是5cm和3cm,
∴两个三角形的相似比为5:3,
设大三角形的周长为5x,则小三角形的周长为3x,
由题意得,5x﹣3x=12,
解得,x=6,
则5x=30,
故答案为:30.
14.解:∵四边形ABCD是矩形,
∴AB=CD=2,AD=BC=4,
∵四边形EFDC是矩形,
∴EF=CD=2,CE=DF,
∵余下的矩形EFDC∽矩形BCDA,
∴,
即=,
∴CE=1,
故答案为:1.
15.解:∵四边形ABCD是矩形,
∴AD⊥DC,
∴AC===,
∵按逆时针方向作矩形ABCD的相似矩形AB1C1C,
∴矩形AB1C1C的边长和矩形ABCD的边长的比为:2
∴矩形AB1C1C的面积和矩形ABCD的面积的比5:4,
∵矩形ABCD的面积=2×1=2,
∴矩形AB1C1C的面积=,
依此类推,矩形AB2C2C1的面积和矩形AB1C1C的面积的比5:4
∴矩形AB2C2C1的面积=
∴矩形AB3C3C2的面积=,
按此规律第4个矩形的面积为,
故答案为:.
16.解:如图所示:△ABC∽△DEF,
DE=,ED=2,EF=.
故答案为:,2,.
三.解答题(共8小题,满分56分)
17.证明:∵CD是斜边AB上的高.
∴∠ADC=∠CDB=90°,
又∵在Rt△ABC中,∠C=90°,
∴∠ACD+∠BCD=90°
∴∠A+∠ACD=90°,
∴∠A=∠BCD,
∴△ACD∽△CBD,
∴,
∴CD2=AD BD.
18.解:(1)△A1BC1如图所示,点C1的坐标(1,6).
(2)△A2B2C2如图所示,点C2的坐标(﹣6,4).
19.证明:(1)∵∠CED=∠CDA=90°,∠ECD=∠DCA,
∴△CED∽△CDA,
∴,即CD2=CE CA,
∵∠CFD=∠CDB=90°,∠FCD=∠DCB,
∴△CDF∽△CBD,
∴,即CD2=CB CF,
则CA CE=CB CF;
(2)∵∠CED=∠CFD=90°,
∴C,E,D,F四点共圆,
∴∠FED=∠FCD,∠DEC=∠DFC,
∴△COE∽△FOD,
20.证明:(1)∵∠EAC=∠DAB,
∴∠CAB=∠EAD,
∵∠ACB=∠AED=90°,
∴△ABC∽△ADE;
(2)由(1)知△ABC∽△ADE,
∴,
∵∠EAC=∠BAD,
∴△BAD∽△CAE;
(3)∵∠ACB=90°,BC=4,AC=3,
∴AB===5,
∵△ABC∽△ADE,
∴,
∴AD==,
如图,将△AED绕点A旋转,当点E落在线段CD上时,∠AEC=∠ADB=90°,
∴BD=.
21.(1)证明:∵四边形EFMN是正方形,
∴EF∥BC,
∴∠AEF=∠B,∠AFE=∠C,
∴△AEF∽△ABC.
(2)解:设正方形EFMN的边长为x.
∵△AEF∽△ABC,AD⊥BC,
∴=,
∴=,
∴x=8,
∴正方形的边长为8cm.
22.解:设宽度AB为x米,
∵DE∥BC,
∴△ABC∽△ADE,
∴=,
又∵BC=24,BD=12,DE=40,
∴=,
解得x=18,
答:河的宽度为18米.
23.(1)解:设EF=x,DF=2x,则DE=EF+DF=3x=AD
在Rt△ADF中,AD2+DF2=AF2,,
∵x>0,
∴x=1,
∴EF=1,DF=2,AD=3,
∴由三角形面积公式得:S△ADF==,
即;
(2)证明:
过D点作DK⊥DM交AC于点K,
∵∠1+∠KDF=90°,∠2+∠KDF=90°,
∴∠1=∠2,
∵∠3+∠4=90°,∠5+∠EFM=90°,
又∵∠4=∠EFM,
∴∠3=∠5,
在△ADK和△EDM中
,
∴△ADK≌△EDM(ASA),
∴DK=DM,AK=EM,
∴△MDK为等腰直角三角形,
∵DG⊥AC,
∴MK=2DG,
∴AM﹣EM=AM﹣AK=MK=2DG.
24.解:(1)△BME是等腰三角形,理由如下:
由题意可知EC=FC,CH⊥EF,
所以∠F=∠HEC.
∵FH∥BD,
∴∠F=∠MBF.
∴∠HEC=∠MBF.
又∠HEC=∠MEB,
∴∠MEB=∠MBE.
∴MB=ME.
∴△MBE是等腰三角形;
(2)①当∠DME=90°时,如图1,
∵MB=ME,
即∠MEB=∠MBE,
∴∠DBC=45°.
∴∠DBC=∠BDC,
∴BC=DC.
∴AB:BC=DC:BC=1;
②当∠DEM=90°时,如图2,过点M作MG⊥BC于G点,
∵∠MEB+∠DEC=90°,∠DEC+∠EDC=90°,
∠EDC=∠MEB=∠MBE.
由(1)得MB=ME,又MG⊥BC,
∴BE=2GE=2GB,
又BE=2EC,
∴EG=EC,则△MGE≌△HCE(ASA)
∴ME=HE.
又DE⊥MH,
∴∠MDE=∠EDC.
∴∠DBE=∠EDC=∠BDE=30°.
∴AB:BC=DC:BC=tan∠DBC=tan30°=.
综上所述AB:BC=1或.
一.选择题(共10小题,满分40分)
1.已知,则等于( )
A. B. C.2 D.3
2.如图,用图中的数据不能组成的比例是( )
A.2:4=1.5:3 B.3:1.5=4:2 C.2:3=1.5:4 D.1.5:2=3:4
3.点P是长度为1的线段上的黄金分割点,则较短线段的长度为( )
A. B. C. D.
4.将一个四边形放在2倍的放大镜下,则下列说法不正确的是( )
A.四边形的边长扩大为原来的2倍
B.四边形的各角扩大为原来的2倍
C.四边形的周长扩大为原来的2倍
D.四边形的面积扩大为原来的4倍
5.如图,在△ABC中,AD∥BC,点E在AB边上,EF∥BC,交AC边于点F,DE交AC边于点G,则下列结论中错误的是( )
A. B. C. D.
6.已知点P是线段AB的黄金分割点,AP>BP.记以AP为一边的正方形面积为S1,以BP、AB为邻边矩形的面积为S2,则( )
A.S1>S2 B.S1=S2
C.S1<S2 D.S1、S2大小不能确定
7.如图,AD是△ABC的中线,点E在AD上,AD=4DE,连接BE并延长交AC于点F,则AF:FC的值是( )
A.3:2 B.4:3 C.2:1 D.2:3
8.如图,点D、E分别在△ABC的边AB、AC上,且AB=9,AC=6,AD=3,若使△ADE与△ABC相似,则AE的长为( )
A.2 B. C.2或 D.3或
9.如图是用卡钳测量容器内径的示意图,现量得卡钳上A,D两个端点之间的距离为10cm,==,则容器的内径是( )
A.5cm B.10cm C.15cm D.20cm
10.如图,在直角坐标系中,有一等腰直角三角形OBA,∠OAB=90°,直角边OA在x轴正半轴上,且OA=1,将Rt△OBA绕原点O顺时针旋转90°,同时扩大边长的1倍,得到等腰直角三角形OB1A1(即A1O=2AO).同理,将Rt△OB1A1顺时针旋转90°,同时扩大边长1倍,得到等腰直角三角形OB2A2……依此规律,得到等腰直角三角形OB2019A2019,则点B2019的坐标为( )
A.(﹣22019,22019) B.(22019,﹣22019) C.(﹣22018,22018) D.(22018,﹣22018)
二.填空题(共6小题,满分24分)
11.如图L4,L5被一组平行线L1,L2,L3所截,显然三条平行线不是等距的,若=,则为 .
12.如图,矩形EFGO的两边在坐标轴上,点O为平面直角坐标系的原点,以y轴上的某一点为位似中心,作位似图形ABCD,且点B,F的坐标分别为(﹣4,4),(2,1),则位似中心的坐标为 .
13.两个相似三角形的最短边长分别为5cm和3cm,它们的周长之差为12cm,那么较大三角形的周长为 cm.
14.如图,矩形ABCD中,AB=2,BC=4,剪去一个矩形ABEF后,余下的矩形EFDC∽矩形BCDA,则EC的长为 .
15.如图,在矩形ABCD中,AD=2,CD=1,连接AC,以对角线AC为边,按逆时针方向作矩形ABCD的相似矩形AB1C1C,再连接AC1,以对角线AC1为边作矩形AB1C1C的相似矩形AB2C2C1,…,按此规律继续下去,则矩形AB4C4C3的面积为 .
16.如图,△ABC的顶点在1×3的正方形网格的格点上,在图中画出一个与△ABC相似但不全等的△DEF(△DEF的顶点在格点上),则△DEF的三边长分别是 .
三.解答题(共8小题,满分56分)
17.已知如图,Rt△ABC中,∠C=90°,CD是斜边上的高,求证:CD2=AD BD.
18.如图,在平面直角坐标系中,△ABC三个顶点的坐标分别为A(﹣2,1),B(﹣1,4),C(﹣3,2)
(1)画出△ABC关于点B中心对称的△A1BC1,并直接写出点C1的坐标.
(2)以原点O为位似中心,位似比为2:1,在y轴的左侧画出△ABC放大后的△A2B2C2,并直接写出点C2的坐标.
19.如图,在△ABC中,CD⊥AB,DE⊥AC,DF⊥BC,垂足分别为D,E,F.
(1)求证:CE CA=CF CB;
(2)EF交CD于点O,求证:△COE∽△FOD;
20.如图,△ABC与△ADE中,∠ACB=∠AED=90°,连接BD、CE,∠EAC=∠DAB.
(1)求证:△ABC∽△ADE;
(2)求证:△BAD∽△CAE;
(3)已知BC=4,AC=3,AE=.将△AED绕点A旋转,当点E落在线段CD上时,求BD的长.
21.如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFMN的一边MN在边BC上,顶点E、F分别在AB、AC上,其中BC=24cm,高AD=12cm.
(1)求证:△AEF∽△ABC:
(2)求正方形EFMN的边长.
22.为了估计河的宽度,勘测人员在河的对岸选定一个目标点A,在近岸分别取点B、D、E、C,使点A、B、D在一条直线上,且AD⊥DE,点A、C、E也在一条直线上,且DE∥BC.经测量BC=24米,BD=12米,DE=40米,求河的宽度AB为多少米?
23.已知在平行四边形ABCD中,过点D作DE⊥BC于点E,且AD=DE.连接AC交DE于点F,作DG⊥AC于点G.
(1)如图1,若,AF=,求DG的长;
(2)如图2,作EM⊥AC于点M,连接DM,求证:AM﹣EM=2DG.
24.如图,矩形ABCD中,E是BC上一点,点F是点E关于点C的对称点,过点F作对角线BD的平行线,交DC的延长线于点H,连接HE并延长与矩形的边AB、对角线BD于点N、M.
(1)试判定△BME的形状,并说明理由.
(2)若BE=2EC,连接DE,当△MED为直角三角形时,求AB:BC的值.
参考答案
一.选择题(共10小题,满分40分)
1.解:∵,
∴y=2x,
∴==.
故选:A.
2.解:A、2:4=1:2=1.5:3,能组成比例,错误;
B、3:1.5=2:1=4:2,能组成比例,错误;
C、2:3≠1.5:4;不能组成比例,正确;
D、1.5:2=3:4,能组成比例,错误;
故选:C.
3.解:较短线段的长度=1﹣×1
=,
故选:C.
4.解:放大前后的多边形按照比例放大与缩小,因此它们是相似多边形,放大后的倍数就是相似比,
∴选项:A,C,D正确,
故选:B.
5.解:∵EF∥BC
∴,∴答案A正确;
根据合比性质,则有
即:,∴答案D正确;
又∵AD∥EF
∴,∴答案B正确;
而,∴答案C错误.
故选:C.
6.解:根据黄金分割的概念得:AP:AB=PB:AP,即AP2=PB AB,
则S1:S2=AP2:(PB AB)=1,即S1=S2.
故选:B.
7.解:过点D作DG∥AC,与BF交于点G.
∵AD=4DE,
∴AE=3DE,
∵AD是△ABC的中线,
∴,
∴,即AF=3DG
∴,即FC=2DG,
∴AF:FC=3DG:2DG=3:2.
故选:A.
8.解:①若∠AED对应∠B时,=,即=,
解得AE=;
②当∠ADE对应∠B时,=,即=,
解得AE=2.
故选:C.
9.解:如图,连接AD,BC,
∵,∠AOD=∠BOC,
∴△AOD∽△BOC,
∴==,
又AD=10cm,
∴BC=2AD=20cm.
故选:D.
10.解:∵△AOB是等腰直角三角形,OA=1,
∴AB=OA=1,
∴B(1,1),
将Rt△AOB绕原点O顺时针旋转90°得到等腰直角三角形A1OB1,且A1O=2AO,
再将Rt△A1OB1绕原点O顺时针旋转90°得到等腰直角三角形A2OB2,且A2O=2A1O…,依此规律,
∴每4次循环一周,B1(2,﹣2),B2(﹣4,﹣4),B3(﹣8,8),B4(16,16),
∵2019÷4=502…3,
∴点B2019与B3同在一个象限内,
∵﹣4=﹣22,8=23,16=24,
∴点B2019(﹣22019,22019).
故选:A.
二.填空题(共6小题,满分24分)
11.解:∵L1∥L2∥L3,
∴=,
∴=,
故答案为:.
12.解:如图,连接BF交y轴于P,
∵四边形ABCD和四边形EFGO是矩形,点B,F的坐标分别为(﹣4,4),(2,1),
∴点C的坐标为(0,4),点G的坐标为(0,1),
∴CG=3,
∵BC∥GF,
∴==,
∴GP=1,PC=2,
∴点P的坐标为(0,2),
故答案为:(0,2).
13.解:∵两个相似三角形的最短边分别是5cm和3cm,
∴两个三角形的相似比为5:3,
设大三角形的周长为5x,则小三角形的周长为3x,
由题意得,5x﹣3x=12,
解得,x=6,
则5x=30,
故答案为:30.
14.解:∵四边形ABCD是矩形,
∴AB=CD=2,AD=BC=4,
∵四边形EFDC是矩形,
∴EF=CD=2,CE=DF,
∵余下的矩形EFDC∽矩形BCDA,
∴,
即=,
∴CE=1,
故答案为:1.
15.解:∵四边形ABCD是矩形,
∴AD⊥DC,
∴AC===,
∵按逆时针方向作矩形ABCD的相似矩形AB1C1C,
∴矩形AB1C1C的边长和矩形ABCD的边长的比为:2
∴矩形AB1C1C的面积和矩形ABCD的面积的比5:4,
∵矩形ABCD的面积=2×1=2,
∴矩形AB1C1C的面积=,
依此类推,矩形AB2C2C1的面积和矩形AB1C1C的面积的比5:4
∴矩形AB2C2C1的面积=
∴矩形AB3C3C2的面积=,
按此规律第4个矩形的面积为,
故答案为:.
16.解:如图所示:△ABC∽△DEF,
DE=,ED=2,EF=.
故答案为:,2,.
三.解答题(共8小题,满分56分)
17.证明:∵CD是斜边AB上的高.
∴∠ADC=∠CDB=90°,
又∵在Rt△ABC中,∠C=90°,
∴∠ACD+∠BCD=90°
∴∠A+∠ACD=90°,
∴∠A=∠BCD,
∴△ACD∽△CBD,
∴,
∴CD2=AD BD.
18.解:(1)△A1BC1如图所示,点C1的坐标(1,6).
(2)△A2B2C2如图所示,点C2的坐标(﹣6,4).
19.证明:(1)∵∠CED=∠CDA=90°,∠ECD=∠DCA,
∴△CED∽△CDA,
∴,即CD2=CE CA,
∵∠CFD=∠CDB=90°,∠FCD=∠DCB,
∴△CDF∽△CBD,
∴,即CD2=CB CF,
则CA CE=CB CF;
(2)∵∠CED=∠CFD=90°,
∴C,E,D,F四点共圆,
∴∠FED=∠FCD,∠DEC=∠DFC,
∴△COE∽△FOD,
20.证明:(1)∵∠EAC=∠DAB,
∴∠CAB=∠EAD,
∵∠ACB=∠AED=90°,
∴△ABC∽△ADE;
(2)由(1)知△ABC∽△ADE,
∴,
∵∠EAC=∠BAD,
∴△BAD∽△CAE;
(3)∵∠ACB=90°,BC=4,AC=3,
∴AB===5,
∵△ABC∽△ADE,
∴,
∴AD==,
如图,将△AED绕点A旋转,当点E落在线段CD上时,∠AEC=∠ADB=90°,
∴BD=.
21.(1)证明:∵四边形EFMN是正方形,
∴EF∥BC,
∴∠AEF=∠B,∠AFE=∠C,
∴△AEF∽△ABC.
(2)解:设正方形EFMN的边长为x.
∵△AEF∽△ABC,AD⊥BC,
∴=,
∴=,
∴x=8,
∴正方形的边长为8cm.
22.解:设宽度AB为x米,
∵DE∥BC,
∴△ABC∽△ADE,
∴=,
又∵BC=24,BD=12,DE=40,
∴=,
解得x=18,
答:河的宽度为18米.
23.(1)解:设EF=x,DF=2x,则DE=EF+DF=3x=AD
在Rt△ADF中,AD2+DF2=AF2,,
∵x>0,
∴x=1,
∴EF=1,DF=2,AD=3,
∴由三角形面积公式得:S△ADF==,
即;
(2)证明:
过D点作DK⊥DM交AC于点K,
∵∠1+∠KDF=90°,∠2+∠KDF=90°,
∴∠1=∠2,
∵∠3+∠4=90°,∠5+∠EFM=90°,
又∵∠4=∠EFM,
∴∠3=∠5,
在△ADK和△EDM中
,
∴△ADK≌△EDM(ASA),
∴DK=DM,AK=EM,
∴△MDK为等腰直角三角形,
∵DG⊥AC,
∴MK=2DG,
∴AM﹣EM=AM﹣AK=MK=2DG.
24.解:(1)△BME是等腰三角形,理由如下:
由题意可知EC=FC,CH⊥EF,
所以∠F=∠HEC.
∵FH∥BD,
∴∠F=∠MBF.
∴∠HEC=∠MBF.
又∠HEC=∠MEB,
∴∠MEB=∠MBE.
∴MB=ME.
∴△MBE是等腰三角形;
(2)①当∠DME=90°时,如图1,
∵MB=ME,
即∠MEB=∠MBE,
∴∠DBC=45°.
∴∠DBC=∠BDC,
∴BC=DC.
∴AB:BC=DC:BC=1;
②当∠DEM=90°时,如图2,过点M作MG⊥BC于G点,
∵∠MEB+∠DEC=90°,∠DEC+∠EDC=90°,
∠EDC=∠MEB=∠MBE.
由(1)得MB=ME,又MG⊥BC,
∴BE=2GE=2GB,
又BE=2EC,
∴EG=EC,则△MGE≌△HCE(ASA)
∴ME=HE.
又DE⊥MH,
∴∠MDE=∠EDC.
∴∠DBE=∠EDC=∠BDE=30°.
∴AB:BC=DC:BC=tan∠DBC=tan30°=.
综上所述AB:BC=1或.
