圆与圆的位置关系

(共22张PPT)
圆与圆的位置关系
　　 孙美荣
教学目标
（一）教学知识点
１、掌握圆与圆之间的几种位置关系
２、会根据两圆半径和圆心距的关系判断两圆的位置关系
（二）能力训练要求
１、经历探索两圆之间位置关系的过程，训练学生动探索能力
２、培养学生的视图能力和动手操作能力
（三）情感与价值观要求
通过探索圆与圆的位置关系，感受数学的严谨以及数学结论的确定性
O1
O2
O1
猜想：圆与圆之间会有哪几种位置关系？
观察：在两圆相对运动过程中，两圆公共点个数有怎样的变化？
在两圆相对运动过程中，两圆的公共点的个数
有0个、1个、3个三种情况
前面是半径不相等的两圆的位置关系,如果是半径相等的两圆呢
外离
外切
相交
重合
思考
如果两圆的半径分别为R、r（ R大于r ）,圆心距为d，你能说出两圆在不同位置关系时的R、r、ｄ三者的数量关系吗？　　
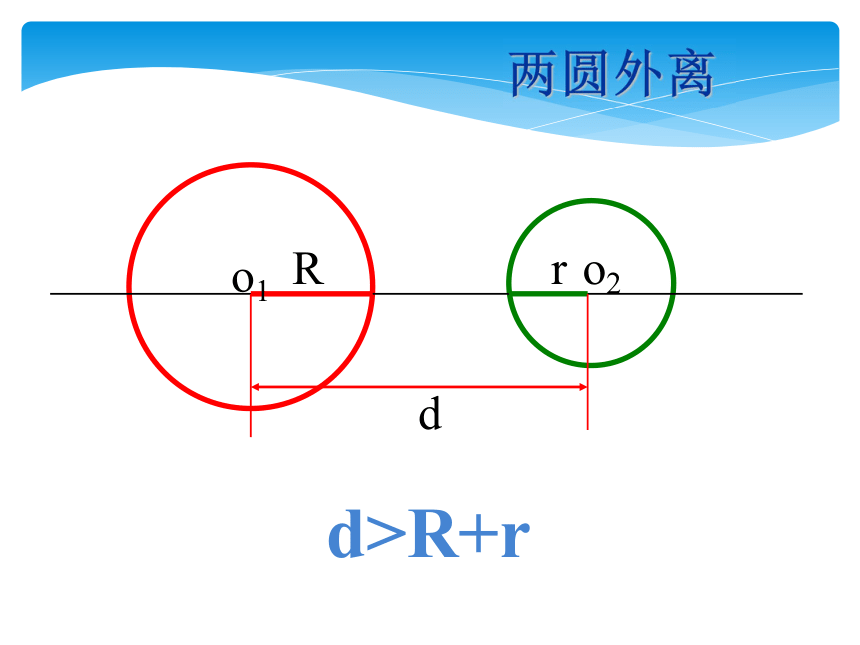
o1
o2
R
r
d
d>R+r
两圆外离
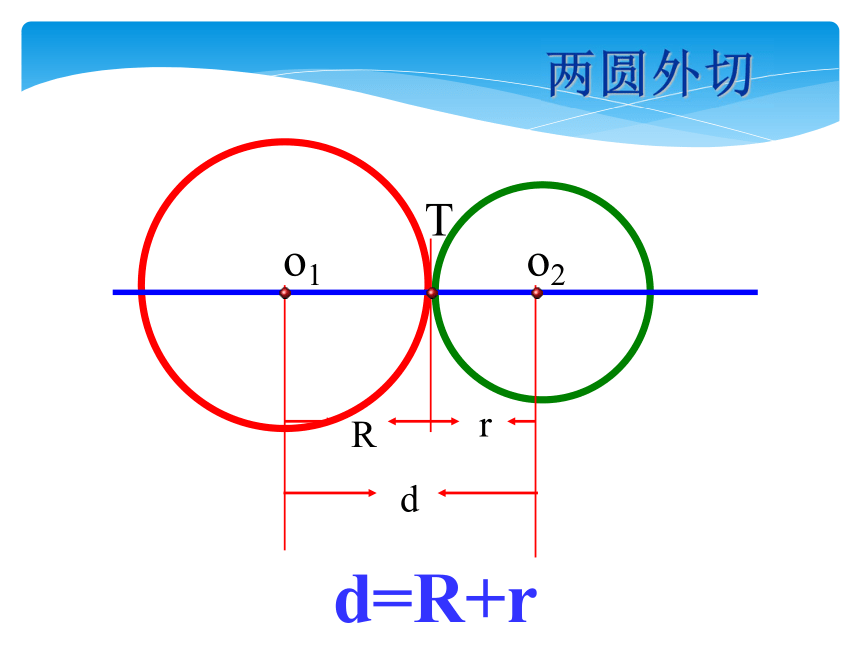
两圆外切
R
r
d
o1
o2
d=R+r
T
o1
o2
d
R
r
R-rr)
两圆相交
o1
o2
r
R
d
d=R-r (R>r)
T
两圆内切
O
O1
O2
R
r
d
0≤dr)
两圆内含
两圆外离
＞
.
.
两圆外切
两圆相交
两圆内切
两圆内含
＝
＜
＝
＜
＜
.
.
.
.
.
.
.
.
0≤
练习1
⊙O1和⊙O2的半径分别为3cm和4cm,如果O1O2
满足下列条件, ⊙O1和⊙O2各有什么位置关系
(1)O1O2=8cm( ); (2) O1O2=7cm ( );
(3) O1O2=5cm( ); (4) O1O2=1cm ( );
(5) O1O2=0.5cm( ); (6) O1和O2重合( );
外离
外切
相交
内切
内含
内含
两圆同心
例２
已知⊙Ａ、 ⊙Ｂ相切，圆心距为10cm，其中⊙Ａ的半径为4cm，求⊙Ｂ的半径。
温馨提示：相切有两种情况
如果两圆外切……
如果两圆内切……
已知⊙
的半径为
(1) ⊙
⊙
外切,则 的半径为 .
⊙
·
·
(2) ⊙
⊙
内切,则 的半径为 .
⊙
(3) ⊙
⊙
相切,则 的半径为 .
⊙
·
·
·
·
·
·
练习2
这是一块铁板，上面有A、B、C三个点，经测量，AB=9cm,BC=13cm,CA=14cm,以各顶点为圆心的三个圆两两外切。求各圆的半径。
A
C
B
.
.
.
练习3
1.已知⊙O半径是2cm,画圆使它的半径为1cm,且与⊙O相切,这样的圆可以画( )
A.1个 B.2个 C.5个 D.无数个
D
2.如图,已知⊙O的半径为2cm,A为⊙O上一点,画一个半径为1cm的⊙O1,使⊙O1与⊙O相切于点A,想一想怎样画 这样的圆能画多少个
.
.
O
A
拓展探究
注意：相切有两种情况
3、 已知，两圆相外切，半径分别是1㎝和2㎝ ，要作和这两个已知圆都相切且半径等于3㎝的圆，可作_____个。
4、 已知，两圆相离，半径分别是1㎝和2㎝ ，要作和这两个已知圆都相切且半径等于4㎝的圆，可作_____个。
5
6
注意：所作圆的半径大小，影响所作圆的个数。
你能找到规律吗？
两圆的位置关系
相切
相交
相离
外离
内含
外切
内切
相交
0≤dd=R-r
R-r d=R+r
d>R+r
作业:
课本:P55
习题28.2
第8，9题