2021-2022学年冀教版九年级数学上册25.3相似三角形 同步达标测评 (word版含解析)
文档属性
| 名称 | 2021-2022学年冀教版九年级数学上册25.3相似三角形 同步达标测评 (word版含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 363.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-29 00:00:00 | ||
图片预览




文档简介
2021-2022学年人教版九年级数学下册《27.2相似三角形》同步达标测评(附答案)
一.选择题(共15小题,满分45分)
1.已知△ABC与△DEF相似,又∠A=40°,∠B=60°,那么∠D不可能是( )
A.40° B.60° C.80° D.100°
2.如图△ABC∽△ACD,则下列式子中不成立的是( )
A.= B.= C.AC2=AD AB D.=
3.如果两个相似三角形的对应边之比为3:7,其中一个三角形的一边上的中线长为2,则另一个三角形对应中线的长为( )
A. B. C.或 D.无法确定
4.如图,在等边三角形ABC中,点D,E分别在AB,AC边上,如果△ADE∽△ABC,AD:AB=1:4,BC=8cm,那么△ADE的周长等于( )
A.2cm B.3cm C.6cm D.12cm
5.如图,已知在△ABC中,点D、点E是边BC上的两点,联结AD、AE,且AD=AE,如果△ABE∽△CBA,那么下列等式错误的是( )
A.AB2=BE BC B.CD AB=AD AC
C.AE2=CD BE D.AB AC=BE CD
6.下列结论中正确的是( )
A.有两条边长比值是3:4的两个直角三角形相似
B.一个角相等的两个等腰三角形相似
C.两边对应成比例且一个角对应相等的两个三角形相似
D.有一个角为60°的两个等腰三角形相似
7.下列说法中不正确的是( )
A.如果两个三角形全等,那么这两个三角形相似
B.如果两个三角形相似,且相似比为1,那么这两个三角形必全等
C.如果两个三角形都与另一个三角形相似,那么这两个三角形相似
D.如果两个三角形相似,那么它们一定能互相重合
8.如图,D是△ABC边AB延长线上一点,添加一个条件后,仍不能使△ACD∽△ABC的是( )
A.∠ACB=∠D B.∠ACD=∠ABC C. D.
9.如图△ABC中,点D、E分别在边AB、AC上,则在下列四个条件中:①∠AED=∠B;②DE∥BC;③;④AD BC=DE AC,能满足△ADE∽△ACB的条件有( )
A.1个 B.2个 C.3个 D.4个
10.如图,在四边形ABCD中,∠BAC=90°,AB=6,AC=8,E是BC的中点,AD∥BC,AE∥DC,EF⊥CD于点F.下列结论错误的是( )
A.四边形AECD的周长是20 B.△ABC∽△FEC
C.∠B+∠ACD=90° D.EF的长为
11.如图,F为 ABCD的边AD上一点,射线BF交CD的延长线于点E,则下列结论正确的是( )
A.= B.= C.= D.=
12.如图,AD∥CB,E、F分别在AB、CD上,且EF∥CB,若=,CD=15,则线段DF的长为( )
A.3 B.6 C.9 D.10
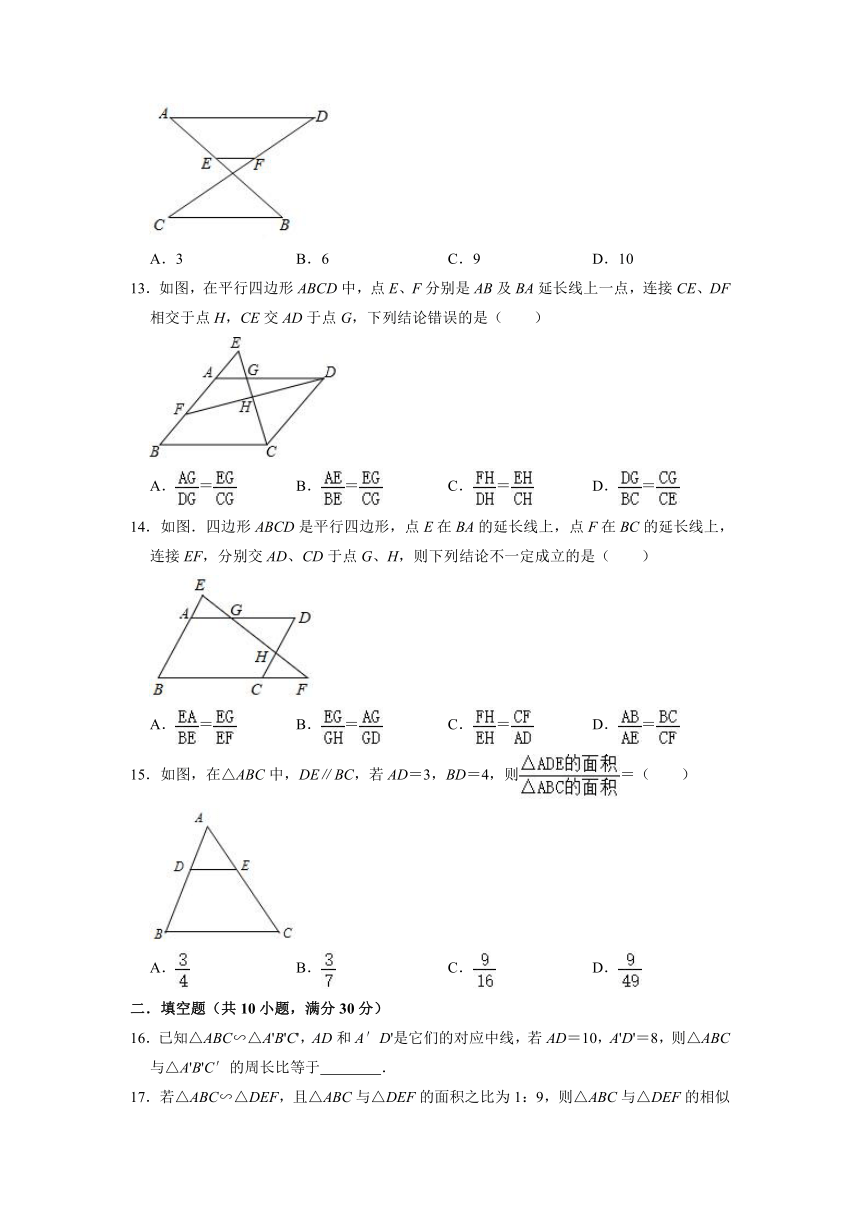
13.如图,在平行四边形ABCD中,点E、F分别是AB及BA延长线上一点,连接CE、DF相交于点H,CE交AD于点G,下列结论错误的是( )
A.= B.= C.= D.=
14.如图.四边形ABCD是平行四边形,点E在BA的延长线上,点F在BC的延长线上,连接EF,分别交AD、CD于点G、H,则下列结论不一定成立的是( )
A.= B.= C.= D.=
15.如图,在△ABC中,DE∥BC,若AD=3,BD=4,则=( )
A. B. C. D.
二.填空题(共10小题,满分30分)
16.已知△ABC∽△A'B'C',AD和A′D'是它们的对应中线,若AD=10,A'D'=8,则△ABC与△A'B'C′的周长比等于 .
17.若△ABC∽△DEF,且△ABC与△DEF的面积之比为1:9,则△ABC与△DEF的相似比为 .
18.已知△ABC∽△A'B'C',顶点A、B、C分别与顶点A'、B'、C'对应,AD、A'D'分别是BC、B'C'边上的中线,如果BC=3,AD=2.4,B'C'=2,那么A'D'的长是 .
19.如果两个相似三角形的周长之比为1:4.那么这两个三角形对应边上的高之比为 .
20.如图所示,在△ABC中D为AC边上一点,请你添加一个条件,使△ABC和△BCD相似,你所添加的条件是 .
21.如图,已知BD⊥AB于点B,AC⊥AB于点A,且BD=4,AC=3,AB=a,在线段AB上找一点E,使△BDE与△ACE相似,若这样的点E有且只有两个,则a的值是 .
22.如图,要使△ABC与△DBA相似,则只需添加一个适当的条件是 (填一个即可)
23.如图1,等边△ABC的顶点A在直角△MON的斜边MN上,顶点B与O重合,C在OM上.如图2,从O点出发在线段OM上平移等边△ABC,在开始平移△ABC同时,点P从△ABC的顶点B出发,沿线段BA运动,当点P运动到A时即停止运动,△ABC也随之停止平移.边AB,AC分别与线段MN交于点E,F,已知∠M=30°,∠MON=90°,OM=6,点P的移动速度是△ABC移动速度的2倍.当△PEF∽△NOM时,则线段OB的长为 .
24.如图,在 ABCD中,点E在边AD上,AE:AD=2:3,BE与AC交于点F.若AC=20,则AF的长为 .
25.如图,AB∥CD,AD、BC相交于点E过E作EF∥CD交BD于点F,如果AB=3,CD=6,那么EF的长是 .
三.解答题(共5小题,满分45分)
26.已知:如图,Rt△ABC∽Rt△ACD,若AC=3,BC=4,求AD.
27.两个相似三角形对应边的比是2:3.它们的面积和为65平方厘米,求较小三角形的面积.
28.如图,将△ABC绕点A旋转得到△ADE,连接BD,CE.
求证:△ADB∽△AEC.
29.已知,如图,△ABC中,AB=4,BC=8,D为BC边上一点,BD=2.求证:△ABD∽△CBA.
30.已知,在 ABCD中,∠ABC=45°,,点G是直线BC上一点,
(1)如图,若AD=6,连接BD,AG,且AG⊥BD于点E,
①求对角线BD的长;
②线段BG的长为 ;
(2)连接AG,作BF⊥AG,交直线AD于点F,当时,请直接写出线段BG的长.
参考答案
一.选择题(共15小题,满分45分)
1.解:∵△ABC∽△DEF,∠A=40°,∠B=60°,
∴∠A=∠D=40°或∠B=∠D=60°或∠C=∠D=180°﹣40°﹣60°=80°,
故选:D.
2.解:∵△ABC∽△ACD,
∴=,=,,
∴AC2=AD AB,
∴A、B、C成立,不符合题意;
D错误,符合题意,
故选:D.
3.解:∵相似三角形的对应边之比为3:7,
∴它们的对应中线的比为3:7,
∵其中一个三角形的一条中线为2,而这条中线可能是小三角形的,也可能是大三角形的,
∴另一个三角形对应的中线可能为,也可能是.
故选:C.
4.解:∵△ADE∽△ABC,AD:AB=1:4,
∴其周长比为1:4,
∵BC=8cm,三角形ABC为等边三角形,
∴△ABC的周长为24cm,
∴△ADE的周长为6cm.
故选:C.
5.解:∵△ABE∽△CBA,
∴AB:BC=BE:AB,
∴AB2=BE BC,所以A选项的结论正确;
∵△ABE∽△CBA,
∴∠BAE=∠C,∠AEB=∠BAC,
∵AD=AE,
∴∠ADE=∠AED,∠ACD=∠BCA,
∴∠ADE=∠BAC,
∵∠ADC=∠BAC,
∴△CAD∽△CBA,
∴CD:AC=AD:AB,
即CD AB=AD AC,所以B选项的结论正确;
∵△ABE∽△CBA,△CAD∽△CBA,
∴△CAD∽△ABE,
∴AD:BE=CD:AE,
即AD AE=CD BE,
∵AD=AE,
∴AE2=CD BE,所以C选项的结论正确;
∵△CBA∽△ABE,
∴AC:AE=CB:AB,
∴AB AC=AE CB,
∵AE2=CD BE,AE≠CB,
∴AB AC≠BE CD,所以D选项的结论不正确.
故选:D.
6.解:A、错误.比如,一个直角三角形的直角边为3,4,另一个直角三角形的一条直角边为3,斜边为4,这两个直角三角形不相似;
B、错误.当这个角一个是等腰三角形的顶角,一个是等腰三角形的底角,两个等腰三角形不相似;
C、错误;边对应成比例且一个角对应相等的两个三角形不一定相似;
D、正确.两个等边三角形相似;
故选:D.
7.解:A、如果两个三角形全等,则相似比为1,那么这两个三角形相似,故本选项不符合题意.
B、如果两个三角形相似,且相似比为 1,那么这两个三角形全等,故本选项不符合题意.
C、如果两个三角形都与另一个三角形相似,那么这两个三角形相似,故本选项不符合题意.
D、如果两个三角形相似,它们不一定全等,则它们不一定能互相重合,故本选项符合题意.
故选:D.
8.解:A、当∠ACB=∠D时,再由∠A=∠A,可得出△ACD∽△ABC,故此选项不合题意;
B、当∠ACD=∠ABC时,再由∠A=∠A,可得出△ACD∽△ABC,故此选项不合题意;
C、当时,无法得出△ACD∽△ABC,故此选项符合题意;
D、当时,再由∠A=∠A,可得出△ACD∽△ABC,故此选项不合题意;
故选:C.
9.解:①∠B=∠AED,∠A=∠A,则可判断△ADE∽△ACB,故①符合题意;
②DE∥BC,则△ADE∽△ABC,故②不符合题意,
③,且夹角∠A=∠A,能确定△ADE∽△ACB,故③符合题意;
④由AD BC=DE AC可得=,此时不确定∠ADE=∠ACB,故不能确定△ADE∽△ACB,故④不符合题意,
故选:B.
10.解:∵∠BAC=90°,AB=6,AC=8,
∴BC==10,
∵AD∥BC,AE∥DC,
∴四边形AECD是平行四边形,
∵∠BAC=90°,E是BC的中点,
∴AE=CE=BC=5,
∴四边形AECD是菱形,
∴菱形AECD的周长是20,
故A选项正确,不符合题意;
∵四边形AECD是菱形,
∴∠ACB=∠ACD,
∵∠B+∠ACB=90°,
∴∠B+∠ACD=90°,
故C选项正确,不符合题意;
如图,过A作AH⊥BC于点H,
∵S△ABC=BC AH=AB AC,
∴AH==,
∵点E是BC的中点,BC=10,四边形AECD是菱形,
∴CD=CE=5,
∵S AECD=CE AH=CD EF,
∴EF=AH=.
故D选项正确,不符合题意;
在Rt△EFC中,EF=,EC=5,
∴FC==,
在Rt△CAB中,AB=6,AC=8,BC=10,
∵=,=,=,
∴△ABC与△FEC不相似,故B选项错误,符合题意.
故选:B.
11.解:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴△ABF∽△DEF,△EFD∽△EBC,
∴,,,故选项A、C、D错误;
∵△ABF∽△DEF,△EFD∽△EBC,
∴△ABF∽△CEB,
∴,故选项B正确;
故选:B.
12.解:∵AD∥CB,EF∥CB,
∴AD∥EF∥CB,
∴==,
∴=,
即=,
∴DF=CD=×15=6.
故选:B.
13.解:∵四边形ABCD是平行四边形,
∴AB∥DC,AD∥BC,AD=BC,
∴△AEG∽△BEC,△EFH∽△CDH,△AEG∽△DCG,
∴=,故A正确,不符合题意;
=,故B错误,符合题意;
=,故C正确,不符合题意;
∵=,
∴+=+,
∴=,
∵AD=BC,
∴=,
∴=,故D正确,不符合题意.
综上,只有B符合题意.
故选:B.
14.解:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,AD=BC,
∴△EAG∽△EBF,△EAG∽△HDG,
∴,,故选项A、B成立,
∵CH∥BA,
∴,
∴,故选项C正确,
∵AG∥AC,CH∥BA,
∴,,
而无法证明是否成立,故选项D不一定成立,
故选:D.
15.解:∵AD=3,BD=4,
∴,
∵DE∥BC,
∴△ADE∽△ABC,
∴===.
故选:D.
二.填空题(共10小题,满分45分)
16.解:∵△ABC∽△A'B'C',AD和A'D'是它们的对应中线,AD=10,A'D'=8,
∴ABC与△A'B'C'的周长比=AD:A′D′=10:8=5:4.
故答案为:5:4.
17.解:∵△ABC∽△DEF,△ABC与△DEF的面积之比为1:9,
∴△ABC与△DEF的相似比为1:3,
故答案为:1:3.
18.解:∵△ABC∽△A'B'C',AD和A'D'是它们的对应中线,BC=3,AD=2.4,B'C'=2,
∴BC:B′C′=AD:A′D′,
∴2.4:A′D′=3:2,
∴A'D'的长是1.6,
故答案为:1.6.
19.解:∵两个相似三角形的周长之比为1:4,
∴这两个三角形的相似比为1:4,
∴两个相似三角形对应边上的高之比1:4;
故答案为:1:4.
20.解:∵∠C=∠BCD,
∴当∠A=∠CBD或∠CDB=∠ABC时,△ABC∽△BCD.
故答案是:∠A=∠CBD或∠CDB=∠ABC(答案不唯一).
21.解:∵BD⊥AB于点B,AC⊥AB,
∴∠A=∠B=90°,
当∠ACE=∠BDE时,△ACE∽△BDE,
∴,
∴AE=BE①,
当∠ACE=∠BED时,△ACE∽△BED,
∴,
即AE BE=AC BD=3×4=12②,
由①②可得:,
解得:BE=4,
∴AE=3,
∴AB=AE+BE=7,
即a=7,
当AE=3时,BE=4时,两个三角形相似,
当AE=4时,BE=3,两个三角形全等,
符合题目要求,
设AE=x,则BE=a﹣x,
∴x:4=3:(a﹣x),
整理得:x2﹣ax+12=0,
方程有唯一解时,△=a2﹣48=0,
解得:(舍去),
∴a=4,
当a=4时,AE:BE=3:4,两个三角形相似,
AE=BE=2时,两个三角形相似,
同样是两个点可以满足要求,
综上所述,△BDE与△ACE相似,若这样的点E有且仅有两个,
则a的值为7或4,
故答案为:7或4.
22.解:∵∠B=∠B(公共角),
∴可添加:∠C=∠BAD.
此时可利用两角法证明△ABC与△DBA相似.
故答案可为:∠C=∠BAD.
23.解:如图1中,设AB=AC=BC=a,
∵△ABC是等边三角形,
∴∠ACB=60°,
∵∠ACB=∠M+∠CAM,∠M=30°,
∴∠M=∠CAM=30°,
∴AC=CM=a,
∴OM=2a,即2a=6,
∴a=3,
如图2﹣1中,设OB=m,则PB=2m,
∵△PEF∽△NOM,
∴∠EPF=∠N=90°﹣30°=60°,
∴∠APF=∠ABC=60°,
∴PF∥BC,
∴∠AFP=∠ACP=60°,
∴△APF的等边三角形,
∵∠M+∠EBM=90°,
∴∠FEP=90°,
∴FE⊥AP,
∴AE=EP,
∴BM=6﹣m,
∴BE=BM=(6﹣m),
∴AE=EP=(6﹣m)﹣2m,
∵AP+PB=3,
∴6﹣m﹣4m+2m=3,
解得m=1,
∴OB=1,
当点P与A重合时,△PEF∽△NOM,
∵BP=2OB,
∴OB=,
综上所述,满足条件的OB的值为1或.
24.解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴△AEF∽△CBF,
∴,
∵AE:AD=2:3,
∴,
∴,
又∵AC=20,
∴AF=8,
故答案为:8.
25.解:∵AB∥CD,
∴△ABE∽△DCE,
∴==.
∵EF∥CD,
∴△BEF∽△BCD,
∴==,即=,
∴EF=2.
故答案为:2.
三.解答题(共5小题,满分45分)
26.解:∵AC=3,BC=4,∠ACB=90°,
由勾股定理得:AB=5,
∵Rt△ABC∽Rt△ACD,
∴,
即:,
解得:AD=,
∴AD的长为.
27.解:设两个三角形的面积分别为x,y,则有,
解得x=20,y=45
答:较小三角形面积为20.
28.证明:∵将△ABC绕点A旋转得到△ADE,
∴AC=AE,AB=AD,∠CAE=∠BAD,
∴,
∴△ADB∽△AEC.
29.证明:∵AB=4,BC=8,BD=2,
∴.
∵∠ABD=∠CBA,
∴△ABD∽△CBA.
30.解:(1)①如图1,过点D作DH⊥BC交BC延长线于H,
∴∠H=90°,
∵四边形ABCD是平行四边形,
∴BC=AD=6,CD=AB=3,CD∥AB,
∴∠DCH=∠ABC=45°,
在Rt△CHD中,CH=DH=CD=3,
∴BH=BC+CH=9,
在Rt△BHD中,BD===3;
②∵AG⊥BD,
∴∠AEB=∠AED=90°,
由①知,BD=3,
设BE=x,则DE=BD﹣BE=3﹣x,
在RtAEB中,AE2=AB2﹣BE2=(3)2﹣x2=18﹣x2,
在RtAED中,AE2=AD2﹣DE2=62﹣(3﹣x)2=﹣x2+6x﹣54,
∴18﹣x2=﹣x2+6x﹣54,
∴x=,
∴BE=,DE=3﹣=,
四边形ABCD是平行四边形,
∴AD∥BC,
∴△BEG∽△DEA,
∴,
∴,
∴BG=4,
故答案为:4;
(2)①当点F在点A左侧时,如图2,
过点A作AM⊥BC于M,过点B作BN⊥AD于N,
∴∠ANB=∠AMB=90°,
在Rt△ABM中,∠ABC=45°,AB=3,
∴BM=AM=AB=3,
∵AD∥BC,
∴∠MBN+∠ANB=180°,
∴∠MBN=90°,
∴∠FBN+∠MBH=90°,∠F+∠FBN=90°,
∴∠F=∠HBG,
∵∠HBG+∠H=∠GAM+∠AMB,
∴∠HBG+90°=∠GAM+90°,
∴∠HBG=∠GAM,
∴∠F=∠GAM,
∵∠BNF=∠GMA,
∴△BNF∽△GMA,
∴,
∴=,
∴GM=,
∴BG=BM﹣GM=3﹣=,
②当点F在点A右侧时,如图3,
同①的方法得,GM=,
∴BG=BM+GM=3+=,
即线段BG的长为或.
一.选择题(共15小题,满分45分)
1.已知△ABC与△DEF相似,又∠A=40°,∠B=60°,那么∠D不可能是( )
A.40° B.60° C.80° D.100°
2.如图△ABC∽△ACD,则下列式子中不成立的是( )
A.= B.= C.AC2=AD AB D.=
3.如果两个相似三角形的对应边之比为3:7,其中一个三角形的一边上的中线长为2,则另一个三角形对应中线的长为( )
A. B. C.或 D.无法确定
4.如图,在等边三角形ABC中,点D,E分别在AB,AC边上,如果△ADE∽△ABC,AD:AB=1:4,BC=8cm,那么△ADE的周长等于( )
A.2cm B.3cm C.6cm D.12cm
5.如图,已知在△ABC中,点D、点E是边BC上的两点,联结AD、AE,且AD=AE,如果△ABE∽△CBA,那么下列等式错误的是( )
A.AB2=BE BC B.CD AB=AD AC
C.AE2=CD BE D.AB AC=BE CD
6.下列结论中正确的是( )
A.有两条边长比值是3:4的两个直角三角形相似
B.一个角相等的两个等腰三角形相似
C.两边对应成比例且一个角对应相等的两个三角形相似
D.有一个角为60°的两个等腰三角形相似
7.下列说法中不正确的是( )
A.如果两个三角形全等,那么这两个三角形相似
B.如果两个三角形相似,且相似比为1,那么这两个三角形必全等
C.如果两个三角形都与另一个三角形相似,那么这两个三角形相似
D.如果两个三角形相似,那么它们一定能互相重合
8.如图,D是△ABC边AB延长线上一点,添加一个条件后,仍不能使△ACD∽△ABC的是( )
A.∠ACB=∠D B.∠ACD=∠ABC C. D.
9.如图△ABC中,点D、E分别在边AB、AC上,则在下列四个条件中:①∠AED=∠B;②DE∥BC;③;④AD BC=DE AC,能满足△ADE∽△ACB的条件有( )
A.1个 B.2个 C.3个 D.4个
10.如图,在四边形ABCD中,∠BAC=90°,AB=6,AC=8,E是BC的中点,AD∥BC,AE∥DC,EF⊥CD于点F.下列结论错误的是( )
A.四边形AECD的周长是20 B.△ABC∽△FEC
C.∠B+∠ACD=90° D.EF的长为
11.如图,F为 ABCD的边AD上一点,射线BF交CD的延长线于点E,则下列结论正确的是( )
A.= B.= C.= D.=
12.如图,AD∥CB,E、F分别在AB、CD上,且EF∥CB,若=,CD=15,则线段DF的长为( )
A.3 B.6 C.9 D.10
13.如图,在平行四边形ABCD中,点E、F分别是AB及BA延长线上一点,连接CE、DF相交于点H,CE交AD于点G,下列结论错误的是( )
A.= B.= C.= D.=
14.如图.四边形ABCD是平行四边形,点E在BA的延长线上,点F在BC的延长线上,连接EF,分别交AD、CD于点G、H,则下列结论不一定成立的是( )
A.= B.= C.= D.=
15.如图,在△ABC中,DE∥BC,若AD=3,BD=4,则=( )
A. B. C. D.
二.填空题(共10小题,满分30分)
16.已知△ABC∽△A'B'C',AD和A′D'是它们的对应中线,若AD=10,A'D'=8,则△ABC与△A'B'C′的周长比等于 .
17.若△ABC∽△DEF,且△ABC与△DEF的面积之比为1:9,则△ABC与△DEF的相似比为 .
18.已知△ABC∽△A'B'C',顶点A、B、C分别与顶点A'、B'、C'对应,AD、A'D'分别是BC、B'C'边上的中线,如果BC=3,AD=2.4,B'C'=2,那么A'D'的长是 .
19.如果两个相似三角形的周长之比为1:4.那么这两个三角形对应边上的高之比为 .
20.如图所示,在△ABC中D为AC边上一点,请你添加一个条件,使△ABC和△BCD相似,你所添加的条件是 .
21.如图,已知BD⊥AB于点B,AC⊥AB于点A,且BD=4,AC=3,AB=a,在线段AB上找一点E,使△BDE与△ACE相似,若这样的点E有且只有两个,则a的值是 .
22.如图,要使△ABC与△DBA相似,则只需添加一个适当的条件是 (填一个即可)
23.如图1,等边△ABC的顶点A在直角△MON的斜边MN上,顶点B与O重合,C在OM上.如图2,从O点出发在线段OM上平移等边△ABC,在开始平移△ABC同时,点P从△ABC的顶点B出发,沿线段BA运动,当点P运动到A时即停止运动,△ABC也随之停止平移.边AB,AC分别与线段MN交于点E,F,已知∠M=30°,∠MON=90°,OM=6,点P的移动速度是△ABC移动速度的2倍.当△PEF∽△NOM时,则线段OB的长为 .
24.如图,在 ABCD中,点E在边AD上,AE:AD=2:3,BE与AC交于点F.若AC=20,则AF的长为 .
25.如图,AB∥CD,AD、BC相交于点E过E作EF∥CD交BD于点F,如果AB=3,CD=6,那么EF的长是 .
三.解答题(共5小题,满分45分)
26.已知:如图,Rt△ABC∽Rt△ACD,若AC=3,BC=4,求AD.
27.两个相似三角形对应边的比是2:3.它们的面积和为65平方厘米,求较小三角形的面积.
28.如图,将△ABC绕点A旋转得到△ADE,连接BD,CE.
求证:△ADB∽△AEC.
29.已知,如图,△ABC中,AB=4,BC=8,D为BC边上一点,BD=2.求证:△ABD∽△CBA.
30.已知,在 ABCD中,∠ABC=45°,,点G是直线BC上一点,
(1)如图,若AD=6,连接BD,AG,且AG⊥BD于点E,
①求对角线BD的长;
②线段BG的长为 ;
(2)连接AG,作BF⊥AG,交直线AD于点F,当时,请直接写出线段BG的长.
参考答案
一.选择题(共15小题,满分45分)
1.解:∵△ABC∽△DEF,∠A=40°,∠B=60°,
∴∠A=∠D=40°或∠B=∠D=60°或∠C=∠D=180°﹣40°﹣60°=80°,
故选:D.
2.解:∵△ABC∽△ACD,
∴=,=,,
∴AC2=AD AB,
∴A、B、C成立,不符合题意;
D错误,符合题意,
故选:D.
3.解:∵相似三角形的对应边之比为3:7,
∴它们的对应中线的比为3:7,
∵其中一个三角形的一条中线为2,而这条中线可能是小三角形的,也可能是大三角形的,
∴另一个三角形对应的中线可能为,也可能是.
故选:C.
4.解:∵△ADE∽△ABC,AD:AB=1:4,
∴其周长比为1:4,
∵BC=8cm,三角形ABC为等边三角形,
∴△ABC的周长为24cm,
∴△ADE的周长为6cm.
故选:C.
5.解:∵△ABE∽△CBA,
∴AB:BC=BE:AB,
∴AB2=BE BC,所以A选项的结论正确;
∵△ABE∽△CBA,
∴∠BAE=∠C,∠AEB=∠BAC,
∵AD=AE,
∴∠ADE=∠AED,∠ACD=∠BCA,
∴∠ADE=∠BAC,
∵∠ADC=∠BAC,
∴△CAD∽△CBA,
∴CD:AC=AD:AB,
即CD AB=AD AC,所以B选项的结论正确;
∵△ABE∽△CBA,△CAD∽△CBA,
∴△CAD∽△ABE,
∴AD:BE=CD:AE,
即AD AE=CD BE,
∵AD=AE,
∴AE2=CD BE,所以C选项的结论正确;
∵△CBA∽△ABE,
∴AC:AE=CB:AB,
∴AB AC=AE CB,
∵AE2=CD BE,AE≠CB,
∴AB AC≠BE CD,所以D选项的结论不正确.
故选:D.
6.解:A、错误.比如,一个直角三角形的直角边为3,4,另一个直角三角形的一条直角边为3,斜边为4,这两个直角三角形不相似;
B、错误.当这个角一个是等腰三角形的顶角,一个是等腰三角形的底角,两个等腰三角形不相似;
C、错误;边对应成比例且一个角对应相等的两个三角形不一定相似;
D、正确.两个等边三角形相似;
故选:D.
7.解:A、如果两个三角形全等,则相似比为1,那么这两个三角形相似,故本选项不符合题意.
B、如果两个三角形相似,且相似比为 1,那么这两个三角形全等,故本选项不符合题意.
C、如果两个三角形都与另一个三角形相似,那么这两个三角形相似,故本选项不符合题意.
D、如果两个三角形相似,它们不一定全等,则它们不一定能互相重合,故本选项符合题意.
故选:D.
8.解:A、当∠ACB=∠D时,再由∠A=∠A,可得出△ACD∽△ABC,故此选项不合题意;
B、当∠ACD=∠ABC时,再由∠A=∠A,可得出△ACD∽△ABC,故此选项不合题意;
C、当时,无法得出△ACD∽△ABC,故此选项符合题意;
D、当时,再由∠A=∠A,可得出△ACD∽△ABC,故此选项不合题意;
故选:C.
9.解:①∠B=∠AED,∠A=∠A,则可判断△ADE∽△ACB,故①符合题意;
②DE∥BC,则△ADE∽△ABC,故②不符合题意,
③,且夹角∠A=∠A,能确定△ADE∽△ACB,故③符合题意;
④由AD BC=DE AC可得=,此时不确定∠ADE=∠ACB,故不能确定△ADE∽△ACB,故④不符合题意,
故选:B.
10.解:∵∠BAC=90°,AB=6,AC=8,
∴BC==10,
∵AD∥BC,AE∥DC,
∴四边形AECD是平行四边形,
∵∠BAC=90°,E是BC的中点,
∴AE=CE=BC=5,
∴四边形AECD是菱形,
∴菱形AECD的周长是20,
故A选项正确,不符合题意;
∵四边形AECD是菱形,
∴∠ACB=∠ACD,
∵∠B+∠ACB=90°,
∴∠B+∠ACD=90°,
故C选项正确,不符合题意;
如图,过A作AH⊥BC于点H,
∵S△ABC=BC AH=AB AC,
∴AH==,
∵点E是BC的中点,BC=10,四边形AECD是菱形,
∴CD=CE=5,
∵S AECD=CE AH=CD EF,
∴EF=AH=.
故D选项正确,不符合题意;
在Rt△EFC中,EF=,EC=5,
∴FC==,
在Rt△CAB中,AB=6,AC=8,BC=10,
∵=,=,=,
∴△ABC与△FEC不相似,故B选项错误,符合题意.
故选:B.
11.解:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴△ABF∽△DEF,△EFD∽△EBC,
∴,,,故选项A、C、D错误;
∵△ABF∽△DEF,△EFD∽△EBC,
∴△ABF∽△CEB,
∴,故选项B正确;
故选:B.
12.解:∵AD∥CB,EF∥CB,
∴AD∥EF∥CB,
∴==,
∴=,
即=,
∴DF=CD=×15=6.
故选:B.
13.解:∵四边形ABCD是平行四边形,
∴AB∥DC,AD∥BC,AD=BC,
∴△AEG∽△BEC,△EFH∽△CDH,△AEG∽△DCG,
∴=,故A正确,不符合题意;
=,故B错误,符合题意;
=,故C正确,不符合题意;
∵=,
∴+=+,
∴=,
∵AD=BC,
∴=,
∴=,故D正确,不符合题意.
综上,只有B符合题意.
故选:B.
14.解:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,AD=BC,
∴△EAG∽△EBF,△EAG∽△HDG,
∴,,故选项A、B成立,
∵CH∥BA,
∴,
∴,故选项C正确,
∵AG∥AC,CH∥BA,
∴,,
而无法证明是否成立,故选项D不一定成立,
故选:D.
15.解:∵AD=3,BD=4,
∴,
∵DE∥BC,
∴△ADE∽△ABC,
∴===.
故选:D.
二.填空题(共10小题,满分45分)
16.解:∵△ABC∽△A'B'C',AD和A'D'是它们的对应中线,AD=10,A'D'=8,
∴ABC与△A'B'C'的周长比=AD:A′D′=10:8=5:4.
故答案为:5:4.
17.解:∵△ABC∽△DEF,△ABC与△DEF的面积之比为1:9,
∴△ABC与△DEF的相似比为1:3,
故答案为:1:3.
18.解:∵△ABC∽△A'B'C',AD和A'D'是它们的对应中线,BC=3,AD=2.4,B'C'=2,
∴BC:B′C′=AD:A′D′,
∴2.4:A′D′=3:2,
∴A'D'的长是1.6,
故答案为:1.6.
19.解:∵两个相似三角形的周长之比为1:4,
∴这两个三角形的相似比为1:4,
∴两个相似三角形对应边上的高之比1:4;
故答案为:1:4.
20.解:∵∠C=∠BCD,
∴当∠A=∠CBD或∠CDB=∠ABC时,△ABC∽△BCD.
故答案是:∠A=∠CBD或∠CDB=∠ABC(答案不唯一).
21.解:∵BD⊥AB于点B,AC⊥AB,
∴∠A=∠B=90°,
当∠ACE=∠BDE时,△ACE∽△BDE,
∴,
∴AE=BE①,
当∠ACE=∠BED时,△ACE∽△BED,
∴,
即AE BE=AC BD=3×4=12②,
由①②可得:,
解得:BE=4,
∴AE=3,
∴AB=AE+BE=7,
即a=7,
当AE=3时,BE=4时,两个三角形相似,
当AE=4时,BE=3,两个三角形全等,
符合题目要求,
设AE=x,则BE=a﹣x,
∴x:4=3:(a﹣x),
整理得:x2﹣ax+12=0,
方程有唯一解时,△=a2﹣48=0,
解得:(舍去),
∴a=4,
当a=4时,AE:BE=3:4,两个三角形相似,
AE=BE=2时,两个三角形相似,
同样是两个点可以满足要求,
综上所述,△BDE与△ACE相似,若这样的点E有且仅有两个,
则a的值为7或4,
故答案为:7或4.
22.解:∵∠B=∠B(公共角),
∴可添加:∠C=∠BAD.
此时可利用两角法证明△ABC与△DBA相似.
故答案可为:∠C=∠BAD.
23.解:如图1中,设AB=AC=BC=a,
∵△ABC是等边三角形,
∴∠ACB=60°,
∵∠ACB=∠M+∠CAM,∠M=30°,
∴∠M=∠CAM=30°,
∴AC=CM=a,
∴OM=2a,即2a=6,
∴a=3,
如图2﹣1中,设OB=m,则PB=2m,
∵△PEF∽△NOM,
∴∠EPF=∠N=90°﹣30°=60°,
∴∠APF=∠ABC=60°,
∴PF∥BC,
∴∠AFP=∠ACP=60°,
∴△APF的等边三角形,
∵∠M+∠EBM=90°,
∴∠FEP=90°,
∴FE⊥AP,
∴AE=EP,
∴BM=6﹣m,
∴BE=BM=(6﹣m),
∴AE=EP=(6﹣m)﹣2m,
∵AP+PB=3,
∴6﹣m﹣4m+2m=3,
解得m=1,
∴OB=1,
当点P与A重合时,△PEF∽△NOM,
∵BP=2OB,
∴OB=,
综上所述,满足条件的OB的值为1或.
24.解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴△AEF∽△CBF,
∴,
∵AE:AD=2:3,
∴,
∴,
又∵AC=20,
∴AF=8,
故答案为:8.
25.解:∵AB∥CD,
∴△ABE∽△DCE,
∴==.
∵EF∥CD,
∴△BEF∽△BCD,
∴==,即=,
∴EF=2.
故答案为:2.
三.解答题(共5小题,满分45分)
26.解:∵AC=3,BC=4,∠ACB=90°,
由勾股定理得:AB=5,
∵Rt△ABC∽Rt△ACD,
∴,
即:,
解得:AD=,
∴AD的长为.
27.解:设两个三角形的面积分别为x,y,则有,
解得x=20,y=45
答:较小三角形面积为20.
28.证明:∵将△ABC绕点A旋转得到△ADE,
∴AC=AE,AB=AD,∠CAE=∠BAD,
∴,
∴△ADB∽△AEC.
29.证明:∵AB=4,BC=8,BD=2,
∴.
∵∠ABD=∠CBA,
∴△ABD∽△CBA.
30.解:(1)①如图1,过点D作DH⊥BC交BC延长线于H,
∴∠H=90°,
∵四边形ABCD是平行四边形,
∴BC=AD=6,CD=AB=3,CD∥AB,
∴∠DCH=∠ABC=45°,
在Rt△CHD中,CH=DH=CD=3,
∴BH=BC+CH=9,
在Rt△BHD中,BD===3;
②∵AG⊥BD,
∴∠AEB=∠AED=90°,
由①知,BD=3,
设BE=x,则DE=BD﹣BE=3﹣x,
在RtAEB中,AE2=AB2﹣BE2=(3)2﹣x2=18﹣x2,
在RtAED中,AE2=AD2﹣DE2=62﹣(3﹣x)2=﹣x2+6x﹣54,
∴18﹣x2=﹣x2+6x﹣54,
∴x=,
∴BE=,DE=3﹣=,
四边形ABCD是平行四边形,
∴AD∥BC,
∴△BEG∽△DEA,
∴,
∴,
∴BG=4,
故答案为:4;
(2)①当点F在点A左侧时,如图2,
过点A作AM⊥BC于M,过点B作BN⊥AD于N,
∴∠ANB=∠AMB=90°,
在Rt△ABM中,∠ABC=45°,AB=3,
∴BM=AM=AB=3,
∵AD∥BC,
∴∠MBN+∠ANB=180°,
∴∠MBN=90°,
∴∠FBN+∠MBH=90°,∠F+∠FBN=90°,
∴∠F=∠HBG,
∵∠HBG+∠H=∠GAM+∠AMB,
∴∠HBG+90°=∠GAM+90°,
∴∠HBG=∠GAM,
∴∠F=∠GAM,
∵∠BNF=∠GMA,
∴△BNF∽△GMA,
∴,
∴=,
∴GM=,
∴BG=BM﹣GM=3﹣=,
②当点F在点A右侧时,如图3,
同①的方法得,GM=,
∴BG=BM+GM=3+=,
即线段BG的长为或.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
