新疆农七师高级中学2012-2013学年高二第一次阶段性考试数学试题
文档属性
| 名称 | 新疆农七师高级中学2012-2013学年高二第一次阶段性考试数学试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 280.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-09 00:00:00 | ||
图片预览


文档简介
一、选择题:共12小题,每小题5分,共60分.在每小题的选项中,只有一项符合题目要求
1. 算法的三种基本结构是( )
A.顺序结构、模块结构、条件结构 B. 顺序结构、循环结构、模块结构
C. 顺序结构、条件结构、循环结构 D. 模块结构、条件结构、循环结构
2.以下给出对程序框图的几种说法:①任何一个程序框图都必须有起止框;②输人框只能放在开始框后,输出框只能放在结束框前;③判断框是唯一具有超过一个退出点的符号;④对于一个程序来说,判断框内的条件表述方法是唯一的.其中正确说法的个数是.( )
A.1 B.2 C.3 D.4
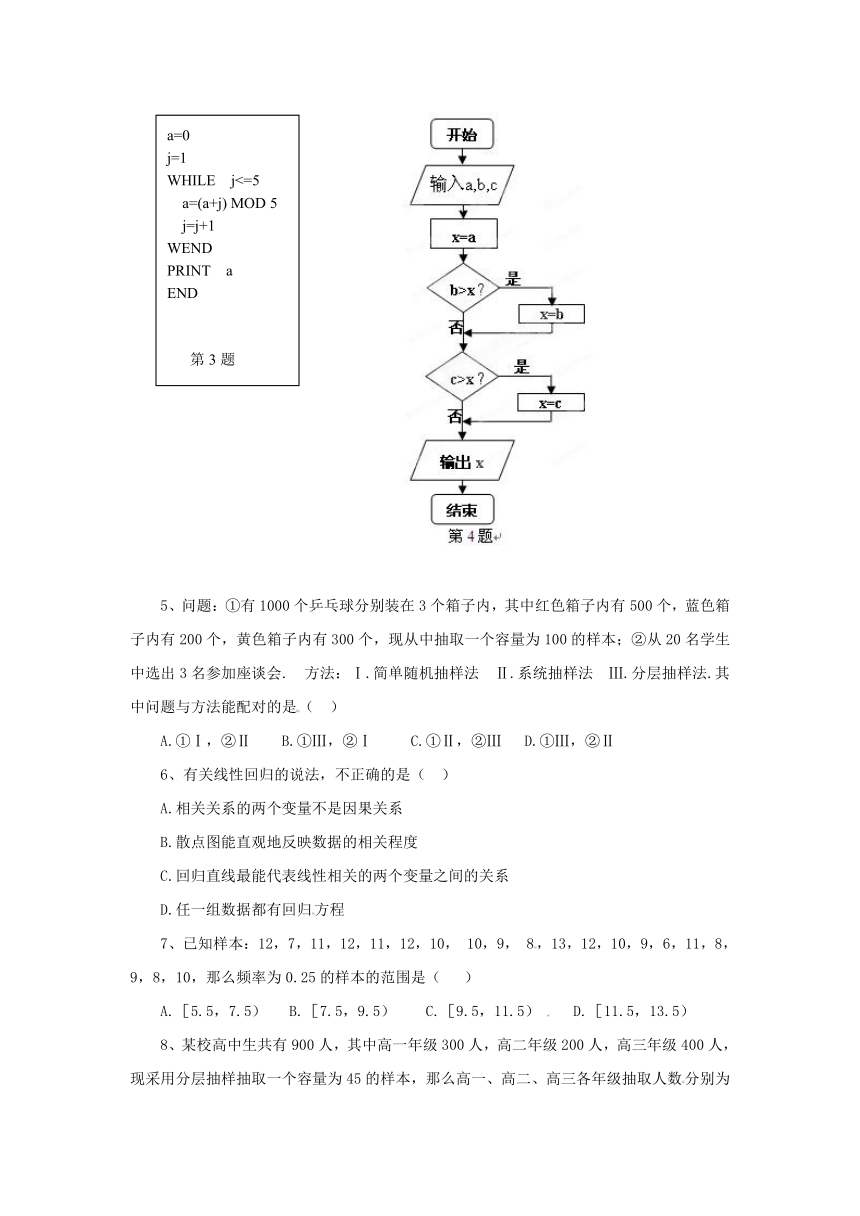
3.如下程序运行后输出的结果为 ( )
A. 50 B. 5 C. 25 D. 0
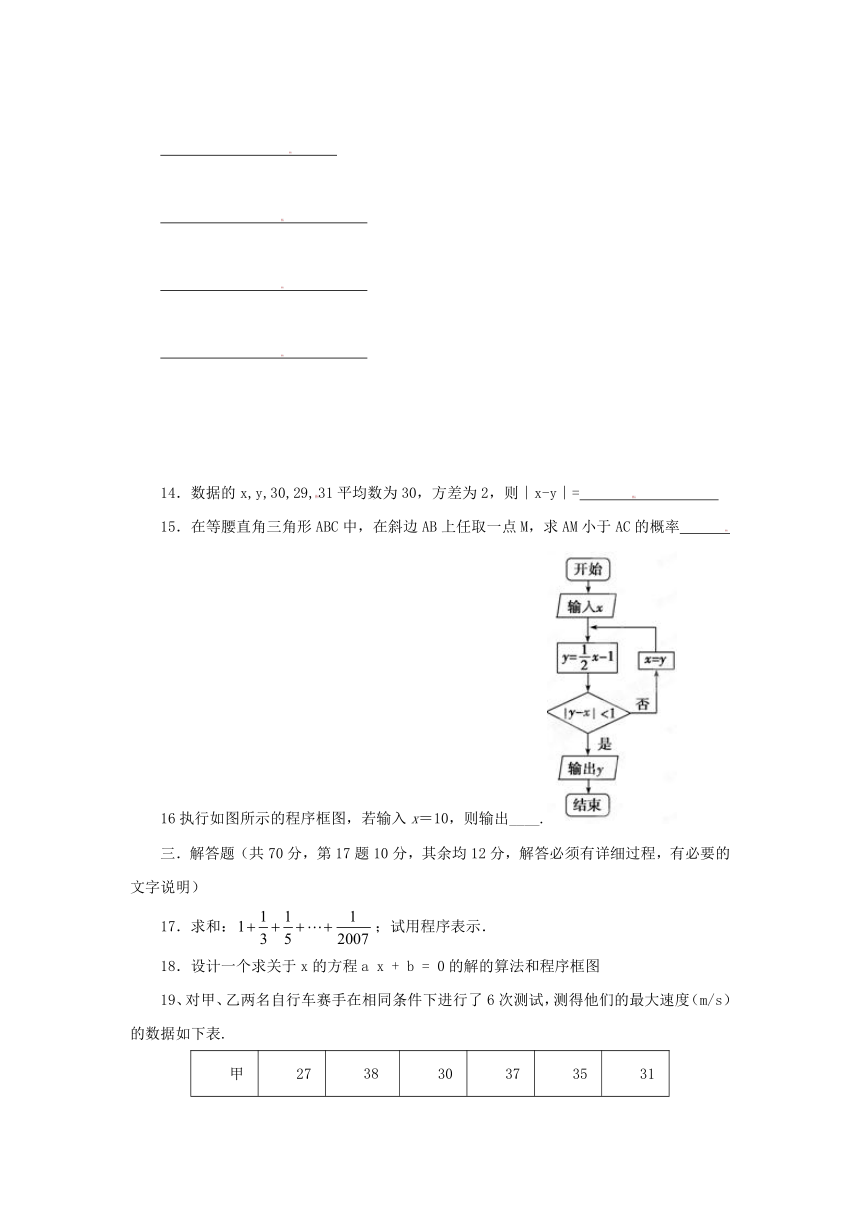
4.如下图所示的程序框图中,如果输入三个实数为a=3,b=7,c=2,则输出结果为( )
A.2 B.3 C.7 D.x
5、问题:①有1000个乒乓球分别装在3个箱子内,其中红色箱子内有500个,蓝色箱子内有200个,黄色箱子内有300个,现从中抽取一个容量为100的样本;②从20名学生中选出3名参加座谈会. 方法:Ⅰ.简单随机抽样法 Ⅱ.系统抽样法 Ⅲ.分层抽样法.其中问题与方法能配对的是( )
A.①Ⅰ,②Ⅱ B.①Ⅲ,②Ⅰ C.①Ⅱ,②Ⅲ D.①Ⅲ,②Ⅱ
6、有关线性回归的说法,不正确的是( )
A.相关关系的两个变量不是因果关系
B.散点图能直观地反映数据的相关程度
C.回归直线最能代表线性相关的两个变量之间的关系
D.任一组数据都有回归方程
7、已知样本:12,7,11,12,11,12,10, 10,9, 8,13,12,10,9,6,11,8,9,8,10,那么频率为0.25的样本的范围是( )
A.[5.5,7.5) B.[7.5,9.5) C.[9.5,11.5) D.[11.5,13.5)
8、某校高中生共有900人,其中高一年级300人,高二年级200人,高三年级400人,现采用分层抽样抽取一个容量为45的样本,那么高一、高二、高三各年级抽取人数分别为( )
A.15,5,25 B.15,15,15 C.10,5,30 D.15,10,20
9.某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
零件的个数x(个) 2 3 4 5
加工的时间y(小时) 2.5 3 4 4.5
则y关于x的线性回归方程为( )
(A)=x (B) =0.8x+2.05 (C)=0.7x+1.05 (D) =0.6x+0.95
注:=,=-,=x+
10.抛掷一个骰子,记A为事件“落地时向上的数是奇数”,B为事件“落地时向上的数是偶数”,C为事件“落地时向上的数是3的倍数”下面是是对立事件的是( ).
(A)、A与B (B)、A与C (C)、B与C (D)、A、B与C
11.若以连续掷两次骰子分别得到的点数m、 n作为P点的坐标,求点P落在圆外部的概率是 ( )
A. B. C. D.
12. 甲乙两艘轮船都要在某个泊位停靠6小时,假定他们在一昼夜的时间段中随机地到达,试求这两艘船中至少有一艘在停泊位时必须等待的概率( )
A B C D
二、填空题:本大题共4小题,每小题5分,共20分.把答案填在题中相应的横线上.
13写出一个求y=︱x-1︱的值的一个程序
14.数据的x,y,30,29,31平均数为30,方差为2,则∣x-y∣=
15.在等腰直角三角形ABC中,在斜边AB上任取一点M,求AM小于AC的概率
16执行如图所示的程序框图,若输入x=10,则输出____.
三.解答题(共70分,第17题10分,其余均12分,解答必须有详细过程,有必要的文字说明)
17.求和:;试用程序表示.
18.设计一个求关于x的方程a x + b = 0的解的算法和程序框图
19、对甲、乙两名自行车赛手在相同条件下进行了6次测试,测得他们的最大速度(m/s)的数据如下表.
甲 27 38 30 37 35 31
乙 33 29 38 34 28 36
(1)画出茎叶图,由茎叶图你能获得哪些信息?(2)分别求出甲、乙两名自行车赛手最大速度(m/s)数据的平均数、中位数、方差,并判断选谁参加比赛更合适.
20、有一个容量为100的样本,数据的分组及各组的频数如下:
(1)列出样本的频率分布表;(2)画出频率分布直方图和频率折线图;(3)由直方图确定样本的中位数。
21.已知盒中装有仅颜色不同的玻璃球6个,其中红球2个、黑球3个、白球1个.
(1)从中任取1个球, 求取得红球或黑球的概率;
(2)从中一次取2个不同的球,试列出所有基本事件;并求至少有一个是红球概率。
(3)从中取2次,每次取1个球,在放回的条件下求至少有一个是红球概率。
22.已知关于x的一元二次方程x-2(a-2)x-b+16=0.
(1)若a、b是一枚骰子先后投掷两次所得到的点数,求方程有两个正实数根的概率;
(2)若a∈[2,6],b∈[0,4],求一元二次方程没有实数根的概率
2012-2013学年第一学期高二年级第一阶段性考试
数学试卷答案:
一、选择题:
三、解答题:
17.求:;试用程序表示.
解
18.设计一个求关于x的方程a x + b = 0的解的算法和程序框图
解:算法
第一步,输入实数a,b.第二步,判断a是否为0,若是,执行第三步;否则,计算 ,并输出x,结束算法. 第三步,判断b是否为0.若是,则输出“方程的解为任意实数”;
分组 频数 频率
(2)设“一元二次方程无实数根”为事件B,则构成事件B的区域为B={(a,b)|2≤a≤6,0≤b≤4,(a-2)2+b2<16},其面积为S(B)=×π×42=4π,
故所求的概率为P(B)==.
a=0
j=1
WHILE j<=5
a=(a+j) MOD 5
j=j+1
WEND
PRINT a
END
第3题
S=0
i =1
DO
Loop UNTIL i >= 2009
Print S
END
1. 算法的三种基本结构是( )
A.顺序结构、模块结构、条件结构 B. 顺序结构、循环结构、模块结构
C. 顺序结构、条件结构、循环结构 D. 模块结构、条件结构、循环结构
2.以下给出对程序框图的几种说法:①任何一个程序框图都必须有起止框;②输人框只能放在开始框后,输出框只能放在结束框前;③判断框是唯一具有超过一个退出点的符号;④对于一个程序来说,判断框内的条件表述方法是唯一的.其中正确说法的个数是.( )
A.1 B.2 C.3 D.4
3.如下程序运行后输出的结果为 ( )
A. 50 B. 5 C. 25 D. 0
4.如下图所示的程序框图中,如果输入三个实数为a=3,b=7,c=2,则输出结果为( )
A.2 B.3 C.7 D.x
5、问题:①有1000个乒乓球分别装在3个箱子内,其中红色箱子内有500个,蓝色箱子内有200个,黄色箱子内有300个,现从中抽取一个容量为100的样本;②从20名学生中选出3名参加座谈会. 方法:Ⅰ.简单随机抽样法 Ⅱ.系统抽样法 Ⅲ.分层抽样法.其中问题与方法能配对的是( )
A.①Ⅰ,②Ⅱ B.①Ⅲ,②Ⅰ C.①Ⅱ,②Ⅲ D.①Ⅲ,②Ⅱ
6、有关线性回归的说法,不正确的是( )
A.相关关系的两个变量不是因果关系
B.散点图能直观地反映数据的相关程度
C.回归直线最能代表线性相关的两个变量之间的关系
D.任一组数据都有回归方程
7、已知样本:12,7,11,12,11,12,10, 10,9, 8,13,12,10,9,6,11,8,9,8,10,那么频率为0.25的样本的范围是( )
A.[5.5,7.5) B.[7.5,9.5) C.[9.5,11.5) D.[11.5,13.5)
8、某校高中生共有900人,其中高一年级300人,高二年级200人,高三年级400人,现采用分层抽样抽取一个容量为45的样本,那么高一、高二、高三各年级抽取人数分别为( )
A.15,5,25 B.15,15,15 C.10,5,30 D.15,10,20
9.某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
零件的个数x(个) 2 3 4 5
加工的时间y(小时) 2.5 3 4 4.5
则y关于x的线性回归方程为( )
(A)=x (B) =0.8x+2.05 (C)=0.7x+1.05 (D) =0.6x+0.95
注:=,=-,=x+
10.抛掷一个骰子,记A为事件“落地时向上的数是奇数”,B为事件“落地时向上的数是偶数”,C为事件“落地时向上的数是3的倍数”下面是是对立事件的是( ).
(A)、A与B (B)、A与C (C)、B与C (D)、A、B与C
11.若以连续掷两次骰子分别得到的点数m、 n作为P点的坐标,求点P落在圆外部的概率是 ( )
A. B. C. D.
12. 甲乙两艘轮船都要在某个泊位停靠6小时,假定他们在一昼夜的时间段中随机地到达,试求这两艘船中至少有一艘在停泊位时必须等待的概率( )
A B C D
二、填空题:本大题共4小题,每小题5分,共20分.把答案填在题中相应的横线上.
13写出一个求y=︱x-1︱的值的一个程序
14.数据的x,y,30,29,31平均数为30,方差为2,则∣x-y∣=
15.在等腰直角三角形ABC中,在斜边AB上任取一点M,求AM小于AC的概率
16执行如图所示的程序框图,若输入x=10,则输出____.
三.解答题(共70分,第17题10分,其余均12分,解答必须有详细过程,有必要的文字说明)
17.求和:;试用程序表示.
18.设计一个求关于x的方程a x + b = 0的解的算法和程序框图
19、对甲、乙两名自行车赛手在相同条件下进行了6次测试,测得他们的最大速度(m/s)的数据如下表.
甲 27 38 30 37 35 31
乙 33 29 38 34 28 36
(1)画出茎叶图,由茎叶图你能获得哪些信息?(2)分别求出甲、乙两名自行车赛手最大速度(m/s)数据的平均数、中位数、方差,并判断选谁参加比赛更合适.
20、有一个容量为100的样本,数据的分组及各组的频数如下:
(1)列出样本的频率分布表;(2)画出频率分布直方图和频率折线图;(3)由直方图确定样本的中位数。
21.已知盒中装有仅颜色不同的玻璃球6个,其中红球2个、黑球3个、白球1个.
(1)从中任取1个球, 求取得红球或黑球的概率;
(2)从中一次取2个不同的球,试列出所有基本事件;并求至少有一个是红球概率。
(3)从中取2次,每次取1个球,在放回的条件下求至少有一个是红球概率。
22.已知关于x的一元二次方程x-2(a-2)x-b+16=0.
(1)若a、b是一枚骰子先后投掷两次所得到的点数,求方程有两个正实数根的概率;
(2)若a∈[2,6],b∈[0,4],求一元二次方程没有实数根的概率
2012-2013学年第一学期高二年级第一阶段性考试
数学试卷答案:
一、选择题:
三、解答题:
17.求:;试用程序表示.
解
18.设计一个求关于x的方程a x + b = 0的解的算法和程序框图
解:算法
第一步,输入实数a,b.第二步,判断a是否为0,若是,执行第三步;否则,计算 ,并输出x,结束算法. 第三步,判断b是否为0.若是,则输出“方程的解为任意实数”;
分组 频数 频率
(2)设“一元二次方程无实数根”为事件B,则构成事件B的区域为B={(a,b)|2≤a≤6,0≤b≤4,(a-2)2+b2<16},其面积为S(B)=×π×42=4π,
故所求的概率为P(B)==.
a=0
j=1
WHILE j<=5
a=(a+j) MOD 5
j=j+1
WEND
PRINT a
END
第3题
S=0
i =1
DO
Loop UNTIL i >= 2009
Print S
END
同课章节目录
