2021-2022学年人教版九年级数学上册23.2.2 中心对称图形 同步练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版九年级数学上册23.2.2 中心对称图形 同步练习(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 493.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-29 13:56:39 | ||
图片预览


文档简介
2021——2022学年度人教版九年级数学上册 第二十三章 旋转 23.2.2 中心对称图形 同步练习
一、选择题
1.下列图形是中心对称图形的是( ).
A. B. C. D.
2.下列汽车标志中既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
3.如图所示的两个三角形(B、F、C、E四点共线)是中心对称图形,则对称中心是( )
A.点C B.点D C.线段BC的中点 D.线段FC的中点
4.在方格纸中,选择标有序号中的一个小正方形涂黑,与图中阴影部分构成中心对称图形,该小正方形的序号是( )
A. B. C. D.
5.在方格纸中,选择标有序号①②③④中的一个小正方形涂黑,与图中涂色部分构成中心对称图形.该小正方形的序号是( )
A.① B.② C.③ D.④
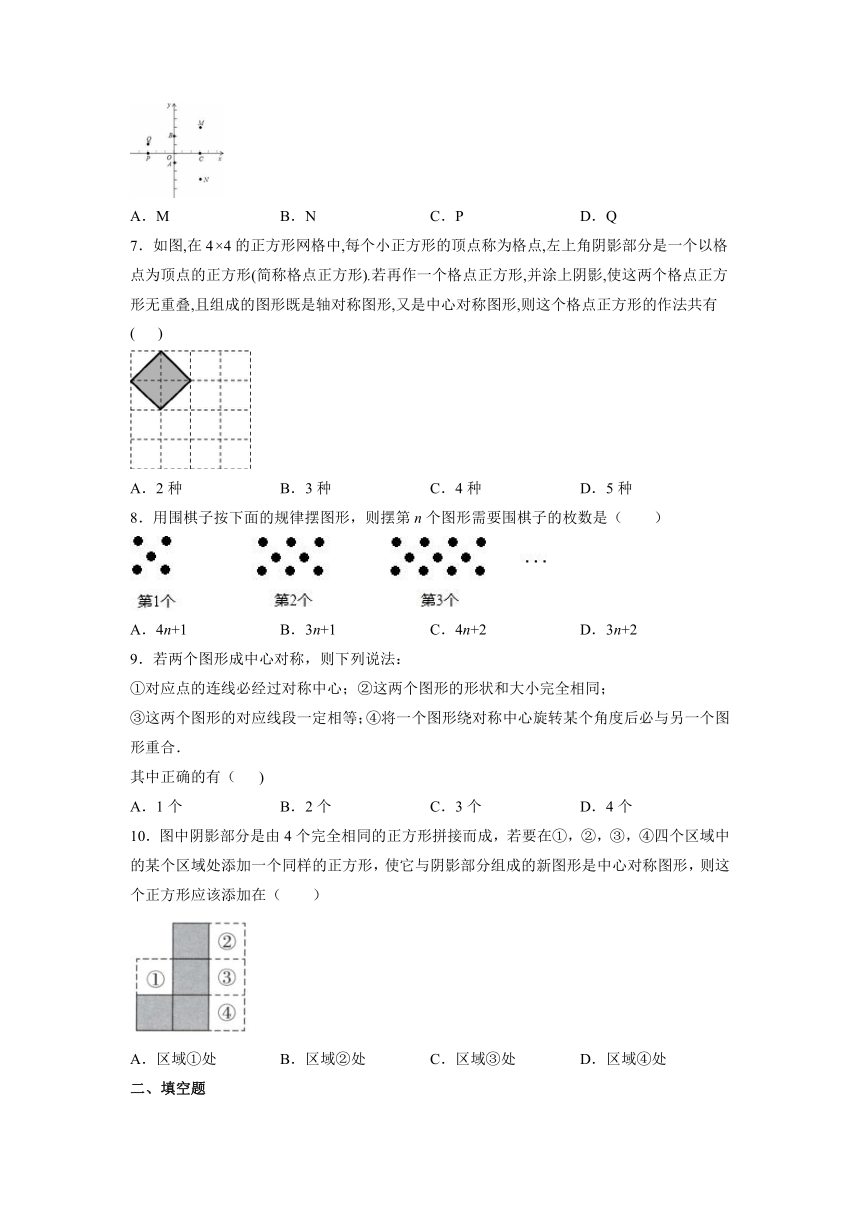
6.如图,点A,B,C的坐标分别为(0,﹣1),(0,2),(3,0).从下面四个点M(3,3),N(3,﹣3),P(﹣3,0),Q(﹣3,1)中选择一个点,以A,B,C与该点为顶点的四边形不是中心对称图形,则该点是( )
A.M B.N C.P D.Q
7.如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个格点正方形,并涂上阴影,使这两个格点正方形无重叠,且组成的图形既是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有 ( )
A.2种 B.3种 C.4种 D.5种
8.用围棋子按下面的规律摆图形,则摆第n个图形需要围棋子的枚数是( )
A.4n+1 B.3n+1 C.4n+2 D.3n+2
9.若两个图形成中心对称,则下列说法:
①对应点的连线必经过对称中心;②这两个图形的形状和大小完全相同;
③这两个图形的对应线段一定相等;④将一个图形绕对称中心旋转某个角度后必与另一个图形重合.
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
10.图中阴影部分是由4个完全相同的正方形拼接而成,若要在①,②,③,④四个区域中的某个区域处添加一个同样的正方形,使它与阴影部分组成的新图形是中心对称图形,则这个正方形应该添加在( )
A.区域①处 B.区域②处 C.区域③处 D.区域④处
二、填空题
11.等腰三角形、等边三角形、矩形、正方形和圆这五个图形中,既是轴对称图形又是中心对称图形的个数是__.
12.仔细观察艺术字田日,则在英文字母M,N,O,E,I,J中与其具有相同对称特征的是_____________.
13.在平面内,相交的两条直线是中心对称图形,它的对称中心是________.
14.方格纸中,若三角形的个顶点分别在小正方形的顶点(格点)上,这样的三角形叫格点三角形.在如图的方格纸中,画出与成中心对称的格点三角形________.
15.如图,平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1于点B2成中心对称,如此作下去,则△B2020A2021B2021的顶点A2021的坐标是___
三、解答题
16.在26个英文大写正体字母中,哪些字母是中心对称图形?
A B C D E F G H I J K L M
N O P Q R S T U V W X Y Z
17.如图1、图2都是由边长为1的小菱形构成的网格,每个小菱形的顶点称为格点.已知点A,B,C均在格点上,要求作一个多边形使这三个点在这个多边形的边(包括顶点)上,且多边形的顶点在网格的顶点上.
(1)在图1中作一个三角形是轴对称图形;
(2)在图2中作一个四边形既是轴对称图形又是中心对称图形.
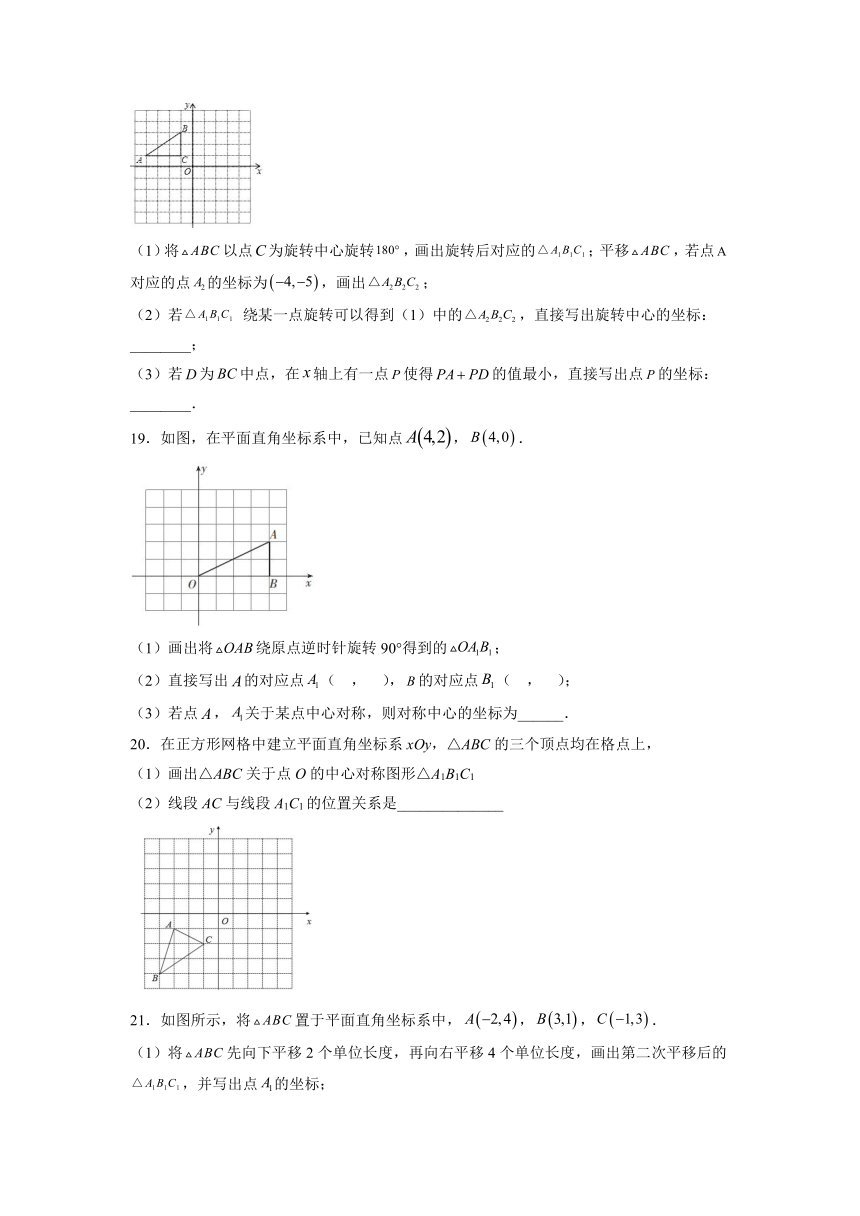
18.如图,在平面直角坐标系中,的三个顶点分别是,,.
(1)将以点为旋转中心旋转,画出旋转后对应的;平移,若点对应的点的坐标为,画出;
(2)若 绕某一点旋转可以得到(1)中的,直接写出旋转中心的坐标:________;
(3)若为中点,在轴上有一点使得的值最小,直接写出点的坐标:________.
19.如图,在平面直角坐标系中,已知点,.
(1)画出将绕原点逆时针旋转90°得到的;
(2)直接写出的对应点( , ),的对应点( , );
(3)若点,关于某点中心对称,则对称中心的坐标为______.
20.在正方形网格中建立平面直角坐标系xOy,△ABC的三个顶点均在格点上,
(1)画出△ABC关于点O的中心对称图形△A1B1C1
(2)线段AC与线段A1C1的位置关系是______________
21.如图所示,将置于平面直角坐标系中,,,.
(1)将先向下平移2个单位长度,再向右平移4个单位长度,画出第二次平移后的,并写出点的坐标;
(2)以点为对称中心,画出与成中心对称的,并写出点的坐标.
22.只用直尺(无刻度)完成下列作图:
(1)如图1,过正方形ABCD的顶点A作一条直线平分这个正方形的面积;
(2)如图2,不过正方形EFGH的顶点作直线l平分这个正方形的面积;
(3)如图3,五个边长相等的正方形组成了一个“L型”图形,作直线m平分这个“L型”图形的面积.
23.如图,正方形ABCD与正方形A1B1C1D1关于某点中心对称,已知A, D1 ,D三点的坐标分别是(0,4),(0,3),(0,2).
(1)对称中心的坐标;
(2)写出顶点B, C, B1 , C1的坐标.
【参考答案】
1.A 2.C 3.D 4.C 5.D 6.C 7.C 8.D 9.C 10.B
11.3
12.O,I
13.两条直线的交点
14.
15.
16.H,I,N,O,S,X,Z
17.(1)如图1所示;
(2)如图2所示.
18.解:如图所示,和,即为所求;
(2)如图,连接,交点即为旋转中心,
所以旋转中心坐标为:;
(3)为的中点,则
确定关于轴的对称点
连接交轴于 则P即为所求作的点,
19.(1)先根据旋转的性质画出点,再顺次连接点即可得,如图所示:
(2)绕原点逆时针旋转的点坐标变换规律:先将横、纵坐标互换位置,再将横坐标变为相反数,
,
,
故答案为:;
(3)由中心对称的定义得:点,的中心对称点为线段的中点,
则对称中心的坐标为,即,
故答案为:.
20.解:(1)如图所示,△即为所求.
(2)由中心对称的性质可知:线段AC与线段A1C1平行且相等,
线段AC与线段A1C1的位置关系是平行,
故答案是:平行.
21.解:(1)如图,△为所作;;
(2)如图,△为所作;.
22.(1)如图直线l如图所示.
(2)如图直线l如图所示.
(3)直线m如图所示.
23.(1)根据对称中心的性质,可得
对称中心的坐标是D1D的中点,
∵D1,D的坐标分别是(0,3),(0,2),
∴对称中心的坐标是(0,2.5).
(2)∵A,D的坐标分别是(0,4),(0,2),
∴正方形ABCD与正方形A1B1C1D1的边长都是:4﹣2=2,
∴B,C的坐标分别是(﹣2,4),(﹣2,2),
∵A1D1=2,D1的坐标是(0,3),
∴A1的坐标是(0,1),
∴B1,C1的坐标分别是(2,1),(2,3),
综上,可得顶点B,C,B1,C1的坐标分别是(﹣2,4),(﹣2,2),(2,1),(2,3).
一、选择题
1.下列图形是中心对称图形的是( ).
A. B. C. D.
2.下列汽车标志中既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
3.如图所示的两个三角形(B、F、C、E四点共线)是中心对称图形,则对称中心是( )
A.点C B.点D C.线段BC的中点 D.线段FC的中点
4.在方格纸中,选择标有序号中的一个小正方形涂黑,与图中阴影部分构成中心对称图形,该小正方形的序号是( )
A. B. C. D.
5.在方格纸中,选择标有序号①②③④中的一个小正方形涂黑,与图中涂色部分构成中心对称图形.该小正方形的序号是( )
A.① B.② C.③ D.④
6.如图,点A,B,C的坐标分别为(0,﹣1),(0,2),(3,0).从下面四个点M(3,3),N(3,﹣3),P(﹣3,0),Q(﹣3,1)中选择一个点,以A,B,C与该点为顶点的四边形不是中心对称图形,则该点是( )
A.M B.N C.P D.Q
7.如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个格点正方形,并涂上阴影,使这两个格点正方形无重叠,且组成的图形既是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有 ( )
A.2种 B.3种 C.4种 D.5种
8.用围棋子按下面的规律摆图形,则摆第n个图形需要围棋子的枚数是( )
A.4n+1 B.3n+1 C.4n+2 D.3n+2
9.若两个图形成中心对称,则下列说法:
①对应点的连线必经过对称中心;②这两个图形的形状和大小完全相同;
③这两个图形的对应线段一定相等;④将一个图形绕对称中心旋转某个角度后必与另一个图形重合.
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
10.图中阴影部分是由4个完全相同的正方形拼接而成,若要在①,②,③,④四个区域中的某个区域处添加一个同样的正方形,使它与阴影部分组成的新图形是中心对称图形,则这个正方形应该添加在( )
A.区域①处 B.区域②处 C.区域③处 D.区域④处
二、填空题
11.等腰三角形、等边三角形、矩形、正方形和圆这五个图形中,既是轴对称图形又是中心对称图形的个数是__.
12.仔细观察艺术字田日,则在英文字母M,N,O,E,I,J中与其具有相同对称特征的是_____________.
13.在平面内,相交的两条直线是中心对称图形,它的对称中心是________.
14.方格纸中,若三角形的个顶点分别在小正方形的顶点(格点)上,这样的三角形叫格点三角形.在如图的方格纸中,画出与成中心对称的格点三角形________.
15.如图,平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1于点B2成中心对称,如此作下去,则△B2020A2021B2021的顶点A2021的坐标是___
三、解答题
16.在26个英文大写正体字母中,哪些字母是中心对称图形?
A B C D E F G H I J K L M
N O P Q R S T U V W X Y Z
17.如图1、图2都是由边长为1的小菱形构成的网格,每个小菱形的顶点称为格点.已知点A,B,C均在格点上,要求作一个多边形使这三个点在这个多边形的边(包括顶点)上,且多边形的顶点在网格的顶点上.
(1)在图1中作一个三角形是轴对称图形;
(2)在图2中作一个四边形既是轴对称图形又是中心对称图形.
18.如图,在平面直角坐标系中,的三个顶点分别是,,.
(1)将以点为旋转中心旋转,画出旋转后对应的;平移,若点对应的点的坐标为,画出;
(2)若 绕某一点旋转可以得到(1)中的,直接写出旋转中心的坐标:________;
(3)若为中点,在轴上有一点使得的值最小,直接写出点的坐标:________.
19.如图,在平面直角坐标系中,已知点,.
(1)画出将绕原点逆时针旋转90°得到的;
(2)直接写出的对应点( , ),的对应点( , );
(3)若点,关于某点中心对称,则对称中心的坐标为______.
20.在正方形网格中建立平面直角坐标系xOy,△ABC的三个顶点均在格点上,
(1)画出△ABC关于点O的中心对称图形△A1B1C1
(2)线段AC与线段A1C1的位置关系是______________
21.如图所示,将置于平面直角坐标系中,,,.
(1)将先向下平移2个单位长度,再向右平移4个单位长度,画出第二次平移后的,并写出点的坐标;
(2)以点为对称中心,画出与成中心对称的,并写出点的坐标.
22.只用直尺(无刻度)完成下列作图:
(1)如图1,过正方形ABCD的顶点A作一条直线平分这个正方形的面积;
(2)如图2,不过正方形EFGH的顶点作直线l平分这个正方形的面积;
(3)如图3,五个边长相等的正方形组成了一个“L型”图形,作直线m平分这个“L型”图形的面积.
23.如图,正方形ABCD与正方形A1B1C1D1关于某点中心对称,已知A, D1 ,D三点的坐标分别是(0,4),(0,3),(0,2).
(1)对称中心的坐标;
(2)写出顶点B, C, B1 , C1的坐标.
【参考答案】
1.A 2.C 3.D 4.C 5.D 6.C 7.C 8.D 9.C 10.B
11.3
12.O,I
13.两条直线的交点
14.
15.
16.H,I,N,O,S,X,Z
17.(1)如图1所示;
(2)如图2所示.
18.解:如图所示,和,即为所求;
(2)如图,连接,交点即为旋转中心,
所以旋转中心坐标为:;
(3)为的中点,则
确定关于轴的对称点
连接交轴于 则P即为所求作的点,
19.(1)先根据旋转的性质画出点,再顺次连接点即可得,如图所示:
(2)绕原点逆时针旋转的点坐标变换规律:先将横、纵坐标互换位置,再将横坐标变为相反数,
,
,
故答案为:;
(3)由中心对称的定义得:点,的中心对称点为线段的中点,
则对称中心的坐标为,即,
故答案为:.
20.解:(1)如图所示,△即为所求.
(2)由中心对称的性质可知:线段AC与线段A1C1平行且相等,
线段AC与线段A1C1的位置关系是平行,
故答案是:平行.
21.解:(1)如图,△为所作;;
(2)如图,△为所作;.
22.(1)如图直线l如图所示.
(2)如图直线l如图所示.
(3)直线m如图所示.
23.(1)根据对称中心的性质,可得
对称中心的坐标是D1D的中点,
∵D1,D的坐标分别是(0,3),(0,2),
∴对称中心的坐标是(0,2.5).
(2)∵A,D的坐标分别是(0,4),(0,2),
∴正方形ABCD与正方形A1B1C1D1的边长都是:4﹣2=2,
∴B,C的坐标分别是(﹣2,4),(﹣2,2),
∵A1D1=2,D1的坐标是(0,3),
∴A1的坐标是(0,1),
∴B1,C1的坐标分别是(2,1),(2,3),
综上,可得顶点B,C,B1,C1的坐标分别是(﹣2,4),(﹣2,2),(2,1),(2,3).
同课章节目录
