3.2.2 函数模型的应用实例 课后作业(Word版,含答案)
文档属性
| 名称 | 3.2.2 函数模型的应用实例 课后作业(Word版,含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 207.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-30 08:25:35 | ||
图片预览


文档简介
3.2.2 函数模型的应用实例
时间:45分钟 分值:100分
一、选择题(每小题6分,共计36分)
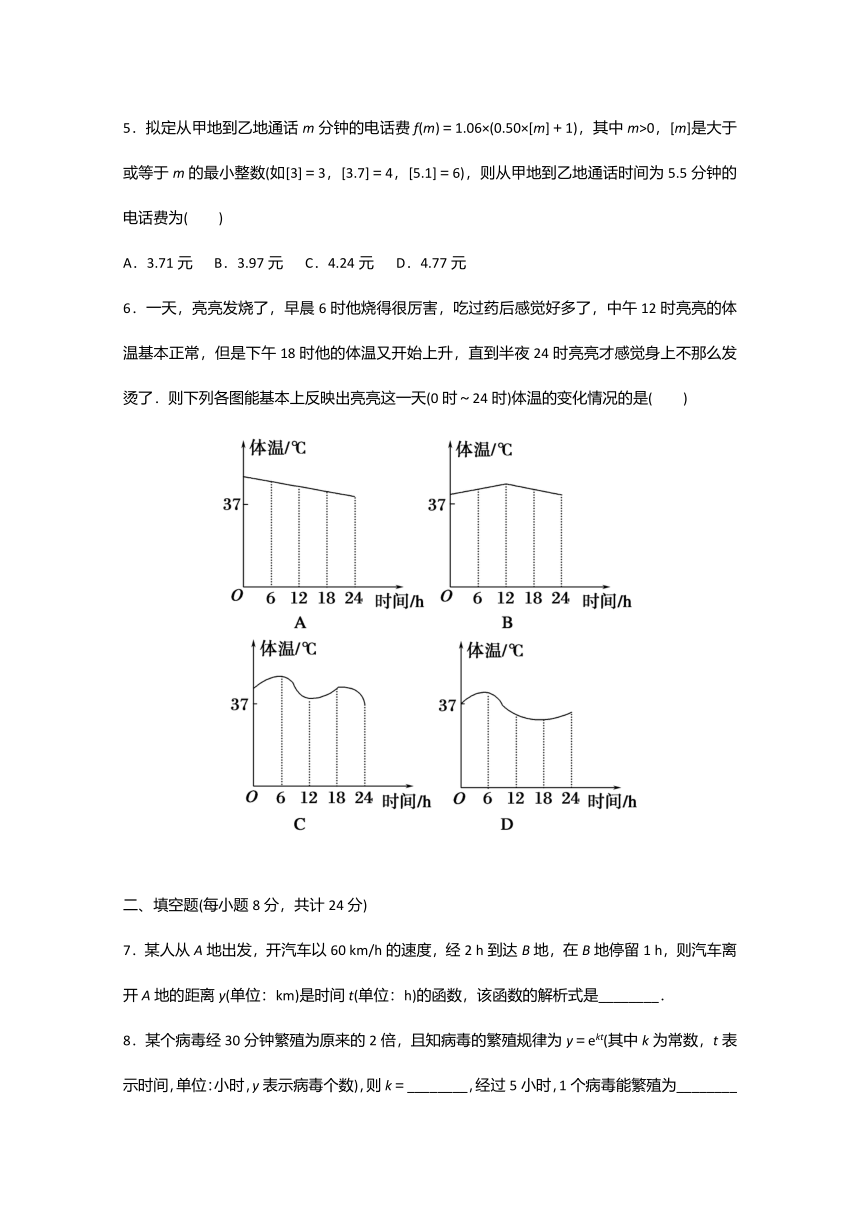
1.小明的父亲饭后出去散步,从家中走20分钟到一个离家900米的报亭看10分钟报纸后,用20分钟返回家里,下面图形中能表示小明的父亲离开家的时间与距离之间的关系的是( )
2.某产品的利润y(元)关于产量x(件)的函数关系式为y=3x+4,则当产量为4件时,利润y等于( )
A.4元 B.16元 C.85元 D.不确定
3.在一次数学实验中,采集到如下一组数据:
x -2.0 -1.0 0 1.0 2.0 3.0
y 0.24 0.51 1 2.02 3.98 8.02
则x,y的函数关系与下列哪类函数最接近?(其中a,b为待定系数)( )
A.y=a+bx B.y=bx C.y=ax2+b D.y=
4.2011年全球经济复苏,据统计某地区1月、2月、3月的用工人数分别为0.2万人,0.4万人和0.76万人,则该地区这三个月的用工人数y万人关于月数x的函数关系近似的是( )
A.y=0.2x B.y=(x2+2x) C.y= D.y=0.2+log16x
5.拟定从甲地到乙地通话m分钟的电话费f(m)=1.06×(0.50×[m]+1),其中m>0,[m]是大于或等于m的最小整数(如[3]=3,[3.7]=4,[5.1]=6),则从甲地到乙地通话时间为5.5分钟的电话费为( )
A.3.71元 B.3.97元 C.4.24元 D.4.77元
6.一天,亮亮发烧了,早晨6时他烧得很厉害,吃过药后感觉好多了,中午12时亮亮的体温基本正常,但是下午18时他的体温又开始上升,直到半夜24时亮亮才感觉身上不那么发烫了.则下列各图能基本上反映出亮亮这一天(0时~24时)体温的变化情况的是( )
二、填空题(每小题8分,共计24分)
7.某人从A地出发,开汽车以60 km/h的速度,经2 h到达B地,在B地停留1 h,则汽车离开A地的距离y(单位:km)是时间t(单位:h)的函数,该函数的解析式是________.
8.某个病毒经30分钟繁殖为原来的2倍,且知病毒的繁殖规律为y=ekt(其中k为常数,t表示时间,单位:小时,y表示病毒个数),则k=________,经过5小时,1个病毒能繁殖为________个.
9.为了预防甲流的发生,某学校决定对教室用药熏消毒法进行消毒,根据药学原理,从药物释放开始,每立方米空气中的含药量y(毫克)与时间t(小时)之间的函数关系式为y=据测定,当空气中每立方米的含药量降低到0.25毫克以下时,学生方可进教室学习.那么从药物释放开始,至少需要经过________小时后,学生才能回到教室.
三、解答题(共计40分)
10.(10分)某市原来民用电价为0.52元/kW·h.换装分时电表后,峰时段(早上八点到晚上九点)的电价为0.55元/kW·h,谷时段(晚上九点到次日早上八点)的电价为0.35元/kW·h.对于一个平均每日用电量为200 kW·h的家庭,要使节省的电费不少于原来电费的10%,则这个家庭每月在峰时段的平均用电量至多为多少?
11.(15分)沿海地区某村在2011年底共有人口1480人,全年工农业生产总值为3180万,从2012年起计划10年内该村的总产值每年增加60万元,人口每年净增a人,设从2012年起的第x年(2012年为第一年)该村人均产值为y万元.
(1)写出y与x之间的函数关系式;
(2)为使该村的人均产值10年内每年都有增长,那么该村每年人口的净增长不能超过多少人?
[创新应用]
12.(15分)东日本发生里氏9.0级大地震,地震引发海啸,造成大量人员伤亡和财产损失,并引发核泄漏.你知道地震的震级是如何确定的吗?20世纪30年代,查尔斯·里克特制定了一种表明地震能量大小的尺度,就是使用测震仪衡量地震能量的等级,地震能量越大,测震仪记录的地震曲线的振幅就越大.这就是我们常说的里氏震级M,其计算公式为:M=lgA-lgA0,其中,A是被测地震的最大振幅,A0是“标准地震”的振幅(使用标准地震振幅是为了修正测震仪距实际震中距离造成的偏差.).
(1)假设在一次地震中,一个距离震中100千米的测震仪记录的地震最大振幅是20,此时标准地震的振幅是0.001,计算这次地震的震级(精确到0.1)(已知lg2≈0.3010)
(2)5级地震给人的震感已比较明显,计算7.6级地震最大振幅是5级地震最大振幅的多少倍(精确到1).(已知102.6≈398)
答案
一、选择题(每小题6分,共计36分)
1.答案:D
2.答案:C
解析:当x=4时,y=34+4=85(元).
3.答案:B
解析:画出散点图如图1所示.
图1
由散点图可知选项B正确.
4.答案:C
解析:将x=1,2,3代入y=,求出的y值与实际用工人数量接近,故选C.
5.答案:C
解析:[5.5]=6,∴f(5.5)=1.06×(0.50×[5.5]+1)=1.06×(0.50×6+1)=1.06×(3+1)=4.24(元).
6.答案:C
解析:从0时到6时,体温上升,图象是上升的,排除选项A;从6时到12时,体温下降,图象是下降的,排除选项B;从12时到18时,体温上升,图象是上升的,排除选项D.
二、填空题(每小题8分,共计24分)
7.答案:y=
解析:当0≤t≤2时,y=60t;当28.答案:2ln2 1024
解析:当t=0.5时,y=2,∴2=e eq \s\up15( ) .∴k=2ln2.∴y=e2tln2.
∴当t=5时,y=e10ln2=210=1024.
9.答案:0.6
解析:由题意可得y≤0.25=,即得或
得0≤t≤或t≥0.6.因为前0.1个小时药物浓度是逐渐增大的,
故至少需要经过0.6小时后才可回教室.
三、解答题(共计40分)
10.解:原来电费y1=0.52×200=104(元).
设峰时用电量为x kW·h,电费为y元,谷时段用电量为(200-x) kW·h.
则y=0.55x+0.35(200-x)≤(1-10%)y1,即0.55x+70-0.35x≤93.6,
则0.2x≤23.6,∴x≤118,
即这个家庭每月在峰时段的平均用电量至多为118 kW·h.
11.解:(1)依题意得第x年该村的工农业生产总值为(3180+60x)万元,而该村第x年的人口总数为(1480+ax)人,
∴y=(1≤x≤10).
(2)y==(1+),
为使该村的人均产值年年都有增长,则在1≤x≤10内,y=f(x)为增函数,
则有53-<0,∴a<≈27.9.
又∵a∈N*,∴a的最大值是27.
即该村每年人口的净增不能超过27人.
12.解:(1)M=lg20-lg0.001=lg=lg20 000=lg2+lg104≈4.3.
因此,这是一次约为里氏4.3级的地震.
(2)由M=lgA-lgA0,可得M=lg =10M A=A0·10M.
当M=7.6时,地震的最大振幅为A1=A0·107.6;
当M=5时,地震的最大振幅为A2=A0·105.
所以,两次地震的最大振幅之比是==107.6-5=102.6≈398.
7.6级地震的最大振幅大约是5级地震最大振幅的398倍.
PAGE
时间:45分钟 分值:100分
一、选择题(每小题6分,共计36分)
1.小明的父亲饭后出去散步,从家中走20分钟到一个离家900米的报亭看10分钟报纸后,用20分钟返回家里,下面图形中能表示小明的父亲离开家的时间与距离之间的关系的是( )
2.某产品的利润y(元)关于产量x(件)的函数关系式为y=3x+4,则当产量为4件时,利润y等于( )
A.4元 B.16元 C.85元 D.不确定
3.在一次数学实验中,采集到如下一组数据:
x -2.0 -1.0 0 1.0 2.0 3.0
y 0.24 0.51 1 2.02 3.98 8.02
则x,y的函数关系与下列哪类函数最接近?(其中a,b为待定系数)( )
A.y=a+bx B.y=bx C.y=ax2+b D.y=
4.2011年全球经济复苏,据统计某地区1月、2月、3月的用工人数分别为0.2万人,0.4万人和0.76万人,则该地区这三个月的用工人数y万人关于月数x的函数关系近似的是( )
A.y=0.2x B.y=(x2+2x) C.y= D.y=0.2+log16x
5.拟定从甲地到乙地通话m分钟的电话费f(m)=1.06×(0.50×[m]+1),其中m>0,[m]是大于或等于m的最小整数(如[3]=3,[3.7]=4,[5.1]=6),则从甲地到乙地通话时间为5.5分钟的电话费为( )
A.3.71元 B.3.97元 C.4.24元 D.4.77元
6.一天,亮亮发烧了,早晨6时他烧得很厉害,吃过药后感觉好多了,中午12时亮亮的体温基本正常,但是下午18时他的体温又开始上升,直到半夜24时亮亮才感觉身上不那么发烫了.则下列各图能基本上反映出亮亮这一天(0时~24时)体温的变化情况的是( )
二、填空题(每小题8分,共计24分)
7.某人从A地出发,开汽车以60 km/h的速度,经2 h到达B地,在B地停留1 h,则汽车离开A地的距离y(单位:km)是时间t(单位:h)的函数,该函数的解析式是________.
8.某个病毒经30分钟繁殖为原来的2倍,且知病毒的繁殖规律为y=ekt(其中k为常数,t表示时间,单位:小时,y表示病毒个数),则k=________,经过5小时,1个病毒能繁殖为________个.
9.为了预防甲流的发生,某学校决定对教室用药熏消毒法进行消毒,根据药学原理,从药物释放开始,每立方米空气中的含药量y(毫克)与时间t(小时)之间的函数关系式为y=据测定,当空气中每立方米的含药量降低到0.25毫克以下时,学生方可进教室学习.那么从药物释放开始,至少需要经过________小时后,学生才能回到教室.
三、解答题(共计40分)
10.(10分)某市原来民用电价为0.52元/kW·h.换装分时电表后,峰时段(早上八点到晚上九点)的电价为0.55元/kW·h,谷时段(晚上九点到次日早上八点)的电价为0.35元/kW·h.对于一个平均每日用电量为200 kW·h的家庭,要使节省的电费不少于原来电费的10%,则这个家庭每月在峰时段的平均用电量至多为多少?
11.(15分)沿海地区某村在2011年底共有人口1480人,全年工农业生产总值为3180万,从2012年起计划10年内该村的总产值每年增加60万元,人口每年净增a人,设从2012年起的第x年(2012年为第一年)该村人均产值为y万元.
(1)写出y与x之间的函数关系式;
(2)为使该村的人均产值10年内每年都有增长,那么该村每年人口的净增长不能超过多少人?
[创新应用]
12.(15分)东日本发生里氏9.0级大地震,地震引发海啸,造成大量人员伤亡和财产损失,并引发核泄漏.你知道地震的震级是如何确定的吗?20世纪30年代,查尔斯·里克特制定了一种表明地震能量大小的尺度,就是使用测震仪衡量地震能量的等级,地震能量越大,测震仪记录的地震曲线的振幅就越大.这就是我们常说的里氏震级M,其计算公式为:M=lgA-lgA0,其中,A是被测地震的最大振幅,A0是“标准地震”的振幅(使用标准地震振幅是为了修正测震仪距实际震中距离造成的偏差.).
(1)假设在一次地震中,一个距离震中100千米的测震仪记录的地震最大振幅是20,此时标准地震的振幅是0.001,计算这次地震的震级(精确到0.1)(已知lg2≈0.3010)
(2)5级地震给人的震感已比较明显,计算7.6级地震最大振幅是5级地震最大振幅的多少倍(精确到1).(已知102.6≈398)
答案
一、选择题(每小题6分,共计36分)
1.答案:D
2.答案:C
解析:当x=4时,y=34+4=85(元).
3.答案:B
解析:画出散点图如图1所示.
图1
由散点图可知选项B正确.
4.答案:C
解析:将x=1,2,3代入y=,求出的y值与实际用工人数量接近,故选C.
5.答案:C
解析:[5.5]=6,∴f(5.5)=1.06×(0.50×[5.5]+1)=1.06×(0.50×6+1)=1.06×(3+1)=4.24(元).
6.答案:C
解析:从0时到6时,体温上升,图象是上升的,排除选项A;从6时到12时,体温下降,图象是下降的,排除选项B;从12时到18时,体温上升,图象是上升的,排除选项D.
二、填空题(每小题8分,共计24分)
7.答案:y=
解析:当0≤t≤2时,y=60t;当2
解析:当t=0.5时,y=2,∴2=e eq \s\up15( ) .∴k=2ln2.∴y=e2tln2.
∴当t=5时,y=e10ln2=210=1024.
9.答案:0.6
解析:由题意可得y≤0.25=,即得或
得0≤t≤或t≥0.6.因为前0.1个小时药物浓度是逐渐增大的,
故至少需要经过0.6小时后才可回教室.
三、解答题(共计40分)
10.解:原来电费y1=0.52×200=104(元).
设峰时用电量为x kW·h,电费为y元,谷时段用电量为(200-x) kW·h.
则y=0.55x+0.35(200-x)≤(1-10%)y1,即0.55x+70-0.35x≤93.6,
则0.2x≤23.6,∴x≤118,
即这个家庭每月在峰时段的平均用电量至多为118 kW·h.
11.解:(1)依题意得第x年该村的工农业生产总值为(3180+60x)万元,而该村第x年的人口总数为(1480+ax)人,
∴y=(1≤x≤10).
(2)y==(1+),
为使该村的人均产值年年都有增长,则在1≤x≤10内,y=f(x)为增函数,
则有53-<0,∴a<≈27.9.
又∵a∈N*,∴a的最大值是27.
即该村每年人口的净增不能超过27人.
12.解:(1)M=lg20-lg0.001=lg=lg20 000=lg2+lg104≈4.3.
因此,这是一次约为里氏4.3级的地震.
(2)由M=lgA-lgA0,可得M=lg =10M A=A0·10M.
当M=7.6时,地震的最大振幅为A1=A0·107.6;
当M=5时,地震的最大振幅为A2=A0·105.
所以,两次地震的最大振幅之比是==107.6-5=102.6≈398.
7.6级地震的最大振幅大约是5级地震最大振幅的398倍.
PAGE
