1.1.3集合的基本运算 第2课时课件(38张)
文档属性
| 名称 | 1.1.3集合的基本运算 第2课时课件(38张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-30 00:00:00 | ||
图片预览








文档简介
(共38张PPT)
人教版 必修1
第一章 集合与函数概念
1.1 集合
1.1.3 集合的基本运算
第二课时 补集
如果你所在班级共有60名同学,要求你从中选出56名同学参加体操比赛,你如何完成这件事呢?
你不可能直接去找张三、李四、王五、……,一一确定出谁去参加吧?如果按这种方法做这件事情,可就麻烦多了.若确定出4位不参加比赛的同学,剩下的56名同学都参加,问题可就简单多了.不要小看这个问题的解决方法,它可是这节内容(补集)的现实基础.
情境引入
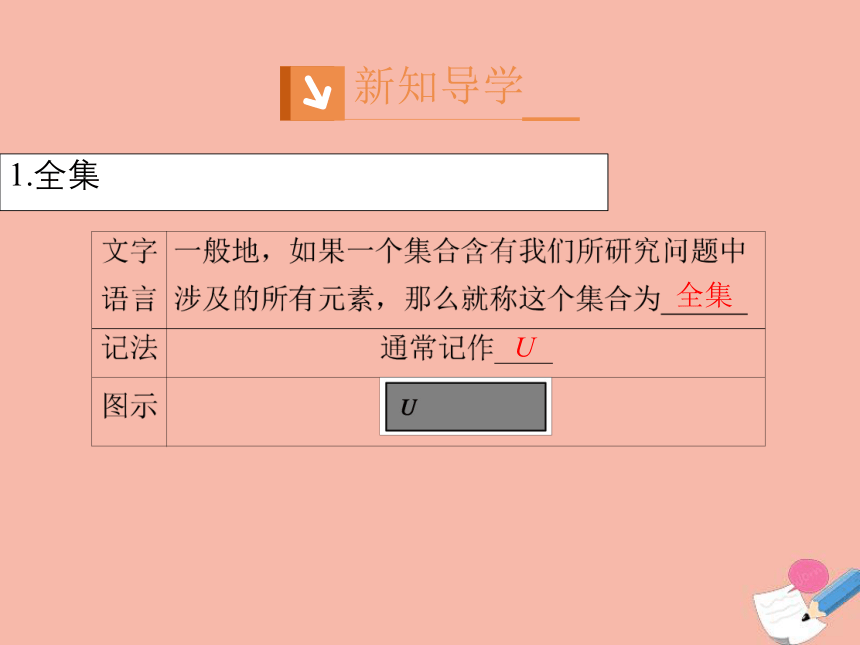
1.全集
全集
U
新知导学
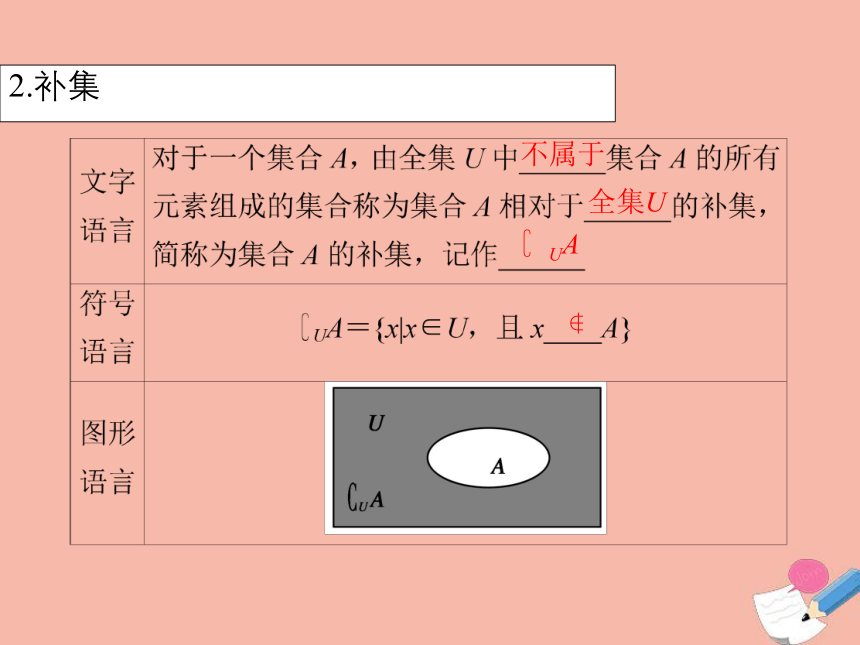
2.补集
不属于
全集U
UA
预习自测
[答案] D
[解析] ∵U={1,2,3,4,5},∴ UB={1,3,4},∴A∩ UB={1,3}.
[答案] 5
[解析] 由 AB={5}知5∈A,∴m=5.
[答案] {钝角三角形或锐角三角形}
[解析] {三角形}={直角三角形,锐角三角形,钝角三角形}结合补集的定义求得.
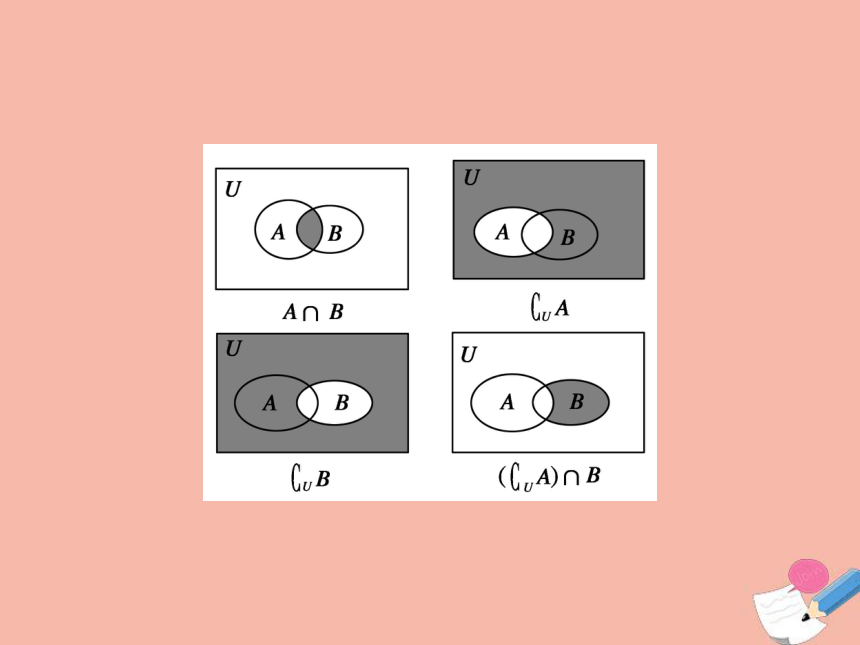
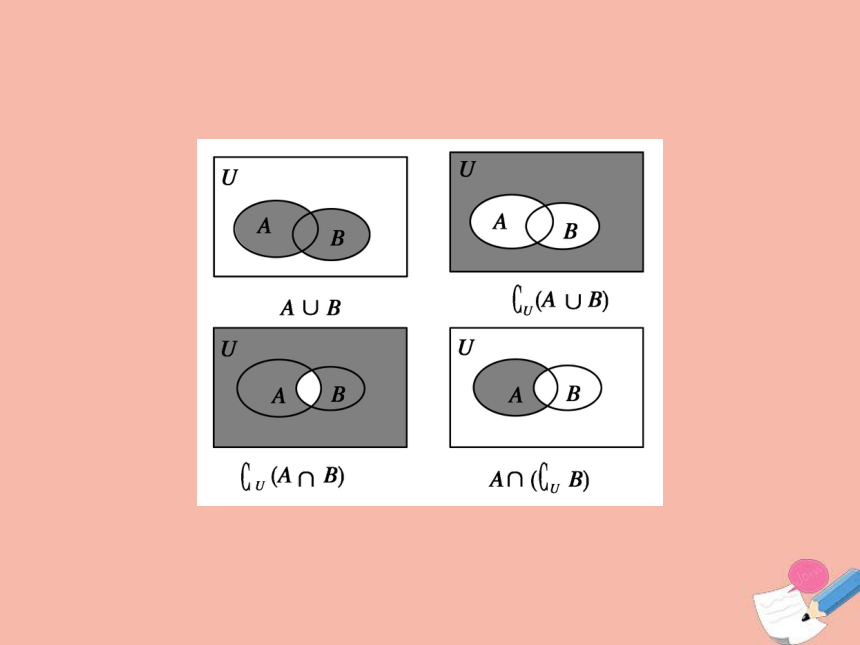
补集的基本运算
[规律总结] 求集合补集的基本方法及处理技巧
(1)基本方法:定义法.
(2)两种处理技巧:
①当集合用列举法表示时,可借助Venn图求解.
②当集合是用描述表示的连续数集时,可借助数轴,利用数轴分析求解.
练习1
[答案] (1)B (2)2
交集、并集、补集的综合运算
[思路分析] (1)有限集利用Venn图求解;(2)无限集利用数轴,分别表示出全集U及集合A,B,先求出 UA及 UB,再求解.
练习2
[答案] (1){1,2,3} (2)B
补集性质的应用
[规律总结] “正难则反”策略是指当某一问题从正面解决较困难时,我们可以从其反面入手解决.已知全集U,求子集A,若直接求A困难,可运用“正难则反”策略先求 UA,再由 U( UA)=A求A.
补集作为一种思想方法给我们研究问题开辟了新思路,今后要有意识地去体会并运用.在顺向思维受阻时,改用逆向思维,可能“柳暗花明”.从这个意义上讲,补集思想具有转换研究对象的功能,这是转化思想的又一体现.
练习3
误区警示
q=6时,A={2,3}, UA={1,4,5}.
q=4时,A={1,4}, UA={2,3,5}.
所以q=0时, UA={1,2,3,4},
q=4时, UA={2,3,5},
q=6时, UA={1,4,5}.
[错因分析] 错解中没有注意到A U,当q=0时,A={0,5}U,另外,当A= 时, UA=U,此时方程x2-5x+q=0无实数解.
练习4
[答案] B
[解析] 由补集定义并结合数轴易知 RA={x|x<0或x>6},故选B.
当堂检测
[答案] C
[解析] 利用数轴分析,可知A={x|x≥2}.
[答案] D
[解析] ∵A∪B={x|x≤0或x≥1},∴ U(A∪B)={x|0<x<1}.故选D.
[答案] {7,9}
[解析] 由题意,得U={1,2,3,4,5,6,7,8,9,10},故 UA={4,6,7,9,10},所以( UA)∩B={7,9}.
人教版 必修1
第一章 集合与函数概念
1.1 集合
1.1.3 集合的基本运算
第二课时 补集
如果你所在班级共有60名同学,要求你从中选出56名同学参加体操比赛,你如何完成这件事呢?
你不可能直接去找张三、李四、王五、……,一一确定出谁去参加吧?如果按这种方法做这件事情,可就麻烦多了.若确定出4位不参加比赛的同学,剩下的56名同学都参加,问题可就简单多了.不要小看这个问题的解决方法,它可是这节内容(补集)的现实基础.
情境引入
1.全集
全集
U
新知导学
2.补集
不属于
全集U
UA
预习自测
[答案] D
[解析] ∵U={1,2,3,4,5},∴ UB={1,3,4},∴A∩ UB={1,3}.
[答案] 5
[解析] 由 AB={5}知5∈A,∴m=5.
[答案] {钝角三角形或锐角三角形}
[解析] {三角形}={直角三角形,锐角三角形,钝角三角形}结合补集的定义求得.
补集的基本运算
[规律总结] 求集合补集的基本方法及处理技巧
(1)基本方法:定义法.
(2)两种处理技巧:
①当集合用列举法表示时,可借助Venn图求解.
②当集合是用描述表示的连续数集时,可借助数轴,利用数轴分析求解.
练习1
[答案] (1)B (2)2
交集、并集、补集的综合运算
[思路分析] (1)有限集利用Venn图求解;(2)无限集利用数轴,分别表示出全集U及集合A,B,先求出 UA及 UB,再求解.
练习2
[答案] (1){1,2,3} (2)B
补集性质的应用
[规律总结] “正难则反”策略是指当某一问题从正面解决较困难时,我们可以从其反面入手解决.已知全集U,求子集A,若直接求A困难,可运用“正难则反”策略先求 UA,再由 U( UA)=A求A.
补集作为一种思想方法给我们研究问题开辟了新思路,今后要有意识地去体会并运用.在顺向思维受阻时,改用逆向思维,可能“柳暗花明”.从这个意义上讲,补集思想具有转换研究对象的功能,这是转化思想的又一体现.
练习3
误区警示
q=6时,A={2,3}, UA={1,4,5}.
q=4时,A={1,4}, UA={2,3,5}.
所以q=0时, UA={1,2,3,4},
q=4时, UA={2,3,5},
q=6时, UA={1,4,5}.
[错因分析] 错解中没有注意到A U,当q=0时,A={0,5}U,另外,当A= 时, UA=U,此时方程x2-5x+q=0无实数解.
练习4
[答案] B
[解析] 由补集定义并结合数轴易知 RA={x|x<0或x>6},故选B.
当堂检测
[答案] C
[解析] 利用数轴分析,可知A={x|x≥2}.
[答案] D
[解析] ∵A∪B={x|x≤0或x≥1},∴ U(A∪B)={x|0<x<1}.故选D.
[答案] {7,9}
[解析] 由题意,得U={1,2,3,4,5,6,7,8,9,10},故 UA={4,6,7,9,10},所以( UA)∩B={7,9}.
