青岛版数学九年级上册 3.3圆周角课件(共10张PPT)
文档属性
| 名称 | 青岛版数学九年级上册 3.3圆周角课件(共10张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 181.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-29 14:37:22 | ||
图片预览


文档简介
(共10张PPT)
3.3圆周角(3)
学习目标
理解并掌握圆内接四边形的概念及性质并学会运用. (重点)
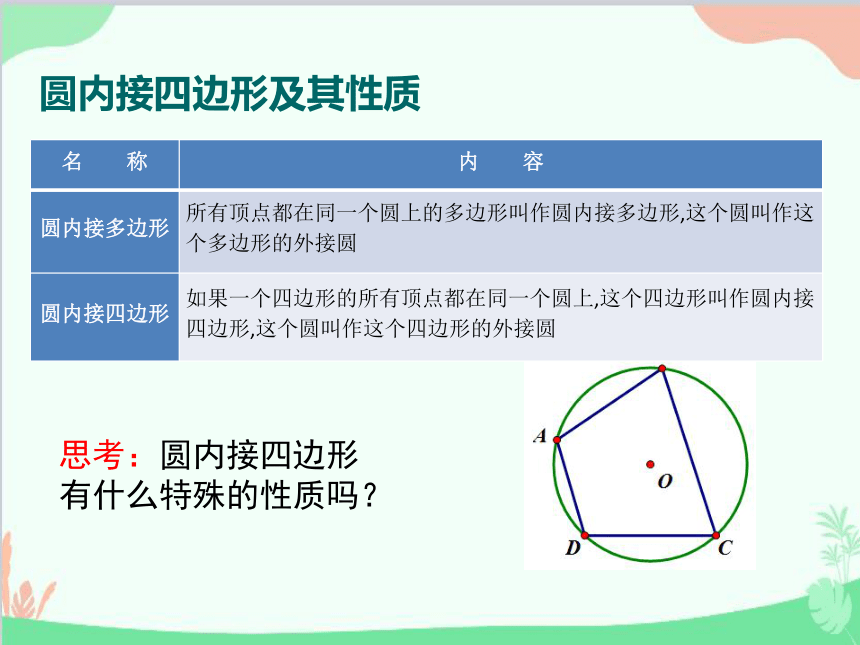
圆内接四边形及其性质
思考:圆内接四边形有什么特殊的性质吗?
名 称 内 容
圆内接多边形 所有顶点都在同一个圆上的多边形叫作圆内接多边形,这个圆叫作这
个多边形的外接圆
圆内接四边形 如果一个四边形的所有顶点都在同一个圆上,这个四边形叫作圆内接
四边形,这个圆叫作这个四边形的外接圆
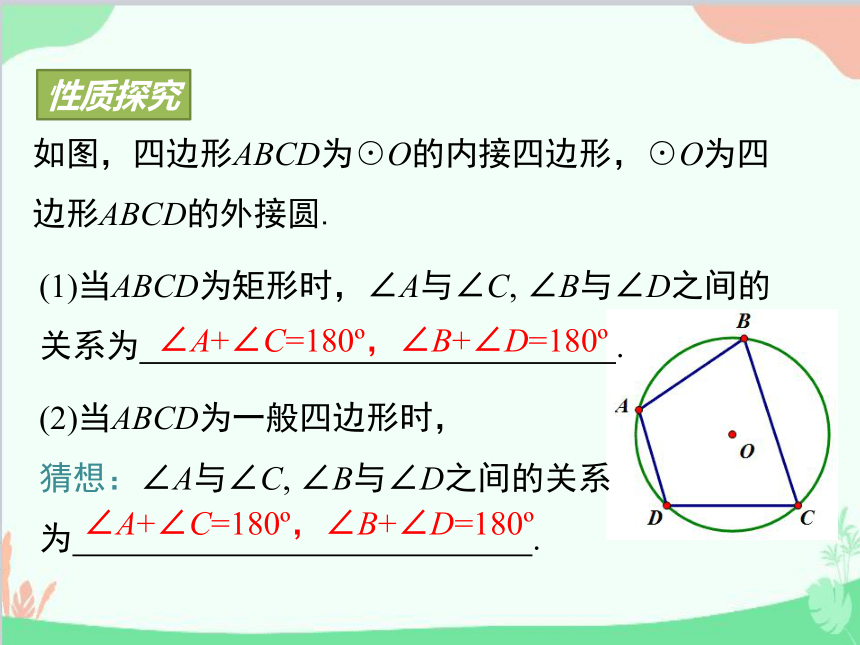
如图,四边形ABCD为☉O的内接四边形,☉O为四边形ABCD的外接圆.
(2)当ABCD为一般四边形时,
猜想:∠A与∠C, ∠B与∠D之间的关系为 .
∠A+∠C=180 ,∠B+∠D=180
(1)当ABCD为矩形时,∠A与∠C, ∠B与∠D之间的关系为 .
∠A+∠C=180 ,∠B+∠D=180
性质探究
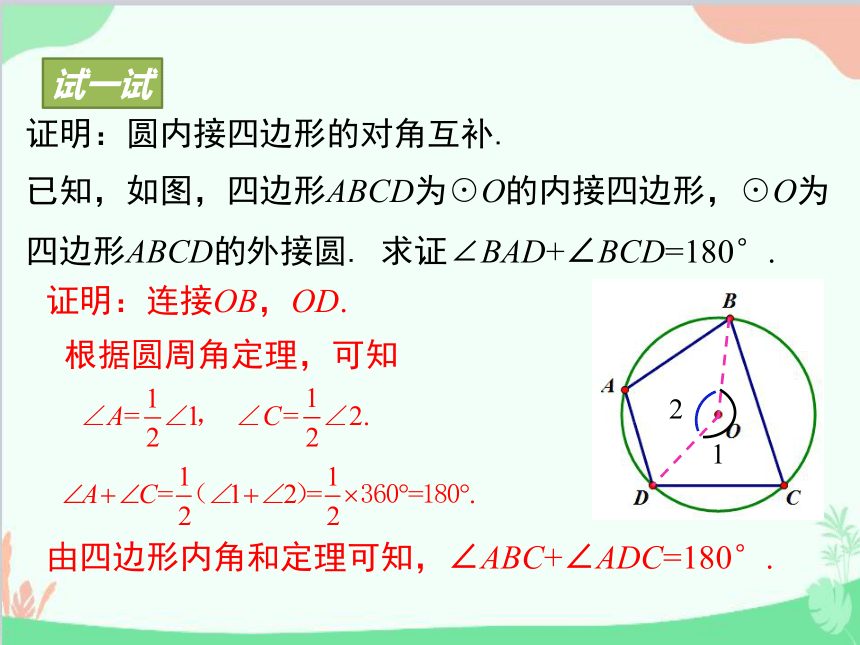
证明:圆内接四边形的对角互补.
已知,如图,四边形ABCD为☉O的内接四边形,☉O为四边形ABCD的外接圆. 求证∠BAD+∠BCD=180°.
证明:连接OB,OD.
根据圆周角定理,可知
1
2
由四边形内角和定理可知,∠ABC+∠ADC=180°.
试一试
圆内接四边形的对角互补.
推论4
要点归纳
C
O
D
B
A
∵∠A+∠DCB=180°,
E
∠DCB+∠DCE=180°.
∴∠A=∠DCE.
如图,∠DCE是圆内接四边形ABCD的一个外角,∠A与∠DCE的大小有何关系?
想一想
1.四边形ABCD是⊙O的内接四边形,且∠A=110°,∠B=80°,则∠C= ,∠D= .
2.⊙O的内接四边形ABCD中,∠A∶∠B∶∠C=1∶2∶3 ,则∠D= .
70
100
90
练一练
3. 如图,在⊙O的内接四边形ABCD中,∠BOD=120°,那么∠BCD是( )
A.120° B.100°
C.80° D.60°
解析:∵∠BOD=120°,∴∠A=60°,
∴∠C=180°-60°=120°,故选A.
A
圆周角定理
推论4
圆内接四边形的对角互补.
课堂小结
3.3圆周角(3)
学习目标
理解并掌握圆内接四边形的概念及性质并学会运用. (重点)
圆内接四边形及其性质
思考:圆内接四边形有什么特殊的性质吗?
名 称 内 容
圆内接多边形 所有顶点都在同一个圆上的多边形叫作圆内接多边形,这个圆叫作这
个多边形的外接圆
圆内接四边形 如果一个四边形的所有顶点都在同一个圆上,这个四边形叫作圆内接
四边形,这个圆叫作这个四边形的外接圆
如图,四边形ABCD为☉O的内接四边形,☉O为四边形ABCD的外接圆.
(2)当ABCD为一般四边形时,
猜想:∠A与∠C, ∠B与∠D之间的关系为 .
∠A+∠C=180 ,∠B+∠D=180
(1)当ABCD为矩形时,∠A与∠C, ∠B与∠D之间的关系为 .
∠A+∠C=180 ,∠B+∠D=180
性质探究
证明:圆内接四边形的对角互补.
已知,如图,四边形ABCD为☉O的内接四边形,☉O为四边形ABCD的外接圆. 求证∠BAD+∠BCD=180°.
证明:连接OB,OD.
根据圆周角定理,可知
1
2
由四边形内角和定理可知,∠ABC+∠ADC=180°.
试一试
圆内接四边形的对角互补.
推论4
要点归纳
C
O
D
B
A
∵∠A+∠DCB=180°,
E
∠DCB+∠DCE=180°.
∴∠A=∠DCE.
如图,∠DCE是圆内接四边形ABCD的一个外角,∠A与∠DCE的大小有何关系?
想一想
1.四边形ABCD是⊙O的内接四边形,且∠A=110°,∠B=80°,则∠C= ,∠D= .
2.⊙O的内接四边形ABCD中,∠A∶∠B∶∠C=1∶2∶3 ,则∠D= .
70
100
90
练一练
3. 如图,在⊙O的内接四边形ABCD中,∠BOD=120°,那么∠BCD是( )
A.120° B.100°
C.80° D.60°
解析:∵∠BOD=120°,∴∠A=60°,
∴∠C=180°-60°=120°,故选A.
A
圆周角定理
推论4
圆内接四边形的对角互补.
课堂小结
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
