2021-2022学年高一上学期数学人教A版(2019)必修第一册4.5.函数的应用(二)课件(共20张PPT)
文档属性
| 名称 | 2021-2022学年高一上学期数学人教A版(2019)必修第一册4.5.函数的应用(二)课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 288.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-27 00:00:00 | ||
图片预览




文档简介
(共20张PPT)
在数学的发展史上,方程的求解一直都是数学发展、数学教育和数学研究的最核心环节之一.
我国古代数学家已比较系统地解决了部分方程求解的问题. 约公元50年—100年编成的《九章算术》,就给出了求一次方程、二次方程和正系数三次方程根的具体方法…
前面我们学习了函数的知识,那么函数和方程有什么关系呢?面对一个实际问题,我们又该选择什么函数模型来加以解决呢?这正是函数的应用(二)所要解决的问题!让我们先从下面的问题开始吧!
4.5 函数的应用(二)
4.5.1函数的零点与方程的解
问题1:下列方程有实数根吗?
一.生成概念
(1) x2-2x-3=0
(2) x2-2x+1=0
(3) x2-2x+3=0
追问 还有其它方法判断方程
x2-2x-3=0有实数根吗?
f(x)=x2-2x-3
方程
x2-2x+1=0
x2-2x+3=0
y= x2-2x-3
y= x2-2x+1
函数
函
数
的
图
象
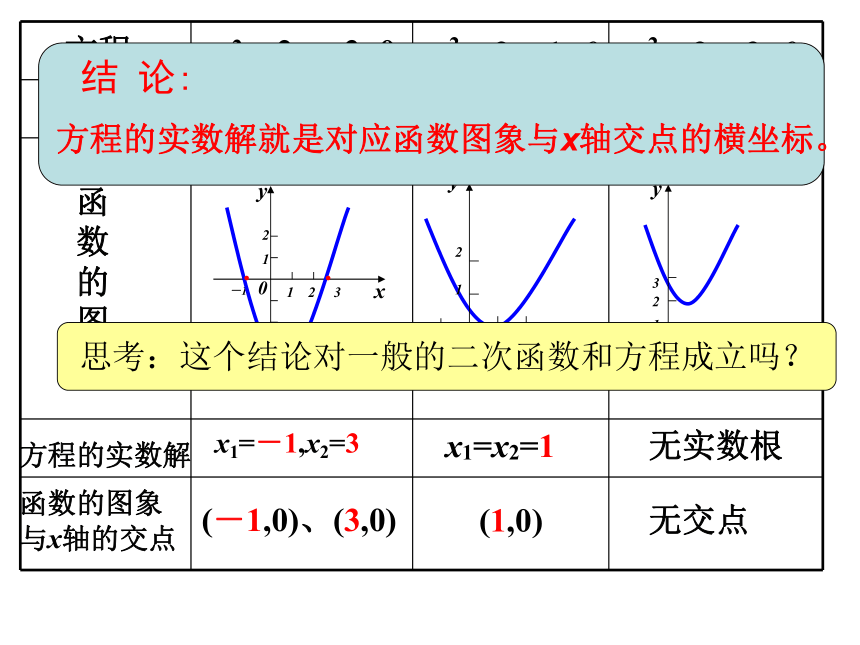
方程的实数解
x1=-1,x2=3
x1=x2=1
无实数根
函数的图象
与x轴的交点
(-1,0)、(3,0)
(1,0)
无交点
x2-2x-3=0
x
y
0
-1
3
2
1
1
2
.
.
x
y
0
-1
3
2
1
1
2
3
.
y
x
0
2
1
1
2
y= x2-2x+3
方程的实数解就是对应函数图象与x轴交点的横坐标。
结 论:
思考:这个结论对一般的二次函数和方程成立吗?
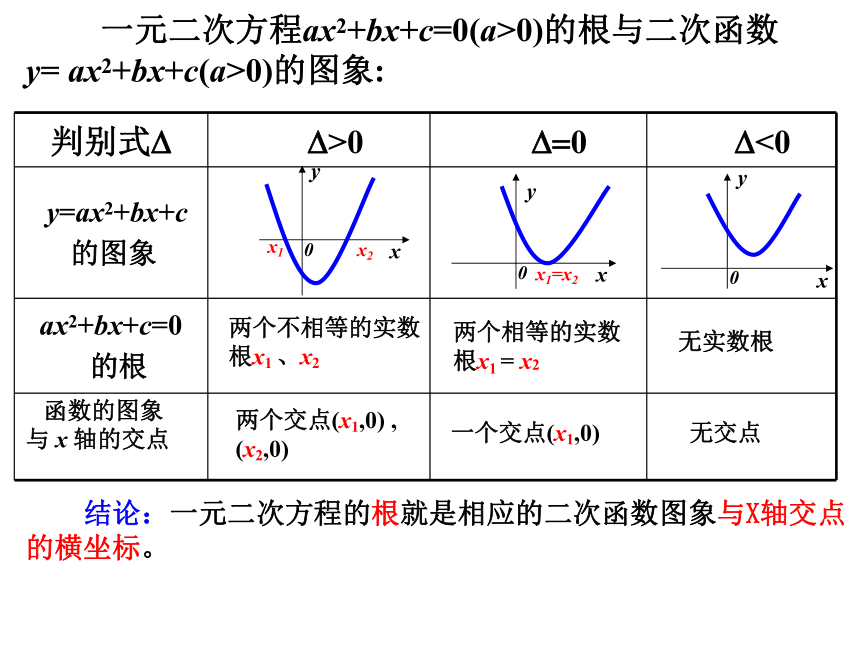
判别式 >0 0 <0
y=ax2+bx+c 的图象
ax2+bx+c=0 的根
x
y
x1
x2
0
x
y
0
x
y
0
函数的图象
与 x 轴的交点
两个交点(x1,0) , (x2,0)
无交点
两个相等的实数根x1 = x2
无实数根
两个不相等的实数根x1 、x2
结论:一元二次方程的根就是相应的二次函数图象与X轴交点的横坐标。
一元二次方程ax2+bx+c=0(a>0)的根与二次函数
y= ax2+bx+c(a>0)的图象:
x1=x2
一个交点(x1,0)
1.函数的零点
对于函数y=f(x), 使f(x)=0的实数x
叫做函数y=f(x)的零点.
注意:(1) 零点是一个实数
零点是一个点吗
推广到更一般的情况:
归纳:
1.代数法:函数零点就是相应方程的实数根,可解相应方程求函数的零点.
2.几何法:作出函数y=f(x)的图象,确定图象与x轴的交点的横坐标,求函数的零点.
1. 函数f(x)=(x - 1)(x +2)的零点是( )
A.(1,0),(- 2,0), B. 1, - 2
C.(0,1),(0, - 2), D. - 1, 2
练习1
2. (1)f(x)= 2x-1的零点是________.
B
0
(2)函数f(x)=
的零点是________.
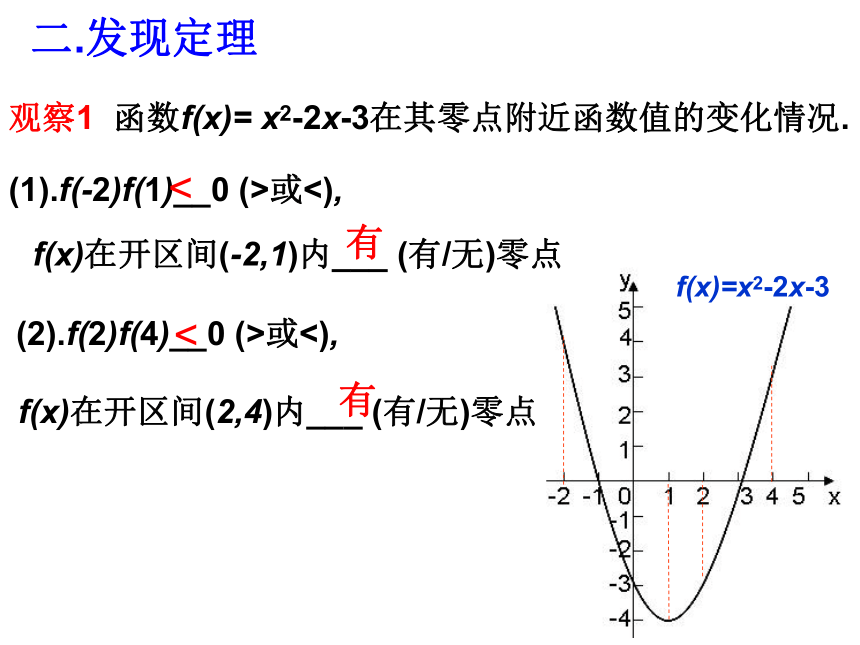
观察1 函数f(x)= x2-2x-3在其零点附近函数值的变化情况.
(1).f(-2)f(1)__0 (>或<),
<
(2).f(2)f(4)__0 (>或<),
<
二.发现定理
f(x)=x2-2x-3
f(x)在开区间(-2,1)内___ (有/无)零点
f(x)在开区间(2,4)内___ (有/无)零点
有
有
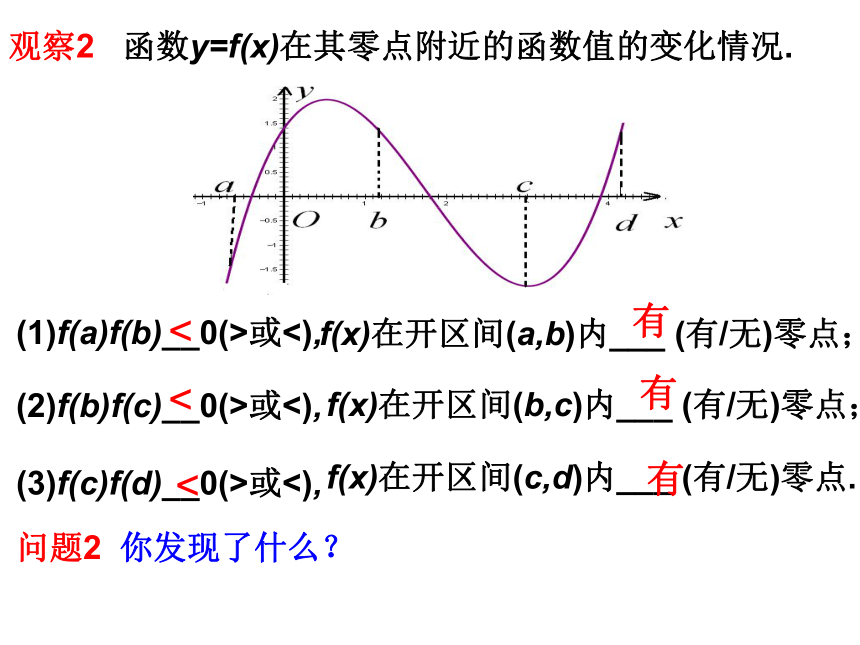
观察2 函数y=f(x)在其零点附近的函数值的变化情况.
(1)f(a)f(b)__0(>或<),
<
f(x)在开区间(a,b)内___ (有/无)零点;
<
<
有
(2)f(b)f(c)__0(>或<),
f(x)在开区间(b,c)内___ (有/无)零点;
有
(3)f(c)f(d)__0(>或<),
f(x)在开区间(c,d)内___ (有/无)零点.
有
问题2 你发现了什么?
如果函数y=f(x)在区间[a,b]上
有f(a)f(b)﹤0,那么函 数y=f(x)在(a,b)内有零点,即存在c∈ (a,b),使得f(c)=0,这个c也就是方程f(x)=0的根.
的图象是连续不断的一条曲线,并且
猜想:
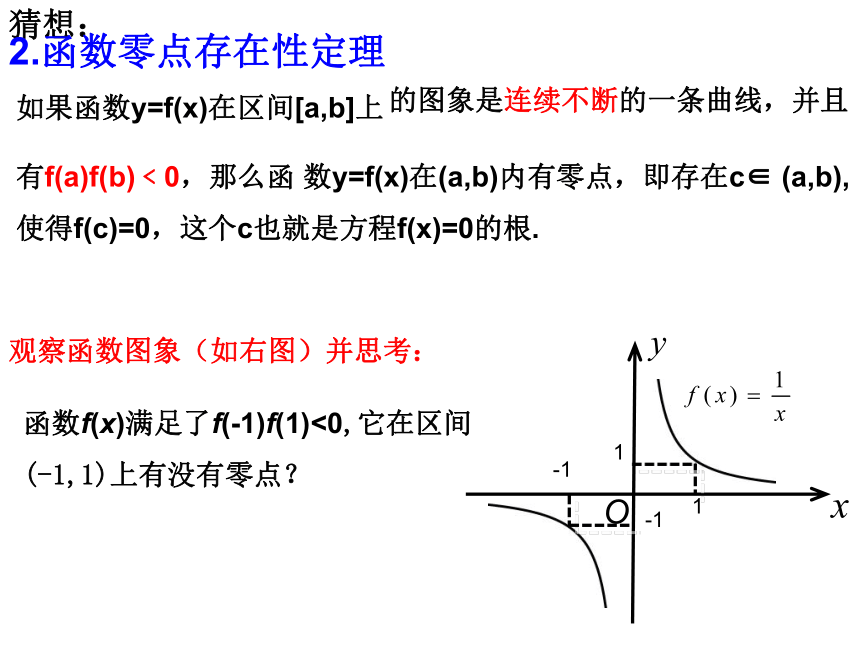
2.函数零点存在性定理
观察函数图象(如右图)并思考:
O
-1
1
-1
1
函数f(x)满足了f(-1)f(1)<0,它在区间
(-1,1)上有没有零点?
至少有一个,
可以有多个.
注意: (1)两个前提条件缺一不可.
(2)“有零点”是指有几个零点呢?
只有一个吗?
(3)再加上什么条件就“有且仅有一个零点”呢?
x
y
0
如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且f(a)f(b)﹤0,并且是单调函数,那么函 数y=f(x)在(a,b)内有且仅有一个零点.
x
y
0
x
y
0
反之不成立!
(5)定理的作用:判定零点的存在,并找出零点所在的区间。
(4) 若函数y= f(x)在区间(a, b)内有零点,一定能得出f(a)·f(b)<0的结论吗?
例1.函数f(x)=ex+x-2的零点所在的区间是( )
A.(-1,0) B.(0,1) C.(1,2) D.(2,3)
归纳: 判断函数零点所在区间的方法是将区间端点代入函数求出函数值,进行符号判断即可得出结论.
B
练习2.
1.函数f(x)=ln x+2x-6的零点所在的区间是( )
A.(1,2) B.(2,3) C.(3,4) D. (4,5)
B
2.方程lg x+x=0的根所在的区间可能是( )
A.(-∞,0) B.(0.1,1) C.(1,2) D.(2,4)
B
解:要使lg x有意义,必须x>0.
令f(x)=lg x+x,显然f(x)在定义域内为增函数,
又f(0.1)=-0.9<0,f(1)=1>0,故f(x)在区间(0.1,1)内有零点.
3.根据表中的数据,可以判定方程ex-x-2=0的一个根所在的区间为( )
A.(-1,0) B.(0,1) C.(1,2) D.(2,3)
C
ex-x-2 -0.63 -1 -0.28 3.39 15.09
练习2.
x -1 0 1 2 3
ex 0.37 1 2.72 7.39 20.09
x+2 1 2 3 4 5
解析 由上表可知f(1)=2.72-3<0,f(2)=7.39-4>0,
∴f(1)·f(2)<0,∴f(x)在区间(1,2)上存在零点.
练习3.
B
函数f(x)=lg x-1的零点个数是( )
A. 0 B. 1 C. 2 D.3
例2
归纳: 判断函数零点个数的方法
(1)直接求出函数的零点进行判断.
(2)结合函数的图象进行判断.
1.函数f(x)=1/x-2的零点的个数为( )
A.0 B.1 C.2 D.3
2.已知函数f(x)=
则函数g(x)=f(x)-1的零点个数为 ( )
A.0 B.1 C.2 D.3
B
C
4. 函数f(x)=lnx+2x-6的零点个数是( )
A. 0 B. 1 C. 2 D.3
练习3.
3.已知函数f(x)= 若函数g(x)=f(x)-m有3个零点,则实数m的取值范围是______.
[0,1)
例 求函数f(x)=lnx+2x-6的零点个数.
分析:函数f(x)=lnx+2x-6 (x>0) 是否有零点?有几个?
条件1:函数f(x)在(0,+∞)上的图象是连续不断的
条件2:f( )>0,f( )<0
解:∵f(x)在(0,+∞)上的图象是连续不断的
∴函数f(x)在区间(1,3)内有零点
又∵函数f(x)在定义域(0,+∞)上单调递增
∴函数f(x)=lnx+2x-6(x>0)只有一个零点
又∵f(1)=-4<0,f(3)=ln3>0
∴f(1)·f(3)<0
函数y=lnx+2x-6零点的个数
数形结合
两个函数 的交点的个数
方程lnx=6-2x 根的个数
两个函数 的交点的个数
函数y=lnx+2x-6与x轴交点的个数
方程lnx+2x-6=0根的个数
x
y
0
1
6
3
归纳:确定函数零点个数的主要方法
1.解相应的方程,确定方程的实根个数.
2.能够将函数的零点问题转化为两个函数图象的交点问题,
数形结合求解.
1.方程ex +x -2=0的根的个数是( )
A.0 B.1 C.2 D.3
练习4
x
y
0
1
2
2
解析:作出函数g(x)= ex和h(x)=2-x的图象,
B
2. 已知函数f(x)=2x+x,g(x)=log2x+x,h(x)=x3+x的零点依次为a,b,c,则a,b,c的大小关系为( )
A.a<b<c B.a<c<b
C.a>b>c D.c>a>b
解: f(x)=2x+x的零点a为函数y=2x与y=-x图象的交点的横坐标,由图象可知a<0,g(x)=log2x+x的零点b为函数y=log2x与y=-x图象的交点的横坐标,由图象知b>0,令h(x)=0,得c=0.故选B.
三.课堂小结
一个关系:函数零点与方程根的关系
方程 的根
函数 的零点
函数 的图象与x轴交点的横坐标
1.
2.一个定理:零点的存在性定理
函数与方程
数形结合
四.作业
五.课后思考:
1.若方程log3 x+x-3=0的解所在的区间为(k,k+1),
则整数k的值为______.
2
1.第155页第2题
2.已知函数 和g(x)= 2x ,
设h(x)= f(x) - g(x) ,试通过图象确定h(x) 的零点个数?
f(x)=
在数学的发展史上,方程的求解一直都是数学发展、数学教育和数学研究的最核心环节之一.
我国古代数学家已比较系统地解决了部分方程求解的问题. 约公元50年—100年编成的《九章算术》,就给出了求一次方程、二次方程和正系数三次方程根的具体方法…
前面我们学习了函数的知识,那么函数和方程有什么关系呢?面对一个实际问题,我们又该选择什么函数模型来加以解决呢?这正是函数的应用(二)所要解决的问题!让我们先从下面的问题开始吧!
4.5 函数的应用(二)
4.5.1函数的零点与方程的解
问题1:下列方程有实数根吗?
一.生成概念
(1) x2-2x-3=0
(2) x2-2x+1=0
(3) x2-2x+3=0
追问 还有其它方法判断方程
x2-2x-3=0有实数根吗?
f(x)=x2-2x-3
方程
x2-2x+1=0
x2-2x+3=0
y= x2-2x-3
y= x2-2x+1
函数
函
数
的
图
象
方程的实数解
x1=-1,x2=3
x1=x2=1
无实数根
函数的图象
与x轴的交点
(-1,0)、(3,0)
(1,0)
无交点
x2-2x-3=0
x
y
0
-1
3
2
1
1
2
.
.
x
y
0
-1
3
2
1
1
2
3
.
y
x
0
2
1
1
2
y= x2-2x+3
方程的实数解就是对应函数图象与x轴交点的横坐标。
结 论:
思考:这个结论对一般的二次函数和方程成立吗?
判别式 >0 0 <0
y=ax2+bx+c 的图象
ax2+bx+c=0 的根
x
y
x1
x2
0
x
y
0
x
y
0
函数的图象
与 x 轴的交点
两个交点(x1,0) , (x2,0)
无交点
两个相等的实数根x1 = x2
无实数根
两个不相等的实数根x1 、x2
结论:一元二次方程的根就是相应的二次函数图象与X轴交点的横坐标。
一元二次方程ax2+bx+c=0(a>0)的根与二次函数
y= ax2+bx+c(a>0)的图象:
x1=x2
一个交点(x1,0)
1.函数的零点
对于函数y=f(x), 使f(x)=0的实数x
叫做函数y=f(x)的零点.
注意:(1) 零点是一个实数
零点是一个点吗
推广到更一般的情况:
归纳:
1.代数法:函数零点就是相应方程的实数根,可解相应方程求函数的零点.
2.几何法:作出函数y=f(x)的图象,确定图象与x轴的交点的横坐标,求函数的零点.
1. 函数f(x)=(x - 1)(x +2)的零点是( )
A.(1,0),(- 2,0), B. 1, - 2
C.(0,1),(0, - 2), D. - 1, 2
练习1
2. (1)f(x)= 2x-1的零点是________.
B
0
(2)函数f(x)=
的零点是________.
观察1 函数f(x)= x2-2x-3在其零点附近函数值的变化情况.
(1).f(-2)f(1)__0 (>或<),
<
(2).f(2)f(4)__0 (>或<),
<
二.发现定理
f(x)=x2-2x-3
f(x)在开区间(-2,1)内___ (有/无)零点
f(x)在开区间(2,4)内___ (有/无)零点
有
有
观察2 函数y=f(x)在其零点附近的函数值的变化情况.
(1)f(a)f(b)__0(>或<),
<
f(x)在开区间(a,b)内___ (有/无)零点;
<
<
有
(2)f(b)f(c)__0(>或<),
f(x)在开区间(b,c)内___ (有/无)零点;
有
(3)f(c)f(d)__0(>或<),
f(x)在开区间(c,d)内___ (有/无)零点.
有
问题2 你发现了什么?
如果函数y=f(x)在区间[a,b]上
有f(a)f(b)﹤0,那么函 数y=f(x)在(a,b)内有零点,即存在c∈ (a,b),使得f(c)=0,这个c也就是方程f(x)=0的根.
的图象是连续不断的一条曲线,并且
猜想:
2.函数零点存在性定理
观察函数图象(如右图)并思考:
O
-1
1
-1
1
函数f(x)满足了f(-1)f(1)<0,它在区间
(-1,1)上有没有零点?
至少有一个,
可以有多个.
注意: (1)两个前提条件缺一不可.
(2)“有零点”是指有几个零点呢?
只有一个吗?
(3)再加上什么条件就“有且仅有一个零点”呢?
x
y
0
如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且f(a)f(b)﹤0,并且是单调函数,那么函 数y=f(x)在(a,b)内有且仅有一个零点.
x
y
0
x
y
0
反之不成立!
(5)定理的作用:判定零点的存在,并找出零点所在的区间。
(4) 若函数y= f(x)在区间(a, b)内有零点,一定能得出f(a)·f(b)<0的结论吗?
例1.函数f(x)=ex+x-2的零点所在的区间是( )
A.(-1,0) B.(0,1) C.(1,2) D.(2,3)
归纳: 判断函数零点所在区间的方法是将区间端点代入函数求出函数值,进行符号判断即可得出结论.
B
练习2.
1.函数f(x)=ln x+2x-6的零点所在的区间是( )
A.(1,2) B.(2,3) C.(3,4) D. (4,5)
B
2.方程lg x+x=0的根所在的区间可能是( )
A.(-∞,0) B.(0.1,1) C.(1,2) D.(2,4)
B
解:要使lg x有意义,必须x>0.
令f(x)=lg x+x,显然f(x)在定义域内为增函数,
又f(0.1)=-0.9<0,f(1)=1>0,故f(x)在区间(0.1,1)内有零点.
3.根据表中的数据,可以判定方程ex-x-2=0的一个根所在的区间为( )
A.(-1,0) B.(0,1) C.(1,2) D.(2,3)
C
ex-x-2 -0.63 -1 -0.28 3.39 15.09
练习2.
x -1 0 1 2 3
ex 0.37 1 2.72 7.39 20.09
x+2 1 2 3 4 5
解析 由上表可知f(1)=2.72-3<0,f(2)=7.39-4>0,
∴f(1)·f(2)<0,∴f(x)在区间(1,2)上存在零点.
练习3.
B
函数f(x)=lg x-1的零点个数是( )
A. 0 B. 1 C. 2 D.3
例2
归纳: 判断函数零点个数的方法
(1)直接求出函数的零点进行判断.
(2)结合函数的图象进行判断.
1.函数f(x)=1/x-2的零点的个数为( )
A.0 B.1 C.2 D.3
2.已知函数f(x)=
则函数g(x)=f(x)-1的零点个数为 ( )
A.0 B.1 C.2 D.3
B
C
4. 函数f(x)=lnx+2x-6的零点个数是( )
A. 0 B. 1 C. 2 D.3
练习3.
3.已知函数f(x)= 若函数g(x)=f(x)-m有3个零点,则实数m的取值范围是______.
[0,1)
例 求函数f(x)=lnx+2x-6的零点个数.
分析:函数f(x)=lnx+2x-6 (x>0) 是否有零点?有几个?
条件1:函数f(x)在(0,+∞)上的图象是连续不断的
条件2:f( )>0,f( )<0
解:∵f(x)在(0,+∞)上的图象是连续不断的
∴函数f(x)在区间(1,3)内有零点
又∵函数f(x)在定义域(0,+∞)上单调递增
∴函数f(x)=lnx+2x-6(x>0)只有一个零点
又∵f(1)=-4<0,f(3)=ln3>0
∴f(1)·f(3)<0
函数y=lnx+2x-6零点的个数
数形结合
两个函数 的交点的个数
方程lnx=6-2x 根的个数
两个函数 的交点的个数
函数y=lnx+2x-6与x轴交点的个数
方程lnx+2x-6=0根的个数
x
y
0
1
6
3
归纳:确定函数零点个数的主要方法
1.解相应的方程,确定方程的实根个数.
2.能够将函数的零点问题转化为两个函数图象的交点问题,
数形结合求解.
1.方程ex +x -2=0的根的个数是( )
A.0 B.1 C.2 D.3
练习4
x
y
0
1
2
2
解析:作出函数g(x)= ex和h(x)=2-x的图象,
B
2. 已知函数f(x)=2x+x,g(x)=log2x+x,h(x)=x3+x的零点依次为a,b,c,则a,b,c的大小关系为( )
A.a<b<c B.a<c<b
C.a>b>c D.c>a>b
解: f(x)=2x+x的零点a为函数y=2x与y=-x图象的交点的横坐标,由图象可知a<0,g(x)=log2x+x的零点b为函数y=log2x与y=-x图象的交点的横坐标,由图象知b>0,令h(x)=0,得c=0.故选B.
三.课堂小结
一个关系:函数零点与方程根的关系
方程 的根
函数 的零点
函数 的图象与x轴交点的横坐标
1.
2.一个定理:零点的存在性定理
函数与方程
数形结合
四.作业
五.课后思考:
1.若方程log3 x+x-3=0的解所在的区间为(k,k+1),
则整数k的值为______.
2
1.第155页第2题
2.已知函数 和g(x)= 2x ,
设h(x)= f(x) - g(x) ,试通过图象确定h(x) 的零点个数?
f(x)=
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
