2021-2022学年数学人教A版(2019)选择性必修第一册2.3.4两平行直线间的距离公式课件(共24张PPT)
文档属性
| 名称 | 2021-2022学年数学人教A版(2019)选择性必修第一册2.3.4两平行直线间的距离公式课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-27 00:00:00 | ||
图片预览








文档简介
(共24张PPT)
2.3.4两平行直线间的距离公式
1.概念的形成
1.1创设情境,引发思考
问题1:立定跳远测量的什么距离?
A.两平行线的距离
B.点到直线的距离
C.点到点的距离
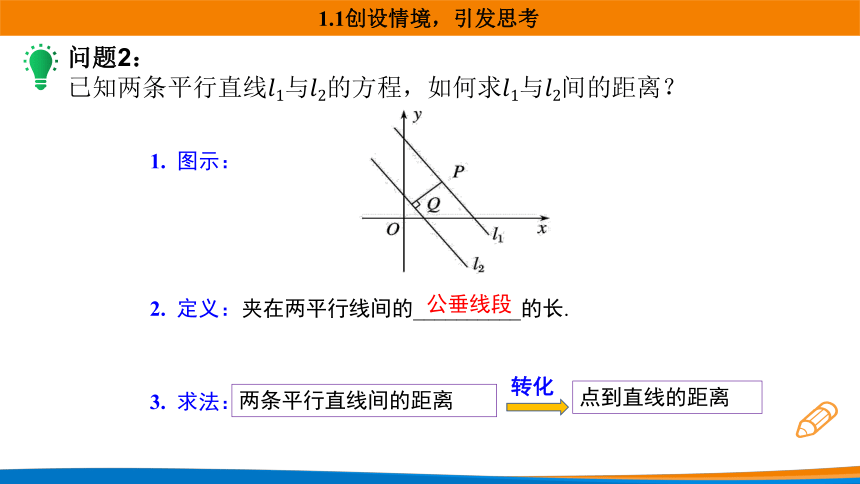
2. 定义:夹在两平行线间的__________的长.
公垂线段
1. 图示:
3. 求法:
1.1创设情境,引发思考
问题2:
已知两条平行直线的方程,如何求间的距离?
两条平行直线间的距离
点到直线的距离
转化
1.2探究典例,形成概念
活动:已知两条平行直线,
求间的距离.
解:在直线2x - 7y-8=0上任取一点,如P(4,0)
则两平行线的距离就是点P(4,0)到直线6x-21y-1=0的距离.
因此,d=
问题3:如何取点,可使计算简单?
P
解 : 在直线l1: 上任取一点 ,点
到直线l2: 距离,就是这两条平行线间的距离即
因为点 在直线 上,所以 ,
即 ,因此
1.2探究典例,形成概念
问题4:
两条平行线=0与=0间的距离为_______
1.2探究典例,形成概念
验证:已知两条平行直线,
求间的距离.
解:
问题5:
两条平行直线间的距离公式写成时 对两条直线应有什么要求?
(1)把直线方程化为直线的一般式方程;
(2)两条直线方程中x,y的系数必须分别相等;
1.3具体感知,理性分析
活动:自主举例的接龙活动.
【活动要求】
第一组用一般式写出两条平行直线方程并求出两平行直线间的距离.
第二组用斜截式写出两条平行直线方程并求出两平行直线间的距离;
问题6:
一般地,两条平行直线 间的距离:
与 , 公式结构有什么关联?
1.3具体感知,理性分析
2.初步应用,理解概念
追问:两条直线是平行的吗?
斜率相等,截距不等,所以两直线平行.
例1 (1)已知两直线l1:3x+5y+1=0和l2:6x+10y+5=0,则l1与l2间的距离为 .
(2)直线3x+y-3=0和直线6x+my-1=0平行,则它们之间的距离为 .
例2 □ABCD的四条边所在直线的方程分别是
求□ABCD的面积.
追问1:如何求 CD ?
CD 的长
C、D 的坐标
联立方程求交点
2.初步应用,理解概念
解得交点C的坐标为 .
2.初步应用,理解概念
例2 □ABCD的四条边所在直线的方程分别是
求□ABCD的面积.
解得交点D的坐标为 .
2.初步应用,理解概念
例2 □ABCD的四条边所在直线的方程分别是
求□ABCD的面积.
D的坐标为 .
由交点C的坐标为 ,
2.初步应用,理解概念
例2 □ABCD的四条边所在直线的方程分别是
求□ABCD的面积.
追问2:如何求高 ?
点到直线的距离
平行直线间的距离
求点
2.初步应用,理解概念
例2 □ABCD的四条边所在直线的方程分别是
求□ABCD的面积.
2.初步应用,理解概念
例2 □ABCD的四条边所在直线的方程分别是
求□ABCD的面积.
(2)已知直线l1:3x-2y-1=0和l2:3x-2y-13=0,直线l与l1,l2的距离分别是d1,d2,若d1∶d2=2∶1,求直线l的方程.
2.初步应用,理解概念
例3(1)已知直线l与两直线l1:y=2x+3和l2:y=2x-1间的距离相等,求直线l的方程.
待定系数法
3.归纳小结
4.课外作业
再会!
1.若直线l1:x+my+6=0与l2:(m-2)x+3y+2m=0互相平行,则m的值为 ,它们之间的距离为 .
解析:由m(m-2)-3=0,解得m=3或-1.经过验证,m=3时两条直线重合,舍去.∴m=-1.
2.已知直线l1,l2是分别经过A(1,1),B(0,-1)两点的两条平行直线,当l1,l2间的距离最大时,直线l1的方程是 .
当两条平行直线与A,B两点的连线垂直时,两条平行直线间的距离最大.
因为A(1,1),B(0,-1).所以kAB==2,所以两条平行直线的斜率为-,
所以直线l1的方程为y-1=-(x-1),即x+2y-3=0.
课外作业答案
3.直线l1过点A(0,1),l2过点B(5,0),如果l1∥l2,且l1与l2间的距离为5,求l1,l2的方程.
课外作业答案
课外作业答案
金题典例
课外作业答案
主色
辅色
文字用色
辅色
通用色:
图标:
2.3.4两平行直线间的距离公式
1.概念的形成
1.1创设情境,引发思考
问题1:立定跳远测量的什么距离?
A.两平行线的距离
B.点到直线的距离
C.点到点的距离
2. 定义:夹在两平行线间的__________的长.
公垂线段
1. 图示:
3. 求法:
1.1创设情境,引发思考
问题2:
已知两条平行直线的方程,如何求间的距离?
两条平行直线间的距离
点到直线的距离
转化
1.2探究典例,形成概念
活动:已知两条平行直线,
求间的距离.
解:在直线2x - 7y-8=0上任取一点,如P(4,0)
则两平行线的距离就是点P(4,0)到直线6x-21y-1=0的距离.
因此,d=
问题3:如何取点,可使计算简单?
P
解 : 在直线l1: 上任取一点 ,点
到直线l2: 距离,就是这两条平行线间的距离即
因为点 在直线 上,所以 ,
即 ,因此
1.2探究典例,形成概念
问题4:
两条平行线=0与=0间的距离为_______
1.2探究典例,形成概念
验证:已知两条平行直线,
求间的距离.
解:
问题5:
两条平行直线间的距离公式写成时 对两条直线应有什么要求?
(1)把直线方程化为直线的一般式方程;
(2)两条直线方程中x,y的系数必须分别相等;
1.3具体感知,理性分析
活动:自主举例的接龙活动.
【活动要求】
第一组用一般式写出两条平行直线方程并求出两平行直线间的距离.
第二组用斜截式写出两条平行直线方程并求出两平行直线间的距离;
问题6:
一般地,两条平行直线 间的距离:
与 , 公式结构有什么关联?
1.3具体感知,理性分析
2.初步应用,理解概念
追问:两条直线是平行的吗?
斜率相等,截距不等,所以两直线平行.
例1 (1)已知两直线l1:3x+5y+1=0和l2:6x+10y+5=0,则l1与l2间的距离为 .
(2)直线3x+y-3=0和直线6x+my-1=0平行,则它们之间的距离为 .
例2 □ABCD的四条边所在直线的方程分别是
求□ABCD的面积.
追问1:如何求 CD ?
CD 的长
C、D 的坐标
联立方程求交点
2.初步应用,理解概念
解得交点C的坐标为 .
2.初步应用,理解概念
例2 □ABCD的四条边所在直线的方程分别是
求□ABCD的面积.
解得交点D的坐标为 .
2.初步应用,理解概念
例2 □ABCD的四条边所在直线的方程分别是
求□ABCD的面积.
D的坐标为 .
由交点C的坐标为 ,
2.初步应用,理解概念
例2 □ABCD的四条边所在直线的方程分别是
求□ABCD的面积.
追问2:如何求高 ?
点到直线的距离
平行直线间的距离
求点
2.初步应用,理解概念
例2 □ABCD的四条边所在直线的方程分别是
求□ABCD的面积.
2.初步应用,理解概念
例2 □ABCD的四条边所在直线的方程分别是
求□ABCD的面积.
(2)已知直线l1:3x-2y-1=0和l2:3x-2y-13=0,直线l与l1,l2的距离分别是d1,d2,若d1∶d2=2∶1,求直线l的方程.
2.初步应用,理解概念
例3(1)已知直线l与两直线l1:y=2x+3和l2:y=2x-1间的距离相等,求直线l的方程.
待定系数法
3.归纳小结
4.课外作业
再会!
1.若直线l1:x+my+6=0与l2:(m-2)x+3y+2m=0互相平行,则m的值为 ,它们之间的距离为 .
解析:由m(m-2)-3=0,解得m=3或-1.经过验证,m=3时两条直线重合,舍去.∴m=-1.
2.已知直线l1,l2是分别经过A(1,1),B(0,-1)两点的两条平行直线,当l1,l2间的距离最大时,直线l1的方程是 .
当两条平行直线与A,B两点的连线垂直时,两条平行直线间的距离最大.
因为A(1,1),B(0,-1).所以kAB==2,所以两条平行直线的斜率为-,
所以直线l1的方程为y-1=-(x-1),即x+2y-3=0.
课外作业答案
3.直线l1过点A(0,1),l2过点B(5,0),如果l1∥l2,且l1与l2间的距离为5,求l1,l2的方程.
课外作业答案
课外作业答案
金题典例
课外作业答案
主色
辅色
文字用色
辅色
通用色:
图标:
