高一上学期物理人教版(2019)必修第一册第二章 匀变速直线运动的研究 期末质量检测卷(word版含答案)
文档属性
| 名称 | 高一上学期物理人教版(2019)必修第一册第二章 匀变速直线运动的研究 期末质量检测卷(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 366.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-11-27 22:21:41 | ||
图片预览


文档简介
第二章 匀变速直线运动的研究 期末质量检测卷
一、单选题
1.某质点的位移随时间变化的关系式为x=4t+2t2,x与t的单位分别是m和s,则质点的初速度和加速度分别是( )
A.4m/s和2 m/s2 B.0和4m/s2
C.4m/s 和4 m/s2 D.4m/s和0
2.一质点做匀加速直线运动时,速度变化时发生位移,紧接着速度变化同样的时发生位移,则质点的加速度为( )
A. B. C. D.
3.从某一高度相隔1s先后自由释放两个相同的小球甲和乙,不计空气阻力,它们在空中任一时刻( )
A.甲、乙两球距离始终保持不变,甲、乙两球速度之差保持不变
B.甲、乙两球距离越来越大,甲、乙两球速度之差也越来越大
C.甲、乙两球距离越来大,甲、乙两球速度之差保持不变
D.甲、乙两球距离越来越小,甲、乙两球速度之差也越来越小
4.如图所示,物体从O点由静止开始做匀加速直线运动,途经A、B、C三点,其中,。若物体通过和这两段位移的时间相等,则O、A两点之间的距离等于( )
A. B. C. D.
5.一辆汽车由静止开始做匀变速直线运动,刚运动了8 s,由于前方突然有巨石滚在路中央,所以又紧急刹车,经4 s 停在巨石前。则关于汽车的运动情况,下列说法正确的是( )
A.加速、减速中的加速度大小之比a1∶a2=1∶2
B.加速、减速中的位移之比x1∶x2=1∶1
C.加速、减速中的平均速度之比v1∶v2=2∶1
D.加速、减速中的加速度大小之比a1∶a2=2∶1
6.汽车从A点由静止开始沿直线AC做匀加速直线运动,第4s末通过C点时关闭发动机,做匀减速直线运动,再经过6s到达B点时停止。已知AB长30m,则下列说法错误的是( )
A.通过C点时的速度大小为3m/s
B.通过C点时的速度大小为6m/s
C.通过AC段的位移为12m
D.汽车在AC、CB两段的平均速度大小相同
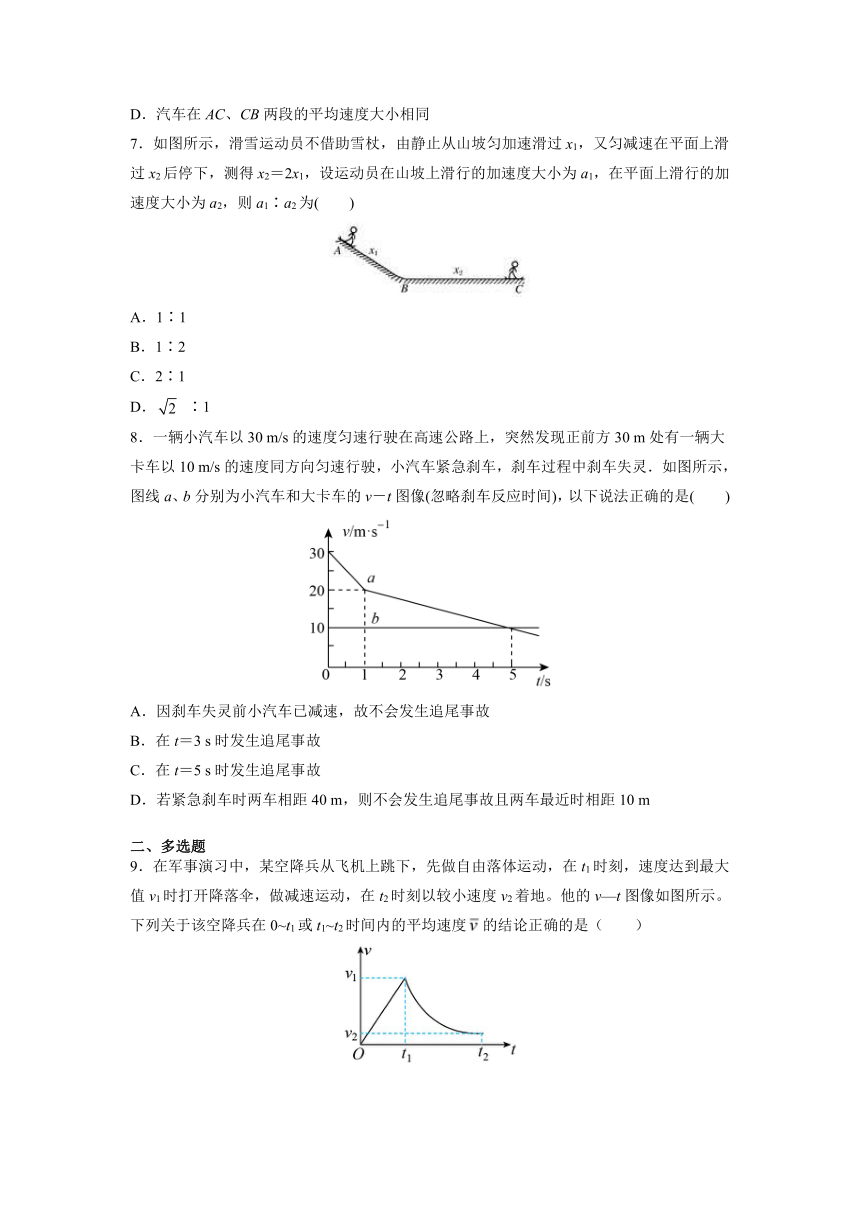
7.如图所示,滑雪运动员不借助雪杖,由静止从山坡匀加速滑过x1,又匀减速在平面上滑过x2后停下,测得x2=2x1,设运动员在山坡上滑行的加速度大小为a1,在平面上滑行的加速度大小为a2,则a1∶a2为( )
A.1∶1
B.1∶2
C.2∶1
D. ∶1
8.一辆小汽车以30 m/s的速度匀速行驶在高速公路上,突然发现正前方30 m处有一辆大卡车以10 m/s的速度同方向匀速行驶,小汽车紧急刹车,刹车过程中刹车失灵.如图所示,图线a、b分别为小汽车和大卡车的v-t图像(忽略刹车反应时间),以下说法正确的是( )
A.因刹车失灵前小汽车已减速,故不会发生追尾事故
B.在t=3 s时发生追尾事故
C.在t=5 s时发生追尾事故
D.若紧急刹车时两车相距40 m,则不会发生追尾事故且两车最近时相距10 m
二、多选题
9.在军事演习中,某空降兵从飞机上跳下,先做自由落体运动,在t1时刻,速度达到最大值v1时打开降落伞,做减速运动,在t2时刻以较小速度v2着地。他的v—t图像如图所示。下列关于该空降兵在0~t1或t1~t2时间内的平均速度的结论正确的是( )
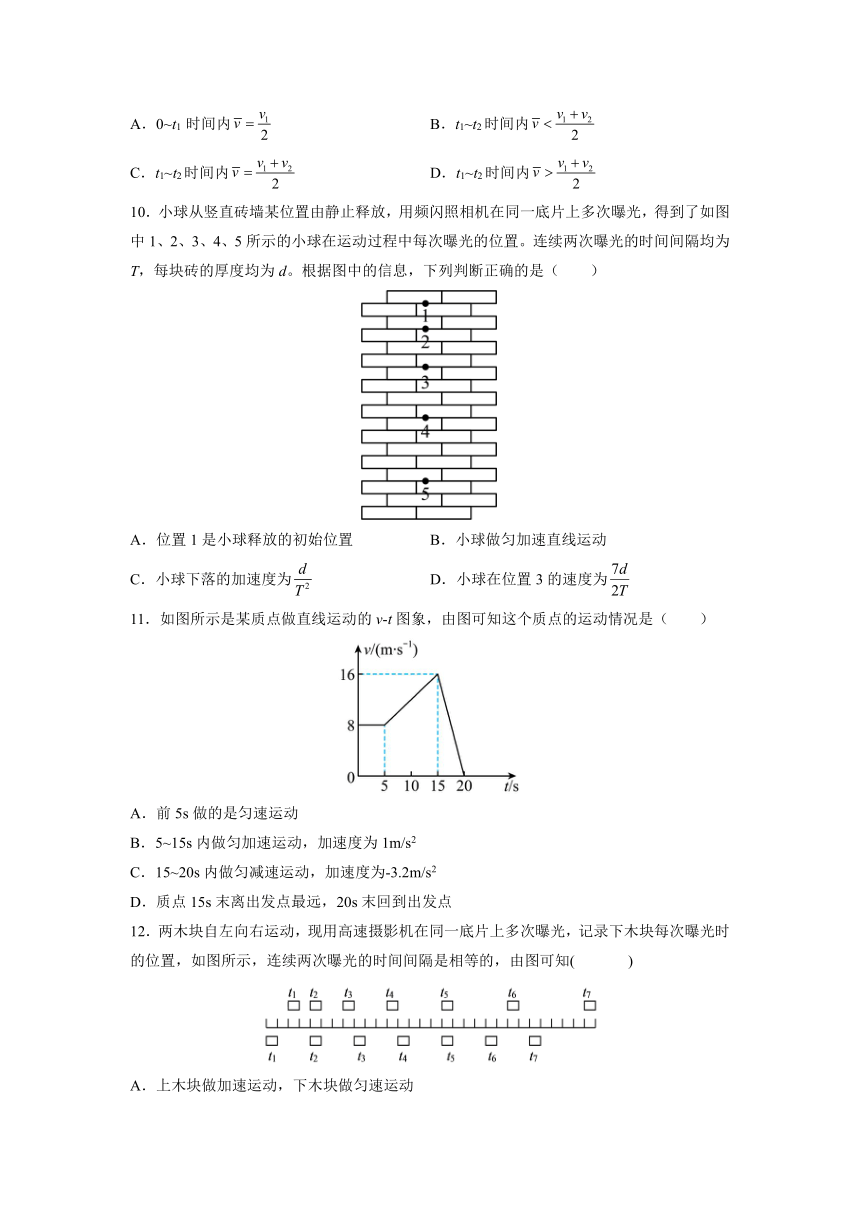
A.0~t1 时间内 B.t1~t2时间内
C.t1~t2时间内 D.t1~t2时间内
10.小球从竖直砖墙某位置由静止释放,用频闪照相机在同一底片上多次曝光,得到了如图中1、2、3、4、5所示的小球在运动过程中每次曝光的位置。连续两次曝光的时间间隔均为T,每块砖的厚度均为d。根据图中的信息,下列判断正确的是( )
A.位置1是小球释放的初始位置 B.小球做匀加速直线运动
C.小球下落的加速度为 D.小球在位置3的速度为
11.如图所示是某质点做直线运动的v-t图象,由图可知这个质点的运动情况是( )
A.前5s做的是匀速运动
B.5~15s内做匀加速运动,加速度为1m/s2
C.15~20s内做匀减速运动,加速度为-3.2m/s2
D.质点15s末离出发点最远,20s末回到出发点
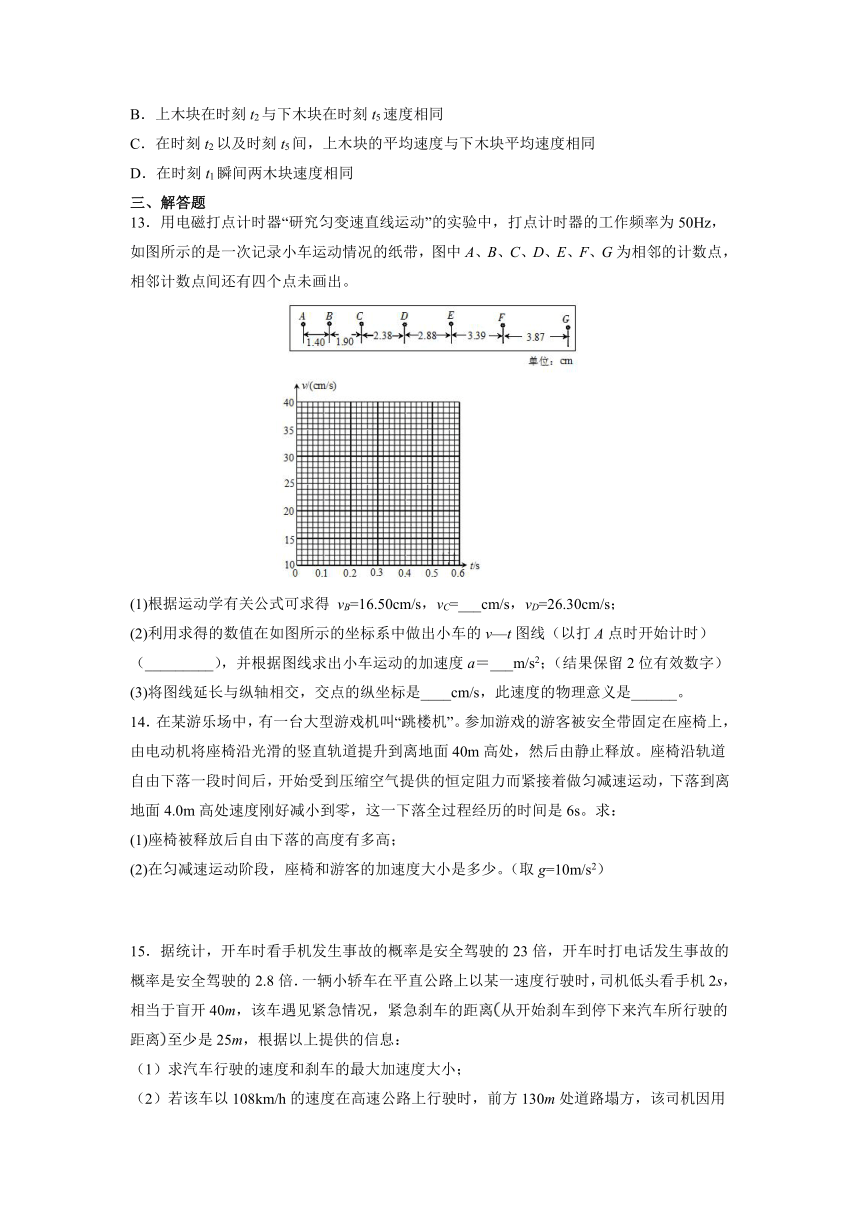
12.两木块自左向右运动,现用高速摄影机在同一底片上多次曝光,记录下木块每次曝光时的位置,如图所示,连续两次曝光的时间间隔是相等的,由图可知( )
A.上木块做加速运动,下木块做匀速运动
B.上木块在时刻t2与下木块在时刻t5速度相同
C.在时刻t2以及时刻t5间,上木块的平均速度与下木块平均速度相同
D.在时刻t1瞬间两木块速度相同
三、解答题
13.用电磁打点计时器“研究匀变速直线运动”的实验中,打点计时器的工作频率为50Hz,如图所示的是一次记录小车运动情况的纸带,图中A、B、C、D、E、F、G为相邻的计数点,相邻计数点间还有四个点未画出。
(1)根据运动学有关公式可求得 vB=16.50cm/s,vC=___cm/s,vD=26.30cm/s;
(2)利用求得的数值在如图所示的坐标系中做出小车的v—t图线(以打A点时开始计时)(_________),并根据图线求出小车运动的加速度a=___m/s2;(结果保留2位有效数字)
(3)将图线延长与纵轴相交,交点的纵坐标是____cm/s,此速度的物理意义是______。
14.在某游乐场中,有一台大型游戏机叫“跳楼机”。参加游戏的游客被安全带固定在座椅上,由电动机将座椅沿光滑的竖直轨道提升到离地面40m高处,然后由静止释放。座椅沿轨道自由下落一段时间后,开始受到压缩空气提供的恒定阻力而紧接着做匀减速运动,下落到离地面4.0m高处速度刚好减小到零,这一下落全过程经历的时间是6s。求:
(1)座椅被释放后自由下落的高度有多高;
(2)在匀减速运动阶段,座椅和游客的加速度大小是多少。(取g=10m/s2)
15.据统计,开车时看手机发生事故的概率是安全驾驶的23倍,开车时打电话发生事故的概率是安全驾驶的2.8倍.一辆小轿车在平直公路上以某一速度行驶时,司机低头看手机2s,相当于盲开40m,该车遇见紧急情况,紧急刹车的距离从开始刹车到停下来汽车所行驶的距离至少是25m,根据以上提供的信息:
(1)求汽车行驶的速度和刹车的最大加速度大小;
(2)若该车以108km/h的速度在高速公路上行驶时,前方130m处道路塌方,该司机因用手机微信抢红包2s后才发现危险,司机的反应时间为0.5s,刹车的加速度与(1)问中大小相等.试通过计算说明汽车是否会发生交通事故.
16.甲乙两辆汽车都从静止出发做加速直线运动,加速度方向一直不变。在第一段时间间隔内,两辆汽车的加速度大小不变,汽车乙的加速度大小是甲的两倍;在接下来的相同时间间隔内,汽车甲的加速度大小增加为原来的两倍,汽车乙的加速度大小减小为原来的一半。求甲乙两车各自在这两段时间间隔内走过的总路程之比。
参考答案
1.C
【解析】根据匀变速直线运动的位移与时间关系式,可得
解得
,
故选C。
2.A
【解析】发生所用的时间为
根据
得
解得
故选A。
3.C
【解析】设乙运动的时间为t,则甲运动时间为t+1,则两球的距离:
可知两球间的距离随时间增加越来越大;
两球速度之差为:
所以甲乙两球速度之差保持不变。
故选C。
4.C
【解析】设AB与BC的运动时间为T,由匀变速连续相邻相等时间内物体位移差公式
得
由中点时刻速度公式得
由
得
联立以上式子得
则
故选C。
5.A
【解析】AD.设汽车的最大速度为v,则加速运动的加速度大小为
减速运动的加速度大小为
则
a1:a2=t2:t1=4:8=1:2
故A正确,D错误。
BC.加速运动的平均速度大小
减速运动的平均速度大小
则平均速度之比
v1:v2=1:1
加速、减速中的位移之比
s1:s2=v1t1:v2t2=2:1
故BC错误。
故选A。
6.A
【解析】AB.设汽车通过C点时的速度为v,根据
x=t= t
得
xAC= ,xCB=
由
xAB=xAC+xCB=(t1+t2)=30m
得汽车通过C点时的速度为
v=6m/s
B正确,不符合题意;A错误,符合题意;
C.根据题意有
xAC==12m,xCB==18m
C正确,不符合题意;
D.由
==m/s=m/s=3m/s
知汽车在AC与CB两段的平均速度大小相同,D正确,不符合题意。
故选A。
7.C
【解析】由得 ,解得a1∶a2=s2∶s1=2∶1,故选C.
8.B
【解析】ABC.根据速度—时间图线与时间轴所围“面积”大小等于位移大小,由题图知,t=3 s时大卡车的位移为
xb=vbt=10×3 m=30 m
小汽车的位移为
xa=×(30+20)×1 m+×(20+15)×2 m=60 m
则
xa-xb=30 m
所以在t=3 s时发生追尾事故,故B正确,AC错误;
D.由v-t图线可知在t=5 s时两车速度相等,小汽车相对于大卡车的位移
Δx=×(20+10)×1 m+×10×4 m=35 m<40 m
则不会发生追尾事故且两车最近时相距
Δs=x0-Δx=5 m
故D错误。
故选B。
9.AB
【解析】A.空降兵在0~t1时间内做自由落体运动,为匀变速直线运动,则有
故A正确;
BCD.在t1~t2时间内做加速度不断减小的减速运动,位移等于速度时间图线与时间轴包围的面积,此面积比虚线(直线,即为做匀减速直线运动的图线)面积小,如图所示
则有
故B正确,CD错误。
故选AB。
10.BCD
【解析】A.根据初速度为零的匀变速直线运动规律,连续相等时间位移之比为1:3:5…,A错误;
B.因为连续相等时间位移之差相等,所以小球做匀加速直线运动。B正确;
C.根据匀变速直线运动的规律得
解得
C正确;
D.小球在位置3的速度为
D正确。
故选BCD。
11.AC
【解析】A.由图象可知,前5s做的是匀速运动,A正确;
B.5~15s内做匀加速运动,加速度
B错误:
C.15~20s做匀减速运动,其加速度
C正确;
D.质点在20s末离出发点最远,质点一直做的是方向不变的直线运动,D错误。
故选AC
12.AC
【解析】A. 上面木块在相等时间内的位移之差是一恒量,知上木块做加速运动,下木块在相等时间内的位移大小相等,做匀速直线运动,故A正确;
B.根据某段时间内的平均速度等于中间时刻的瞬时速度,设每一小格为d,则上木块在时刻t2的速度,下木块的速度,故B错误;
C.在时刻t2以及时刻t5间,上下木块运动的位移大小相等,时间相等,则平均速度相等,故C正确;
D.根据△x=aT2得,上面木块的加速度,则在时刻t1瞬间上面木块的瞬时速度
与下木块的速度不等,故D错误.
故选AC。
13.21.40 0.49 11.60 开始计时时小车的速度(即表示小车在A点的瞬时速度)
【解析】(1)[1]电磁打点计时器频率是50Hz时,它们每隔0.02s打一次点,根据题意可知:每相邻两个计数点间还有4个点没有画出,因此计数点之间的时间间隔为
根据匀变速直线运动中时间中点的速度等于该过程中的平均速度,因此有
(2)[2]描点作图,用平滑曲线连接,如图所示
[3]速度图象中斜率即加速度,所以
(3)[4]将图线延长与纵轴相交,交点的纵坐标是11.60cm/s;
[5]此速度的物理意义是:开始计时时小车的速度(即表示小车在A点的瞬时速度)。
14.(1)h=7.2m;(2)a=2.5m/s2
【解析】(1)画出v-t图,如图所示
由图象知,“面积”
得
根据自由落体运动规律,座椅被释放后自由下落的高度
(2)物体做匀减速运动的位移
s′=(36-7.2)m=28.8m
由公式
v2=2as′
可知在匀减速运动阶段,游客的加速度大小
15.(1)8m/s2(2)会发生交通事故
【分析】
(1)根据司机低头看手机2s,相当于盲开40m,由位移时间关系求得汽车的行驶速度,由速度位移关系即可求解汽车刹车的最大加速度;
(2)汽车盲开和反应时间内都在做匀速直线运动,据速度位移关系求得匀速运动位移,刹车后做匀减速运动,由位移速度关系求得匀减速运动位移,再比较总位移与100m的大小确定是否发生交通事故.
【解析】(1)汽车运动的速度为
汽车刹车的最大加速度为a,则
(2)108km/h=30m/s
司机看手机时,汽车发生的位移为
x1=v2t=30×2=60m
反应时间内发生的位移的大小为
x2=v2△t=30×0.5=15m
刹车后汽车发生的位移
所以汽车前进的距离为x=x1+x2+x3=60+15+36=131.25m>130m
所以会发生交通事故.
【点睛】
掌握匀速直线运动和匀变速直线运动的位移时间关系,知道司机低头开的时间和反应时间内汽车做匀速直线运动,刹车后做匀减速直线运动,这是解决本题的关键.
16.
【解析】设甲开始的加速度为a,两段时间间隔都为t,则甲在两段时间内的总路程为:
乙在两段时间内的总路程为:
由上两式得
一、单选题
1.某质点的位移随时间变化的关系式为x=4t+2t2,x与t的单位分别是m和s,则质点的初速度和加速度分别是( )
A.4m/s和2 m/s2 B.0和4m/s2
C.4m/s 和4 m/s2 D.4m/s和0
2.一质点做匀加速直线运动时,速度变化时发生位移,紧接着速度变化同样的时发生位移,则质点的加速度为( )
A. B. C. D.
3.从某一高度相隔1s先后自由释放两个相同的小球甲和乙,不计空气阻力,它们在空中任一时刻( )
A.甲、乙两球距离始终保持不变,甲、乙两球速度之差保持不变
B.甲、乙两球距离越来越大,甲、乙两球速度之差也越来越大
C.甲、乙两球距离越来大,甲、乙两球速度之差保持不变
D.甲、乙两球距离越来越小,甲、乙两球速度之差也越来越小
4.如图所示,物体从O点由静止开始做匀加速直线运动,途经A、B、C三点,其中,。若物体通过和这两段位移的时间相等,则O、A两点之间的距离等于( )
A. B. C. D.
5.一辆汽车由静止开始做匀变速直线运动,刚运动了8 s,由于前方突然有巨石滚在路中央,所以又紧急刹车,经4 s 停在巨石前。则关于汽车的运动情况,下列说法正确的是( )
A.加速、减速中的加速度大小之比a1∶a2=1∶2
B.加速、减速中的位移之比x1∶x2=1∶1
C.加速、减速中的平均速度之比v1∶v2=2∶1
D.加速、减速中的加速度大小之比a1∶a2=2∶1
6.汽车从A点由静止开始沿直线AC做匀加速直线运动,第4s末通过C点时关闭发动机,做匀减速直线运动,再经过6s到达B点时停止。已知AB长30m,则下列说法错误的是( )
A.通过C点时的速度大小为3m/s
B.通过C点时的速度大小为6m/s
C.通过AC段的位移为12m
D.汽车在AC、CB两段的平均速度大小相同
7.如图所示,滑雪运动员不借助雪杖,由静止从山坡匀加速滑过x1,又匀减速在平面上滑过x2后停下,测得x2=2x1,设运动员在山坡上滑行的加速度大小为a1,在平面上滑行的加速度大小为a2,则a1∶a2为( )
A.1∶1
B.1∶2
C.2∶1
D. ∶1
8.一辆小汽车以30 m/s的速度匀速行驶在高速公路上,突然发现正前方30 m处有一辆大卡车以10 m/s的速度同方向匀速行驶,小汽车紧急刹车,刹车过程中刹车失灵.如图所示,图线a、b分别为小汽车和大卡车的v-t图像(忽略刹车反应时间),以下说法正确的是( )
A.因刹车失灵前小汽车已减速,故不会发生追尾事故
B.在t=3 s时发生追尾事故
C.在t=5 s时发生追尾事故
D.若紧急刹车时两车相距40 m,则不会发生追尾事故且两车最近时相距10 m
二、多选题
9.在军事演习中,某空降兵从飞机上跳下,先做自由落体运动,在t1时刻,速度达到最大值v1时打开降落伞,做减速运动,在t2时刻以较小速度v2着地。他的v—t图像如图所示。下列关于该空降兵在0~t1或t1~t2时间内的平均速度的结论正确的是( )
A.0~t1 时间内 B.t1~t2时间内
C.t1~t2时间内 D.t1~t2时间内
10.小球从竖直砖墙某位置由静止释放,用频闪照相机在同一底片上多次曝光,得到了如图中1、2、3、4、5所示的小球在运动过程中每次曝光的位置。连续两次曝光的时间间隔均为T,每块砖的厚度均为d。根据图中的信息,下列判断正确的是( )
A.位置1是小球释放的初始位置 B.小球做匀加速直线运动
C.小球下落的加速度为 D.小球在位置3的速度为
11.如图所示是某质点做直线运动的v-t图象,由图可知这个质点的运动情况是( )
A.前5s做的是匀速运动
B.5~15s内做匀加速运动,加速度为1m/s2
C.15~20s内做匀减速运动,加速度为-3.2m/s2
D.质点15s末离出发点最远,20s末回到出发点
12.两木块自左向右运动,现用高速摄影机在同一底片上多次曝光,记录下木块每次曝光时的位置,如图所示,连续两次曝光的时间间隔是相等的,由图可知( )
A.上木块做加速运动,下木块做匀速运动
B.上木块在时刻t2与下木块在时刻t5速度相同
C.在时刻t2以及时刻t5间,上木块的平均速度与下木块平均速度相同
D.在时刻t1瞬间两木块速度相同
三、解答题
13.用电磁打点计时器“研究匀变速直线运动”的实验中,打点计时器的工作频率为50Hz,如图所示的是一次记录小车运动情况的纸带,图中A、B、C、D、E、F、G为相邻的计数点,相邻计数点间还有四个点未画出。
(1)根据运动学有关公式可求得 vB=16.50cm/s,vC=___cm/s,vD=26.30cm/s;
(2)利用求得的数值在如图所示的坐标系中做出小车的v—t图线(以打A点时开始计时)(_________),并根据图线求出小车运动的加速度a=___m/s2;(结果保留2位有效数字)
(3)将图线延长与纵轴相交,交点的纵坐标是____cm/s,此速度的物理意义是______。
14.在某游乐场中,有一台大型游戏机叫“跳楼机”。参加游戏的游客被安全带固定在座椅上,由电动机将座椅沿光滑的竖直轨道提升到离地面40m高处,然后由静止释放。座椅沿轨道自由下落一段时间后,开始受到压缩空气提供的恒定阻力而紧接着做匀减速运动,下落到离地面4.0m高处速度刚好减小到零,这一下落全过程经历的时间是6s。求:
(1)座椅被释放后自由下落的高度有多高;
(2)在匀减速运动阶段,座椅和游客的加速度大小是多少。(取g=10m/s2)
15.据统计,开车时看手机发生事故的概率是安全驾驶的23倍,开车时打电话发生事故的概率是安全驾驶的2.8倍.一辆小轿车在平直公路上以某一速度行驶时,司机低头看手机2s,相当于盲开40m,该车遇见紧急情况,紧急刹车的距离从开始刹车到停下来汽车所行驶的距离至少是25m,根据以上提供的信息:
(1)求汽车行驶的速度和刹车的最大加速度大小;
(2)若该车以108km/h的速度在高速公路上行驶时,前方130m处道路塌方,该司机因用手机微信抢红包2s后才发现危险,司机的反应时间为0.5s,刹车的加速度与(1)问中大小相等.试通过计算说明汽车是否会发生交通事故.
16.甲乙两辆汽车都从静止出发做加速直线运动,加速度方向一直不变。在第一段时间间隔内,两辆汽车的加速度大小不变,汽车乙的加速度大小是甲的两倍;在接下来的相同时间间隔内,汽车甲的加速度大小增加为原来的两倍,汽车乙的加速度大小减小为原来的一半。求甲乙两车各自在这两段时间间隔内走过的总路程之比。
参考答案
1.C
【解析】根据匀变速直线运动的位移与时间关系式,可得
解得
,
故选C。
2.A
【解析】发生所用的时间为
根据
得
解得
故选A。
3.C
【解析】设乙运动的时间为t,则甲运动时间为t+1,则两球的距离:
可知两球间的距离随时间增加越来越大;
两球速度之差为:
所以甲乙两球速度之差保持不变。
故选C。
4.C
【解析】设AB与BC的运动时间为T,由匀变速连续相邻相等时间内物体位移差公式
得
由中点时刻速度公式得
由
得
联立以上式子得
则
故选C。
5.A
【解析】AD.设汽车的最大速度为v,则加速运动的加速度大小为
减速运动的加速度大小为
则
a1:a2=t2:t1=4:8=1:2
故A正确,D错误。
BC.加速运动的平均速度大小
减速运动的平均速度大小
则平均速度之比
v1:v2=1:1
加速、减速中的位移之比
s1:s2=v1t1:v2t2=2:1
故BC错误。
故选A。
6.A
【解析】AB.设汽车通过C点时的速度为v,根据
x=t= t
得
xAC= ,xCB=
由
xAB=xAC+xCB=(t1+t2)=30m
得汽车通过C点时的速度为
v=6m/s
B正确,不符合题意;A错误,符合题意;
C.根据题意有
xAC==12m,xCB==18m
C正确,不符合题意;
D.由
==m/s=m/s=3m/s
知汽车在AC与CB两段的平均速度大小相同,D正确,不符合题意。
故选A。
7.C
【解析】由得 ,解得a1∶a2=s2∶s1=2∶1,故选C.
8.B
【解析】ABC.根据速度—时间图线与时间轴所围“面积”大小等于位移大小,由题图知,t=3 s时大卡车的位移为
xb=vbt=10×3 m=30 m
小汽车的位移为
xa=×(30+20)×1 m+×(20+15)×2 m=60 m
则
xa-xb=30 m
所以在t=3 s时发生追尾事故,故B正确,AC错误;
D.由v-t图线可知在t=5 s时两车速度相等,小汽车相对于大卡车的位移
Δx=×(20+10)×1 m+×10×4 m=35 m<40 m
则不会发生追尾事故且两车最近时相距
Δs=x0-Δx=5 m
故D错误。
故选B。
9.AB
【解析】A.空降兵在0~t1时间内做自由落体运动,为匀变速直线运动,则有
故A正确;
BCD.在t1~t2时间内做加速度不断减小的减速运动,位移等于速度时间图线与时间轴包围的面积,此面积比虚线(直线,即为做匀减速直线运动的图线)面积小,如图所示
则有
故B正确,CD错误。
故选AB。
10.BCD
【解析】A.根据初速度为零的匀变速直线运动规律,连续相等时间位移之比为1:3:5…,A错误;
B.因为连续相等时间位移之差相等,所以小球做匀加速直线运动。B正确;
C.根据匀变速直线运动的规律得
解得
C正确;
D.小球在位置3的速度为
D正确。
故选BCD。
11.AC
【解析】A.由图象可知,前5s做的是匀速运动,A正确;
B.5~15s内做匀加速运动,加速度
B错误:
C.15~20s做匀减速运动,其加速度
C正确;
D.质点在20s末离出发点最远,质点一直做的是方向不变的直线运动,D错误。
故选AC
12.AC
【解析】A. 上面木块在相等时间内的位移之差是一恒量,知上木块做加速运动,下木块在相等时间内的位移大小相等,做匀速直线运动,故A正确;
B.根据某段时间内的平均速度等于中间时刻的瞬时速度,设每一小格为d,则上木块在时刻t2的速度,下木块的速度,故B错误;
C.在时刻t2以及时刻t5间,上下木块运动的位移大小相等,时间相等,则平均速度相等,故C正确;
D.根据△x=aT2得,上面木块的加速度,则在时刻t1瞬间上面木块的瞬时速度
与下木块的速度不等,故D错误.
故选AC。
13.21.40 0.49 11.60 开始计时时小车的速度(即表示小车在A点的瞬时速度)
【解析】(1)[1]电磁打点计时器频率是50Hz时,它们每隔0.02s打一次点,根据题意可知:每相邻两个计数点间还有4个点没有画出,因此计数点之间的时间间隔为
根据匀变速直线运动中时间中点的速度等于该过程中的平均速度,因此有
(2)[2]描点作图,用平滑曲线连接,如图所示
[3]速度图象中斜率即加速度,所以
(3)[4]将图线延长与纵轴相交,交点的纵坐标是11.60cm/s;
[5]此速度的物理意义是:开始计时时小车的速度(即表示小车在A点的瞬时速度)。
14.(1)h=7.2m;(2)a=2.5m/s2
【解析】(1)画出v-t图,如图所示
由图象知,“面积”
得
根据自由落体运动规律,座椅被释放后自由下落的高度
(2)物体做匀减速运动的位移
s′=(36-7.2)m=28.8m
由公式
v2=2as′
可知在匀减速运动阶段,游客的加速度大小
15.(1)8m/s2(2)会发生交通事故
【分析】
(1)根据司机低头看手机2s,相当于盲开40m,由位移时间关系求得汽车的行驶速度,由速度位移关系即可求解汽车刹车的最大加速度;
(2)汽车盲开和反应时间内都在做匀速直线运动,据速度位移关系求得匀速运动位移,刹车后做匀减速运动,由位移速度关系求得匀减速运动位移,再比较总位移与100m的大小确定是否发生交通事故.
【解析】(1)汽车运动的速度为
汽车刹车的最大加速度为a,则
(2)108km/h=30m/s
司机看手机时,汽车发生的位移为
x1=v2t=30×2=60m
反应时间内发生的位移的大小为
x2=v2△t=30×0.5=15m
刹车后汽车发生的位移
所以汽车前进的距离为x=x1+x2+x3=60+15+36=131.25m>130m
所以会发生交通事故.
【点睛】
掌握匀速直线运动和匀变速直线运动的位移时间关系,知道司机低头开的时间和反应时间内汽车做匀速直线运动,刹车后做匀减速直线运动,这是解决本题的关键.
16.
【解析】设甲开始的加速度为a,两段时间间隔都为t,则甲在两段时间内的总路程为:
乙在两段时间内的总路程为:
由上两式得
