北师大版2021-2022学年七年级数学上册2.3.1 相反数课件(共29张PPT)
文档属性
| 名称 | 北师大版2021-2022学年七年级数学上册2.3.1 相反数课件(共29张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 255.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-28 20:17:26 | ||
图片预览








文档简介
(共29张PPT)
2.3.1 相反数
七年级上册
借助数轴理解相反数的意义;
会求任意有理数的相反数
1
2
3
懂得数轴上表示相反数的两个点关于原点对称
本节目标
情境思考
有理数王国的公民+1一天不小心掉进了一个魔瓶里。谁知出来后竟变成胖乎乎的0,你说怪不怪?冷眼旁观的2说:“谁叫这瓶里睡着他的相反数兄弟呢?幸好我兄弟不在里面!”同学们,你想知道+1的相反数兄弟是谁?为什么他俩见面后就变成0呢?就让我们一起走进神奇的相反数的世界吧!
我怎么就变胖了呢?
哈哈!我还是我!
新课讲解
探究
在数轴上,与原点的距离是2的点有几个?这些点各表示哪个数?
设a是一个正数. 数轴上与原点的距离等于a的点有几个?这些点表示的数有什么关系?
新课讲解
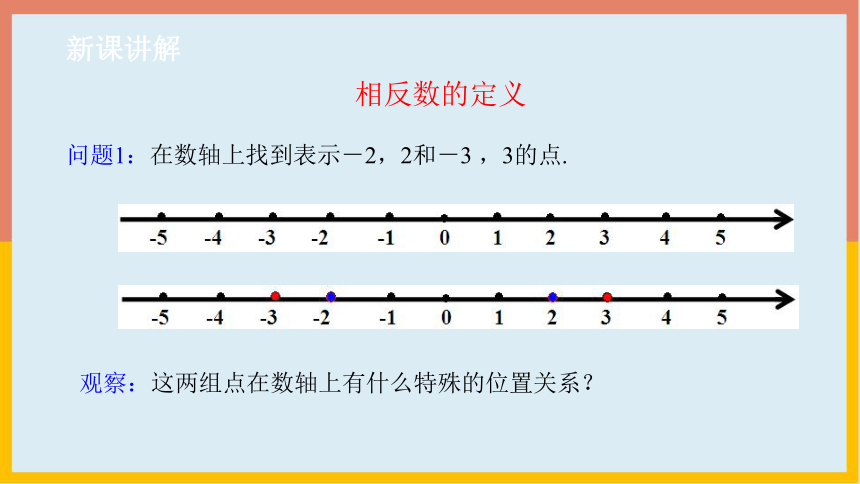
相反数的定义
问题1:在数轴上找到表示-2,2和-3 ,3的点.
观察:这两组点在数轴上有什么特殊的位置关系?
新课讲解
结论:表示每组中两个数的点都位于原点的两旁,且与原点的距离相等.
思考:你还能举出数轴上其它点的例子吗?
新课讲解
问题2:观察数轴,说出在数轴上与原点的距离是 2的点有几个?这些点各表示哪些数?设a是一个正数,数轴上与原点的距离等于a的点有几个?这些点表示的数有什么关系?
归纳总结
数轴上与原点的距离是 2的点有两个,表示为-2和2;如果a是一个正数,数轴上与原点的距离是a的点有两个,它们分别在原点左右,表示为-a和a,我们说这两个点关于原点对称.
新课讲解
只有符号不同的两个数叫做互为相反数. 特别地,
0的相反数是0.
定义
问题3:你能再举出几组互为相反数的数的例子吗?
新课讲解
1.相反数的代数意义:只有符号不同的两个数叫做互为相反数.特殊规定:0的相反数是0.
2.相反数的求法:求一个数的相反数就是在这个数的前面加上“-”号,即a的相反数是-a,其实质是改变这个数的符号.
新课讲解
例1 下列说法正确的是( )
A.-2是相反数
B. 与-2互为相反数
C.-3与+2互为相反数
D. 与0.5互为相反数
分析:判断两个数是否互为相反数,按其定义从两个方面去看:符号(+、-)和所含数字(相同).
D
新课讲解
(1)相反数不能单独存在,前提是“互为”;
(2)判断两个数是否互为相反数,要从两个方面看,
一是符号不能相同;
二是数字一定要相同.
新课讲解
例2 分别写出下列各数的相反数.
-3,2,4.5,0,- .
分析:根据相反数的代数意义(只有符号不同的两个数互为相反数),直接写出一个数的相反数.
解:-3的相反数是3,2的相反数是-2,
4.5的相反数是-4.5,0的相反数是0,
新课讲解
(1)在一个省略正号的正数的前面添加负号,即可得到这个数的相反数;
(2)直接去掉负数的负号即可得到它的相反数,0的相反数是0,任何有理数有且只有一个相反数.
相反数的性质
-2.5与+2.5,+1与-1,+3与-3
0
.
.
+2.5
-2.5
0
.
.
+1
-1
每一对数在数轴上的对应点位于原点的两侧,且到原点的距离相等.
新课讲解
-7表示__的相反数;
-(-7) 表示___的相反数.
在一个数的前面添上“-”号表示原来这个数的相反数.
在一个数的前面添上“+”号表示这个数本身.
7
-7
-7的相反数是7
辩 一 辩
a的相反数-a前有负号,那么-a一定是负数吗?
难道我穿男孩衣服就是男孩吗?嘻嘻!
当a是正数时,-a是负数
当a是零时,-a是零
当a是负数时,-a是正数
新课讲解
例题解析
例3、画一条数轴,并标出表示下列各数的相反数的点:
3, 1.5, -6
解:3的相反数是-3;1.5的相反数是-1.5;-6的相反数是6,且-3,-1.5,6在数轴上对应的点分别为A,B,C,如图所示
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6
A
B
C
·
·
·
一个数在数轴上所对应的点向右移动5个单位长度后得到它的相反数的对应点,则这个数是( )
A.-2 B.2 C.2 D.-2
变式训练
D
新课讲解
说一说
-(+1)= -(-1)=
因为+1的相反数是-1,
所以-(+1)=-1
因为-1的相反数是1,
所以-(-1)=1
归纳总结:
我们通常在一个数的前面加一个“—”号表示这个数的相反数。因此 –a 的相反数是 -(-a),另一方面,-a的相反数是a,所以-(-a)=a。
例4、填空:-(+0.8)= ; -(-3)= .
解:-(+0.8)= ; -(-3)= .
-0.8
3
例题解析
变式训练
化简下列各数:
⑴ -(+5) ⑵ +(-3) ⑶ +(+2) ⑷ -(-6)
解:(1) -(+5)=-5 (2) +(-3)=-3
(3) +(+2)=2 (4) -(-6)=6
多重符号的化简,一个正数前面不管它有多少个“+”,可以全部省去不写;一个正数前面有偶数个“-”号,也可以把“-”一起去掉;一个正数的前面有奇数个“-”号,则化简后只保留一个“-”号.
归纳总结
1.下列说法中正确的是( )
A、正数和负数互为相反数
B、任何一个数的相反数都与它本身不相同
C、任何一个数都有它的相反数
D、数轴上原点两旁的两个点表示的数互为相反数
2.相反数等于它本身的数一共有( )个
A、0 B.1 C.2 D.3
C
B
课堂练习
课堂练习
3.下列几组数中是互为相反数的是 ( )
A. 和0.7 B. 和-0.333 C. –(-6)和6 D. 和0.25
4.下列说法错误的是( )
A.6是-6的相反数 B.-6是-(-6)的相反数
C.-(+8)与+(-8)互为相反数 D.+(-8)与- (-8)互为相反数
C
D
拓展提升
5.已知a-3和-2互为相反数,求a与-a的值.
解:因为a-3和-2互为相反数
所以a-3+(-2)=0
所以a=5 -a=-5
本节总结
如果两个数只有符号不同,那么其中的一个数叫作另一个数的相反数,或者称它们互为相反数
化简
相反数
概念
多重符号的化简,一个正数前面不管它有多少个“+”,可以全部省去不写;一个正数前面有偶数个“-”号,也可以把“-”一起去掉;一个正数的前面有奇数个“-”号,则化简后只保留一个“-”号.
再见
2.3.1 相反数
七年级上册
借助数轴理解相反数的意义;
会求任意有理数的相反数
1
2
3
懂得数轴上表示相反数的两个点关于原点对称
本节目标
情境思考
有理数王国的公民+1一天不小心掉进了一个魔瓶里。谁知出来后竟变成胖乎乎的0,你说怪不怪?冷眼旁观的2说:“谁叫这瓶里睡着他的相反数兄弟呢?幸好我兄弟不在里面!”同学们,你想知道+1的相反数兄弟是谁?为什么他俩见面后就变成0呢?就让我们一起走进神奇的相反数的世界吧!
我怎么就变胖了呢?
哈哈!我还是我!
新课讲解
探究
在数轴上,与原点的距离是2的点有几个?这些点各表示哪个数?
设a是一个正数. 数轴上与原点的距离等于a的点有几个?这些点表示的数有什么关系?
新课讲解
相反数的定义
问题1:在数轴上找到表示-2,2和-3 ,3的点.
观察:这两组点在数轴上有什么特殊的位置关系?
新课讲解
结论:表示每组中两个数的点都位于原点的两旁,且与原点的距离相等.
思考:你还能举出数轴上其它点的例子吗?
新课讲解
问题2:观察数轴,说出在数轴上与原点的距离是 2的点有几个?这些点各表示哪些数?设a是一个正数,数轴上与原点的距离等于a的点有几个?这些点表示的数有什么关系?
归纳总结
数轴上与原点的距离是 2的点有两个,表示为-2和2;如果a是一个正数,数轴上与原点的距离是a的点有两个,它们分别在原点左右,表示为-a和a,我们说这两个点关于原点对称.
新课讲解
只有符号不同的两个数叫做互为相反数. 特别地,
0的相反数是0.
定义
问题3:你能再举出几组互为相反数的数的例子吗?
新课讲解
1.相反数的代数意义:只有符号不同的两个数叫做互为相反数.特殊规定:0的相反数是0.
2.相反数的求法:求一个数的相反数就是在这个数的前面加上“-”号,即a的相反数是-a,其实质是改变这个数的符号.
新课讲解
例1 下列说法正确的是( )
A.-2是相反数
B. 与-2互为相反数
C.-3与+2互为相反数
D. 与0.5互为相反数
分析:判断两个数是否互为相反数,按其定义从两个方面去看:符号(+、-)和所含数字(相同).
D
新课讲解
(1)相反数不能单独存在,前提是“互为”;
(2)判断两个数是否互为相反数,要从两个方面看,
一是符号不能相同;
二是数字一定要相同.
新课讲解
例2 分别写出下列各数的相反数.
-3,2,4.5,0,- .
分析:根据相反数的代数意义(只有符号不同的两个数互为相反数),直接写出一个数的相反数.
解:-3的相反数是3,2的相反数是-2,
4.5的相反数是-4.5,0的相反数是0,
新课讲解
(1)在一个省略正号的正数的前面添加负号,即可得到这个数的相反数;
(2)直接去掉负数的负号即可得到它的相反数,0的相反数是0,任何有理数有且只有一个相反数.
相反数的性质
-2.5与+2.5,+1与-1,+3与-3
0
.
.
+2.5
-2.5
0
.
.
+1
-1
每一对数在数轴上的对应点位于原点的两侧,且到原点的距离相等.
新课讲解
-7表示__的相反数;
-(-7) 表示___的相反数.
在一个数的前面添上“-”号表示原来这个数的相反数.
在一个数的前面添上“+”号表示这个数本身.
7
-7
-7的相反数是7
辩 一 辩
a的相反数-a前有负号,那么-a一定是负数吗?
难道我穿男孩衣服就是男孩吗?嘻嘻!
当a是正数时,-a是负数
当a是零时,-a是零
当a是负数时,-a是正数
新课讲解
例题解析
例3、画一条数轴,并标出表示下列各数的相反数的点:
3, 1.5, -6
解:3的相反数是-3;1.5的相反数是-1.5;-6的相反数是6,且-3,-1.5,6在数轴上对应的点分别为A,B,C,如图所示
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6
A
B
C
·
·
·
一个数在数轴上所对应的点向右移动5个单位长度后得到它的相反数的对应点,则这个数是( )
A.-2 B.2 C.2 D.-2
变式训练
D
新课讲解
说一说
-(+1)= -(-1)=
因为+1的相反数是-1,
所以-(+1)=-1
因为-1的相反数是1,
所以-(-1)=1
归纳总结:
我们通常在一个数的前面加一个“—”号表示这个数的相反数。因此 –a 的相反数是 -(-a),另一方面,-a的相反数是a,所以-(-a)=a。
例4、填空:-(+0.8)= ; -(-3)= .
解:-(+0.8)= ; -(-3)= .
-0.8
3
例题解析
变式训练
化简下列各数:
⑴ -(+5) ⑵ +(-3) ⑶ +(+2) ⑷ -(-6)
解:(1) -(+5)=-5 (2) +(-3)=-3
(3) +(+2)=2 (4) -(-6)=6
多重符号的化简,一个正数前面不管它有多少个“+”,可以全部省去不写;一个正数前面有偶数个“-”号,也可以把“-”一起去掉;一个正数的前面有奇数个“-”号,则化简后只保留一个“-”号.
归纳总结
1.下列说法中正确的是( )
A、正数和负数互为相反数
B、任何一个数的相反数都与它本身不相同
C、任何一个数都有它的相反数
D、数轴上原点两旁的两个点表示的数互为相反数
2.相反数等于它本身的数一共有( )个
A、0 B.1 C.2 D.3
C
B
课堂练习
课堂练习
3.下列几组数中是互为相反数的是 ( )
A. 和0.7 B. 和-0.333 C. –(-6)和6 D. 和0.25
4.下列说法错误的是( )
A.6是-6的相反数 B.-6是-(-6)的相反数
C.-(+8)与+(-8)互为相反数 D.+(-8)与- (-8)互为相反数
C
D
拓展提升
5.已知a-3和-2互为相反数,求a与-a的值.
解:因为a-3和-2互为相反数
所以a-3+(-2)=0
所以a=5 -a=-5
本节总结
如果两个数只有符号不同,那么其中的一个数叫作另一个数的相反数,或者称它们互为相反数
化简
相反数
概念
多重符号的化简,一个正数前面不管它有多少个“+”,可以全部省去不写;一个正数前面有偶数个“-”号,也可以把“-”一起去掉;一个正数的前面有奇数个“-”号,则化简后只保留一个“-”号.
再见
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
