对数函数与指数函数的关系
图片预览




文档简介
(共15张PPT)
函数
函数
函数
函数
3.2.3指数函数与对数函数的关系
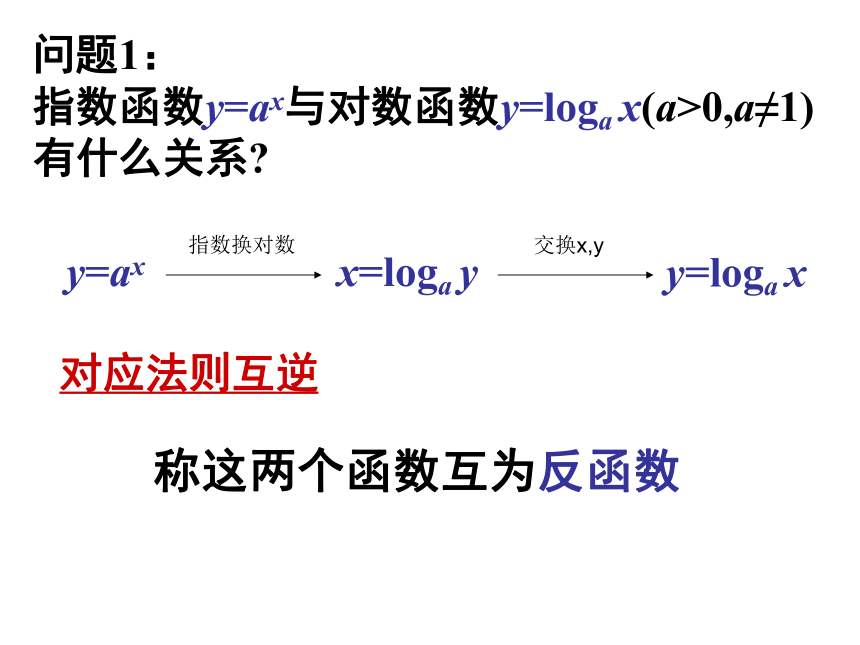
问题1:
指数函数y=ax与对数函数y=loga x(a>0,a≠1)有什么关系
称这两个函数互为反函数
对应法则互逆
y=ax
x=loga y
y=loga x
指数换对数
交换x,y
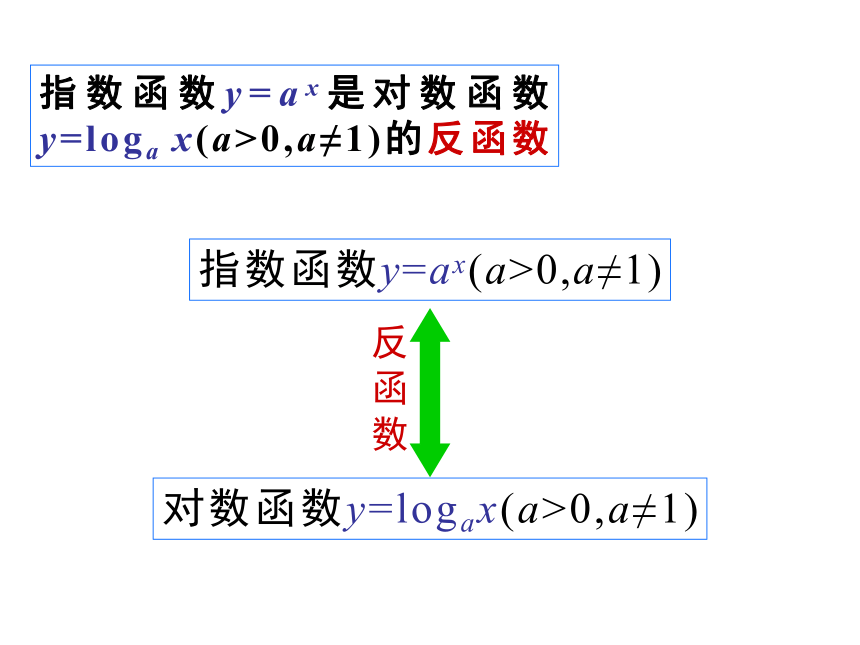
指数函数y=ax(a>0,a≠1)
对数函数y=logax(a>0,a≠1)
反函数
指数函数y=ax是对数函数y=loga x(a>0,a≠1)的反函数
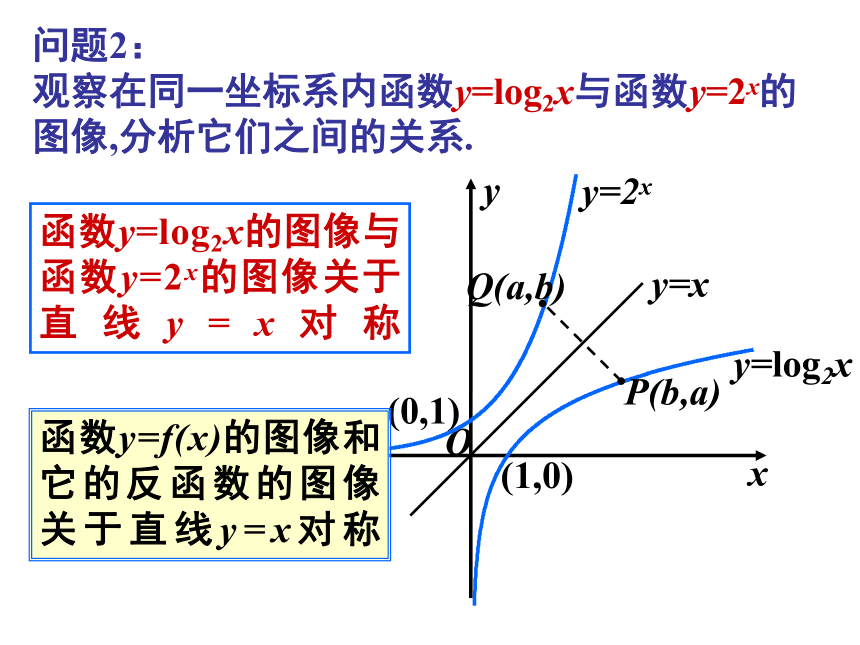
问题2:
观察在同一坐标系内函数y=log2x与函数y=2x的图像,分析它们之间的关系.
函数y=log2x的图像与函数y=2x的图像关于直线y=x对称
(1,0)
(0,1)
O
x
y
y=log2x
y=2x
y=x
P(b,a)
Q(a,b)
函数y=f(x)的图像和它的反函数的图像关于直线y=x对称
1.当一个函数是一一映射时,可以把这个函数的因变量作为一个新的函数的自变量,而把这个函数的自变量作为新的函数的因变量,我们称这两个函数互为反函数。
2.对数函数y=loga x与指数函数y=ax互为反函数,图象关于直线y=x对称。
3 .函数y=f(x)的反函数通常用y=f-1(x) 表示。
注意:y=f-1(x) 读作:“f逆x”
表示反函数,不是-1次幂(倒数)的意思
例1 写出下列对数函数的反函数:
(1)y =lgx;
解 (1)对数函数y=lgx,它的底数是
它的反函数是指数函数
10
y=10x
(2)对数函数
它的底数是
它的反函数是指数函数
例2 写出下列指数函数的反函数:
(1)y=5x
解(1)指数函数y=5x,它的底数是5
它的反函数是对数函数 y=log5x;
(2)指数函数 ,它的底数是 ,
它的反函数是对数函数
例3 求函数y=3x-2(x∈R)反函数,并在同一直角坐标系中作出函数及其反函数的图象。
解:由y=3x-2(x∈R )得
所以y=3x-2(x∈R)的反函数是
(x∈R )
y=3x-2 经过两点(0,-2), (2/3,0)
经过两点(-2,0), (0 ,2/3 )
0
x
y
y=3x-2
y=x
想一想:函数y=3x-2的图象和它的反函数
的图象之间有什么关系?
求函数反函数的步骤:
3 求原函数的值域
1 反解
2 x与y互换
4 写出反函数及它的定义域
b=f(a)
a=f-1(b)
点(b,a)在反函数y=f-1(x) 的图像上
点(a,b)在函数y=f(x)的图像上
(1,0)
(0,1)
O
x
y
y=log2x
y=2x
y=x
P(b,a)
Q(a,b)
结论:
[例4]函数f(x)=loga (x-1)(a>0且a≠1)的反函数的图象
经过点(1, 4),求a的值.
解:依题意,得
b=f(a)
a=f-1(b)
点(b,a)在反函数y=f-1(x) 的图像上
点(a,b)在函数y=f(x)的图像上
b=f(a)
a=f-1(b)
点(b,a)在反函数y=f-1(x) 的图像上
点(a,b)在函数y=f(x)的图像上
理论迁移
例4 已知函数 .
(1)求函数f(x)的定义域和值域;
(2)求证函数y=f(x)的图象关于直线
y=x对称.
小结
反函数的概念
定义域和值域互换
对应法则互逆
图像关于直线y=x对称
指数函数y=ax(a>0,a≠1)与对数函数y=logax(a>0,a≠1)
互为反函数
函数
函数
函数
函数
3.2.3指数函数与对数函数的关系
问题1:
指数函数y=ax与对数函数y=loga x(a>0,a≠1)有什么关系
称这两个函数互为反函数
对应法则互逆
y=ax
x=loga y
y=loga x
指数换对数
交换x,y
指数函数y=ax(a>0,a≠1)
对数函数y=logax(a>0,a≠1)
反函数
指数函数y=ax是对数函数y=loga x(a>0,a≠1)的反函数
问题2:
观察在同一坐标系内函数y=log2x与函数y=2x的图像,分析它们之间的关系.
函数y=log2x的图像与函数y=2x的图像关于直线y=x对称
(1,0)
(0,1)
O
x
y
y=log2x
y=2x
y=x
P(b,a)
Q(a,b)
函数y=f(x)的图像和它的反函数的图像关于直线y=x对称
1.当一个函数是一一映射时,可以把这个函数的因变量作为一个新的函数的自变量,而把这个函数的自变量作为新的函数的因变量,我们称这两个函数互为反函数。
2.对数函数y=loga x与指数函数y=ax互为反函数,图象关于直线y=x对称。
3 .函数y=f(x)的反函数通常用y=f-1(x) 表示。
注意:y=f-1(x) 读作:“f逆x”
表示反函数,不是-1次幂(倒数)的意思
例1 写出下列对数函数的反函数:
(1)y =lgx;
解 (1)对数函数y=lgx,它的底数是
它的反函数是指数函数
10
y=10x
(2)对数函数
它的底数是
它的反函数是指数函数
例2 写出下列指数函数的反函数:
(1)y=5x
解(1)指数函数y=5x,它的底数是5
它的反函数是对数函数 y=log5x;
(2)指数函数 ,它的底数是 ,
它的反函数是对数函数
例3 求函数y=3x-2(x∈R)反函数,并在同一直角坐标系中作出函数及其反函数的图象。
解:由y=3x-2(x∈R )得
所以y=3x-2(x∈R)的反函数是
(x∈R )
y=3x-2 经过两点(0,-2), (2/3,0)
经过两点(-2,0), (0 ,2/3 )
0
x
y
y=3x-2
y=x
想一想:函数y=3x-2的图象和它的反函数
的图象之间有什么关系?
求函数反函数的步骤:
3 求原函数的值域
1 反解
2 x与y互换
4 写出反函数及它的定义域
b=f(a)
a=f-1(b)
点(b,a)在反函数y=f-1(x) 的图像上
点(a,b)在函数y=f(x)的图像上
(1,0)
(0,1)
O
x
y
y=log2x
y=2x
y=x
P(b,a)
Q(a,b)
结论:
[例4]函数f(x)=loga (x-1)(a>0且a≠1)的反函数的图象
经过点(1, 4),求a的值.
解:依题意,得
b=f(a)
a=f-1(b)
点(b,a)在反函数y=f-1(x) 的图像上
点(a,b)在函数y=f(x)的图像上
b=f(a)
a=f-1(b)
点(b,a)在反函数y=f-1(x) 的图像上
点(a,b)在函数y=f(x)的图像上
理论迁移
例4 已知函数 .
(1)求函数f(x)的定义域和值域;
(2)求证函数y=f(x)的图象关于直线
y=x对称.
小结
反函数的概念
定义域和值域互换
对应法则互逆
图像关于直线y=x对称
指数函数y=ax(a>0,a≠1)与对数函数y=logax(a>0,a≠1)
互为反函数
