2021-2022学年人教版八年级数学上册14.2乘法公式 知识点分类辅导训练(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级数学上册14.2乘法公式 知识点分类辅导训练(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 327.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-29 14:22:59 | ||
图片预览

文档简介
2021-2022学年人教版八年级数学上册《14.2乘法公式》知识点分类优生辅导训练(附答案)
一.完全平方公式
1.若x满足(2021﹣x)2+(x﹣2020)2=2019,则(2021﹣x)(x﹣2020)的值是( )
A.﹣1006 B.﹣1007 C.﹣1008 D.﹣1009
2.若,x+=3,则= .
3.计算:= .
4.如图(1),大正方形的面积可以表示为(a+b)2,同时大正方形的面积也可以表示成两个小正方形面积与两个长方形的面积之和,即a2+2ab+b2.同一图形(大正方形)的面积,用两种不同的方法求得的结果应该相等,从而验证了完全平方公式:(a+b)2=a2+2ab+b2.
把这种“同一图形的面积,用两种不同的方法求出的结果相等,从而构建等式,根据等式解决相关问题”的方法称为“面积法”.
(1)用上述“面积法”,通过如图(2)中图形的面积关系,直接写出一个等式: .
(2)如图(3),Rt△ABC中,∠ACB=90°,CA=3,CB=4,AB=5,CH是斜边AB边上的高.用上述“面积法”求CH的长;
(3)如图(4),等腰△ABC中,AB=AC,点O为底边BC上任意一点,OM⊥AB,ON⊥AC,CH⊥AB,垂足分别为点M,N,H,连接AO,用上述“面积法”求证:OM+ON=CH.
5.(1)已知a2+b2=10,a+b=4,求a﹣b的值.
(2)关于x的代数式(ax﹣3)(2x+1)﹣2x2+m化简后不含x2项与常数项,且an2+mn=1,求2n3+5n2﹣5n+2022的值.
6.观察下面各式规律:12+(1×2)2+22=(1×2+1)2;22+(2×3)2+32=(2×3+1)2;32+(3×4)2+42=(3×4+1)2…写出第n行的式子,并证明你的结论.
二.完全平方公式的几何背景
7.如图,矩形ABCD的周长是10cm,以AB,AD为边向外作正方形ABEF和正方形ADGH,若正方形ABEF和ADGH的面积之和为17cm2,那么矩形ABCD的面积是( )
A.3cm2 B.4cm2 C.5cm2 D.6cm2
8.建党100周年主题活动中,浔浔设计了如图1的“红色徽章”其设计原理是:如图2,在边长为a的正方形EFGH四周分别放置四个边长为b的小正方形,构造了一个大正方形ABCD,并画出阴影部分图形,形成了“红色徽章”的图标.现将阴影部分图形面积记作S1,每一个边长为b的小正方形面积记作S2,若S1=6S2,则的值是 .
9.图1是一个长为2a、宽为2b的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形.
(1)求图2中的阴影部分的正方形的周长;
(2)观察图2,请写出下列三个代数式(a+b) ,(a﹣b) ,ab之间的等量关系;
(3)运用你所得到的公式,计算:若m、n为实数,且mn=﹣3,m﹣n=4,试求m+n的值.
(4)如图3,点C是线段AB上的一点,以AC、BC为边向两边作正方形,设AB=8,两正方形的面积和S1+S2=26,求图中阴影部分面积.
10.如图①是一个长为4a、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成一个“回形”正方形(如图②).
(1)根据上述过程,写出(a+b)2、(a﹣b)2、ab之间的等量关系: ;
(2)利用(2)中的结论,若x+y=4,xy=,则(x﹣y)2的值是 ;
(3)实际上通过计算图形的面积可以探求相应的等式,如图③,请你写出这个等式: ;
(4)如图④,点C是线段AB上的一点,分别以AC、BC为边在AB的同侧作正方形ACDE和正方形CBFG,连接EG、BG、BE,当BC=1时,△BEG的面积记为S1,当BC=2时,△BEG的面积记为S2…,以此类推,当BC=n时,△BEG的面积记为Sn时,试求S2021﹣S2020的值.
11.如图1,用4个相同边长是x,y的长方形和中间一个小正方形密铺而形成的大正方形.
(1)若大正方形的面积为36,小正方形的面积为4,则x﹣y值为 ;则x+y的值为 ;
(2)若小长方形两边长为9﹣m和m﹣4,则大正方形的边长为 ;若满足(9﹣m)(m﹣4)=4,则(9﹣m)2+(m﹣4)2的值为 ;
(3)如图2,正方形ABCD的边长是c,它由四个直角边长分别是a,b的直角三角形和中间一个小正方形组成的,猜想a,b,c三边的数量关系,并说明理由.
12.数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是长为b,宽为a的长方形.并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图2的大正方形.
(1)请用两种不同的方法求图2大正方形的面积:方法1: ;方法2: ;
(2)观察图2,请你写出代数式:(a+b)2,a2+b2,ab之间的等量关系 ;
(3)根据(2)题中的等量关系,解决如下问题:
①已知:a+b=5,a2+b2=13,求ab的值;
②已知(2020﹣a)2+(a﹣2019)2=5,求(2020﹣a)(a﹣2019)的值;
③已知(a﹣2019)2+(a﹣2021)2=8,则求(a﹣2020)2的值.
13.有两个正方形A,B,现将B放在A的内部得图甲,将A,B并列放置后构造新的正方形得图乙.若图甲和图乙中阴影部分的面积分别为1和12,求
(1)正方形A,B的面积之和为 .
(2)三个正方形A和两个正方形B如图丙摆放,求阴影部分的面积.
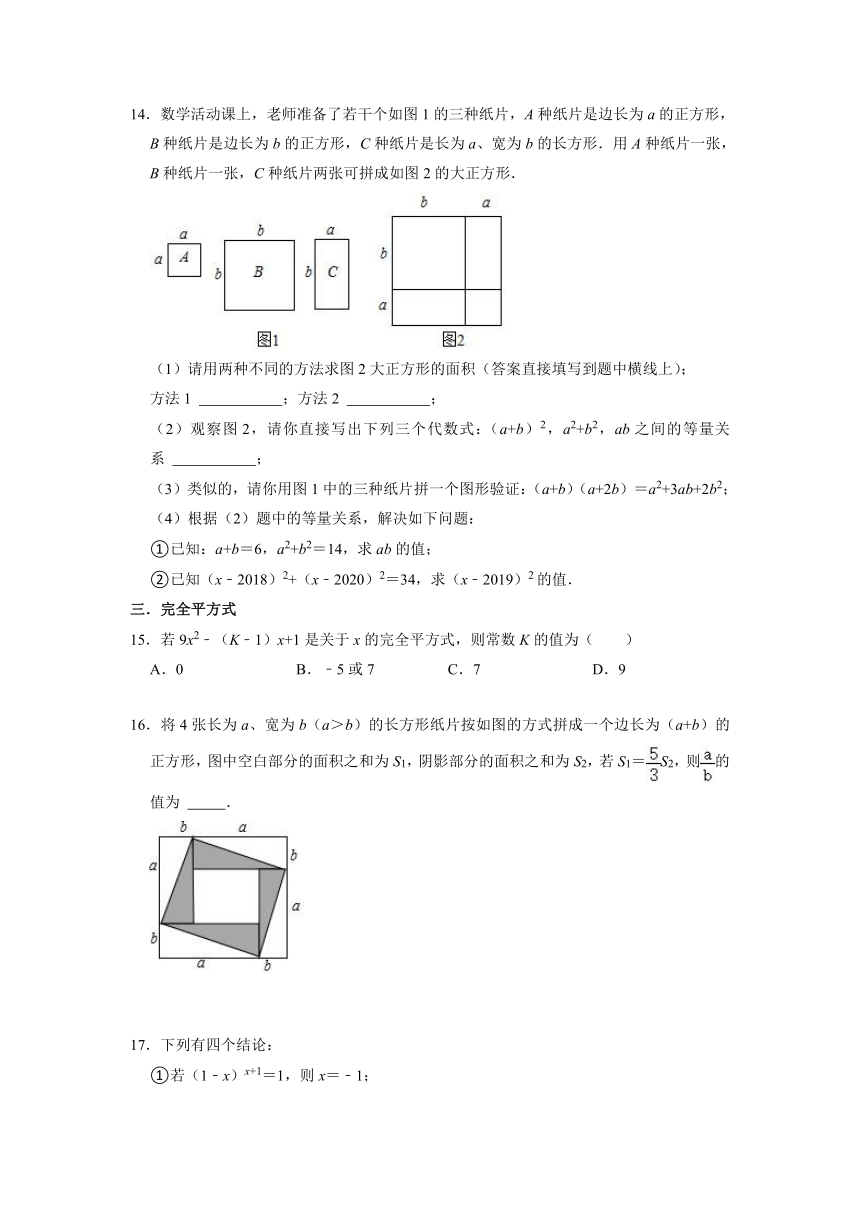
14.数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是长为a、宽为b的长方形.用A种纸片一张,B种纸片一张,C种纸片两张可拼成如图2的大正方形.
(1)请用两种不同的方法求图2大正方形的面积(答案直接填写到题中横线上);
方法1 ;方法2 ;
(2)观察图2,请你直接写出下列三个代数式:(a+b)2,a2+b2,ab之间的等量关系 ;
(3)类似的,请你用图1中的三种纸片拼一个图形验证:(a+b)(a+2b)=a2+3ab+2b2;
(4)根据(2)题中的等量关系,解决如下问题:
①已知:a+b=6,a2+b2=14,求ab的值;
②已知(x﹣2018)2+(x﹣2020)2=34,求(x﹣2019)2的值.
三.完全平方式
15.若9x2﹣(K﹣1)x+1是关于x的完全平方式,则常数K的值为( )
A.0 B.﹣5或7 C.7 D.9
16.将4张长为a、宽为b(a>b)的长方形纸片按如图的方式拼成一个边长为(a+b)的正方形,图中空白部分的面积之和为S1,阴影部分的面积之和为S2,若S1=S2,则的值为 .
17.下列有四个结论:
①若(1﹣x)x+1=1,则x=﹣1;
②若a2+b2=3,a﹣b=1,则(2﹣a)(2﹣b)的值为5﹣2;
③若规定:当ab≠0时,a b=a+b﹣ab,若a (4﹣a)=0,则a=2;
④若4x=a,8y=b,则24x﹣3y可表示为;
⑤已知多项式x2+4x+m是完全平方式,则常数m=4.
其中正确的是 .(填序号)
18.先阅读下面的内容,再解决问题
例题:若m2+2mn+2n2﹣6n+9=0,求m和n的值
解:∵m2+2mn+2n2﹣6n+9=0
∴m2+2mn+n2+n2﹣6n+9=0
∴(m+n)2+(n﹣3)2=0
∴m+n=0,n﹣3=0
∴m=﹣3,n=3
问题:(1)若x2+2y2﹣2xy+4y+4=0,求y2的值;
(2)试探究关于x、y的代数式5x2+9y2﹣12xy﹣6x+2028是否有最小值,若存在,求出最小值及此时x、y的值;若不存在,说明理由
19.湘一“追逐梦想”数学兴趣小组编了一个“诗 远方”的计算程序,规定:输入数据x,y时,若输出的是代数式称为“诗S”,若输出的是等式称为“远方M”.回答下列问题:
(1)当输入正整数x,y时,得到“远方M”和“诗S”,若“远方M”为2y=x2﹣1,求证“诗S”:2(x+y+1)是完全平方式.(温馨提示:对于一个整式A,如果存在另一个整式B,使A=B2的条件,则称A是完全平方式,比如(a+b)2=a2+2ab+b2,(a﹣b)2=a2﹣2ab+b2是完全平方式.)
(2)当输入x,y时,求“远方M”:x(x﹣1)+xy+y=51的x,y的正整数解.
(3)若正数x,y互为倒数,求“诗S”:S=的最小值.
四.平方差公式
20.(3+1)×(32+1)×(34+1)×……×(332+1)+的值为 .
21.阅读下列材料:已知实数m,n满足(2m2+n2+1)(2m2+n2﹣1)=80,试求2m2+n2的值.
解:设2m2+n2=t,则原方程变为(t+1)(t﹣1)=80,整理得t2﹣1=80,即t2=81,
∴t=±9.
∵2m2+n2≥0,
∴2m2+n2=9.
上面这种方法称为“换元法”,换元法是数学学习中最常用的一种思想方法,在结构较复杂的数和式的运算中,若把其中某些部分看成一个整体,并用新字母代替(即换元),则能使复杂的问题简单化.
根据以上阅读材料内容,解决下列问题,并写出解答过程.
(1)已知实数x,y满足(2x2+2y2+3)(2x2+2y2﹣3)=27,求x2+y2的值.
(2)若四个连续正整数的积为120,求这四个连续正整数.
22.你能求(x﹣1)(x2022+x2021+x2020+…+x+1)的值吗?遇到这样的问题,我们可以先思考从简单的情形入手,先分别计算下列各式的值:
①(x﹣1)(x+1)=x2﹣1;
②(x﹣1)(x2+x+1)=x3﹣1;
③(x﹣1)(x3+x2+x+1)=x4﹣1;
…
(1)由此我们可以得到:(x﹣1)(x2022+x2021+x2020+…+x+1)= ;
(2)请你利用上面的结论,完成下面的计算:
①22022+22021+22020+…+2+1;
②(﹣2)2022+(﹣2)2021+(﹣2)2020+…+(﹣2)+1.
23.张老师在黑板上写了三个算式,希望同学们认真观察,发现规律.请你结合这些算式,解答下列问题:
请观察以下算式:
①32﹣12=8×1
②52﹣32=8×2
③72﹣52=8×3
(1)请你再写出另外两个符合上述规律的算式;
(2)验证规律:设两个连续奇数为2n+1,2n﹣1(其中n为正整数),则它们的平方差是8的倍数;
(3)拓展延伸:“两个连续偶数的平方差是8的倍数”,这个结论正确吗?
五.平方差公式的几何背景
24.【探究】如图①,从边长为a的大正方形中剪掉一个边长为b的小正方形,将阴影部分沿虚线剪开,拼成图②的长方形
(1)请你分别表示出这两个图形中阴影部分的面积
(2)比较两图的阴影部分面积,可以得到乘法公式: (用字母表示)
【应用】请应用这个公式完成下列各题
①已知4m2﹣n2=12,2m+n=4,则2m﹣n的值为
②计算:(2a+b﹣c)(2a﹣b+c)
【拓展】①(2+1)(22+1)(24+1)(28+1)…(232+1)+1结果的个位数字为
②计算:1002﹣992+982﹣972+…+42﹣32+22﹣12
参考答案
一.完全平方公式
1.解:设2021﹣x=a,x﹣2020=b,则(2021﹣x)2+(x﹣2020)2=a2+b2=2019,a+b=(2021﹣x)+(x﹣2020)=1,
所以,(2021﹣x)(x﹣2020)=ab=[(a+b)2﹣(a2+b2)]=×(12﹣2019)=﹣1009;
故选:D.
2.解:∵x+=3,
∴(x+)2=9,
即x2+=7,
∴(x2+)2=49,
∴x4+=47,
(x+)3=27,
∴x3++3(x2 + x)=27,
即x3+=18,
∴==.
故答案为:.
3.解:∵202320212+202320232﹣2,
=(20232022﹣1)2+(20232022+1)2﹣2,
=2×202320222,
∴=.
故答案为:.
4.解:(1)如图(2),大正方形的面积为一个正方形的面积与三个小长方形面积之和,
即x2+5x+6,
同时大长方形的面积也可以为(x+3)(x+2),
所以x2+5x+6=(x+3)(x+2);
故答案为:x2+5x+6=(x+3)(x+2);
(2)如图(3),Rt△ABC中,∠C=90°,CA=3,CB=4,AB=5,
∵S△ABC=AC BC=AB CH,
∴CH===;
答:CH的长为;
(3)证明:如图(4),
∵OM⊥AB,ON⊥AC,CH⊥AB,垂足分别为点M,N,H,
∴S△ABC=S△ABO+S△AOC,
∴AB CH=AB OM+AC ON,
∵AB=AC,
∴CH=OM+ON.
即OM+ON=CH.
5.解:(1)∵a2+b2=10,a+b=4.
∴(a+b)2=a2+b2+2ab.
∴2ab=16﹣10=6.
∴(a﹣b)2=a2+b2﹣2ab=4.
∴a﹣b=±2.
(2)∵(ax﹣3)(2x+1)﹣2x2+m
=2ax2+ax﹣6x﹣3﹣2x2+m
=(2a﹣2)x2+(a﹣6)x+m﹣3.
∵不含x2项与常数项.
∴2a﹣2=0,m﹣3=0.
∴a=1,m=3.
∵an2+mn=1.
∴n2+3n=1.
∴2n3+5n2﹣5n+2022=2n3+6n2﹣n2﹣5n+2022.
=2n(n2+3n)﹣n2﹣5n+2022
=2n﹣n2﹣5n+2022
=﹣(n2+3n)+2022
=﹣1+2022
=2021.
6.解:第n个式子:n2+[n(n+1)]2+(n+1)2=[n(n+1)+1]2,
证明:因为左边=n2+[n(n+1)]2+(n+1)2,
=n2+(n2+n)2+(n+1)2,
=(n2+n)2+2n2+2n+1,
=(n2+n)2+2(n2+n)+1,
=(n2+n+1)2,
而右边=(n2+n+1)2,
所以,左边=右边,等式成立.
二.完全平方公式的几何背景(共8小题)
7.解:设AB=x,AD=y,
∵正方形ABEF和ADGH的面积之和为17cm2
∴x2+y2=17,
∵矩形ABCD的周长是10cm
∴2(x+y)=10,
∵(x+y)2=x2+2xy+y2,
∴25=17+2xy,
∴xy=4,
∴矩形ABCD的面积为:xy=4cm2,
故选:B.
8.解:∵S1=(a+2b)2﹣b2﹣a(a+2b)﹣b2﹣(a+b)2=2ab+b2,S2=b2,S1=6S2,
∴2ab+b2=6b2,
∴.
故答案为:.
9.解:(1)阴影部分的正方形边长为a﹣b,故周长为4(a﹣b)=4a﹣4b,
故答案为:4a﹣4b;
(2)大正方形面积可以看作四个矩形面积加阴影面积,故可表示为:4ab+(a﹣b) ,
大正方形边长为a+b,故面积也可以表达为:(a+b) ,
因此(a+b) =(a﹣b) +4ab,
故答案为:(a+b) =(a﹣b) +4ab;
(3)由(2)可知:(m+n) =(m﹣n) +4mn,
已知m﹣n=4,mn=﹣3,
所以(m+n) =16+4×(﹣3)=4,
所以m+n=±2;
故m+n的值为±2;
(4)设AC=a,BC=b,
因为AB=8,S1+S2=26,
所以a+b=8,a +b =26,
因为(a+b) =a +b +2ab,
所以64=26+2ab,解得ab=19,
由题意:∠ACF=90°,
所以S阴影=ab=.
10.解:(1)由图①和图②中矩形的面积为等量得:
4ab=(a+b)2﹣(a﹣b)2,
故答案为:4ab=(a+b)2﹣(a﹣b)2;
(2)由(1)中公式可得:(a﹣b)2=(a+b)2﹣4ab.
同理可得:
(x﹣y)2=(x+y)2﹣4xy
=
=7,
故答案为:7;
(3)分别以大矩形的面积和几个小矩形的面积为等量可得:
(3a+b)(a+b)=3a2+4ab+b2,
故答案为:(3a+b)(a+b)=3a2+4ab+b2;
(4)在正方形ACDE和正方形BCGF中,
∠ECD=∠CGB=45°,
∴EC∥BG,
∴S△BGE=S△BGC.
当BC=1时,,
当BC=2时,,
……
当BC=n时,,
∴S2021﹣S2020
=
=
=.
11.解:(1)∵大正方形的面积为36,小正方形的面积为4,
∴(x+y)2=36,(x﹣y)2=4,
又∵x>y>0,
∴x+y=6,x﹣y=2,
故答案为:2,6;
(2)大正方形的边长为x+y=9﹣m+m﹣4=5,
∵(9﹣m)(m﹣4)=4,
∴(9﹣m)2+(m﹣4)2=[(9﹣m)+(m﹣4)]2﹣2(9﹣m)(m﹣4)=52﹣8=17,
故答案为:5,17;
(3)a,b,c三边的数量关系为a2+b2=c2.理由如下:
由拼图可得,小正方形的边长为a﹣b,
由大正方形的面积等于小正方形的面积与4个直角三角形的面积和可得,
(a﹣b)2+ab×4=c2,
即a2+b2=c2.
12.解:(1)方法1:图2是边长为(a+b)的正方形,
∴S正方形=(a+b)2;
方法2:图2可看成1个边长为a的正方形、1个边长为b的正方形以及2个长为b宽为a的长方形的组合体,
∴S正方形=a2+b2+2ab.
故答案为:(a+b)2;a2+b2+2ab;
(2)由(1)可得:(a+b)2=a2+2ab+b2.
故答案为:(a+b)2=a2+2ab+b2
(3)①∵a+b=5,
∴(a+b)2=25,
∴a2+b2+2ab=25,
又∵a2+b2=13,
∴ab=6;
②设2020﹣a=x,a﹣2019=y,则x+y=1,
∵(2020﹣a)2+(a﹣2019)2=5,
∴x2+y2=5,
∵(x+y)2=x2+2xy+y2,
∴xy===﹣2,
即(2020﹣a)(a﹣2019)=xy=﹣2;
③设a﹣2019=x,a﹣2021=y,则x﹣y=2,
∵(a﹣2019)2+(a﹣2021)2=8,
∴x2+y2=8,
∵(x﹣y)2=x2﹣2xy+y2,
∴xy=,
∵x﹣y=2,即y=x﹣2,
∴(a﹣2020)2=(a﹣2000)(a﹣2000)=(x﹣1)(y+1)=xy+x﹣y﹣1=3.
13.解:(1)设正方形A,B的边长分别为a,b(a>b),
由图甲得(a﹣b)2=1,由图乙得(a+b)2﹣a2﹣b2=12
得ab=6,a2+b2=13,
故答案为:13;
(2)∵ab=6,a2+b2=13,
∴(a+b)2=(a﹣b)2+4ab=1+24=25,
∵a+b>0,
∴a+b=5,
∵(a﹣b)2=1,
∴a﹣b=1,
∴图丙的阴影部分面积S=(2a+b)2﹣3a2﹣2b2=a2﹣b2+4ab=(a﹣b)(a+b)+4ab=5+24=29.
14.解:(1)图2是边长为(a+b)的正方形,因此面积为(a+b)2,
图2可以看作4个部分的面积和,即为a2+2ab+b2,
故答案为:(a+b)2,a2+2ab+b2;
(2)由(1)的两种方法计算图形的面积可得,(a+b)2=a2+2ab+b2;
(3)如图,可以验证:(a+b)(a+2b)=a2+3ab+2b2;
(4)①∵a+b=6,a2+b2=14,
∴2ab=(a+b)2﹣(a2+b2)=36﹣14=22,
即ab=11,
②设a=x﹣2018,b=x﹣2020,则a﹣b=2,a2+b2=34,=x﹣2019,
∴2ab=(a2+b2)﹣(a﹣b)2=34﹣4=30,
∴(x﹣2019)2=()2===16,
答:(x﹣2019)2的值为16.
三.完全平方式
15.解:9x2﹣(K﹣1)x+1=(3x)2﹣(K﹣1)x+12.
∵9x2﹣(K﹣1)x+1是关于x的完全平方式,
∴9x2﹣(K﹣1)x+1=(3x)2±2 3x 1+12=(3x)2±6x+12.
∴﹣(K﹣1)=±6.
当﹣(K﹣1)=6时,K=﹣5.
当﹣(K﹣1)=﹣6时,K=7.
综上:K=﹣5或7.
故选:B.
16.解:S1=4×ab+(a﹣b)2
=2ab+a2﹣2ab+b2
=a2+b2,
S2=()2﹣(a﹣b)2
=a2+b2﹣a2+2ab﹣b2
=2ab,
∵S1=S2,
∴a2+b2= 2ab,
∴3a2﹣10ab+3b2=0,
(3a﹣b)(a﹣3b)=0,
∴3a﹣b=0或a﹣3b=0,
解得:a=b或a=3b,
∵a>b>0,
∴a=b舍去,
当a=3b时,==3,
故答案为:3.
17.解:①可以分为三种情况:
当x+1=0时,x=﹣1;
当1﹣x=1时,x=0;
当1﹣x=﹣1,x+1为偶数时,x=2,但x+1=3不是偶数,舍去;
综上所述,x=﹣1或0.
∴①不符合题意;
②(2﹣a)(2﹣b)
=4﹣2b﹣2a+ab
=4﹣2(a+b)+ab,
∵a﹣b=1,
∴(a﹣b)2=1,
∴a2+b2﹣2ab=1,
∴ab=1,
∴(a+b)2=a2+b2+2ab=3+2=5,
∴a+b=±,
当a+b=时,原式=4﹣2+1=5﹣2;
当a+b=﹣时,原式=4+2+1=5+2,
∴a+b=5±2.
∴②不符合题意;
③根据定义得:a+4﹣a+a(4﹣a)=0,
解得:a=2,
∴③符合题意;
④∵4x=(22)x=22x,8y=(23)y=23y,
∴24x﹣3y===,
∴④不符合题意;
⑤∵x2+4x+m是完全平方式,
∴m=()2=4,
∴⑤符合题意,
故答案为:③⑤.
18.解:(1)∵x2+2y2﹣2xy+4y+4=0,
∴(x﹣y)2+(y+2)2=0,
∴x﹣y=0,y+2=0,
x=y=﹣2.
∴y2=(﹣2)2=4;
(2)∵5x2+9y2﹣12xy﹣6x+2028
=(4x2+9y2﹣12xy)+(x2﹣6x+9)+2019
=(2x﹣3y)2+(x﹣3)2+2019.
∵(2x﹣3y)2≥0,(x﹣3)2≥0,
∴(2x﹣3y)2+(x﹣3)2+2019≥2019.
∴当2x﹣3y=0,x﹣3=0时,即当x=3,y=2时,代数式5x2+9y2﹣12xy﹣6x+2028有最小值2019.
19.解:2y=x2﹣1代入2(x+y+1),得
2(x+y+1)
=2x+2y+2
=2x+x2﹣1+2
=x2+2x+1
=(x+1)2
为完全平方式.
(2)∵x(x﹣1)+xy+y=51
∴x2﹣x﹣2+xy+y=49
(x+1)(x﹣2)+y(x+1)=49
(x+1)(x+y﹣2)=49
∵x,y都是正整数,
∴或或
解得或(舍去)或(舍去),
∴x,y的正整数解为6和3;
(3)∵正数x,y互为倒数,
∴xy=1
S=
=
=1﹣
当x+2y取最小值时,S有最小值,
∵x+2y≥2=2
即x=,y=
S=1﹣
=1+2﹣3
=2﹣2.
答:“诗S”:S=的最小值为2﹣2.
四.平方差公式
20.解:原式=(3﹣1)×(3+1)×(32+1)×(34+1)×……×(332+1)+
=(32﹣1)×(32+1)×(34+1)×……×(332+1)+
=(34﹣1)×(34+1)×……×(332+1)+
=(38﹣1)×……×(332+1)+
=(364﹣1)+
=﹣+
=.
21.解:(1)设2x2+2y2=m,则(m+3)(m﹣3)=27,
∴m2﹣9=27,即m2=36,∴m=±6,
∵2x2+2y2≥0,∴2x2+2y2=6,
∴x2+y2=3;
(2)设最小数为x,则x(x+1)(x+2)(x+3)=120,
即:(x2+3x)(x2+3x+2)=120,
设x2+3x=y,则y2+2y﹣120=0,
∴y1=﹣12,y2=10,
∵x为正整数,
∴y=x2+3x=10,
∴x1=2,x2=﹣5<0(舍去),
∴这四个整数为2,3,4,5.
22.解:(1)根据规律,原式=x2023﹣1,
故答案为:x2023﹣1;
(2)①规律用字母表示为:(x﹣1)(xn+xn﹣1+...+x+1)=xn+1﹣1,
当x=2,n=2022时,
(2﹣1)(22022+22021+22020+...+2+1)=22023﹣1,
∴22022+22021+22020+...+2+1=22023﹣1;
②当x=﹣2,n=2022时,
(﹣2﹣1)[(﹣2)2022+(﹣2)2021+(﹣2)2020+...+(﹣2)+1]=(﹣2)2023﹣1,
∴(﹣2)2022+(﹣2)2021+(﹣2)2020+...+(﹣2)+1=.
23.解:(1)92﹣72=8×4,112﹣92=8×5;
(2)验证规律:设两个连续奇数为2n+1,2n﹣1(其中n为正整数),
则它们的平方差是8的倍数;
(2n+1)2﹣(2n﹣1)2=(2n+1﹣2n+1)(2n+1+2n﹣1)=2×4n=8n
故两个连续奇数的平方差是8的倍数.
(3)拓展延伸:“两个连续偶数的平方差是8的倍数”,这个结论正确吗?
不正确.
解法一:举反例:42﹣22=12,
因为12不是8的倍数,故这个结论不正确.
解法二:设这两个偶数为2n和2n+2,(2n+2)2﹣(2n)2=(2n+2﹣2n)(2n+2+2n)=8n+4
因为8n+4不是8的倍数,故这个结论不正确.
五.平方差公式的几何背景
24.解:(1)图①按照正方形面积公式可得:a2﹣b2;
图②按照长方形面积公式可得:(a+b)(a﹣b).
故答案为:a2﹣b2;(a+b)(a﹣b).
(2)令(1)中两式相等可得:(a+b)(a﹣b)=a2﹣b2
故答案为:(a+b)(a﹣b)=a2﹣b2.
【应用】①∵4m2﹣n2=12,2m+n=4,4m2﹣n2=(2m+n)(2m﹣n)
∴(2m﹣n)=12÷4=3
故答案为:3.
②(2a+b﹣c)(2a﹣b+c)
=[2a+(b﹣c)][2a﹣(b﹣c)]
=4a2﹣(b﹣c)2
=4a2﹣b2+2bc﹣c2
【拓展】①
原式=(2﹣1)(2+1)(22+1)(24+1)(28+1)…(232+1)+1
=(22﹣1)(22+1)(24+1)(28+1)…(232+1)+1
=(24﹣1)(24+1)(28+1)…(232+1)+1
=(28﹣1)(28+1)…(232+1)+1
=(216﹣1)…(232+1)+1
=264﹣1+1
=264
∵2的正整数次方的尾数为2,4,8,6循环,64÷4=16
故答案为:6.
②原式=(100+99)(100﹣99)+(98+97)(98﹣97)+…+(4+3)(4﹣3)+(2+1)(2﹣1)
=100+99+98+97+…+4+3+2+1
=5050
一.完全平方公式
1.若x满足(2021﹣x)2+(x﹣2020)2=2019,则(2021﹣x)(x﹣2020)的值是( )
A.﹣1006 B.﹣1007 C.﹣1008 D.﹣1009
2.若,x+=3,则= .
3.计算:= .
4.如图(1),大正方形的面积可以表示为(a+b)2,同时大正方形的面积也可以表示成两个小正方形面积与两个长方形的面积之和,即a2+2ab+b2.同一图形(大正方形)的面积,用两种不同的方法求得的结果应该相等,从而验证了完全平方公式:(a+b)2=a2+2ab+b2.
把这种“同一图形的面积,用两种不同的方法求出的结果相等,从而构建等式,根据等式解决相关问题”的方法称为“面积法”.
(1)用上述“面积法”,通过如图(2)中图形的面积关系,直接写出一个等式: .
(2)如图(3),Rt△ABC中,∠ACB=90°,CA=3,CB=4,AB=5,CH是斜边AB边上的高.用上述“面积法”求CH的长;
(3)如图(4),等腰△ABC中,AB=AC,点O为底边BC上任意一点,OM⊥AB,ON⊥AC,CH⊥AB,垂足分别为点M,N,H,连接AO,用上述“面积法”求证:OM+ON=CH.
5.(1)已知a2+b2=10,a+b=4,求a﹣b的值.
(2)关于x的代数式(ax﹣3)(2x+1)﹣2x2+m化简后不含x2项与常数项,且an2+mn=1,求2n3+5n2﹣5n+2022的值.
6.观察下面各式规律:12+(1×2)2+22=(1×2+1)2;22+(2×3)2+32=(2×3+1)2;32+(3×4)2+42=(3×4+1)2…写出第n行的式子,并证明你的结论.
二.完全平方公式的几何背景
7.如图,矩形ABCD的周长是10cm,以AB,AD为边向外作正方形ABEF和正方形ADGH,若正方形ABEF和ADGH的面积之和为17cm2,那么矩形ABCD的面积是( )
A.3cm2 B.4cm2 C.5cm2 D.6cm2
8.建党100周年主题活动中,浔浔设计了如图1的“红色徽章”其设计原理是:如图2,在边长为a的正方形EFGH四周分别放置四个边长为b的小正方形,构造了一个大正方形ABCD,并画出阴影部分图形,形成了“红色徽章”的图标.现将阴影部分图形面积记作S1,每一个边长为b的小正方形面积记作S2,若S1=6S2,则的值是 .
9.图1是一个长为2a、宽为2b的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形.
(1)求图2中的阴影部分的正方形的周长;
(2)观察图2,请写出下列三个代数式(a+b) ,(a﹣b) ,ab之间的等量关系;
(3)运用你所得到的公式,计算:若m、n为实数,且mn=﹣3,m﹣n=4,试求m+n的值.
(4)如图3,点C是线段AB上的一点,以AC、BC为边向两边作正方形,设AB=8,两正方形的面积和S1+S2=26,求图中阴影部分面积.
10.如图①是一个长为4a、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成一个“回形”正方形(如图②).
(1)根据上述过程,写出(a+b)2、(a﹣b)2、ab之间的等量关系: ;
(2)利用(2)中的结论,若x+y=4,xy=,则(x﹣y)2的值是 ;
(3)实际上通过计算图形的面积可以探求相应的等式,如图③,请你写出这个等式: ;
(4)如图④,点C是线段AB上的一点,分别以AC、BC为边在AB的同侧作正方形ACDE和正方形CBFG,连接EG、BG、BE,当BC=1时,△BEG的面积记为S1,当BC=2时,△BEG的面积记为S2…,以此类推,当BC=n时,△BEG的面积记为Sn时,试求S2021﹣S2020的值.
11.如图1,用4个相同边长是x,y的长方形和中间一个小正方形密铺而形成的大正方形.
(1)若大正方形的面积为36,小正方形的面积为4,则x﹣y值为 ;则x+y的值为 ;
(2)若小长方形两边长为9﹣m和m﹣4,则大正方形的边长为 ;若满足(9﹣m)(m﹣4)=4,则(9﹣m)2+(m﹣4)2的值为 ;
(3)如图2,正方形ABCD的边长是c,它由四个直角边长分别是a,b的直角三角形和中间一个小正方形组成的,猜想a,b,c三边的数量关系,并说明理由.
12.数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是长为b,宽为a的长方形.并用A种纸片一张,B种纸片一张,C种纸片两张拼成如图2的大正方形.
(1)请用两种不同的方法求图2大正方形的面积:方法1: ;方法2: ;
(2)观察图2,请你写出代数式:(a+b)2,a2+b2,ab之间的等量关系 ;
(3)根据(2)题中的等量关系,解决如下问题:
①已知:a+b=5,a2+b2=13,求ab的值;
②已知(2020﹣a)2+(a﹣2019)2=5,求(2020﹣a)(a﹣2019)的值;
③已知(a﹣2019)2+(a﹣2021)2=8,则求(a﹣2020)2的值.
13.有两个正方形A,B,现将B放在A的内部得图甲,将A,B并列放置后构造新的正方形得图乙.若图甲和图乙中阴影部分的面积分别为1和12,求
(1)正方形A,B的面积之和为 .
(2)三个正方形A和两个正方形B如图丙摆放,求阴影部分的面积.
14.数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片是边长为a的正方形,B种纸片是边长为b的正方形,C种纸片是长为a、宽为b的长方形.用A种纸片一张,B种纸片一张,C种纸片两张可拼成如图2的大正方形.
(1)请用两种不同的方法求图2大正方形的面积(答案直接填写到题中横线上);
方法1 ;方法2 ;
(2)观察图2,请你直接写出下列三个代数式:(a+b)2,a2+b2,ab之间的等量关系 ;
(3)类似的,请你用图1中的三种纸片拼一个图形验证:(a+b)(a+2b)=a2+3ab+2b2;
(4)根据(2)题中的等量关系,解决如下问题:
①已知:a+b=6,a2+b2=14,求ab的值;
②已知(x﹣2018)2+(x﹣2020)2=34,求(x﹣2019)2的值.
三.完全平方式
15.若9x2﹣(K﹣1)x+1是关于x的完全平方式,则常数K的值为( )
A.0 B.﹣5或7 C.7 D.9
16.将4张长为a、宽为b(a>b)的长方形纸片按如图的方式拼成一个边长为(a+b)的正方形,图中空白部分的面积之和为S1,阴影部分的面积之和为S2,若S1=S2,则的值为 .
17.下列有四个结论:
①若(1﹣x)x+1=1,则x=﹣1;
②若a2+b2=3,a﹣b=1,则(2﹣a)(2﹣b)的值为5﹣2;
③若规定:当ab≠0时,a b=a+b﹣ab,若a (4﹣a)=0,则a=2;
④若4x=a,8y=b,则24x﹣3y可表示为;
⑤已知多项式x2+4x+m是完全平方式,则常数m=4.
其中正确的是 .(填序号)
18.先阅读下面的内容,再解决问题
例题:若m2+2mn+2n2﹣6n+9=0,求m和n的值
解:∵m2+2mn+2n2﹣6n+9=0
∴m2+2mn+n2+n2﹣6n+9=0
∴(m+n)2+(n﹣3)2=0
∴m+n=0,n﹣3=0
∴m=﹣3,n=3
问题:(1)若x2+2y2﹣2xy+4y+4=0,求y2的值;
(2)试探究关于x、y的代数式5x2+9y2﹣12xy﹣6x+2028是否有最小值,若存在,求出最小值及此时x、y的值;若不存在,说明理由
19.湘一“追逐梦想”数学兴趣小组编了一个“诗 远方”的计算程序,规定:输入数据x,y时,若输出的是代数式称为“诗S”,若输出的是等式称为“远方M”.回答下列问题:
(1)当输入正整数x,y时,得到“远方M”和“诗S”,若“远方M”为2y=x2﹣1,求证“诗S”:2(x+y+1)是完全平方式.(温馨提示:对于一个整式A,如果存在另一个整式B,使A=B2的条件,则称A是完全平方式,比如(a+b)2=a2+2ab+b2,(a﹣b)2=a2﹣2ab+b2是完全平方式.)
(2)当输入x,y时,求“远方M”:x(x﹣1)+xy+y=51的x,y的正整数解.
(3)若正数x,y互为倒数,求“诗S”:S=的最小值.
四.平方差公式
20.(3+1)×(32+1)×(34+1)×……×(332+1)+的值为 .
21.阅读下列材料:已知实数m,n满足(2m2+n2+1)(2m2+n2﹣1)=80,试求2m2+n2的值.
解:设2m2+n2=t,则原方程变为(t+1)(t﹣1)=80,整理得t2﹣1=80,即t2=81,
∴t=±9.
∵2m2+n2≥0,
∴2m2+n2=9.
上面这种方法称为“换元法”,换元法是数学学习中最常用的一种思想方法,在结构较复杂的数和式的运算中,若把其中某些部分看成一个整体,并用新字母代替(即换元),则能使复杂的问题简单化.
根据以上阅读材料内容,解决下列问题,并写出解答过程.
(1)已知实数x,y满足(2x2+2y2+3)(2x2+2y2﹣3)=27,求x2+y2的值.
(2)若四个连续正整数的积为120,求这四个连续正整数.
22.你能求(x﹣1)(x2022+x2021+x2020+…+x+1)的值吗?遇到这样的问题,我们可以先思考从简单的情形入手,先分别计算下列各式的值:
①(x﹣1)(x+1)=x2﹣1;
②(x﹣1)(x2+x+1)=x3﹣1;
③(x﹣1)(x3+x2+x+1)=x4﹣1;
…
(1)由此我们可以得到:(x﹣1)(x2022+x2021+x2020+…+x+1)= ;
(2)请你利用上面的结论,完成下面的计算:
①22022+22021+22020+…+2+1;
②(﹣2)2022+(﹣2)2021+(﹣2)2020+…+(﹣2)+1.
23.张老师在黑板上写了三个算式,希望同学们认真观察,发现规律.请你结合这些算式,解答下列问题:
请观察以下算式:
①32﹣12=8×1
②52﹣32=8×2
③72﹣52=8×3
(1)请你再写出另外两个符合上述规律的算式;
(2)验证规律:设两个连续奇数为2n+1,2n﹣1(其中n为正整数),则它们的平方差是8的倍数;
(3)拓展延伸:“两个连续偶数的平方差是8的倍数”,这个结论正确吗?
五.平方差公式的几何背景
24.【探究】如图①,从边长为a的大正方形中剪掉一个边长为b的小正方形,将阴影部分沿虚线剪开,拼成图②的长方形
(1)请你分别表示出这两个图形中阴影部分的面积
(2)比较两图的阴影部分面积,可以得到乘法公式: (用字母表示)
【应用】请应用这个公式完成下列各题
①已知4m2﹣n2=12,2m+n=4,则2m﹣n的值为
②计算:(2a+b﹣c)(2a﹣b+c)
【拓展】①(2+1)(22+1)(24+1)(28+1)…(232+1)+1结果的个位数字为
②计算:1002﹣992+982﹣972+…+42﹣32+22﹣12
参考答案
一.完全平方公式
1.解:设2021﹣x=a,x﹣2020=b,则(2021﹣x)2+(x﹣2020)2=a2+b2=2019,a+b=(2021﹣x)+(x﹣2020)=1,
所以,(2021﹣x)(x﹣2020)=ab=[(a+b)2﹣(a2+b2)]=×(12﹣2019)=﹣1009;
故选:D.
2.解:∵x+=3,
∴(x+)2=9,
即x2+=7,
∴(x2+)2=49,
∴x4+=47,
(x+)3=27,
∴x3++3(x2 + x)=27,
即x3+=18,
∴==.
故答案为:.
3.解:∵202320212+202320232﹣2,
=(20232022﹣1)2+(20232022+1)2﹣2,
=2×202320222,
∴=.
故答案为:.
4.解:(1)如图(2),大正方形的面积为一个正方形的面积与三个小长方形面积之和,
即x2+5x+6,
同时大长方形的面积也可以为(x+3)(x+2),
所以x2+5x+6=(x+3)(x+2);
故答案为:x2+5x+6=(x+3)(x+2);
(2)如图(3),Rt△ABC中,∠C=90°,CA=3,CB=4,AB=5,
∵S△ABC=AC BC=AB CH,
∴CH===;
答:CH的长为;
(3)证明:如图(4),
∵OM⊥AB,ON⊥AC,CH⊥AB,垂足分别为点M,N,H,
∴S△ABC=S△ABO+S△AOC,
∴AB CH=AB OM+AC ON,
∵AB=AC,
∴CH=OM+ON.
即OM+ON=CH.
5.解:(1)∵a2+b2=10,a+b=4.
∴(a+b)2=a2+b2+2ab.
∴2ab=16﹣10=6.
∴(a﹣b)2=a2+b2﹣2ab=4.
∴a﹣b=±2.
(2)∵(ax﹣3)(2x+1)﹣2x2+m
=2ax2+ax﹣6x﹣3﹣2x2+m
=(2a﹣2)x2+(a﹣6)x+m﹣3.
∵不含x2项与常数项.
∴2a﹣2=0,m﹣3=0.
∴a=1,m=3.
∵an2+mn=1.
∴n2+3n=1.
∴2n3+5n2﹣5n+2022=2n3+6n2﹣n2﹣5n+2022.
=2n(n2+3n)﹣n2﹣5n+2022
=2n﹣n2﹣5n+2022
=﹣(n2+3n)+2022
=﹣1+2022
=2021.
6.解:第n个式子:n2+[n(n+1)]2+(n+1)2=[n(n+1)+1]2,
证明:因为左边=n2+[n(n+1)]2+(n+1)2,
=n2+(n2+n)2+(n+1)2,
=(n2+n)2+2n2+2n+1,
=(n2+n)2+2(n2+n)+1,
=(n2+n+1)2,
而右边=(n2+n+1)2,
所以,左边=右边,等式成立.
二.完全平方公式的几何背景(共8小题)
7.解:设AB=x,AD=y,
∵正方形ABEF和ADGH的面积之和为17cm2
∴x2+y2=17,
∵矩形ABCD的周长是10cm
∴2(x+y)=10,
∵(x+y)2=x2+2xy+y2,
∴25=17+2xy,
∴xy=4,
∴矩形ABCD的面积为:xy=4cm2,
故选:B.
8.解:∵S1=(a+2b)2﹣b2﹣a(a+2b)﹣b2﹣(a+b)2=2ab+b2,S2=b2,S1=6S2,
∴2ab+b2=6b2,
∴.
故答案为:.
9.解:(1)阴影部分的正方形边长为a﹣b,故周长为4(a﹣b)=4a﹣4b,
故答案为:4a﹣4b;
(2)大正方形面积可以看作四个矩形面积加阴影面积,故可表示为:4ab+(a﹣b) ,
大正方形边长为a+b,故面积也可以表达为:(a+b) ,
因此(a+b) =(a﹣b) +4ab,
故答案为:(a+b) =(a﹣b) +4ab;
(3)由(2)可知:(m+n) =(m﹣n) +4mn,
已知m﹣n=4,mn=﹣3,
所以(m+n) =16+4×(﹣3)=4,
所以m+n=±2;
故m+n的值为±2;
(4)设AC=a,BC=b,
因为AB=8,S1+S2=26,
所以a+b=8,a +b =26,
因为(a+b) =a +b +2ab,
所以64=26+2ab,解得ab=19,
由题意:∠ACF=90°,
所以S阴影=ab=.
10.解:(1)由图①和图②中矩形的面积为等量得:
4ab=(a+b)2﹣(a﹣b)2,
故答案为:4ab=(a+b)2﹣(a﹣b)2;
(2)由(1)中公式可得:(a﹣b)2=(a+b)2﹣4ab.
同理可得:
(x﹣y)2=(x+y)2﹣4xy
=
=7,
故答案为:7;
(3)分别以大矩形的面积和几个小矩形的面积为等量可得:
(3a+b)(a+b)=3a2+4ab+b2,
故答案为:(3a+b)(a+b)=3a2+4ab+b2;
(4)在正方形ACDE和正方形BCGF中,
∠ECD=∠CGB=45°,
∴EC∥BG,
∴S△BGE=S△BGC.
当BC=1时,,
当BC=2时,,
……
当BC=n时,,
∴S2021﹣S2020
=
=
=.
11.解:(1)∵大正方形的面积为36,小正方形的面积为4,
∴(x+y)2=36,(x﹣y)2=4,
又∵x>y>0,
∴x+y=6,x﹣y=2,
故答案为:2,6;
(2)大正方形的边长为x+y=9﹣m+m﹣4=5,
∵(9﹣m)(m﹣4)=4,
∴(9﹣m)2+(m﹣4)2=[(9﹣m)+(m﹣4)]2﹣2(9﹣m)(m﹣4)=52﹣8=17,
故答案为:5,17;
(3)a,b,c三边的数量关系为a2+b2=c2.理由如下:
由拼图可得,小正方形的边长为a﹣b,
由大正方形的面积等于小正方形的面积与4个直角三角形的面积和可得,
(a﹣b)2+ab×4=c2,
即a2+b2=c2.
12.解:(1)方法1:图2是边长为(a+b)的正方形,
∴S正方形=(a+b)2;
方法2:图2可看成1个边长为a的正方形、1个边长为b的正方形以及2个长为b宽为a的长方形的组合体,
∴S正方形=a2+b2+2ab.
故答案为:(a+b)2;a2+b2+2ab;
(2)由(1)可得:(a+b)2=a2+2ab+b2.
故答案为:(a+b)2=a2+2ab+b2
(3)①∵a+b=5,
∴(a+b)2=25,
∴a2+b2+2ab=25,
又∵a2+b2=13,
∴ab=6;
②设2020﹣a=x,a﹣2019=y,则x+y=1,
∵(2020﹣a)2+(a﹣2019)2=5,
∴x2+y2=5,
∵(x+y)2=x2+2xy+y2,
∴xy===﹣2,
即(2020﹣a)(a﹣2019)=xy=﹣2;
③设a﹣2019=x,a﹣2021=y,则x﹣y=2,
∵(a﹣2019)2+(a﹣2021)2=8,
∴x2+y2=8,
∵(x﹣y)2=x2﹣2xy+y2,
∴xy=,
∵x﹣y=2,即y=x﹣2,
∴(a﹣2020)2=(a﹣2000)(a﹣2000)=(x﹣1)(y+1)=xy+x﹣y﹣1=3.
13.解:(1)设正方形A,B的边长分别为a,b(a>b),
由图甲得(a﹣b)2=1,由图乙得(a+b)2﹣a2﹣b2=12
得ab=6,a2+b2=13,
故答案为:13;
(2)∵ab=6,a2+b2=13,
∴(a+b)2=(a﹣b)2+4ab=1+24=25,
∵a+b>0,
∴a+b=5,
∵(a﹣b)2=1,
∴a﹣b=1,
∴图丙的阴影部分面积S=(2a+b)2﹣3a2﹣2b2=a2﹣b2+4ab=(a﹣b)(a+b)+4ab=5+24=29.
14.解:(1)图2是边长为(a+b)的正方形,因此面积为(a+b)2,
图2可以看作4个部分的面积和,即为a2+2ab+b2,
故答案为:(a+b)2,a2+2ab+b2;
(2)由(1)的两种方法计算图形的面积可得,(a+b)2=a2+2ab+b2;
(3)如图,可以验证:(a+b)(a+2b)=a2+3ab+2b2;
(4)①∵a+b=6,a2+b2=14,
∴2ab=(a+b)2﹣(a2+b2)=36﹣14=22,
即ab=11,
②设a=x﹣2018,b=x﹣2020,则a﹣b=2,a2+b2=34,=x﹣2019,
∴2ab=(a2+b2)﹣(a﹣b)2=34﹣4=30,
∴(x﹣2019)2=()2===16,
答:(x﹣2019)2的值为16.
三.完全平方式
15.解:9x2﹣(K﹣1)x+1=(3x)2﹣(K﹣1)x+12.
∵9x2﹣(K﹣1)x+1是关于x的完全平方式,
∴9x2﹣(K﹣1)x+1=(3x)2±2 3x 1+12=(3x)2±6x+12.
∴﹣(K﹣1)=±6.
当﹣(K﹣1)=6时,K=﹣5.
当﹣(K﹣1)=﹣6时,K=7.
综上:K=﹣5或7.
故选:B.
16.解:S1=4×ab+(a﹣b)2
=2ab+a2﹣2ab+b2
=a2+b2,
S2=()2﹣(a﹣b)2
=a2+b2﹣a2+2ab﹣b2
=2ab,
∵S1=S2,
∴a2+b2= 2ab,
∴3a2﹣10ab+3b2=0,
(3a﹣b)(a﹣3b)=0,
∴3a﹣b=0或a﹣3b=0,
解得:a=b或a=3b,
∵a>b>0,
∴a=b舍去,
当a=3b时,==3,
故答案为:3.
17.解:①可以分为三种情况:
当x+1=0时,x=﹣1;
当1﹣x=1时,x=0;
当1﹣x=﹣1,x+1为偶数时,x=2,但x+1=3不是偶数,舍去;
综上所述,x=﹣1或0.
∴①不符合题意;
②(2﹣a)(2﹣b)
=4﹣2b﹣2a+ab
=4﹣2(a+b)+ab,
∵a﹣b=1,
∴(a﹣b)2=1,
∴a2+b2﹣2ab=1,
∴ab=1,
∴(a+b)2=a2+b2+2ab=3+2=5,
∴a+b=±,
当a+b=时,原式=4﹣2+1=5﹣2;
当a+b=﹣时,原式=4+2+1=5+2,
∴a+b=5±2.
∴②不符合题意;
③根据定义得:a+4﹣a+a(4﹣a)=0,
解得:a=2,
∴③符合题意;
④∵4x=(22)x=22x,8y=(23)y=23y,
∴24x﹣3y===,
∴④不符合题意;
⑤∵x2+4x+m是完全平方式,
∴m=()2=4,
∴⑤符合题意,
故答案为:③⑤.
18.解:(1)∵x2+2y2﹣2xy+4y+4=0,
∴(x﹣y)2+(y+2)2=0,
∴x﹣y=0,y+2=0,
x=y=﹣2.
∴y2=(﹣2)2=4;
(2)∵5x2+9y2﹣12xy﹣6x+2028
=(4x2+9y2﹣12xy)+(x2﹣6x+9)+2019
=(2x﹣3y)2+(x﹣3)2+2019.
∵(2x﹣3y)2≥0,(x﹣3)2≥0,
∴(2x﹣3y)2+(x﹣3)2+2019≥2019.
∴当2x﹣3y=0,x﹣3=0时,即当x=3,y=2时,代数式5x2+9y2﹣12xy﹣6x+2028有最小值2019.
19.解:2y=x2﹣1代入2(x+y+1),得
2(x+y+1)
=2x+2y+2
=2x+x2﹣1+2
=x2+2x+1
=(x+1)2
为完全平方式.
(2)∵x(x﹣1)+xy+y=51
∴x2﹣x﹣2+xy+y=49
(x+1)(x﹣2)+y(x+1)=49
(x+1)(x+y﹣2)=49
∵x,y都是正整数,
∴或或
解得或(舍去)或(舍去),
∴x,y的正整数解为6和3;
(3)∵正数x,y互为倒数,
∴xy=1
S=
=
=1﹣
当x+2y取最小值时,S有最小值,
∵x+2y≥2=2
即x=,y=
S=1﹣
=1+2﹣3
=2﹣2.
答:“诗S”:S=的最小值为2﹣2.
四.平方差公式
20.解:原式=(3﹣1)×(3+1)×(32+1)×(34+1)×……×(332+1)+
=(32﹣1)×(32+1)×(34+1)×……×(332+1)+
=(34﹣1)×(34+1)×……×(332+1)+
=(38﹣1)×……×(332+1)+
=(364﹣1)+
=﹣+
=.
21.解:(1)设2x2+2y2=m,则(m+3)(m﹣3)=27,
∴m2﹣9=27,即m2=36,∴m=±6,
∵2x2+2y2≥0,∴2x2+2y2=6,
∴x2+y2=3;
(2)设最小数为x,则x(x+1)(x+2)(x+3)=120,
即:(x2+3x)(x2+3x+2)=120,
设x2+3x=y,则y2+2y﹣120=0,
∴y1=﹣12,y2=10,
∵x为正整数,
∴y=x2+3x=10,
∴x1=2,x2=﹣5<0(舍去),
∴这四个整数为2,3,4,5.
22.解:(1)根据规律,原式=x2023﹣1,
故答案为:x2023﹣1;
(2)①规律用字母表示为:(x﹣1)(xn+xn﹣1+...+x+1)=xn+1﹣1,
当x=2,n=2022时,
(2﹣1)(22022+22021+22020+...+2+1)=22023﹣1,
∴22022+22021+22020+...+2+1=22023﹣1;
②当x=﹣2,n=2022时,
(﹣2﹣1)[(﹣2)2022+(﹣2)2021+(﹣2)2020+...+(﹣2)+1]=(﹣2)2023﹣1,
∴(﹣2)2022+(﹣2)2021+(﹣2)2020+...+(﹣2)+1=.
23.解:(1)92﹣72=8×4,112﹣92=8×5;
(2)验证规律:设两个连续奇数为2n+1,2n﹣1(其中n为正整数),
则它们的平方差是8的倍数;
(2n+1)2﹣(2n﹣1)2=(2n+1﹣2n+1)(2n+1+2n﹣1)=2×4n=8n
故两个连续奇数的平方差是8的倍数.
(3)拓展延伸:“两个连续偶数的平方差是8的倍数”,这个结论正确吗?
不正确.
解法一:举反例:42﹣22=12,
因为12不是8的倍数,故这个结论不正确.
解法二:设这两个偶数为2n和2n+2,(2n+2)2﹣(2n)2=(2n+2﹣2n)(2n+2+2n)=8n+4
因为8n+4不是8的倍数,故这个结论不正确.
五.平方差公式的几何背景
24.解:(1)图①按照正方形面积公式可得:a2﹣b2;
图②按照长方形面积公式可得:(a+b)(a﹣b).
故答案为:a2﹣b2;(a+b)(a﹣b).
(2)令(1)中两式相等可得:(a+b)(a﹣b)=a2﹣b2
故答案为:(a+b)(a﹣b)=a2﹣b2.
【应用】①∵4m2﹣n2=12,2m+n=4,4m2﹣n2=(2m+n)(2m﹣n)
∴(2m﹣n)=12÷4=3
故答案为:3.
②(2a+b﹣c)(2a﹣b+c)
=[2a+(b﹣c)][2a﹣(b﹣c)]
=4a2﹣(b﹣c)2
=4a2﹣b2+2bc﹣c2
【拓展】①
原式=(2﹣1)(2+1)(22+1)(24+1)(28+1)…(232+1)+1
=(22﹣1)(22+1)(24+1)(28+1)…(232+1)+1
=(24﹣1)(24+1)(28+1)…(232+1)+1
=(28﹣1)(28+1)…(232+1)+1
=(216﹣1)…(232+1)+1
=264﹣1+1
=264
∵2的正整数次方的尾数为2,4,8,6循环,64÷4=16
故答案为:6.
②原式=(100+99)(100﹣99)+(98+97)(98﹣97)+…+(4+3)(4﹣3)+(2+1)(2﹣1)
=100+99+98+97+…+4+3+2+1
=5050
