2021-2022学年人教版八年级数学上册15.2分式的运算辅导训练(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版八年级数学上册15.2分式的运算辅导训练(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 268.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-29 14:24:53 | ||
图片预览




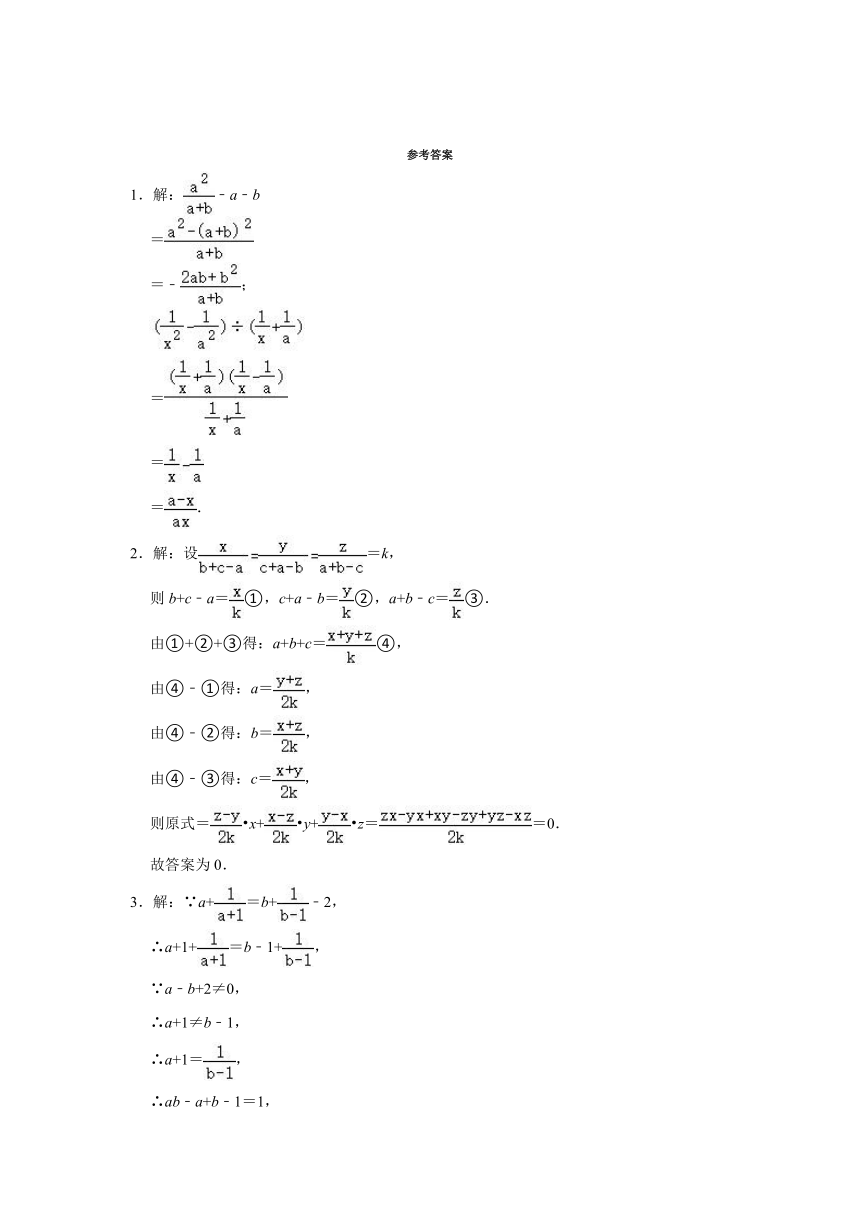
文档简介
2021-2022学年人教版八年级数学上册《15.2分式的运算》优生辅导训练(附答案)
1.计算:﹣a﹣b= ,= .
2.已知:,则(b﹣c)x+(c﹣a)y+(a﹣b)z的值为 .
3.已知a+=b+﹣2,且a﹣b+2≠0,则ab﹣a+b= .
4.已知实数a、b、c满足a+b=ab=c,有下列结论:
①若c≠0,则+=1;
②若a=3,则b+c=9;
③若a、b、c中只有两个数相等,则a+b+c=8.
其中正确的是 . (把所有正确结论的序号都填上)
5.(1)已知,则= ;
(2)已知,则= .
6.已知abc≠0,且,则的值是 或 .
7.计算:
(1);
(2).
8.计算:
(1)
(2)
(3)
(4).
9.计算:
(1);
(2);
(3);
(4).
10.某快递公司有甲、乙、丙三个机器人分配快件,甲单独完成需要x小时,乙单独完成需要y小时,丙单独完成需要z小时.
(1)求甲单独完成的时间是乙丙合作完成时间的几倍?
(2)若甲单独完成的时间是乙丙合作完成时间的a倍,乙单独完成的时间是甲丙合作完成时间的b倍,丙单独完成的时间是甲乙合作完成时间的c倍,求的值.
11.已知=++,试求A+B+2C的值.
12.化简:(﹣)÷
13.化简:(+)×.
14.(1)已知(a+b)2=6,(a﹣b)2=2,求a2+b2与ab的值;
(2)已知x+,求x2的值
15.先化简后求值:已知:x=﹣2,求分式1﹣的值.
16.先化简,再求值: ﹣,其中a=.
17.已知小丽和小颖购买同一种商品的平均价格分别为元/千克和元/千克(a,b是正数,且a≠b),请比较小丽和小颖所购买商品的平均价格的高低.
18.甲工程队完成一项工程需要n天(n>1),乙工程队完成这项工程的时间是甲工程队的2倍多1天,则甲队的工作效率是乙队的3倍吗?请说明理由.
19.阅读下面材料,并解答问题.
材料:将分式拆分成一个整式与一个分式(分子为整数)的和的形式.
解:由分母为﹣x2+1,可设﹣x4﹣x2+3=(﹣x2+1)(x2+a)+b
则﹣x4﹣x2+3=(﹣x2+1)(x2+a)+b=﹣x4﹣ax2+x2+a+b=﹣x4﹣(a﹣1)x2+(a+b)
∵对应任意x,上述等式均成立,∴,∴a=2,b=1.
∴=+.
这样,分式被拆分成了一个整式(x2+2)与一个分式的和.
解答:
(1)将分式拆分成一个整式与一个分式(分子为整数)的和的形式.
(2)当﹣1<x<1时,试求的最小值.
(3)如果的值为整数,求x的整数值.
20.分式中,在分子、分母都是整式的情况下,如果分子的次数低于分母的次数,称这样的分式为真分式,例如:分式,是真分式.如果分子的次数不低于分母的次数,称这样的分式为假分式.例如,分式,是假分式,一个假分式可以化为一个整式与一个真分式的和.
例如:==1+
(1)将假分式化为一个整数与一个真分式的和;
(2)利用上述方法解决问题:若x是整数,且分式的值为正整数,求x的值.
21.阅读理解:
【例】已知x+=3,求分式的值.
解:因为﹣4=3﹣4=﹣1,所以=﹣1.
【活学活用】
(1)已知a+=﹣5,求分式的值.
(2)已知b+=﹣3,求分式的值.
(3)已知x+=﹣5,求分式的值.
参考答案
1.解:﹣a﹣b
=
=﹣;
=
=
=.
2.解:设=k,
则b+c﹣a=①,c+a﹣b=②,a+b﹣c=③.
由①+②+③得:a+b+c=④,
由④﹣①得:a=,
由④﹣②得:b=,
由④﹣③得:c=,
则原式= x+ y+ z==0.
故答案为0.
3.解:∵a+=b+﹣2,
∴a+1+=b﹣1+,
∵a﹣b+2≠0,
∴a+1≠b﹣1,
∴a+1=,
∴ab﹣a+b﹣1=1,
∴ab﹣a+b=2
故答案为2.
4.解:∵c≠0,a+b=ab=c,
∴ab≠0,
∴=1,
∴+=1,故①正确.
∵a=3,a+b=ab=c,
∴3+b=3b=c,
∴b=,c=,
∴b+c=+=6,故②错误,
∵a、b、c中只有两个数相等,
假设a=b,则有2a=a2=c,
∴a=2或0(舍弃),
∴a=b=2,c=4,
∴a+b+c=8,
假设a=c,则有b+c=bc=c,则a=b=c=0,不合题意,同理b=c也不合题意,故③正确,
故答案为①③.
5.解:(1)由=2,得到1+3 =2,
则=;
(2)由﹣=5,得到=5,即a﹣b=﹣5ab,
则原式===,
故答案为:(1);(2).
6.解:∵=,
∴b(a+b﹣c)=c(a﹣b+c),
∴ab+b2﹣bc﹣ac+bc﹣c2=0,
∴(b﹣c)(a+b+c)=0,
∴b=c或a+b=﹣c,
同理:a=b或b+c=﹣a,
a=c或a+c=﹣b,
当b=c,a=b,a=c时,
原式==8;
当a+b=﹣c,b+c=﹣a,a+c=﹣b时,
原式==﹣1.
故答案为:8或﹣1.
7.解:(1)原式=﹣;
(2)原式=
=.
8.解:(1)原式= =;
(2)原式= (﹣ )=﹣a5;
(3)原式= (a+b)(a﹣b)=;
(4)原式=﹣ =﹣.
9.解:(1)原式= =;
(2)原式=144x8y2÷(﹣27 )=﹣x2y5;
(3)原式=﹣(a﹣5) =﹣(a+5)=﹣a﹣5;
(4)原式= =.
10.解:(1)x÷[1÷(+)]
=x÷[1÷]
=x÷
=.
答:甲单独完成的时间是乙丙合作完成时间的倍;
(2)由题意得x=①,y=②,z=③.
由①得a=+,
∴a+1=++1,
∴==;
同理,由②得=;
由③得=;
∴=++==1.
11.解:∵=++
∴=
∴=
∴
∴A=1,B=﹣3,C=3
∴A+B+2C=4.
12.解:原式=
=
=
13.解:原式=
=
=
=﹣2.
14.解:(1)∵(a+b)2=6,(a﹣b)2=2,
∴a2+2ab+b2=6 ①,
a2﹣2ab+b2=2 ②,
①+②,得:2(a2+b2)=8,
则a2+b2=4;
①﹣②,得:4ab=4,
则ab=1;
(2)∵x+,
∴x2=(x+)2﹣2=9﹣2=7.
15.解:原式=1﹣ (÷)
=1﹣
=1﹣
=,
当x=﹣2时,
原式===.
16.解: ﹣
=
=
=
=,
当a=时,原式=﹣=﹣3.
17.解:∵a,b是正数,且a≠b,
∴﹣==>0,
∴>,
则小丽的价格高,小颖的价格低.
18.解:甲队的工作效率不是乙队的3倍.
甲的工作效率:,
乙的工作效率:,
甲队的工作效率是乙队的÷=(倍),
∵n>1,
∴<3,
∴甲队的工作效率不是乙队的3倍.
19.解:(1)由分母为﹣x2+1,可设﹣x4﹣6x2+8=(﹣x2+1)(x2+a)+b,
则﹣x4﹣6x2+8=(﹣x2+1)(x2+a)+b=﹣x4﹣ax2+x2+a+b=﹣x4﹣(a﹣1)x2+(a+b),
∵对应任意x,上述等式均成立,
∴,
∴a=7,b=1,
∴==+=x2+7+,
这样,分式被拆分成了一个整式x2+7与一个分式的和.
(2)=x2+7+,
∵x2≥0,
∴x2+7≥7,
此时﹣1<x<1,
当x=0时,取得最小值0,
∴当x=0时,x2+7+最小值为8,
即的最小值为8.
(3)===2﹣;
∵的值为整数,且x为整数;
∴x+1为3的约数,
∴x+1的值为1或﹣1或3或﹣3;
∴x的值为0或﹣2或2或﹣4.
20.解:(1)==2﹣
(2)∵==+=x+3+
∵分式的值为正整数
∴x2>0,x﹣3>0
∴x﹣3=1或x﹣3=3或x﹣3=9
∴x=4或x=6或x=12
21.解:(1)∵a+=﹣5,
∴
=2a+5+
=2(a+)+5
=2×(﹣5)+5
=﹣5;
(2)∵b+=﹣3,
∴
=3b﹣4+
=3(b+)﹣4
=3×(﹣3)﹣4
=﹣13,
∴=﹣;
(3)∵x+=﹣5,
∴
=
=x+1﹣3+
=x+﹣2
=﹣5﹣2
=﹣7,
∴.
1.计算:﹣a﹣b= ,= .
2.已知:,则(b﹣c)x+(c﹣a)y+(a﹣b)z的值为 .
3.已知a+=b+﹣2,且a﹣b+2≠0,则ab﹣a+b= .
4.已知实数a、b、c满足a+b=ab=c,有下列结论:
①若c≠0,则+=1;
②若a=3,则b+c=9;
③若a、b、c中只有两个数相等,则a+b+c=8.
其中正确的是 . (把所有正确结论的序号都填上)
5.(1)已知,则= ;
(2)已知,则= .
6.已知abc≠0,且,则的值是 或 .
7.计算:
(1);
(2).
8.计算:
(1)
(2)
(3)
(4).
9.计算:
(1);
(2);
(3);
(4).
10.某快递公司有甲、乙、丙三个机器人分配快件,甲单独完成需要x小时,乙单独完成需要y小时,丙单独完成需要z小时.
(1)求甲单独完成的时间是乙丙合作完成时间的几倍?
(2)若甲单独完成的时间是乙丙合作完成时间的a倍,乙单独完成的时间是甲丙合作完成时间的b倍,丙单独完成的时间是甲乙合作完成时间的c倍,求的值.
11.已知=++,试求A+B+2C的值.
12.化简:(﹣)÷
13.化简:(+)×.
14.(1)已知(a+b)2=6,(a﹣b)2=2,求a2+b2与ab的值;
(2)已知x+,求x2的值
15.先化简后求值:已知:x=﹣2,求分式1﹣的值.
16.先化简,再求值: ﹣,其中a=.
17.已知小丽和小颖购买同一种商品的平均价格分别为元/千克和元/千克(a,b是正数,且a≠b),请比较小丽和小颖所购买商品的平均价格的高低.
18.甲工程队完成一项工程需要n天(n>1),乙工程队完成这项工程的时间是甲工程队的2倍多1天,则甲队的工作效率是乙队的3倍吗?请说明理由.
19.阅读下面材料,并解答问题.
材料:将分式拆分成一个整式与一个分式(分子为整数)的和的形式.
解:由分母为﹣x2+1,可设﹣x4﹣x2+3=(﹣x2+1)(x2+a)+b
则﹣x4﹣x2+3=(﹣x2+1)(x2+a)+b=﹣x4﹣ax2+x2+a+b=﹣x4﹣(a﹣1)x2+(a+b)
∵对应任意x,上述等式均成立,∴,∴a=2,b=1.
∴=+.
这样,分式被拆分成了一个整式(x2+2)与一个分式的和.
解答:
(1)将分式拆分成一个整式与一个分式(分子为整数)的和的形式.
(2)当﹣1<x<1时,试求的最小值.
(3)如果的值为整数,求x的整数值.
20.分式中,在分子、分母都是整式的情况下,如果分子的次数低于分母的次数,称这样的分式为真分式,例如:分式,是真分式.如果分子的次数不低于分母的次数,称这样的分式为假分式.例如,分式,是假分式,一个假分式可以化为一个整式与一个真分式的和.
例如:==1+
(1)将假分式化为一个整数与一个真分式的和;
(2)利用上述方法解决问题:若x是整数,且分式的值为正整数,求x的值.
21.阅读理解:
【例】已知x+=3,求分式的值.
解:因为﹣4=3﹣4=﹣1,所以=﹣1.
【活学活用】
(1)已知a+=﹣5,求分式的值.
(2)已知b+=﹣3,求分式的值.
(3)已知x+=﹣5,求分式的值.
参考答案
1.解:﹣a﹣b
=
=﹣;
=
=
=.
2.解:设=k,
则b+c﹣a=①,c+a﹣b=②,a+b﹣c=③.
由①+②+③得:a+b+c=④,
由④﹣①得:a=,
由④﹣②得:b=,
由④﹣③得:c=,
则原式= x+ y+ z==0.
故答案为0.
3.解:∵a+=b+﹣2,
∴a+1+=b﹣1+,
∵a﹣b+2≠0,
∴a+1≠b﹣1,
∴a+1=,
∴ab﹣a+b﹣1=1,
∴ab﹣a+b=2
故答案为2.
4.解:∵c≠0,a+b=ab=c,
∴ab≠0,
∴=1,
∴+=1,故①正确.
∵a=3,a+b=ab=c,
∴3+b=3b=c,
∴b=,c=,
∴b+c=+=6,故②错误,
∵a、b、c中只有两个数相等,
假设a=b,则有2a=a2=c,
∴a=2或0(舍弃),
∴a=b=2,c=4,
∴a+b+c=8,
假设a=c,则有b+c=bc=c,则a=b=c=0,不合题意,同理b=c也不合题意,故③正确,
故答案为①③.
5.解:(1)由=2,得到1+3 =2,
则=;
(2)由﹣=5,得到=5,即a﹣b=﹣5ab,
则原式===,
故答案为:(1);(2).
6.解:∵=,
∴b(a+b﹣c)=c(a﹣b+c),
∴ab+b2﹣bc﹣ac+bc﹣c2=0,
∴(b﹣c)(a+b+c)=0,
∴b=c或a+b=﹣c,
同理:a=b或b+c=﹣a,
a=c或a+c=﹣b,
当b=c,a=b,a=c时,
原式==8;
当a+b=﹣c,b+c=﹣a,a+c=﹣b时,
原式==﹣1.
故答案为:8或﹣1.
7.解:(1)原式=﹣;
(2)原式=
=.
8.解:(1)原式= =;
(2)原式= (﹣ )=﹣a5;
(3)原式= (a+b)(a﹣b)=;
(4)原式=﹣ =﹣.
9.解:(1)原式= =;
(2)原式=144x8y2÷(﹣27 )=﹣x2y5;
(3)原式=﹣(a﹣5) =﹣(a+5)=﹣a﹣5;
(4)原式= =.
10.解:(1)x÷[1÷(+)]
=x÷[1÷]
=x÷
=.
答:甲单独完成的时间是乙丙合作完成时间的倍;
(2)由题意得x=①,y=②,z=③.
由①得a=+,
∴a+1=++1,
∴==;
同理,由②得=;
由③得=;
∴=++==1.
11.解:∵=++
∴=
∴=
∴
∴A=1,B=﹣3,C=3
∴A+B+2C=4.
12.解:原式=
=
=
13.解:原式=
=
=
=﹣2.
14.解:(1)∵(a+b)2=6,(a﹣b)2=2,
∴a2+2ab+b2=6 ①,
a2﹣2ab+b2=2 ②,
①+②,得:2(a2+b2)=8,
则a2+b2=4;
①﹣②,得:4ab=4,
则ab=1;
(2)∵x+,
∴x2=(x+)2﹣2=9﹣2=7.
15.解:原式=1﹣ (÷)
=1﹣
=1﹣
=,
当x=﹣2时,
原式===.
16.解: ﹣
=
=
=
=,
当a=时,原式=﹣=﹣3.
17.解:∵a,b是正数,且a≠b,
∴﹣==>0,
∴>,
则小丽的价格高,小颖的价格低.
18.解:甲队的工作效率不是乙队的3倍.
甲的工作效率:,
乙的工作效率:,
甲队的工作效率是乙队的÷=(倍),
∵n>1,
∴<3,
∴甲队的工作效率不是乙队的3倍.
19.解:(1)由分母为﹣x2+1,可设﹣x4﹣6x2+8=(﹣x2+1)(x2+a)+b,
则﹣x4﹣6x2+8=(﹣x2+1)(x2+a)+b=﹣x4﹣ax2+x2+a+b=﹣x4﹣(a﹣1)x2+(a+b),
∵对应任意x,上述等式均成立,
∴,
∴a=7,b=1,
∴==+=x2+7+,
这样,分式被拆分成了一个整式x2+7与一个分式的和.
(2)=x2+7+,
∵x2≥0,
∴x2+7≥7,
此时﹣1<x<1,
当x=0时,取得最小值0,
∴当x=0时,x2+7+最小值为8,
即的最小值为8.
(3)===2﹣;
∵的值为整数,且x为整数;
∴x+1为3的约数,
∴x+1的值为1或﹣1或3或﹣3;
∴x的值为0或﹣2或2或﹣4.
20.解:(1)==2﹣
(2)∵==+=x+3+
∵分式的值为正整数
∴x2>0,x﹣3>0
∴x﹣3=1或x﹣3=3或x﹣3=9
∴x=4或x=6或x=12
21.解:(1)∵a+=﹣5,
∴
=2a+5+
=2(a+)+5
=2×(﹣5)+5
=﹣5;
(2)∵b+=﹣3,
∴
=3b﹣4+
=3(b+)﹣4
=3×(﹣3)﹣4
=﹣13,
∴=﹣;
(3)∵x+=﹣5,
∴
=
=x+1﹣3+
=x+﹣2
=﹣5﹣2
=﹣7,
∴.
