2021—2022学年华东师大版数学九年级上册24.3.1 锐角三角函数 课件(共23张PPT)
文档属性
| 名称 | 2021—2022学年华东师大版数学九年级上册24.3.1 锐角三角函数 课件(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-28 20:27:09 | ||
图片预览







文档简介
(共23张PPT)
一、教学目标
知识技能目标:1.了解三角函数的概念,学会在直角三角形中进行一些简单的计算。
2.知道30°、45°、60°角的三角函数值;会使用计算器由已知锐角求它的三角函数值, 由已知三角函数值求它对应的锐角。
3.理解并掌握直角三角形边角之间的关系
过程方法目标:
(1)通过体验三角函数概念的形成过程增进学生的数学经验
(2)渗透数形结合的数学思想方法
(3)培养学生主动探索,敢于实践,勇于发现,合作交流的精神。
情感态度目标:
(1)让学生感受数学来源于生活又应用于生活,体验数学的生活化经历。
(2)通过实际问题情境的经历探究性的学习培养学生学习数学的兴趣,培养学生热爱数学、热爱生活的情感。
二、教学重点:
锐角三角函数的概念及其简单的计算
三、教学难点:
三角函数概念的形成
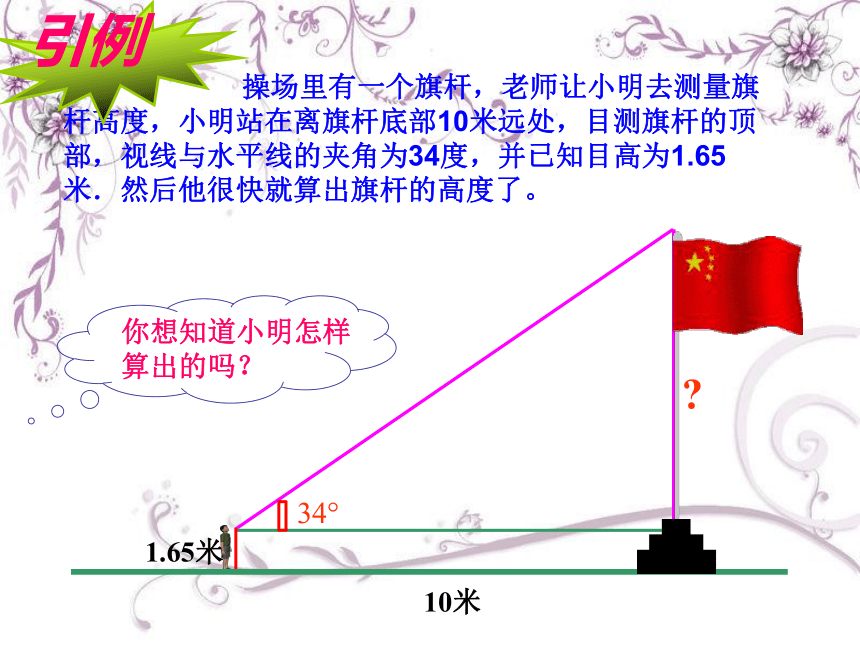
操场里有一个旗杆,老师让小明去测量旗杆高度,小明站在离旗杆底部10米远处,目测旗杆的顶部,视线与水平线的夹角为34度,并已知目高为1.65米.然后他很快就算出旗杆的高度了。
1.65米
10米
你想知道小明怎样算出的吗?
引例
∠A的对边 a
∠A的邻边 b
直角三角形ABC可以简记为Rt△ABC
直角∠C所对的边AB称为斜边,用c表示
另两条直角边分别叫∠A的对边与邻边,用a、b表示.
A
B
C
斜边 C
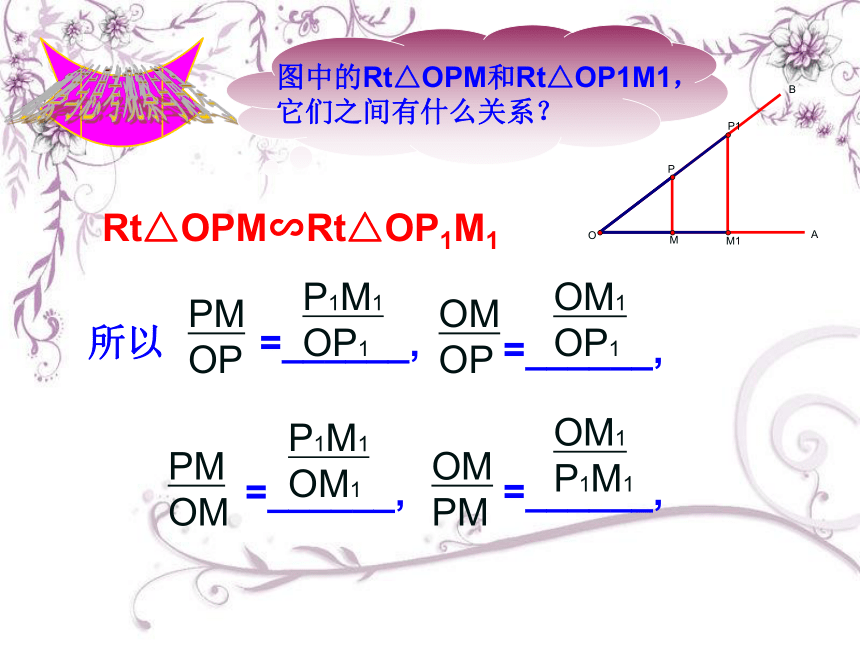
Rt△OPM∽Rt△OP1M1
P1M1
OP1
PM
OP
所以
OM
OP
OM1
OP1
PM
OM
OM
PM
P1M1
OM1
=______,
=______,
=______,
OM1
P1M1
=______,
B
A
M1
M
O
P
P1
图中的Rt△OPM和Rt△OP1M1,它们之间有什么关系?
在Rt△ABC中,对于锐角A的每一个确定的值,
①∠A的对边与斜边的比值与△ABC的边长大小有关系吗?
②∠A的邻边与斜边的比值呢?
③∠A的对边与邻边的比值呢?
在Rt△ABC中,对于锐角A的每一个确定的值,其对边与斜边、邻边与斜边、对边与邻边的比值是惟一确定的.
由此可见
这几个比值都是锐角∠A的函数,记作sin A、cosA、tan A,即
sin A=
cosA=
tan A=
分别叫做锐角∠A的正弦、余弦、正切,统称为锐角∠A的三角函数.
方法指导:
(1)我们现阶段所研究的锐角三角函数都是在直角三角形中定义的;
(2) sinA ,cosA、 tanA 都是表达符号,它们是一个整体,不能拆开来理解:
(3) sinA , cosA、 tanA 中 ∠A 的角的记号“ ∠ ”习惯上省略不写 ,但对于用三个字母和阿拉伯数字表示的角,角的记号“∠”不能省略,例如 sin∠1不能写成 sin1 .
0﹤ sin A﹤1, 0﹤ cos A﹤1 为什么
根据三角函数定义,我们还可以得出
你能够证明这两个公式吗?试试看
显然
求出如图所示的Rt△ABC中∠A的三角函数值.
∵
∴ sinA =
cosA =
tanA =
解
例 1
变式练习:
1.下图中∠ACB=90° ,CD⊥AB
指出∠A的对边、邻边。
A
B
C
D
2.上题中如果CD=5,AC=10,
则sin∠ACD=________
sin ∠DCB=________
3(1)在△ABC中,∠B=90 ,BC=3,AB=4,
则tanA=_____ cosA=______
(2)tan20 ·tan(90 -∠A)=1,则锐角∠A=_____
例 2
【点评】本题主要考查了三角函数的定义,正确求出图形中的线段的长是解决本题的关键.
因而可以设CD=3x,AD=5x,
根据勾股定理得到AC=4x,则BC=AD=5x,
∵BD=4,∴5x﹣3x=4,
解得x=2,
因而BC=10,AC=8,
CD=6;
如图,在△ABC中∠C=90°,点D在BC上,BD=4,AD=BC,
求:(1)DC的长;(2)sinB的值.
变式练习:
∴AC=4,
∴BC=CD+DB=3+5=8,
4.如图,在Rt△ABC中,∠C=90°,点D在边BC上,AD=BD=5,
【点评】本题考查了直角三角形中正弦值的计算,考查了勾股定理的运用,本题中求AC的长是解题的关键.
变式练习
【解答】解:∵CD⊥AB,∠ACB=90°,
∴∠B=∠ACD,
5.已知:如图,△ABC中,∠ACB=90°,CD⊥AB于D,AB=8,BC=3.求:sin∠ACD的值及AD的长.
变式练习
【点评】本题考查解直角三角形,锐角三角函数等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
【解答】解:设BC=x.
∵∠DBC=45°,EF⊥AE,
∴EF=BE,BC=DC,
∴AC=2+x,
6.如图,在△ADC中,∠A=30°,∠ACD=90°,点B在AC上,∠DBC=45°,点E在BC的延长线上,且AB=2,CE=3,过E作EF⊥AE于E,交BD延长线于F.求EF的长.
教学反思:
用特殊值探究锐角的三角函数时,学生们表现得非常积极,从作图,找边、角,计算各个方面进行探究,学生发现:特殊角的三角函数值可以用勾股定理求出,然后就问:三角函数与直角三角形的边、角有什么关系,三角函数与三角形的形状有关系吗 进一步深入地去认识三角函数:当得出正切的概念后,学生们就提出:能不能把公式变形成积的形式,去求边,这个问题已经把本课的内容拓展了,说明学生的问题意识已经增强了,能够合理地提出问题。至此,每个学生在课堂的表现明显改变,表现得积极、主动、问题意识强。
你理解了正弦,余弦正切的涵义了吗?
课后作业:
D
A
D
课后作业:
4.如图,△ABC中,∠C=90°,BC=2,AB=3,则下列结论正确的是( )
5.将∠BAC放置在5×5的正方形网格中,顶点A在格点上.则sin∠BAC的值为 .
D
课后作业:
【解答】解:(1)作AE⊥BC于E,如图,
∵AB=AC,
(2)作DF⊥BC于F,如图
设DF=3x,则CF=5x,
课后作业:
【点评】本题考查了解直角三角形:灵活运用锐角三角形的定义和勾股定理解直角三角形.也考查了等腰三角形的性质.
而DF=3x,
∴BF=4x,
∴BC=BF+CF=4x+5x=9x,
8.在Rt△ABC中,∠C=90°,斜边c=5,两直角边的长a,b是关于x的一元二次方程x2﹣mx+2m﹣2=0的两个根,求Rt△ABC中较小锐角的正弦值.
课后作业:
【点评】本题难度较大,利用了一元二次方程的根与系数的关系,勾股定理,正弦的概念求解.
【解答】解:∵a,b是方程x2﹣mx+2m﹣2=0的解,
∴a+b=m,ab=2m﹣2,
在Rt△ABC中,由勾股定理得,a2+b2=c2,
而a2+b2=(a+b)2﹣2ab,c=5
∴a2+b2=(a+b)2﹣2ab=25,
即:m2﹣2(2m﹣2)=25
解得,m1=7,m2=﹣3,
∵a,b是Rt△ABC的两条直角边的长.
∴a+b=m>0,m=﹣3不合题意,舍去.
∴m=7,
当m=7时,原方程为x2﹣7x+12=0,
解得,x1=3,x2=4,
课后作业:
【点评】本题考查的是解直角三角形的知识,正确作出辅助线构造直角三角形是解题的关键,注意锐角三角函数的概念的正确应用.
【解答】解:(1)过点A作AE⊥BC于点E,
∴∠C=45°,
在Rt△ACE中,CE=AC cosC=1,
∴AE=CE=1,
∴BE=3AE=3,
∴BC=BE+CE=4;
(2)∵AD是△ABC的中线,
∴DE=CD﹣CE=1,
∵AE⊥BC,DE=AE,
∴∠ADC=45°.
一、教学目标
知识技能目标:1.了解三角函数的概念,学会在直角三角形中进行一些简单的计算。
2.知道30°、45°、60°角的三角函数值;会使用计算器由已知锐角求它的三角函数值, 由已知三角函数值求它对应的锐角。
3.理解并掌握直角三角形边角之间的关系
过程方法目标:
(1)通过体验三角函数概念的形成过程增进学生的数学经验
(2)渗透数形结合的数学思想方法
(3)培养学生主动探索,敢于实践,勇于发现,合作交流的精神。
情感态度目标:
(1)让学生感受数学来源于生活又应用于生活,体验数学的生活化经历。
(2)通过实际问题情境的经历探究性的学习培养学生学习数学的兴趣,培养学生热爱数学、热爱生活的情感。
二、教学重点:
锐角三角函数的概念及其简单的计算
三、教学难点:
三角函数概念的形成
操场里有一个旗杆,老师让小明去测量旗杆高度,小明站在离旗杆底部10米远处,目测旗杆的顶部,视线与水平线的夹角为34度,并已知目高为1.65米.然后他很快就算出旗杆的高度了。
1.65米
10米
你想知道小明怎样算出的吗?
引例
∠A的对边 a
∠A的邻边 b
直角三角形ABC可以简记为Rt△ABC
直角∠C所对的边AB称为斜边,用c表示
另两条直角边分别叫∠A的对边与邻边,用a、b表示.
A
B
C
斜边 C
Rt△OPM∽Rt△OP1M1
P1M1
OP1
PM
OP
所以
OM
OP
OM1
OP1
PM
OM
OM
PM
P1M1
OM1
=______,
=______,
=______,
OM1
P1M1
=______,
B
A
M1
M
O
P
P1
图中的Rt△OPM和Rt△OP1M1,它们之间有什么关系?
在Rt△ABC中,对于锐角A的每一个确定的值,
①∠A的对边与斜边的比值与△ABC的边长大小有关系吗?
②∠A的邻边与斜边的比值呢?
③∠A的对边与邻边的比值呢?
在Rt△ABC中,对于锐角A的每一个确定的值,其对边与斜边、邻边与斜边、对边与邻边的比值是惟一确定的.
由此可见
这几个比值都是锐角∠A的函数,记作sin A、cosA、tan A,即
sin A=
cosA=
tan A=
分别叫做锐角∠A的正弦、余弦、正切,统称为锐角∠A的三角函数.
方法指导:
(1)我们现阶段所研究的锐角三角函数都是在直角三角形中定义的;
(2) sinA ,cosA、 tanA 都是表达符号,它们是一个整体,不能拆开来理解:
(3) sinA , cosA、 tanA 中 ∠A 的角的记号“ ∠ ”习惯上省略不写 ,但对于用三个字母和阿拉伯数字表示的角,角的记号“∠”不能省略,例如 sin∠1不能写成 sin1 .
0﹤ sin A﹤1, 0﹤ cos A﹤1 为什么
根据三角函数定义,我们还可以得出
你能够证明这两个公式吗?试试看
显然
求出如图所示的Rt△ABC中∠A的三角函数值.
∵
∴ sinA =
cosA =
tanA =
解
例 1
变式练习:
1.下图中∠ACB=90° ,CD⊥AB
指出∠A的对边、邻边。
A
B
C
D
2.上题中如果CD=5,AC=10,
则sin∠ACD=________
sin ∠DCB=________
3(1)在△ABC中,∠B=90 ,BC=3,AB=4,
则tanA=_____ cosA=______
(2)tan20 ·tan(90 -∠A)=1,则锐角∠A=_____
例 2
【点评】本题主要考查了三角函数的定义,正确求出图形中的线段的长是解决本题的关键.
因而可以设CD=3x,AD=5x,
根据勾股定理得到AC=4x,则BC=AD=5x,
∵BD=4,∴5x﹣3x=4,
解得x=2,
因而BC=10,AC=8,
CD=6;
如图,在△ABC中∠C=90°,点D在BC上,BD=4,AD=BC,
求:(1)DC的长;(2)sinB的值.
变式练习:
∴AC=4,
∴BC=CD+DB=3+5=8,
4.如图,在Rt△ABC中,∠C=90°,点D在边BC上,AD=BD=5,
【点评】本题考查了直角三角形中正弦值的计算,考查了勾股定理的运用,本题中求AC的长是解题的关键.
变式练习
【解答】解:∵CD⊥AB,∠ACB=90°,
∴∠B=∠ACD,
5.已知:如图,△ABC中,∠ACB=90°,CD⊥AB于D,AB=8,BC=3.求:sin∠ACD的值及AD的长.
变式练习
【点评】本题考查解直角三角形,锐角三角函数等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
【解答】解:设BC=x.
∵∠DBC=45°,EF⊥AE,
∴EF=BE,BC=DC,
∴AC=2+x,
6.如图,在△ADC中,∠A=30°,∠ACD=90°,点B在AC上,∠DBC=45°,点E在BC的延长线上,且AB=2,CE=3,过E作EF⊥AE于E,交BD延长线于F.求EF的长.
教学反思:
用特殊值探究锐角的三角函数时,学生们表现得非常积极,从作图,找边、角,计算各个方面进行探究,学生发现:特殊角的三角函数值可以用勾股定理求出,然后就问:三角函数与直角三角形的边、角有什么关系,三角函数与三角形的形状有关系吗 进一步深入地去认识三角函数:当得出正切的概念后,学生们就提出:能不能把公式变形成积的形式,去求边,这个问题已经把本课的内容拓展了,说明学生的问题意识已经增强了,能够合理地提出问题。至此,每个学生在课堂的表现明显改变,表现得积极、主动、问题意识强。
你理解了正弦,余弦正切的涵义了吗?
课后作业:
D
A
D
课后作业:
4.如图,△ABC中,∠C=90°,BC=2,AB=3,则下列结论正确的是( )
5.将∠BAC放置在5×5的正方形网格中,顶点A在格点上.则sin∠BAC的值为 .
D
课后作业:
【解答】解:(1)作AE⊥BC于E,如图,
∵AB=AC,
(2)作DF⊥BC于F,如图
设DF=3x,则CF=5x,
课后作业:
【点评】本题考查了解直角三角形:灵活运用锐角三角形的定义和勾股定理解直角三角形.也考查了等腰三角形的性质.
而DF=3x,
∴BF=4x,
∴BC=BF+CF=4x+5x=9x,
8.在Rt△ABC中,∠C=90°,斜边c=5,两直角边的长a,b是关于x的一元二次方程x2﹣mx+2m﹣2=0的两个根,求Rt△ABC中较小锐角的正弦值.
课后作业:
【点评】本题难度较大,利用了一元二次方程的根与系数的关系,勾股定理,正弦的概念求解.
【解答】解:∵a,b是方程x2﹣mx+2m﹣2=0的解,
∴a+b=m,ab=2m﹣2,
在Rt△ABC中,由勾股定理得,a2+b2=c2,
而a2+b2=(a+b)2﹣2ab,c=5
∴a2+b2=(a+b)2﹣2ab=25,
即:m2﹣2(2m﹣2)=25
解得,m1=7,m2=﹣3,
∵a,b是Rt△ABC的两条直角边的长.
∴a+b=m>0,m=﹣3不合题意,舍去.
∴m=7,
当m=7时,原方程为x2﹣7x+12=0,
解得,x1=3,x2=4,
课后作业:
【点评】本题考查的是解直角三角形的知识,正确作出辅助线构造直角三角形是解题的关键,注意锐角三角函数的概念的正确应用.
【解答】解:(1)过点A作AE⊥BC于点E,
∴∠C=45°,
在Rt△ACE中,CE=AC cosC=1,
∴AE=CE=1,
∴BE=3AE=3,
∴BC=BE+CE=4;
(2)∵AD是△ABC的中线,
∴DE=CD﹣CE=1,
∵AE⊥BC,DE=AE,
∴∠ADC=45°.
