北师大版2021-2022学年八年级数学上册3.3轴对称与坐标变化课件(共25张PPT)
文档属性
| 名称 | 北师大版2021-2022学年八年级数学上册3.3轴对称与坐标变化课件(共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 571.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-28 21:10:25 | ||
图片预览








文档简介
(共25张PPT)
3.3 轴对称与坐标变化
八年级上册
学习目标
1.根据已知条件.按要求画图、找出图中变换的坐标.
2.感受在同一坐标系中图形中点的坐标变化与图形变化之间的关系.
3.学会形象思维能力、培养数形结合的意识,并用来分析、解决问题.
学习重难点
重点
难点
明确图形坐标变化与图形轴对称之间关系.
由坐标的变化探索新旧图形之间的变化探索过程,发展形象思维能力和数形结合意识.
如右图所示的平面直角坐标系中,
第一、二象限内各有一面小旗.
观察
(1)两面小旗之间有怎样的位置关系?
关于y轴成轴对称
对应点 的坐标又有什么特点?
纵坐标相等,横坐标互为相反数
其他对应的点也有这个特点吗?
同样具有
(2,6)
(-2,6)
如右图所示的平面直角坐标系中,
第一、二象限内各有一面小旗.
观察
(2)在这个坐标系里画出小旗ABCD关于x轴的对称图形,它的各个“顶点”的坐标与原来的点的坐标有什么关系?
横坐标相等,纵坐标互为相反数
(2,6)
(2,-6)
关于x轴对称的两点的坐标, 相同, 互为相反数
关于y轴对称的两点的坐标, 互为相反数, 相同
横坐标
纵坐标
横坐标
纵坐标
要点
(1)点P关于x轴对称的点的坐标是 ;
1.已知点P(-3,4),则
(2)点P关于y轴对称的点的坐标是 ;
(-3,-4)
(3,4)
2.已知点P(a,b),则
(1)点P关于x轴对称的点的坐标是 ;
(2)点P关于y轴对称的点的坐标是 ;
(a,-b)
(-a,b)
注意:关于什么轴对称,什么坐标不变,另一坐标变为原来的相反数
练一练
1
2
3
4
5
-1
-2
-3
0
–1
–2
–3
–4
–5
1
2
3
4
-4
-5
5
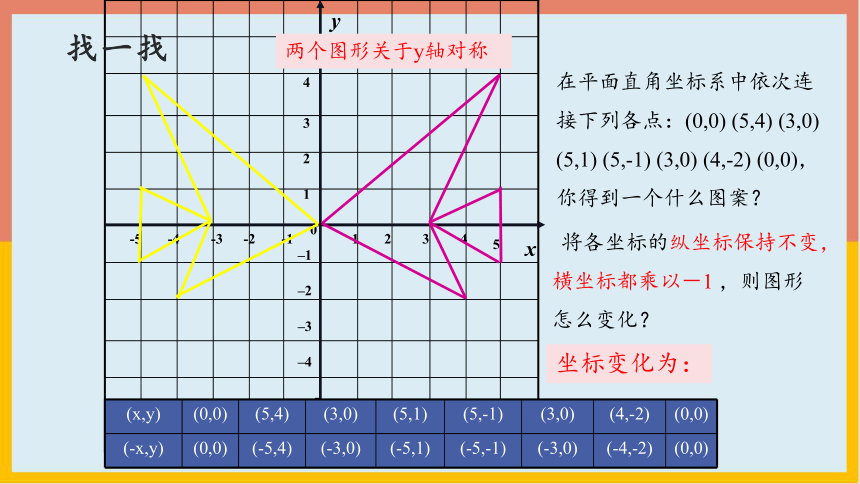
在平面直角坐标系中依次连接下列各点:(0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0),你得到一个什么图案?
y
x
两个图形关于y轴对称
坐标变化为:
(x,y) (0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)
(-x,y) (0,0) (-5,4) (-3,0) (-5,1) (-5,-1) (-3,0) (-4,-2) (0,0)
将各坐标的纵坐标保持不变,横坐标都乘以-1 ,则图形怎么变化?
找一找
特征
(x , y)
(-x , y)
横坐标互为相反数,纵坐标相同
1.关于y轴对称的两个图形上点的坐标特征:
1
2
3
4
5
6
7
8
0
–1
–2
–3
–4
–5
1
2
3
4
5
图中的鱼是将坐标为:(0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)的点用线段依次连接而成的
将各坐标的纵坐标都乘以-1,横坐标保持不变,则图形怎么变化?
坐标变化为:
y
x
与原图形关于x轴对称
(x,y) (0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)
(x,-y) (0,0) (5,-4) (3,0) (5,-1) (5, 1) (3,0) (4, 2) (0,0)
找一找
特征
(x , y)
(-x , y)
2.关于x轴对称的两个图形上点的坐标特征:
(x , y)
(x , -y)
横坐标互为相反数,纵坐标相同
横坐标相同,纵坐标互为相反数
1.关于y轴对称的两个图形上点的坐标特征:
图形的点的坐标变化与图形的变化有怎样的关系?
1.横坐标保持不变,纵坐标互为相反数,所得图形与原图形关于 ________成轴对称.
2.纵坐标保持不变,横坐标互为相反数,所得图形与原图形关于 ______成轴对称.
x轴
y轴
议一议
A
1. 在直角坐标系中,点A(1,2)的纵坐标乘以-1,横坐标不变,得到点B,则点A与点B的关系是( )
A. 关于x轴对称 B. 关于y轴对称
C. 关于x轴、y轴均不对称 D. 不确定
2. 如果点A(1-a, b+1)关于y轴的对称点在第三象限,那么点B(1-a, b)在( )
A. 第一象限 B. 第二象限
C. 第三象限 D. 第四象限
D
针对训练
1. 将平面直角坐标系内某个图形各点的横坐标都乘以-1,纵坐标不变,所得图形与原图形的关系是( )
A. 关于x轴对称 B. 关于y轴对称
C. 两图形重合 D. 不确定
B
2. 已知△ABC在直角坐标系中的位置如图所示,如果△A′B′C′与△ABC关于y轴对称,那么点A的对应点A′的坐标为( )
A. (4,4) B. (-4,4)
C. (4,-4) D. (-4,-4)
A
课堂练习
3.点M(x,y)在第二象限内,且|x|=2,|y|=3,则点M关于x轴的对称点的坐标是( )
A. (2,3) B. (-2,-3)
C. (-3,2) D. (-3,-2)
B
课堂练习
4. 线段MN在直角坐标系中的位置如图所示,若线段M′N′与MN关于y轴对称,则点M的对应点M′的坐标为( )
A. (4,2) B. (-4,2)
C. (-4,-2) D. (4,-2)
D
6.已知点A(x1,-5),B(2,y2),若:
(1)点A,B关于x轴对称,则x1=_______,y2=________;
(2)点A,B关于y轴对称,则x1= ______,y2=________.
-2
2
5
-5
课堂练习
5.已知点P1(a,-3)和点P2(3,b)关于y轴对称,则a+b的值为______.
-6
7.如图,已知△ABC的三个顶点的坐标都在格点上,分别为A(-2,3),B(-6,0),C(-1,0).
(1)请将点A,B,C的纵坐标分别乘以-1后得到点A′,B′,C′描在坐标系中,并顺次连接A′,B′,C′得到△A′B′C′;
(2)请问△A′B′C′与△ABC有怎样的位置关系?
课堂练习
解:(1)所作图形如图所示.
(2)由图可得,△A′B′C′与△ABC关于x轴对称.
课堂练习
8.在平面直角坐标系中,已知点A(-2,-3)关于x轴对称的点为B点,关于y轴对称的点为C点,求△ABC的面积.
解:如图,因为点A(-2,-3)关于x轴对称的点为B点,关于y轴对称的点为C点,所以B(-2,3),C(2,-3).
所以S△ABC= ×AB×AC= ×6×4=12.
课堂练习
9.如图,正方形ABCD关于x轴,y轴均成轴对称,若这个正方形的面积为16,请分别写出点A,B,C,D的坐标.
解:设正方形的边长为a,则a2=16.
解得a=4或a=-4(不符合题意,舍去).
所以A(2,2),B(-2,2),
C(-2,-2),D(2,-2).
课堂练习
10.在棋盘中建立如图所示的坐标系,三颗棋子A,O,B的位置如图1,它们的坐标分别是(-1,1),(0,0),(1,0).
(1)如图2,添加棋子C,使四颗棋子A,O,B,C成为一个轴对称图形,请在图中画出该图形的对称轴;
(2)在其他格点位置添加一颗棋子P,使四颗棋子A,O,B,P成为轴对称图形,请直接写出棋子P的坐标(写出2个即可).
课堂练习
解:(1)如图3;
(2)如图4,P的坐标为(-1,-1)或(2,1).
图3
图4
课堂练习
总结
1、关于y轴对称的两个图形上点的坐标特征:
(x , y)
(-x , y)
2、关于x轴对称的两个图形上点的坐标特征:
(x , y)
(x , -y)
课后作业
1.若某四边形顶点的横坐标变为原来的相反数,而纵坐标不变,此时图形位置也不变,则这个四边形不是( )
A.矩形 B.直角梯形 C.正方形 D.菱形
2.在平面直角坐标系中,直线l过点M(3,0),且平行于y轴。
(1)如果△ABC三个顶点的坐标分别是A(-2,0),B(-1,0),C(-1,2),△ABC关于y轴的对称图形是△A1B1C1, △A1B1C1关于直线l的对称图形是△A2B2C2,写出△ A2B2C2的三个顶点的坐标;
(2)如果点P的坐标是(-a,0),其中a>0,点P关于y轴的对称点是P1,点P1关于直线的对称点是P2,求PP2的长。
再 见
3.3 轴对称与坐标变化
八年级上册
学习目标
1.根据已知条件.按要求画图、找出图中变换的坐标.
2.感受在同一坐标系中图形中点的坐标变化与图形变化之间的关系.
3.学会形象思维能力、培养数形结合的意识,并用来分析、解决问题.
学习重难点
重点
难点
明确图形坐标变化与图形轴对称之间关系.
由坐标的变化探索新旧图形之间的变化探索过程,发展形象思维能力和数形结合意识.
如右图所示的平面直角坐标系中,
第一、二象限内各有一面小旗.
观察
(1)两面小旗之间有怎样的位置关系?
关于y轴成轴对称
对应点 的坐标又有什么特点?
纵坐标相等,横坐标互为相反数
其他对应的点也有这个特点吗?
同样具有
(2,6)
(-2,6)
如右图所示的平面直角坐标系中,
第一、二象限内各有一面小旗.
观察
(2)在这个坐标系里画出小旗ABCD关于x轴的对称图形,它的各个“顶点”的坐标与原来的点的坐标有什么关系?
横坐标相等,纵坐标互为相反数
(2,6)
(2,-6)
关于x轴对称的两点的坐标, 相同, 互为相反数
关于y轴对称的两点的坐标, 互为相反数, 相同
横坐标
纵坐标
横坐标
纵坐标
要点
(1)点P关于x轴对称的点的坐标是 ;
1.已知点P(-3,4),则
(2)点P关于y轴对称的点的坐标是 ;
(-3,-4)
(3,4)
2.已知点P(a,b),则
(1)点P关于x轴对称的点的坐标是 ;
(2)点P关于y轴对称的点的坐标是 ;
(a,-b)
(-a,b)
注意:关于什么轴对称,什么坐标不变,另一坐标变为原来的相反数
练一练
1
2
3
4
5
-1
-2
-3
0
–1
–2
–3
–4
–5
1
2
3
4
-4
-5
5
在平面直角坐标系中依次连接下列各点:(0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0),你得到一个什么图案?
y
x
两个图形关于y轴对称
坐标变化为:
(x,y) (0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)
(-x,y) (0,0) (-5,4) (-3,0) (-5,1) (-5,-1) (-3,0) (-4,-2) (0,0)
将各坐标的纵坐标保持不变,横坐标都乘以-1 ,则图形怎么变化?
找一找
特征
(x , y)
(-x , y)
横坐标互为相反数,纵坐标相同
1.关于y轴对称的两个图形上点的坐标特征:
1
2
3
4
5
6
7
8
0
–1
–2
–3
–4
–5
1
2
3
4
5
图中的鱼是将坐标为:(0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)的点用线段依次连接而成的
将各坐标的纵坐标都乘以-1,横坐标保持不变,则图形怎么变化?
坐标变化为:
y
x
与原图形关于x轴对称
(x,y) (0,0) (5,4) (3,0) (5,1) (5,-1) (3,0) (4,-2) (0,0)
(x,-y) (0,0) (5,-4) (3,0) (5,-1) (5, 1) (3,0) (4, 2) (0,0)
找一找
特征
(x , y)
(-x , y)
2.关于x轴对称的两个图形上点的坐标特征:
(x , y)
(x , -y)
横坐标互为相反数,纵坐标相同
横坐标相同,纵坐标互为相反数
1.关于y轴对称的两个图形上点的坐标特征:
图形的点的坐标变化与图形的变化有怎样的关系?
1.横坐标保持不变,纵坐标互为相反数,所得图形与原图形关于 ________成轴对称.
2.纵坐标保持不变,横坐标互为相反数,所得图形与原图形关于 ______成轴对称.
x轴
y轴
议一议
A
1. 在直角坐标系中,点A(1,2)的纵坐标乘以-1,横坐标不变,得到点B,则点A与点B的关系是( )
A. 关于x轴对称 B. 关于y轴对称
C. 关于x轴、y轴均不对称 D. 不确定
2. 如果点A(1-a, b+1)关于y轴的对称点在第三象限,那么点B(1-a, b)在( )
A. 第一象限 B. 第二象限
C. 第三象限 D. 第四象限
D
针对训练
1. 将平面直角坐标系内某个图形各点的横坐标都乘以-1,纵坐标不变,所得图形与原图形的关系是( )
A. 关于x轴对称 B. 关于y轴对称
C. 两图形重合 D. 不确定
B
2. 已知△ABC在直角坐标系中的位置如图所示,如果△A′B′C′与△ABC关于y轴对称,那么点A的对应点A′的坐标为( )
A. (4,4) B. (-4,4)
C. (4,-4) D. (-4,-4)
A
课堂练习
3.点M(x,y)在第二象限内,且|x|=2,|y|=3,则点M关于x轴的对称点的坐标是( )
A. (2,3) B. (-2,-3)
C. (-3,2) D. (-3,-2)
B
课堂练习
4. 线段MN在直角坐标系中的位置如图所示,若线段M′N′与MN关于y轴对称,则点M的对应点M′的坐标为( )
A. (4,2) B. (-4,2)
C. (-4,-2) D. (4,-2)
D
6.已知点A(x1,-5),B(2,y2),若:
(1)点A,B关于x轴对称,则x1=_______,y2=________;
(2)点A,B关于y轴对称,则x1= ______,y2=________.
-2
2
5
-5
课堂练习
5.已知点P1(a,-3)和点P2(3,b)关于y轴对称,则a+b的值为______.
-6
7.如图,已知△ABC的三个顶点的坐标都在格点上,分别为A(-2,3),B(-6,0),C(-1,0).
(1)请将点A,B,C的纵坐标分别乘以-1后得到点A′,B′,C′描在坐标系中,并顺次连接A′,B′,C′得到△A′B′C′;
(2)请问△A′B′C′与△ABC有怎样的位置关系?
课堂练习
解:(1)所作图形如图所示.
(2)由图可得,△A′B′C′与△ABC关于x轴对称.
课堂练习
8.在平面直角坐标系中,已知点A(-2,-3)关于x轴对称的点为B点,关于y轴对称的点为C点,求△ABC的面积.
解:如图,因为点A(-2,-3)关于x轴对称的点为B点,关于y轴对称的点为C点,所以B(-2,3),C(2,-3).
所以S△ABC= ×AB×AC= ×6×4=12.
课堂练习
9.如图,正方形ABCD关于x轴,y轴均成轴对称,若这个正方形的面积为16,请分别写出点A,B,C,D的坐标.
解:设正方形的边长为a,则a2=16.
解得a=4或a=-4(不符合题意,舍去).
所以A(2,2),B(-2,2),
C(-2,-2),D(2,-2).
课堂练习
10.在棋盘中建立如图所示的坐标系,三颗棋子A,O,B的位置如图1,它们的坐标分别是(-1,1),(0,0),(1,0).
(1)如图2,添加棋子C,使四颗棋子A,O,B,C成为一个轴对称图形,请在图中画出该图形的对称轴;
(2)在其他格点位置添加一颗棋子P,使四颗棋子A,O,B,P成为轴对称图形,请直接写出棋子P的坐标(写出2个即可).
课堂练习
解:(1)如图3;
(2)如图4,P的坐标为(-1,-1)或(2,1).
图3
图4
课堂练习
总结
1、关于y轴对称的两个图形上点的坐标特征:
(x , y)
(-x , y)
2、关于x轴对称的两个图形上点的坐标特征:
(x , y)
(x , -y)
课后作业
1.若某四边形顶点的横坐标变为原来的相反数,而纵坐标不变,此时图形位置也不变,则这个四边形不是( )
A.矩形 B.直角梯形 C.正方形 D.菱形
2.在平面直角坐标系中,直线l过点M(3,0),且平行于y轴。
(1)如果△ABC三个顶点的坐标分别是A(-2,0),B(-1,0),C(-1,2),△ABC关于y轴的对称图形是△A1B1C1, △A1B1C1关于直线l的对称图形是△A2B2C2,写出△ A2B2C2的三个顶点的坐标;
(2)如果点P的坐标是(-a,0),其中a>0,点P关于y轴的对称点是P1,点P1关于直线的对称点是P2,求PP2的长。
再 见
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
